Кинетика испарения металлов из Sb-Pb-Ag сплава при вакуумной перегонке

Вакуумная перегонка считается одним из самых эффективных и экологически чистых методов для разделения и очистки, переработки и рафинирования различных металлов. Она имеет ряд преимуществ, таких как относительно низкое потребление энергии, короткий производственный цикл, высокую рентабельность, отсутствие подлежащих утилизации отходов, по сравнению с традиционными методами, например, пирометаллургической переработкой и электролизом [1–4]. Возмож- ности разделения черновых металлов путем расчета точки кипения и давления пара чистых компонентов-примесей и коэффициента разделения полиметаллических сплавов при различных экспериментальных условиях были изучены ранее [5–8]. Результаты исследования показали содержание сурьмы и свинца менее 0,01 % в рафинированном серебре при вакуумной перегонке. В предыдущих работах были получены диаграмма равновесного состава «газ – жидкость» и диаграмма равновесных фаз «газ–жидкость» [9–11].

В настоящее время большинство исследований сконцентрировано в основном на термодинамике разделения полиметаллических сплавов вакуумной перегонкой, поскольку позволяет определить возможность, направление и ограничение протекания металлургических реакций [12]. При изучении кинетики испарения металлов можно выявить эффективные условия процесса, такие как температура, степень вакуума и продолжительность перегонки, необходимые при проектировании процесса разделения компонентов сплавов. Целью работы являлось определение скорости испарения металлов из Sb–Pb–Ag сплавов различного состава в зависимости от температуры и давления, а также выявление лимитирующей стадии процесса.

рость испарения металла можно записать сле-

дующим образом:

–

dw(t) S dt " К Me

p

n –1

V 100 М ме J

w ( t ) n .       ⁽⁴⁾

Для реакций первого порядка ( n = 1)

справедливо равенство

( S

In W (t ) = ln W (o) ^- k _Me I vt

В данном исследовании из трех стадий испарения процессом (в) можно пренебречь при рабочем давлении в системе ( р ≤ 13,3 Па),

которое ниже критического давления для легко возгоняемых cурьмы (273,7 Па) и свинца (27,5 Па) [14], поэтому общая скорость реак-

Испарение металла из жидкой в газовую фазу при низком давлении включает в себя следующие стадии: массоперенос в жидкой фазе (а); испарение в поверхностный слой на границе раздела фаз «жидкость – газ» (б); массоперенос в газовой фазе (в) [1]. Уравне-

ции не лимитируется массопереносом в газовой фазе. В результате лимитирующая стадия связана с двумя другими стадиями, обладаю-

щими сопротивлением: массопереносом в жидком металле и через поверхностный слой на границе раздела фаз. В соответствии с

принципами массного переноса, который мы обсуждали выше, константа скорости испарения металла может быть выражена как

ние скорости испарения в процессе перегонки [13]:

dd^ = - V к ме С ( t ) n ;                 (1)

V = ml p ;                              (2)

^kMe =

( 1

IL

V ^kMe

\—1

V V ^kMe J

,

где k _M ^L _e и k _M ^V _e – коэффициенты массоперено-са металла (м·с^–1) в жидкой и газовой фазах,

P =

w Sb + ^w Pb + w Ag

- 1

V^p Sb    ^p Pb    ^p Ag J

соответственно.

Скорость испарения компонентов сплава представлена формулой (7), производной от

где с – концентрация испаряющегося элемента в расплаве в момент времени t ; k_Me – константа скорости испарения; S и V – площадь поверхности и объем расплава, соответственно. Значение V можно вычислить через плотность (ρ) и массу ( m ) сплава по уравнению (2); w Sb , w Pb и w Sn – массные доли Sb, Pb и Sn в жидкой фазе; n – порядок реакции. Разные порядки реакции для металлов соответствуют различным формам расчетных уравнений. Существует три способа для определения порядка реакции: метод интеграции, метод половинного изменения и графический метод. Графический метод обычно используется для проверки порядка реакции.

Если мы используем массовую долю для определения концентрации испаряющегося элемента в кинетическом уравнении (1), ско-

выражения для испарения чистого жидкого металла в идеальном вакууме (уравнение Герца – Кнудсена – Ленгмюра) [15]:

*

V = ^aY Me x Me P Me ^Me" 2 n RTM Me

,

где α – коэффициент поверхностного испарения (α = 1 для жидких металлов); γ Ме – коэффициент активности металла; М Ме – атомный вес металла; P _М ^* _е – давление насыщенного

пара чистого металла [16].

Если определена константа скорости испарения k_Me , можно оценить кажущуюся энергию активации по уравнению Аррениуса [15]:

ln kMe =

E ^Me- + C

RT

где Е Ме – кажущаяся энергия активации испарения металла; R – газовая постоянная; C – константа, которая не зависит от температуры Т .

Образцы сплавов Sb–Pb–Ag для эксперимента массой 50–100 г каждый были подготовлены с использованием чистых сурьмы, свинца и серебра (99,99 мас. %). Навески исходных металлов были проплавлены в индукционной печи в атмосфере аргона высокой чистоты для получения сплавов состава, мол. %: 16–77 Sb; 75–20 Pb; 9–3 Ag.

Лабораторные эксперименты по дистилляции компонентов сплавов проводились в вертикальной вакуумной печи [8]. Степень вакуума в печи на время эксперимента составляла 1,33–133 Па, температура 823–1073 К. Состав образцов возгонов и остатков определяли из предварительно полученных растворов атомно-абсорбционным методом на установке GBC 933АВ Plus. В экспериментах использовали образцы сплавов цилиндрической формы. Сначала образец помещали в цилиндрический тигель ( h = 40 мм, d = 40 мм) из тонкодисперсных зерен графита высокой плотности. Затем тигель переносили в вакуумную печь и нагревали, контролируя температуру. Для предотвращения испарения металлов на стадии плавления образца, процесс осуществляли в атмосфере аргона при нормальном давлении. Разряжение в рабочей камере производили паромасляным диффузионным насосом при достижении необходимой температуры – этот момент считали началом вакуумной перегонки ( t = 0). Затем поддержи-

вали в камере давление и температуру в течение заданного времени эксперимента. По окончании опыта выключали обогреватель, аргон заполнял камеру, давление в которой нормализовалось. Металлы, перешедшие в возгоны, конденсировались на холодной пластине, подключенной к циркуляционной водной системе. При температуре 40 °С, возгоны и остаток вынимали из печи и взвешивали.

Для проверки адекватности расчетных значений содержания компонентов сплавов в жидкой и газовой фазах сравнили их с экспериментальными данными. Для этого были вычислены показания среднего относительного отклонения ( S _i ) и среднего квадратичного отклонения ( S _i ^* ):

100 ⁿ х ( у ) _{i , exp}

Si =±100 Z n i=1

_ *

Si =±

n

—

х ( у ) _{i , cal}

х ( у ) i , exp

·100%; (9)

1 n

± "Z[ х ( У ) i,exp _ n i = 1

—

х ( У ) i , cal ^]

0,5

, (10)

где x ( y ) i , exp и x ( y ) i , cal – экспериментальные и расчетные значения содержания компонента i в жидкой ( х ) и газовой ( у ) фазах, соответственно; n – количество экспериментальных данных.

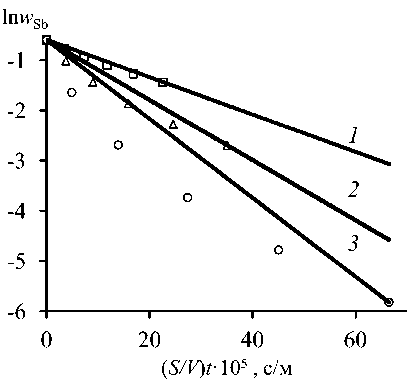
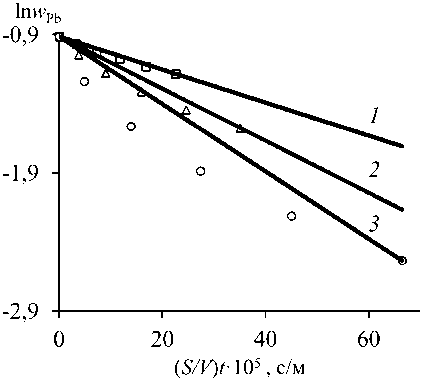
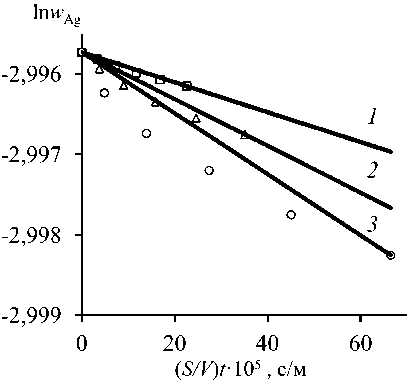
Зависимость ln w ( t ) – ( S/V ) t (табл. 1) описывается линейными функциями (рис. 1). Процесс испарения металлов из Zn–Pb–Ag сплава

Таблица 1

Экспериментальные и расчетные параметры возгонки сплава Sb–Pb–Ag (0,55–0,40–0,05) при давлении 13,3 Па

T , К	t , c	Масса cплава, г	V ·10–7, м 3	w ( t ), % Sb/Pb/Δ w ( t )·105 Ag	( S / V ) t ·105, c/м	ln w ( t ) Sb/Pb/Ag
	0	80,0	97,57	55/40/5	0	–0,598/–0,916/–2,9957
	1200	71,51	76,80	46,49/37,90/0,42	3,366	–0,766/–0,970/–2,9958
823	2400	64,17	60,88	39,30/35,91/0,84	7,276	–0,934/–1,024/–2,9959
	3600	57,80	48,62	33,23/34,02/1,26	11,76	–1,102/–1,078/–2,9960
	4800	52,25	39,12	28,09/32,23/1,68	16,862	–1,270/–1,132/–2,9961
	6000	47,42	31,71	23,74/30,54/2,10	22,599	–1,438/–1,186/–2,9962
	1200	60,95	54,48	36,14/35,05/1,02	3,774	–1,018/–1,048/–2,9959
	2400	47,57	31,88	23,74/30,72/2,04	9,028	–1,438/–1,180/–2,9961
973	3600	38,01	19,57	15,60/26,92/3,06	15,930	–1,858/–1,312/–2,9963
	4800	31,07	12,60	10,25/23,59/4,08	24,594	–2,278/–1,444/–2,9966
	6000	25,92	8,48	6,74/20,67/5,10	35,088	–2,697/–1,576/–2,9968
	1200	42,63	25,11	19,36/28,93/2,52	4,89	–1,642/–1,240/–2,9962
	2400	26,19	8,66	6,82/20,92/5,04	13,94	–2,685/–1,564/–2,9967
1073	3600	18,02	3,84	2,40/15,13/7,55	27,41	–3,730/–1,888/–2,9972
	4800	13,42	2,05	0,84/10,94/10,07	45,05	–4,774/–2,213/–2,9977
	6000	10,56	1,25	0,30/7,92/12,58	66,48	–5,818/–2,536/–2,9983

б)

в)

Рис. 1. Зависимость ln w Me – ( S/V ) t для Sb (а), Pb (b), Ag (c) в сплаве Sb–Pb–Ag (0,55–0,40–0,05) при P = 13,3 Па и T , К: 823 ( 1 ); 973 ( 2 ); 1073 ( 3 )

при данных условиях эксперимента соответствует реакции первого порядка. Линейные зависимости, полученные при использовании метода наименьших квадратов, представлены в табл. 2. Константа испарения металлов k Ме определяется из наклона линейной зависимости ln w ( t ) – ( S/V ) t . Этот показатель также можно рассматривать как коэффициент общего массопереноса. Значения кажущейся константы скорости первого порядка при возгонке металлов из расплава зависят от температуры, давления и химического состава сплава.

При увеличении температуры 823–1073 К ( Р = 13,3 Па; Sb–Pb–Ag (55–40–5)) значения k Ме , м·с^–1, возрастают для сурьмы, свинца и серебра: (3,718–7,852)·10^–7, (1,194–2,436)·10^–7, (1,859–3,790)·10^–10, соответственно.

При понижении давления 133–1,33 Па (Т = 1073 К; Sb–Pb–Ag (55–40–5)) значения kМе, м·с–1, возрастают для сурьмы, свинца и серебра: (5,686–7,473)·10–7, (1,706–2,717)·10–7, (2,843–4,832)·10–10, соответственно.

Зависимость k Ме , м·с^–1, компонентов от доли металлов в сплаве Sb–Pb–Ag носит линейный характер, монотонно возрастая в диапазонах k Sb = (2,881–11,038)·10^–7, k Pb = (1,325– 6,550)·10^–7 и k Ag = (3,458–12,148)·10^–10, при значениях х Sb = 0,16–0,77; х Pb = 0,20–0,75; х Ag = 0,03–0,09.

Линейные зависимости ln K Ме – 1/T, построенные с помощью регрессионного анализа экспериментальных данных, показывают, что влияние температуры на величину коэффициента скорости испарения металлов усиливается от серебра к сурьме (рис. 2).

Величина кажущейся энергии активации испарения ( Е , кДж/моль) металлов получена с помощью уравнения (8): 46,39 Sb; 47,80 Рb; 48,56 Ag (табл. 3).

Таблица 2

Кинетические уравнения возгонки Sb–Pb–Ag сплавов при различных параметрах

T , К	Р , Па	Sb/Pb/Ag	Уравнение	R 2	±Δln w ( t )
823	13,3	55/40/5	ln w Sb = –3,718·10–7( S / V ) t – 0,598 ln w Pb = –1,194·10–7( S / V ) t – 0,916 ln w Ag = –1,859·10–10( S / V ) t – 2,9957	0,997 0,997 0,996	0,0011 0,0012 0,00010
973			ln w Sb = –5,983·10–7( S / V ) t – 0,598 ln w Pb = –1,882·10–7( S / V ) t – 0,916 ln w Ag = –2,906·10–10( S / V ) t – 2,9957	0,988 0,988 0,988	0,0010 0,0013 0,00012
1073			ln w Sb = –7,852·10–7( S / V ) t – 0,598 ln w Pb = –2,436·10–7( S / V ) t – 0,916 ln w Ag = –3,790·10–10( S / V ) t – 2,9957	0,980 0,980 0,984	0,0012 0,0011 0,00011
	133		ln w Sb = –5,686·10–7( S / V ) t – 0,598 ln w Pb = –1,706·10–7( S / V ) t – 0,916 ln w Ag = –2,843·10–10( S / V ) t – 2,9957	0,996 0,996 0,995	0,0013 0,0010 0,00013
	1,33		ln w Sb = –7,473·10–7( S / V ) t – 0,598 ln w Pb = –2,717·10–7( S / V ) t – 0,916 ln w Ag = –4,832·10–10( S / V ) t – 2,9957	0,997 0,997 0,996	0,0012 0,0011 0,00012
	13,3	16/75/9	ln w Sb = –2,881·10–7( S / V ) t – 1,833 ln w Pb = –6,550·10–7( S / V ) t – 0,288 ln w Ag = –12,148·10–10( S / V ) t –2,408	0,998 0,998 0,995	0,0012 0,0013 0,00012
		36/57/7	ln w Sb = –5,278·10–7( S / V ) t – 1,022 ln w Pb = –4,069·10–7( S / V ) t – 0,562 ln w Ag = –7,775·10–10( S / V ) t – 2,6593	0,997 0,997 0,996	0,0011 0,0012 0,00013
		77/20/3	ln w Sb = –11,038·10–7( S / V ) t – 0,261 ln w Pb = –1,325·10–7( S / V ) t – 1,609 ln w Ag = –3,458·10–10( S / V ) t – 3,5066	0,989 0,989 0,986	0,0014 0,0014 0,00015

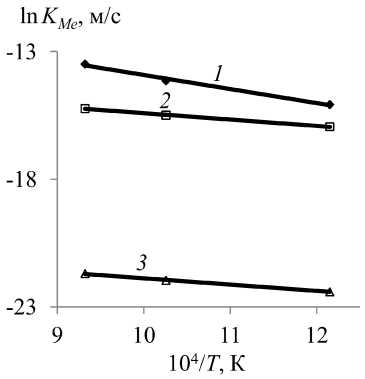
Рис. 2. Зависимость ln K_Ме –1/ T для сурьмы ( 1 ), свинца ( 2 ), cеребра ( 3 ) в сплаве Sb–Pb–Ag (0,55–0,40–0,05) при давлении 13,3 Па

Уровень Е Ме в условиях данного эксперимента значительно ниже, чем значение энергии активации при испарении чистых компонентов сплава, кДж/моль: 160 Sb; 150 Рb; 280 Ag, в температурном диапазоне 823–1073 К и при давлении 13,3 Па [14, 17]. Это означает, что возгонка растворенных компонентов сплава играет важную роль в ограничении общей скорости реакции испарения.

Для точного расчета скорости испарения, как правило, необходимо учитывать неидеальные условия в системе. Уравнение Вильсона базируется на концепции локального состава, который обеспечивает адекватное представление о неидеальных смесях [18]. В данном исследовании рассчитанные коэффициенты активности (γ) по уравнению Вильсона для Sb–Pb–Ag системы представлены в табл. 3.

Таблица 3

Кинетические константы k (м/с) и энергия активации Е (кДж/моль) Sb–Pb–Ag сплавов

T, К Р, Па Sb/Pb/Ag γSb/Pb/Ag kSb/Pb/Ag V kSb/Pb/Ag kSLb/Pb/Ag ESb/Pb/Ag 823 13,3 55/40/5 1,0 0,998 0,923 3,718·10–7 1,194·10–7 1,859·10–10 9,508·10–4 3,517·10–8 1,138·10–13 3,719·10–7 –4,986·10–8 –1,14·10–13 46,41 20,95 20,93 973 1,0 0,998 0,922 5,983·10–7 1,882·10–7 2,906·10–10 0,014 2,166·10–6 4,517·10–11 5,983·10–7 2,061·10–7 –5,35·10–11 1073 1,0 0,999 0,921 7,852·10–7 2,436·10–7 3,790·10–10 0,058 1,751·10–5 9,468·10–10 7,852·10–7 2,470·10–7 6,320·10–10 133 5,686·10–7 1,706·10–7 2,843·10–10 0,058 1,751·10–5 9,468·10–10 5,686·10–7 1,723·10–7 4,063·10–10 – 1,33 7,473·10–7 2,717·10–7 4,832·10–10 0,058 1,751·10–5 9,468·10–10 7,473·10–7 2,760·10–7 9,868·10–10 13,3 16/75/9 1,0 0,999 0,918 2,881·10–7 6,550·10–7 12,148·10–10 0,017 3,283·10–5 1,699·10–9 2,881·10–7 6,683·10–7 1,434·10–9 36/57/7 1,0 0,999 0,920 5,278·10–7 4,069·10–7 7,775·10–10 0,038 2,495·10–5 1,324·10–9 5,278·10–7 4,136·10–7 1,884·10–9 77/20/3 1,0 0,998 0,923 11,038·10–7 1,325·10–7 3,458·10–10 0,081 8,746·10–6 5,693·10–10 1,104·10–6 1,345·10–7 8,808·10–10 продолжительности процесса описывается полиномами первой степени и выражается линейной функцией, где константу скорости испарения можно определить графическим методом по наклону прямой.

• 3.    Повышение температуры свыше 823 К способствует возрастанию константы скорости испарения k_Ме компонентов Sb–Pb–Ag сплава. Снижение давления в системе менее 133 Па способствует возгонке сурьмы, свинца и серебра.

• 4.    Кажущаяся энергия активации испарения металлов, рассчитанная по уравнению Аррениуса, приводит к заключению о более легком испарении компонентов из состава Sb–Pb–Ag сплава, по сравнению с чистым металлом.

• 5.    При расчете активностей каждого компонента Sb–Pb–Ag сплава система демонст-

• 6.    Сравнение общей константы скорости испарения k Ме с коэффициентами скорости испарения k _М ^V _е и массопереноса в жидкой фазе k _М ^L _е показывает, что скорость испарения легко летучих сурьмы и свинца из расплавов Sb–Pb–Ag в основном определяется массопереносом в жидкой фазе вследствие того, что значение коэффициента переноса уменьшается, а сопротивление массоперено-су возрастает.

рирует значительные отрицательные отклонения от закона Рауля на основе уравнения Вильсона. Это очевидно приводит к снижению энергии активации компонента в сплаве (ε ij ), по сравнению с чистыми металлами (ε ii ), как и взаимодействие между молекулами в жидкой фазе.

KINETICS OF METALS EVAPORATIONFROM SB–PB–AG LIQUID ALLOY IN VACUUM DISTILLATION

A.A. Korolev, А.Korolev@elem.ru,S.A. Krayukhin, S.Krauhin@elem.ru, G.I. Maltsev, mgi@elem.ru

JSC “Uralelektromed”, Verkhnyaya Pyshma, Russian Federation

Most of today's research is mostly concentrated on the thermodynamics of the separation of polymetallic alloys by vacuum distillation, as it allows you to determine whether the direction and limitation of the flow of the metallurgical reactions. While studying the kinetics of evaporation of metals it is possible to identify the effective process conditions, such as temperature, vacuum grade and duration of distillation required in the design process for the separation of the components of the alloys. The goal of the work was to determine the rate of evaporation of the metals from the Sb–Pb–Ag alloys of different composition depending on temperature and pressure, and identify the limiting stage of the process. In the making prototype models, sample source metal was welded in an induction furnace in argon atmosphere of high purity, to obtain the alloy composition, mol. %: 16–77 Sb; 75–20 Pb; Ag 9–3. It this work the kinetics of evaporation of metals from Sb–Pb–Ag alloy in temperature range 823–1073 K and a pressure of 1.33–133 Pа is defined, as described by the first order equation. Values of the apparent rate of the first order constants with the sublimation of metals from the melt depends on temperature, pressure and chemical composition of the alloy. The total mass transfer coefficients of lead, antimony, silver ( k Me , m·^.s^–1) evaporation of Sb–Pb–Ag (0,55–0,40–0,05) of the alloy is (3.718–7.852)·10^–7, (1.194–2.436)·10^–7, (1.859–3.790)·10^–10 at T = 823–1073 K, P = 13.3 Pa, respectively. The calculated apparent activation energy of evaporation of the metals from the Sb–Pb–Ag alloy: E = 20,93–46,41 kJ/mol. The apparent activation energy of evaporation of the metals, calculated by the Arrhenius equation leads to the conclusion of an easier evaporation of components from the composition of the Sb–Pb–Ag alloy compared to pure metal: E = 150–280 kJ/mol.

It is shown that quantitative transport of lead and antimony in the gas phase does not limit the speed in vacuum distillation. The evaporation of the metals from the Sb–Pb–Ag alloy is controlled jointly by mass transfer, mainly in the liquid phase, as well as through the surface layer at the phase interface liquid–gas in the studied experimental conditions. Increasing temperatures above 823 K increases the rate constants of the evaporation k Me components Sb–Pb–Ag alloy. Reducing system pressure less than 133 Pa contributes to the sublimation of antimony, lead and silver.