Кинетика превращений аустенита в высокохромистых сплавах железа при непрерывном охлаждении

Сплавы системы «железо – хром – углерод» с высоким содержанием хрома и углерода применяются в промышленности как штамповые стали и износостойкие чугуны [1–6]. Эти сплавы относятся к ледебуритному классу: при нагреве в них происходит образование аустенита, и структура, состоящая из γ -фазы и карбида (Cr, Fe) 7 C 3 , сохраняется вплоть до температуры солидуса. При быстром охлаждении аустенит претерпевает мартенситное превращение (или сохраняется непревращён-ным, если его мартенситная точка оказывается ниже комнатной температуры), а при охлаждении с меньшими скоростями из него

выделяются вторичные карбиды и он испытывает эвтектоидный распад. В работе [7] было построено теоретическое описание процесса растворения карбидов в аустените, а в работах [8, 9] – процессов выделения вторичных карбидов и эвтектоидного превращения аустенита в этих сплавах в изотермических условиях. В данной работе представлено описание диффузионных превращений аустенита в условиях непрерывного охлаждения.

Изотермическое выделение вторичных карбидов

При анализе кинетики выделения вторичных карбидов в высокохромистых чугунах мы

использовали данные работы [10], где были построены термокинетические диаграммы распада аустенита для 14 сплавов с различным содержанием хрома и углерода. Составы этих сплавов приведены в таблице. Сплавы, исследованные в [10], выплавлялись в 10-килограммовой индукционной печи и разливались при температуре 1400 °C в песчаные формы в отливки диаметром 25 и длиной 250 мм. Термокинетические диаграммы строились дилатометрическим методом после 20-минутной аустенитизации при 1000 °C.

Высокохромистые сплавы, исследованные в [10] High-chromium alloys studied in [10]

Обозначение по [10]	Химический состав*, мас. %		y CКr	ауст f К	T s , °C	7 200 , К 1
	Cr	C
1AX	11,65	2,19	0,5344	0,1802	939	1,6132·10–4
2AX	12,65	2,65	0,4982	0,2337	912	1,4919·10–4
3AX	12,20	3,51	0,3884	0,3292	844	–
1BX	15,85	2,08	0,6488	0,1940	936	1,2430·10–4
2BX	14,95	2,67	0,5507	0,2443	937	1,4120·10–4
3BX	14,45	3,58	0,4334	0,3462	857	–
4BX	15,10	4,10	0,3970	0,4101	830	–
4CX	18,22	4,13	0,4581	0,4227	844	–
1DX	20,55	2,08	0,7392	0,2126	906	7,8163·10–5
2DX	20,75	2,67	0,6727	0,2714	913	9,2917·10–5
3DX	20,35	3,62	0,5533	0,3667	909	–
2EX	25,82	2,95	0,7298	0,3141	885	6,1109·10–5
3EX	25,32	3,70	0,6379	0,3908	894	7,7368·10–5
4EX	24,80	4,31	0,5642	0,4548	895	–

* Все сплавы содержали также 0,7 % Mn; 1 % Si; 0–0,02 % Mo; 0,04 % S; 0,06 % P.

В работе [7] была создана – также на основе данных [10] – модель растворения карбидов в высокохромистых чугунах, позволяющая рассчитать состав аустенита и долю карбидной фазы M7C3 после заданных температуры T и времени t выдержки. Количество карбидной фазы в ходе изотермической выдержки меняется по закону

f к = f Равн + ( f и — Л^РаВн ) • exP

—

pi exp----

¹     ( RT ) ( f исх

К

исх 4 3 ( f_К  )

—

f р^авн ) • (1 — f р^авн )

\V2 "

• t

,

где f равн – равновесная доля карбидной фазы при данной температуре (она может быть найдена из термодинамического расчёта равновесия у+M7C3; мы пользовались при этом термодинамическим описанием системы Fe–Cr–C из работы [11]; методика термодинамических расчётов описана в [12]); fКисх – исходное (при t = 0) количество карбидной фазы; энергия активации процесса растворения зависит от атомной доли хрома в металлической подрешётке карбида yCКr :

Г 258,0 — 116,5 у К при у К <  0,5732;

115,0 +133,0уKr при уKr > 0,5732, кДж/моль, а коэффициент ln р1 = 17,406 — 9,653fK?™, мин-1.

Рассчитанные с помощью соотношения (1) доли карбида после 20-минутной аустенитизации при 1000 °C приведены в таблице.

Для анализа кинетики выделения вторичных карбидов мы использовали данные о повышении мартенситной точки при уменьшении скорости охлаждения вследствие обеднения аустенита хромом и углеродом.

В изотермических условиях процесс выделения вторичных карбидов должен подчиняться уравнению общего вида [7]

f к = f Г + ( f нач - f ) • exP [— ( o D^ ) n ] ,                                             (4)

где D = D exp [—— ⁰ I RT

- коэффициент диффузии (хрома) в у-фазе, коэффициент а зависит от ко личества карбидной фазы (по-разному в зависимости от n), а показатель n определяется характером выделения карбидной фазы. В двух предельных случаях он равен n = 1/2 при «подрастании» очень крупных карбидных частиц и n = 3/2 - при росте вновь зародившихся мелких карбидов.

На рис. 1 схематически показано, как меняется fK в термическом цикле построения изотермической диаграммы. После нагрева до температуры аустенитизации количество карбидов начи- нает уменьшаться от исходного значения fисх до некоторого f^уст, которое меньше равновесно- равн го значения f(ауст.) и зависит от времени выдержки. После этого сплав переохлаждается до температуры изотермической выдержки и начинается процесс выделения карбидов, то есть увеличения fK от ^нач = fауст до предельного значения fравн, отвечающего термодинамическому равновесию при температуре изотермы.

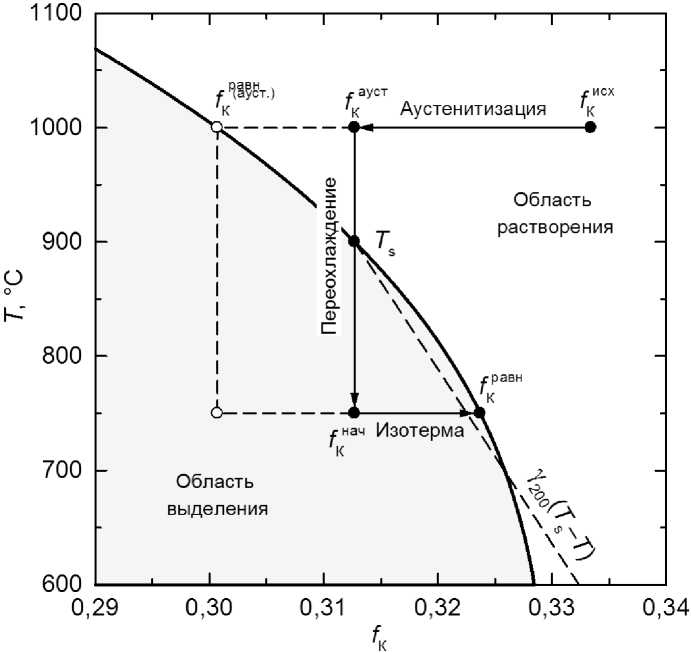
Рис. 1. Схема изменения количества карбидной фазы при аустенитизации, переохлаждении до более низкой изотермы и выдержке при ней (численные значения – для сплава 2EX по [10])

Fig. 1. Scheme of the change in the amount of the carbide phase during austenitization, supercooling to a lower isotherm and holding at it (numerical values are for the 2EX alloy according to [10])

Заметим, что равновесная граница растворимости разделяет поле рис. 1 на две части: если сплав оказывается в области выше неё, где f К >  f равн , то доля карбидной фазы с течением времени будет уменьшаться, приближаясь к f р^авн , то есть будет идти процесс растворения карбидов;

напротив, в области ниже линии равновесной растворимости, где f К <  f равн , доля карбидов будет постепенно увеличиваться, то есть будет происходить их выделение из аустенита. В процессе переохлаждения от температуры аустенитизации до температуры изотермы в какой-то момент сплав пересекает линию равновесия, переходя из области растворения в область выделения. Соответствующая этому моменту температура T _s будет верхней границей выделения карбидов после данного режима аустенитизации, то есть верхней асимптотой С-образной кривой процесса выделения. Эти температуры для всех сплавов после 20-минутной аустенитизации при 1000 °C приведены в таблице.

Выделение вторичных карбидов при непрерывном охлаждении

В дальнейшем мы для простоты будем считать зависимость равновесной доли карбидной фазы в данном сплаве от температуры линейной:

f равн »у ( T s - T ) ,

где fравн(Ts -AT)- fравн(Ts) A T

Значения у ₂₀₀ (для A T = 200 °C) также приведены в таблице.

Выразим из (4) с учётом (5) время изотермического достижения заданной доли карбидной фазы f К:

In t = 1ln( f К - fr ) - ¹h( T _s - T ) - In^ y ¹ n ) + Q- .                                (7)

n            n                    RT

Приравняв к нулю производную этого выражения по температуре, можно найти положение «носа» С-образной кривой выделения карбидов:

или

T - T « R ^T s-sm _nQ

.

₌ nQ f L , 4 RTs _ /

2 R bl nQ ,

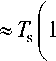
RT ) nQ J

Далее воспользуемся приёмом, который был применён в [13, 14]: разложим ln t в ряд около температуры минимума T m и удержим в нём два первых члена:

ln t (T) ~ In t ( T m ) + | ( T - T m ) ² ,

d2lnt где | =--- dT2

имеет смысл кривизны изотермической диаграммы вблизи «носа». Дважды

T=T ^{1 1} m

дифференцируя (7), можно найти, что

1 =1--^ + 2 "Q |1

n (T_s - T m ) ²     RT _S 3 V

—

x-3

RTS)

---- I ~ nnQ J

RT _S J

,

и с учётом этого из (7) и (10) получаем или

t =-----TT aDo y1 n

f нач

^{( f} К ^{- f} К   )

V

nQ ₁

RT s² j

1n exp

Q1- 1

^RTm J

exp

n Q i

2 RT ²

( T m -

T ) ²

V = (f К - fr )1" =aD»l

₂ 1 n RT _s

V nQ i J

exp

—

RT

exp

—

2 V RTs2 J

( T _m -

T ) ²   • t .

Заметим, что зависимость нового параметра v , пропорционального времени t , от f_K не содержит температурно-зависимых параметров. Это означает [15], что превращение является изокинетическим и его развитие в ходе непрерывного охлаждения может быть описано интегралом Шейля – Штейнберга

- J -^-=1, / vt ( V , Т )

Ts где T - температура, при которой заданная величина v (то есть f К) будет достигнута в ходе непрерывного охлаждения со скоростью v. Если считать последнюю постоянной и вынести за знак интеграла, мы получим выражение, связывающее скорость охлаждения с долей превра- щения:

т

T s   _dT

v =  -------.

Г t ( V , Т )

Реально при T^ Ts время превращения t ^ да; однако при использовании приближённой формулы (10) такой результат получить нельзя, поэтому верхний предел приходится принять равным бесконечности. Полное количество карбидов, образовавшихся в ходе охлаждения, можно найти, положив T^ 0. Если использовать для t выражение (12), то удобно ввести новую переменную

x =

Q 1 RT _s ²

n ₂

( T m - Т ). Тогда интеграл (15) превращается в

интеграл Пуассона, равный Jn/2,

и

после необходимых преобразований окончательно получаем lnv = ln A - In ф = In A - -ln(f К - ^нач),

n где

A = a D ₀ y ¹ n n -^-2-^-n

I 1

RT Г^- n

Q 1 ,

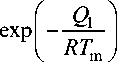
Следовательно, зависимость In v от ln( f К - f н^ач ) должна представлять собой прямую с угловым коэффициентом 1/ n . Такие зависимости для сплавов, для которых в [10] имеются данные о повышении M s при уменьшении скорости охлаждения, приведены на рис. 2. При этом значения ( f К - f н^ач ) рассчитывались по изменению M _s на основании формулы, предложенной в [12]:

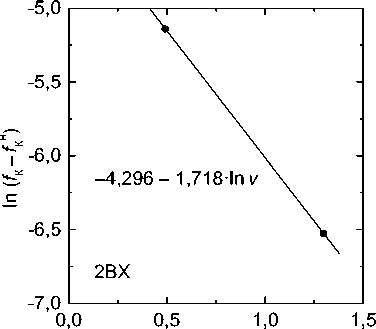
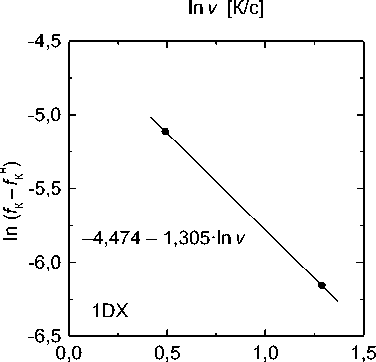
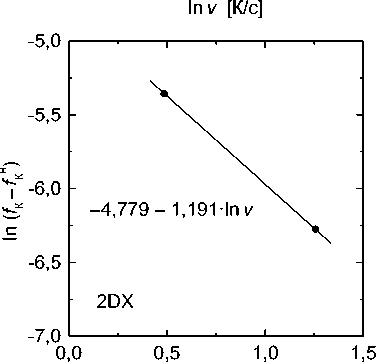
M s = 475 - 275 • C - 12 • Cr - 10 • C • Cr, °C, (18) где содержания элементов в аустените выражены в массовых процентах. Как видно, значения n колеблются в диапазоне 1,2–1,7; примем в среднем n = 1,5, что соответствует, как уже отмечено, теоретическому значению для случая роста мелких частиц.

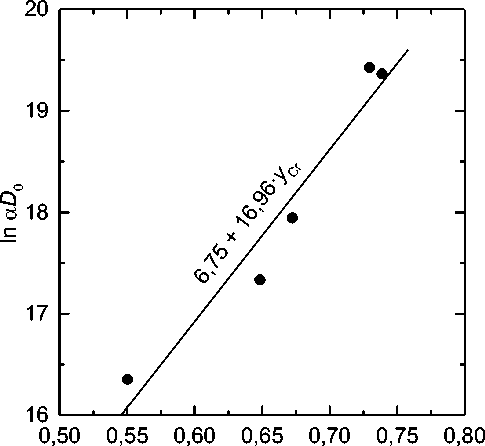
Если принять энергию активации роста карбидов Q1 равной энергии активации их растворения Q, которая описывается выражением (2), то на основании (17) можно определить из найденных по графикам рис. 2 значениям ln A величину параметра aD0, поскольку все остальные входящие в (17) параметры известны для каждого сплава. Величины ln aD0 показаны на рис. 3 в зависимости от атомной доли хрома в металлической подрешётке карбидов yCКr (бралась её равновесная величина при 1000 °C). Несмотря на некоторый разброс, наблюдается связь между этими двумя величинами, которую можно описать соотношением ln aD0 = 6,75 +16,96 • у К. (19)

Совместное использование выражений (16), (17) и (19) позволяет рассчитать для любого состава сплава долю выделившейся карбидной фазы после охлаждения с любой заданной скоростью. При этом входящая в (17) температура T s должна быть оценена исходя из количества карбидов, сохранившихся после окончания аустенитизации, а температура T m затем – по формуле (9).

ln v [К/с]

ln v [К/с]

Рис. 2. Зависимости ln v от ln( f _K — f Нач ) . Обозначения сплавов указаны на графиках

Fig. 2. Dependencies of ln v on ln( f К — f ™⁴ ) . Designations of alloys are indicated on the graphs

y при 1000 °C

Рис. 3. Зависимость параметра ln α D ₀ , рассчитанного по данным рис. 2 при n = 1,5 и значениям Q согласно формуле (2), от величины y ^К

Fig. 3. Dependence of parameter ln α D ₀ , calculated from the data of fig. 2 at n = 1.5 and Q values according to formula (2), on the value y ^К

Перлитный распад аустенита при непрерывном охлаждении

Описание кинетики перлитного распада в рассматриваемых сплавах в изотермических усло-

виях имеется в работе [9]. Согласно ему, превращение подчиняется уравнению Аврами f ( t ) = 1 - exp ( - K ( T ) - t n ) , в котором коэффициент K описывается формулой m K 1 n = C -f T s   T ) eXp f- H_ ) . 1 T J     V RT J

(20) (21)

Значения параметров уравнения (21), подобранные в [9] на основании экспериментальных данных, равны m = 3;

T s = 760 ° C;

U = 288,9 + 10,9 - Cr - 86,8 - C + 4,9 - Cr - C , кДж/моль;

n = 9,50 - 0,91 - Cr - 2,85 - C + 0,50 - Cr - C ; In C = 39,74 + 0,86 - Cr - 9,58 - C + 0,69 - Cr - C , с-1.

(22)

Переход к условиям непрерывного охлаждения может быть осуществлён так же, как это было сделано в предыдущем разделе. Если приближённо заменить изотермическую С-образную кривую, определяемую выражением (21), квадратичной параболой

In t(T) «In t(Tm) + ^П (T - Tm )2 , (23) где температура «носа» С-образной кривой изотермического образования перлита Tm, при которой производная выражения (21) обращается в ноль, равна

f    mR m I T s    U J , а , d 2ln t       f 1 + mRTjU У 5 =-- у   = m ------— , 2 dT    t—t     V 1 s 2m J 1  1 m

(24) (25)

то из общих выражений, связывающих долю перлита f с (постоянной) скоростью охлаждения v , полученных в [14], можно вывести следующее выражение:

/ 1 n    -1     (T - Tm)m+1   f  U ) Л m T T - Tm ) v = (-ln(1 -f)) nJ—C —--m^—exp--erfc J---s---m , V   X       4 m    Ts Tm-1    4 RTm J   VV 2 Tm Ts - Tm J (26) фактически описывающее термокинетическую диаграмму образования перлита. Напомним, что m = 3, а значения остальных параметров находятся исходя из химического состава у-фазы к моменту окончания аустенитизации (с учётом её температуры и продолжительности) по формулам (22).

Результаты расчёта

На рис. 4 представлены результаты расчёта по описанным теоретическим моделям термокинетических диаграмм превращения аустенита в нескольких сплавах в сравнении с экспериментальными из [10]. Видно достаточно хорошее согласие экспериментальных и расчётных диаграмм в обоих случаях.

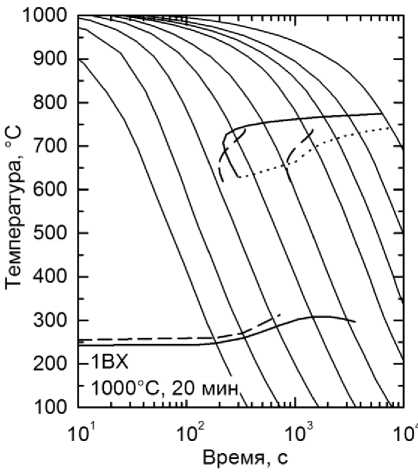
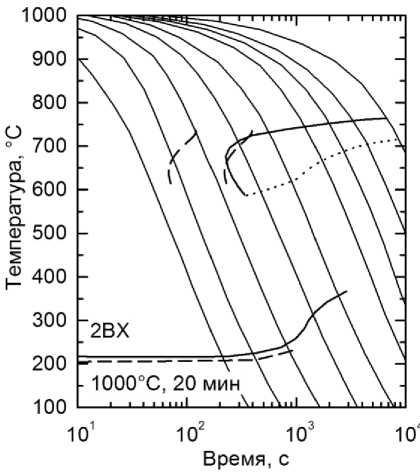
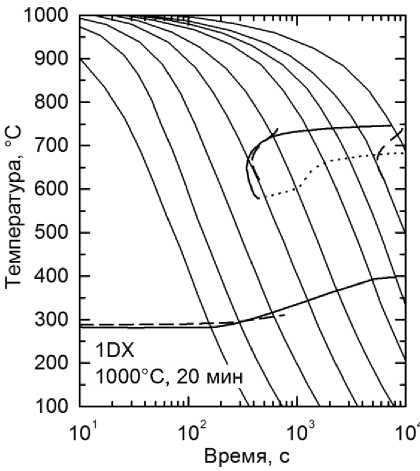
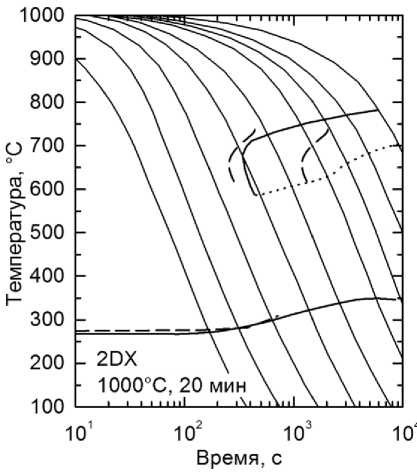
Рис. 4. Рассчитанные термокинетические диаграммы распада аустенита в сравнении с экспериментальными из [10]. Линии начала и конца перлитного превращения соответствуют долям распада 0,01 и 0,99 соответственно. Обозначения сплавов указаны на графиках

Fig. 4. Calculated thermokinetic diagrams of austenite decomposition in comparison with the experimental ones from [10]. The lines of the beginning and end of the pearlite transformation correspond to the decay fractions of 0.01 and 0.99, respectively. Designations of alloys are indicated on the graphs

Выводы

• 1.    Разработана кинетическая теория выделения вторичных карбидов из аустенита при непрерывном охлаждении и определены концентрационные зависимости её параметров для высокохромистых сплавов системы «железо – хром – углерод».

• 2.    Разработана модель эвтектоидного рас-

• пада аустенита в этих же сплавах при непрерывном охлаждении.

• 3.    Сравнение результатов расчёта (повышения мартенситной точки вследствие выделения карбидов и положения линий начала и конца перлитного распада при непрерывном охлаждении с различными скоростями) с экспериментом показывает достаточно хорошее согласие.