Кинетика разрушения волокнистых композитов с упругопластической матрицей

Важной особенностью механического поведения структурно-неоднородных материалов под нагрузкой является закритическая стадия деформирования, сопровождаемая падением напряжений при прогрессирующих деформациях [1.2]. Причиной разупрочнения деформируемых сред является деструкция различной природы, например, разрушение отдельных элементов структуры: волокон [3] или слоев [4]. фазовые превращения и динамическая рекристаллизация [5].

В плане анализа механизмов закритической деформации на основе математического моделирования рассмотрим процессы структурного разрушения волокнистых композитов регулярной структуры с упругопластической матрицей при нагружении в поперечной плоскости.

Вопросы неупругого деформирования волокнистых композитов постоянно привлекаю! внимание исследователей. В частности, получили распространение численные методы моделирования, которые позволяют представить среду в виде системы дискретных элементов и рассматривать диссипативные процессы как многошаговые повреждения структуры модели с учетом существенно неоднородного распределения структурных напряжений и деформаций [6-9].

Рассмотрим периодическую задачу теории малых упругопластических деформаций для рассматриваемой неоднородной среды матричного типа с регулярной структурой, состоящей из уравнений равновесия

• (1) геометрических соотношений Коши

определяющих соотношений при активном нагружении

К6,, 8 ц + С-(1 gj^cfkd .t + 5fi8,k ~ ^5ц8ц j линейных уравнений связи приращений напряжений и деформаций при разгрузке.

Модуль объемного сжатия KQ"^ и модуль сдвига G’(r) являются кусочнооднородными периодическими функциями. Пусть а- вектор трансляции, смещением на который ячейки периодичности можно синтезировать структуру материала. Условия периодичности для искомых полей деформирования

щ(г) = г/,(г+ л), й-Д^^б’Дг+я), о-?(г) = о-Дг+а)          (4)

и заданные макродеформации определяющие условия в перемещениях на границе ячейки периодичности Г7

иАг^бцГ).                                                  (6)

позволяют выделить единственное решение системы (1-3) при определенном виде функции неупругого деформирования g.

Пусть для упругого волокна g-О, для матрицы g является функцией второго .(2)

инварианта тензора деформаций J и описывает поведение упругопластического материала с линейным упрочнением: jo-

.12) _ ГГ~.~    ...           I

J г ~ V ^S es ’ е5 e,j ' g ^   ’ где J -предел упругости, ы - модуль сдвига и О - модуль, упрочнения.

Кроме того, дополним постановку задачи условием разрушения материала матрицы. При достижении вторым инвариантом тензора деформаций своего критического значения

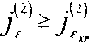
материал матрицы теряет способность сопротивляться формоизменению сохраняя лишь способность сопротивляться гидростатическому сжатию

(g=n.

J_E ~ £1 1 + ^22 <-33

Последовательное решение рассмотренной краевой задачи при различных уровнях макродеформаций позволяет в рамках вычислительного эксперимента проследить кинетику структурного разрушения композиционного материала и вызванное этим процессом изменение его эффективные свойств, характеризуемых связью макродеформаций gy и макронапряжений

(Ю)

Численные расчеты были проведены методом конечных элементов для симметричной части ячейки периодичности находящегося в условиях плоского

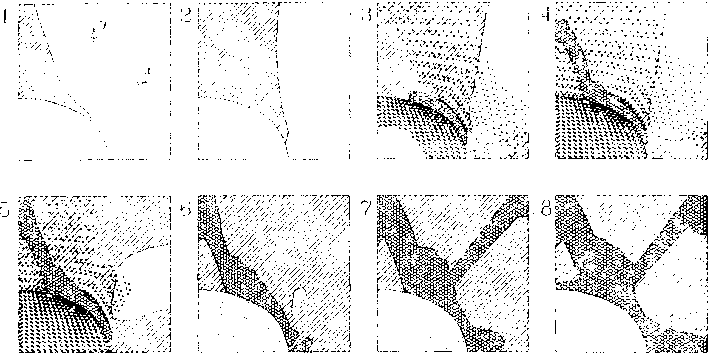
Рис. 1

Кинетика разрушения упругопластическом матрицы при деформировании волокнистого композита (,?* = 0, g_v < 0)'

l _J - зона пластичности:

зона разрушения

деформированного состояния композита с тетрагональным расположением эллиптических в поперечном сечении волокон при следующих характеристиках:

G_m - 2.1 х 10³ МПа, G; = 0.05 х G_m. К_т = 3.5 ■ 10³ МПа, /^ = 0.01.

= 0.025, G_f = 2.1 х 10⁵ МПа, _Vf = 0.25.

Индексами т и]' отмечены характеристики соответственно матрицы и волокон.

Исследуемая область была разбита на 1150 треугольных конечных элементов. Линеаризация рассмотренных определяющих соотношений осуществлялась с использованием метода дополнительных напряжений при поэтапных нагружениях [10.11]. Решение краевой задачи производилось при пропорциональном увеличении (или уменьшении) компонент тензора макродеформаций с шагом от 3 х 10 6 до 3 х 10

На рис. 1 показана последовательность возникновения и развития зон пластичности и разрушения в матрице при одноосной деформации сжатия волокнистого композита (объемная доля волокон 0.188, отношение полуосей эллипса 2/3). Здесь и далее состояния материала, отмеченные на диаграммах, характеризуются формой и расположением зон неупругого деформирования, показанных на изображениях фрагментов ячейки периодичности с соответствующими номерами.

Как видим, необратимые изменения в структуре материала приводят к нелинейности на диаграмме деформирования. Скачкообразное подрастание зон разрушения на некоторых этапах деформирования вызывает появление срывов на диаграмме. Точками отмечены конечные элементы, в которых происходит упругая разгрузка среды по второму инварианту (d { <0). что объясняется перераспределением напряжений в процессе структурного разрушения. Обнаруженное явление локальной разгрузки при активном деформировании композита более детально исследовано в работах [4.12]. В данном случае, вклад матрицы в сопротивление внешней нагрузке на заключительной стадии деформирования композита ограничивается, в основном, ее сопротивлением уменьшению обьема. Этим и объясняется сближение значений макронапряжений ст, и (у_у .

На рис. 2 показаны диаграммы и основные этапы деформирования композита при чистом формоизменении (равновеликая двухосная деформация, растягивающая в направлении оси х и сжимающая вдоль оси у). На диаграмме зависимости макронапряжений от макродеформаций в данном случае появляется ниспадающая ветвь. Разупрочнение композита вызвано процессом структурного разрушения. При этом обнаружено чередование постепенного и скачкообразного подрастания зоны разрушения при монотонном макродеформировании.

Обращает на себя внимание прохождение зависимости cr*^*) через нулевую отметку на оси ординат при увеличении деформации. Смена знака макронапряжений <у_х свидетельствует о том, что. вследствие развития зоны разрушения в матрице, теперь уже композит, в свою очередь, теряет способность сопротивляться формоизменению.

Кроме отмеченного эффекта локальной разгрузки, проведенные расчеты выявили процессы повторной нагрузки пластических элементов, что приводит к уменьшению зоны упругой разгрузки. Например, эго явление проявилось при переходе от состояния, помеченного цифрой 6, к состоянию - 7 (см. на рис. 2).

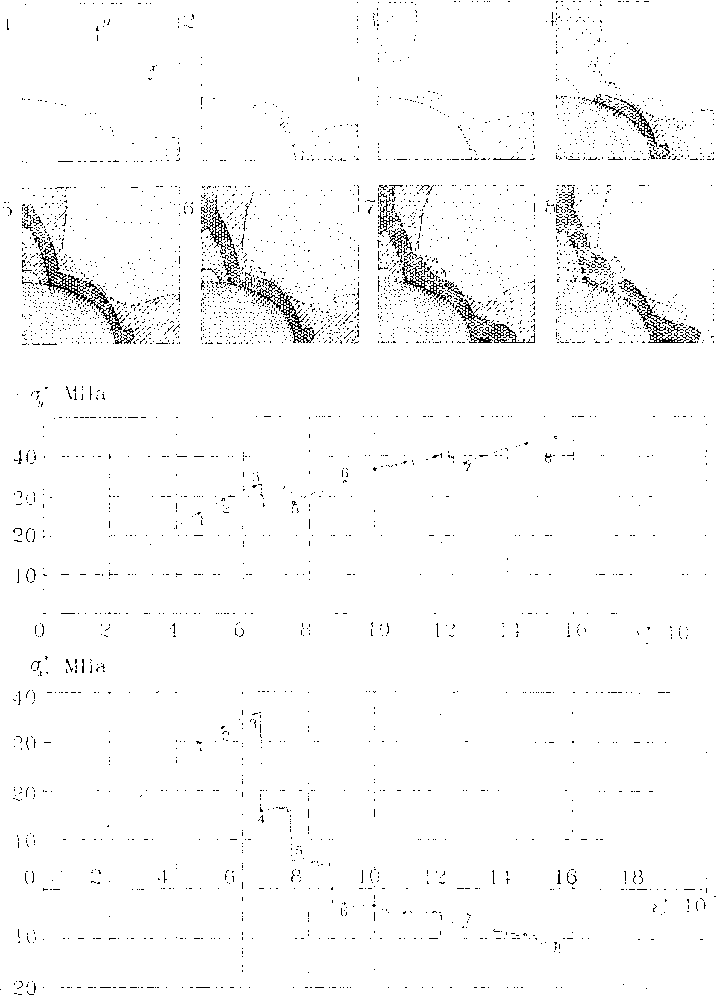
Рис. 2 Кинетика разрушения упругопластической матрицы на закритической стадии дефорамирования волокнистого композита ^* = - f*j :

EZZ3 - зона пластичности: Е>23 - зона разрушения

Резулъш;- расчетов показали, что увеличение доли волокон в объеме композита до 0.37" не приводит к существенному изменению характера деформирования. Как и в рассмотренных случаях, начальная стадия разрушения матрицы связана с объемом материала вблизи межфазпой границы. хотя отмечено и образование небольшой изолированной зоны разрушения в матрице. Кроме того, в качестве особенностей можно отметить появление ниспадающей ветви на диаграмме <т*^*) при макродеформировании по схеме гд ~ —0.5 ^ > О и более локализованное развит ие зон пластичности и разрушения.

Таким образом, полученные результат математического моделирования позволяют сделать вывод о возможности равновесного протекания взаимосвязанных процессов упругопластического деформирования и разрушения, сопровождаемых локальными явлениями упругой разгрузки и повторного нагружения, в структуре однонаправленных волокнистых композитов при заданных программах деформирования. Возникающая ’ при этом нелинейность диаграмм макродеформирования в отдельных случаях настолько велика, что имеет место ниспадающая ветвь, а величины компонент тензора макроиапряжений могут не только снижаться до нуля, но и менять свой знак.