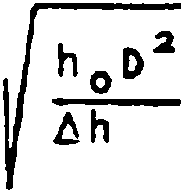Киноформные оптические элементы с увеличенной глубиной фокуса

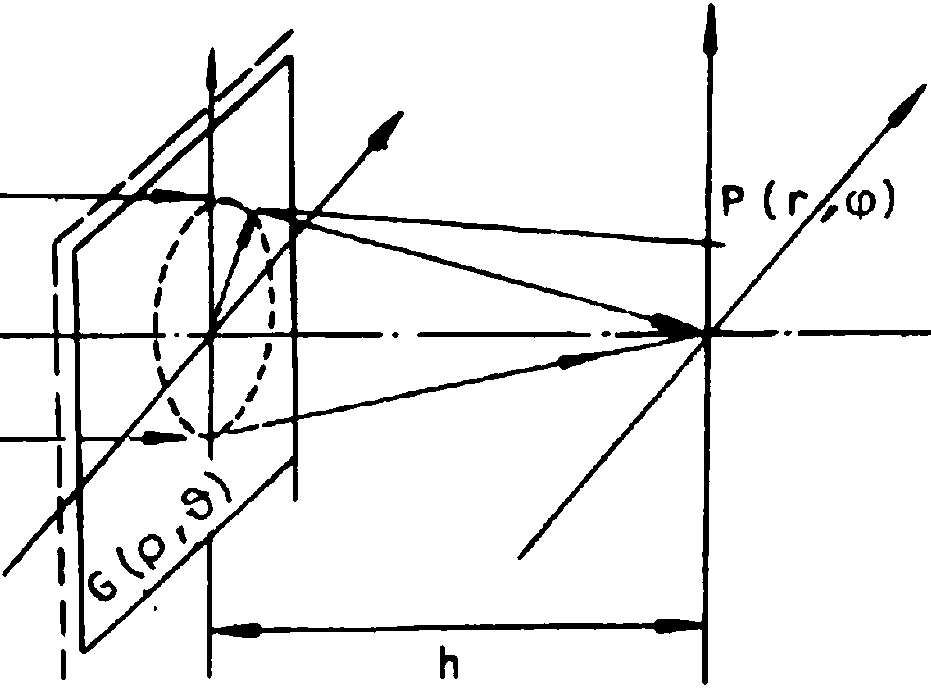
Распределение интенсивности света в фокальной плоскости хорошо коррегирован-ного объектива обусловлено дифракцией на выходном зрачке. Продольный и поперечный размеры каустики вблизи фокуса жестко связаны: чем меньше размер пятна в геометрической фокальной плоскости, тем меньше глубина фокуса. В последнее время возрос интерес к оптическим системам, не обладающим этим фундаментальным ограничением. При конструировании оптических систем с увеличенной глубиной фокальной области необходимы оптические элементы следующих двух типов. Во-первых, элементы, изображающие осевую точку в виде отрезка прямой, расположенного вдоль оптической оси, и не осуществляющие проективных преобразований. Такой тип фокусировки называется аксиконным. Используется он для получения оптического разряда в газе [l], для создания опорной световой линии в метрологии [2], для бесконтактных измерений перемещений отражающей поверхности в специализированных микроскопах [З] , в оптических дисковых системах звукозаписи и воспроизведения [^] . Во-вторых, элементы, удлиняющие каустику без изменения проективных свойств оптической системы, что необходимо в микроскопах совмещения установок рентгенолито-графии с использованием синхротронного излучения [5]> устройствах ввода-вывода изображений из ЭВМ [6] , в лазерных технологических установках [7] .

Традиционные оптические элементы далеко не всегда позволяют эффективно управлять каустикой в перечисленных задачах, поэтому представляет интерес разработка новых оптических элементов и, в частности, киноформов. Настоящая работа посвящена расчету киноформных аксиконов и обобщенных зонных пластинок (ОЗП) со специальным распределением интенсивности вдоль фокального отрезка и обсуждению результатов экспериментального исследования их.

Задача расчета комплексной функции пропускания киноформа для заданного распределения интенсивности в области фокусировки обычно допускает несколько решений. Поэтому особое значение имеет построение феноменологической модели оптической задачи, на основании которой выводятся уравнения, позволяющие рассчитывать и оптимизировать фазовую функцию пропускания и топологию киноформа.

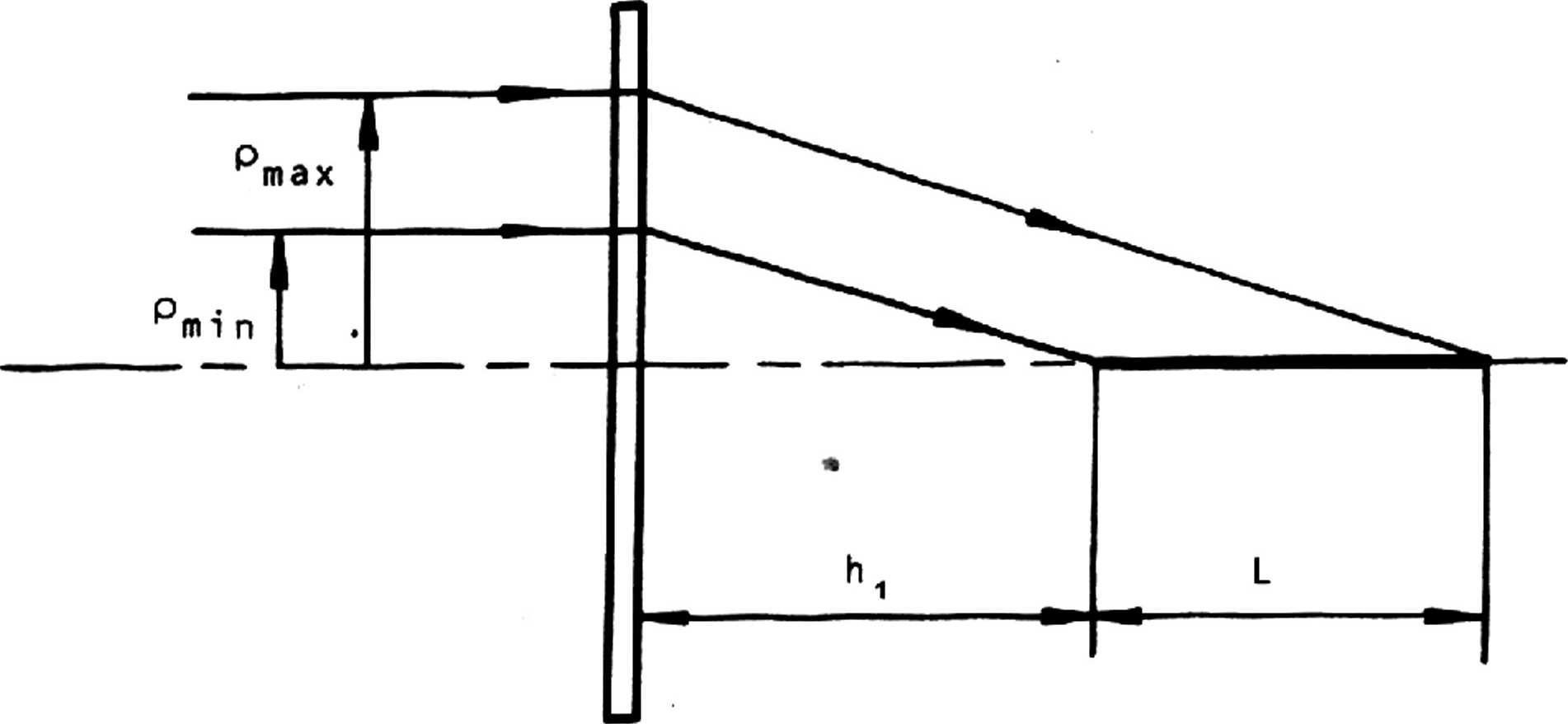
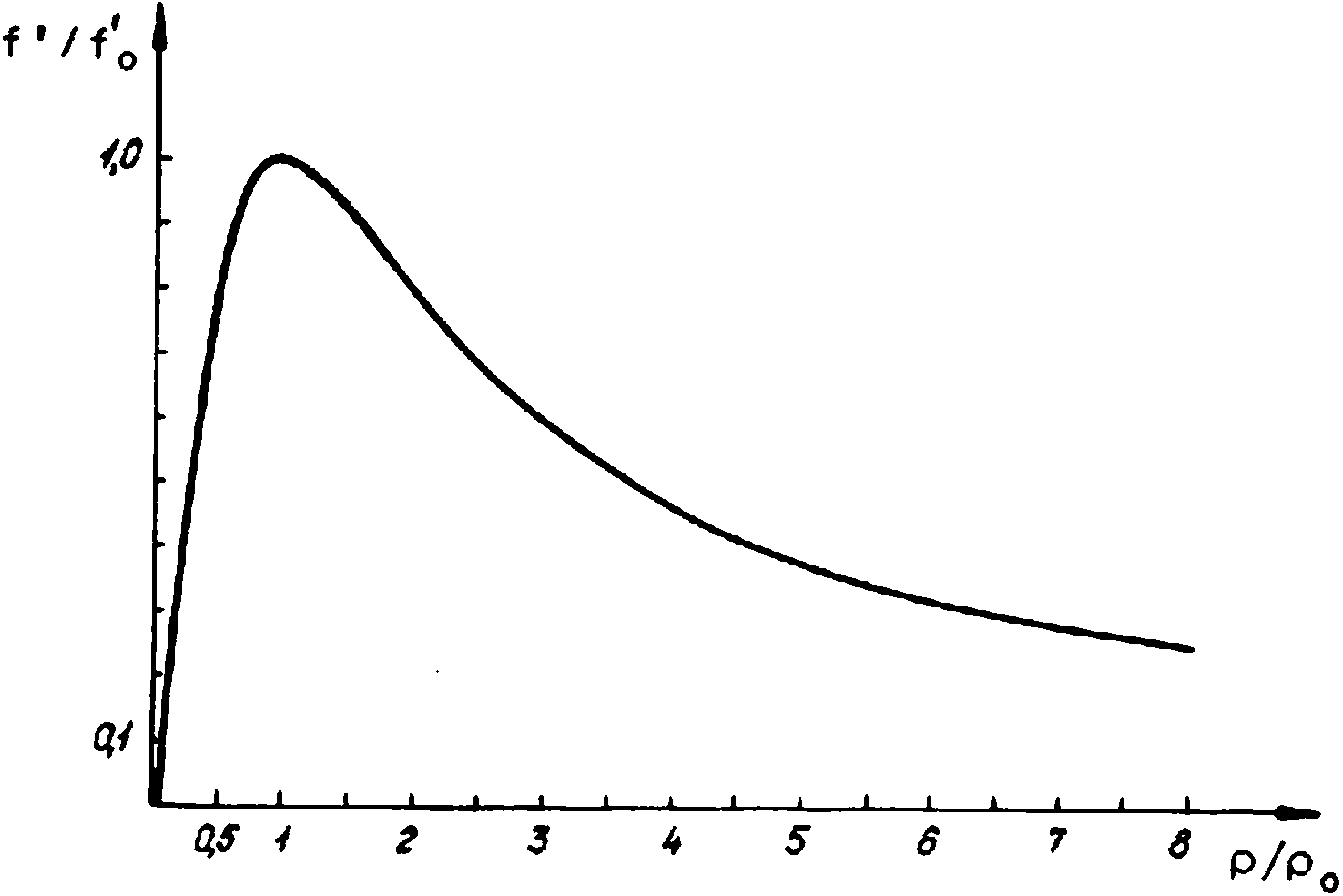
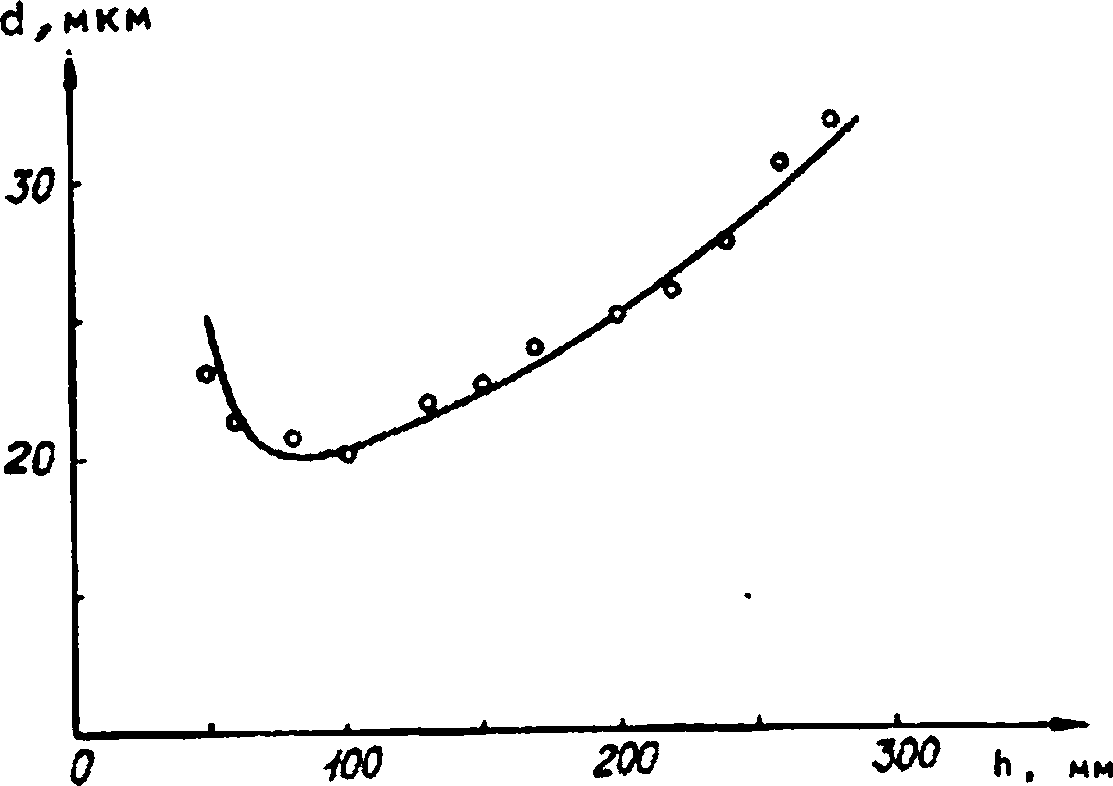
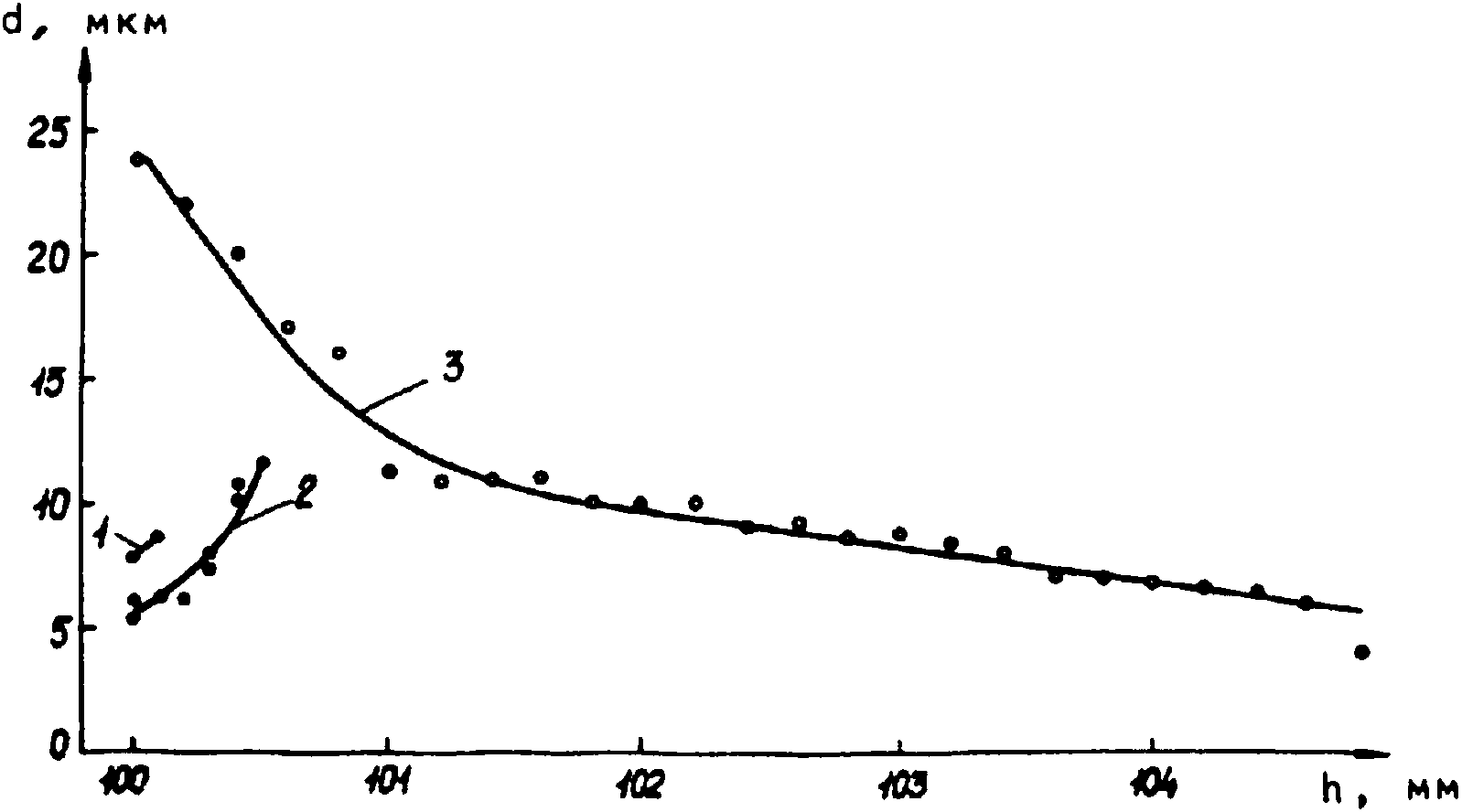
Хорошо известны [8,9] решения уравнения Гельмгольца для световых волн, распространяющихся в однорядной среде от бесконечного линейного источника:

U(rz

Выражение (1) можно представить в наглядном виде для больших значений г > —:

U(rzVzzzt) = —-- exp[i(2nur + 2n£z + lep - j - -~ - cot) ] z(2)

П\/ц7                              42

где модуль волнового вектора к = 2п х/ц^+^ относится к частоте света f как k = 2nf/cz а компоненты волнового вектора имеют вид:

к = 2пц7/|г|, к = 2nC*/|z|z к =0. гz

Волновой фронт наклонен под углом, равным arctg(C/u) к оси г, вдоль которой расположена бесконечная светящаяся линия.

Фазовая функция в показателе экспоненты (2) описывает цилиндрические, конические и винтовые волновые фронты. В работе [8] показано, что можно записать выражение для комплексной функции пропускания киноформа, фокусирующего в линию, выбирая коэффициенты (ц#С#1) и определяя соответствие координат плоскости киноформа, рабочей апертуры и фокусного отрезка.

Таким образом, целесообразно проводить расчет функции пропускания киноформов, имеющих каустику в виде фокального отрезка, предполагая, что плоский волновой фронт преобразуется ими в конический, цилиндрический, винтовой либо в их комбинацию.

Рассмотрим способ расчета киноформных аксиконов, позволяющий получать заданное распределение интенсивности вдоль фокального отрезка.

КиноФормные аксиконы

В отличие от случая дифракции на отверстиях различной формы и на линзах фокальный отрезок семейства аксиконов формируется в ближней зоне дифракции, где амплитуда поля определяется окрестностью соответствующих критических точек, расположенных в плоскости G оптического элемента (рис. 1). Для нахождения дифракционного интеграла Френеля используется метод стационарной фазы [10]. В паракси-

Uo(р,е)

Рис. 1. Схема прохождения светового пучка через киноформ к записи интеграла Френеля

альном приближении поле U(r,h) в произвольной точке области фокусировки аксико- на с фазовой функцией пропускания f (р) описывается выражением:

U(r,h)

ikU0(p)f*(p)J (rkf ') /---------

Vl+hfn(p)

exp (i k [h +

♦ ^~- ♦ f

+ ^

где

.       2п.

к = -г-

Jo(«) - функция Бесселя нулевого порядка;

(•)* - штрих используется для обозначения производной функции;

Uo(р,0) - амплитуда фокусируемого волнового фронта в плоскости G.

Из выражения (3) следует, что поперечное распределение интенсивности в фо кальном отрезке описывается функцией Бесселя нулевого порядка. Диаметр фокального пятна находится обычным образом:

d = 5/(kf 1 (р)),                                                                       (4)

То есть область фокусировки имеет вид тела вращения, и ее поперечный размер изменяется вдоль оптической оси. Характер этого изменения определяется конкретным видом зависимости f*(p).

Для киноформного аксикона р, h и f (р) связаны следующим соотношением: fe(p)h

Р = "——     - ^ -1 'h.                                                (5)

- f 12 (P)

В приближении Френеля-Кирхгофа амплитуда поля U(O,h) в произвольной точке на оптической оси имеет вид:

U(Ozh) = -ikU0 (р)exp [ik[f(p) + Ур2 + h2] ♦ in/4} *

x f*(p)|/ --------------------;---------- .                                                 (6)

У r (p)-f*(p)(1-f a(p))/p

С помощью выражения (3) или (6) легко составить дифференциальное уравнение для функции пропускания киноформного аксикона, если задано распределение интен сивности вдоль фокального отрезка. Возможности предлагаемого метода расчета различного типа аксиконов как в параксиальном, так и в приближении Френеля-Кирхгофа более подробно рассмотрены в работе [11] ♦

Например, найдем в параксиальном приближении функцию пропускания f Ср) акси-кона, обеспечивающего постоянную интенсивность W на оптической оси по всей длине фокального отрезка. Если волновой фронт падающей волны плоский и ее амплитуда зависит только от радиальной координаты UQ(p), из (3) и (5) следует lU(0,h)|2 =     U=(p)1,2(p)/[i"(p) -         = W, откуда получаем дифференциальное уравнение, решаемое численно с учетом конкретного вида UQ(р):

„       f'(p)    f ,a(p)4naU=(p)

f (Р) - —---„--0.(8)

В частном случае Uo(p) = UQ=const удобно записать уравнение (8) в новых обозначениях f.(p) - f^L.l^fil. о,<9)

Р где а - ----- .

4наиа

О

Уравнение (9) допускает аналитическое решение, и функция пропускания f (р) определяется с точностью до трех постоянных a,bzc:

f (р ) = -aln(c-pa) * Ь.                                                            (10)

Постоянные интегрирования Ь, с, а также произвольно введенную постоянную а необходимо связать с требуемыми характеристиками фокального отрезка аксикона Срис. 2): длиной фокального отрезка L, его расположением относительно аксикона h1f диаметром фокального пятна в перетяжке d0 и местоположением перетяжки на оптической оси h0.

Рис. 2. Некоторые параметры аксикона и фокального отрезка, необходимые для определения функции пропускания: L - длина фокального отрезка; Ь1 - расположение его на оптической оси относительно плоскости G; Р р_,„ * внутренний и внешний диа-m 1 п шах метры рабочей зоны аксикона

Для этих целей наиболее удобны следующие два условия:

f"(PQ) = 0 - С = -Р§;                                                          (11)

f*(po) = < - а = - f^ •                                               (12)

Вид зависимости fl(p)/f*(Po) показан на рис. 3. Условие (11) определяет положение максимума функции f1(р), а условие (12) - величину этого максимума, и, соответственно, как следует из (4) и (5), - местоположение перетяжки на оптиче ской оси и радиус фокального пятна в перетяжке.

Рис. 3. Зависимость производной функции пропускания киноформного коноидного акси-кона f*(р)/f1(Ро) от радиальной координаты р/р0. Положение перетяжки фокального отрезка соответствует значению р/р0 = 1. По обе стороны от перетяжки величина диаметра возрастает

Параметры функции пропускания рассчитываются из требуемых характеристик фокального отрезка следующим образом. С помощью (М и величин do и X рассчитывается постоянная fу. Выражение (5) используется для расчета pQ по известным h0 и fy. В результате уравнение (10) принимает вид:

f(p) = f°роLn(р2+р2) + Ь.                                                        (13)

Внутренний Pm^n и внешний Ртах ~ радиусы рабочей зоны аксикона - рассчитываются с помощью выражений (13) и (5) по известным величинам L и h1. Постоянная b в выражении (13) позволяет смещать начало отсчета фазы, что необходимо при нумерации киноформных зон. Таким образом, все постоянные интегрирования определены и связаны с характеристиками аксикона.

Киноформы обычно изготавливаются по технологии фотолитографии (12), когда непрерывный фазовый профиль оптического элемента заменяется ступенчатым. Границы ступеней находятся из уравнения kf (р) = 2к(^ + п) ,                                                            ОМ где

N - число ступеней;

п - номер киноформной зоны, внутри которой расположена ступенька;

m - номер ступеньки. (Высота каждой ступени составляет 2п/М.)

Из (1^) следует, что радиусы зон аксикона с функцией пропускания (13) задаются равенством

Pm,n

n=0,1,2... m=Oz1z... N-1

Постоянная b выбиралась с учетом условия f(p • ) = 0.

Видоизменения поперечного распределения интенсивности в фокальном отрезке позволяют получать киноформы, объединяющие свойства аксикона и звезды Сименса, преобразующие плоский волновой фронт в конический по радиальной координате и винтовой - по угловой. Комплексная функция пропускания Т в этом случае имеет вид:

Т = exp [i kf (р) + i Id] или для традиционного конического аксикона:

Т = exp[ikop + 1Id]

где const;

целое.

Топология киноформных зон такого элемента не имеет осевой симметрии. Вследствие угловой зависимости фазы, киноформные зоны аксикона непрерывно сдвигаются вдоль радиуса на величину, определяемую I, преобразуясь в спирали. Для поля в произвольной точке фокального отрезка элемента с функцией пропускания Т при освещении плоской монохроматической световой волной единичной амплитуды легко получить следующее выражение:

ll(rz

V2nk a exp 1 (kh + —^ - -^—)

* е' ^ J I (каг) Уь ,

Таким образом, вдоль фокального отрезка фаза волны изменяется по винтовому закону, а амплитуда определяется функцией Бесселя не нулевого, а 1-го порядка

J^C»), что и свидетельствует о "раздвоении" линии в поперечном сечении.

Существенной особенностью аксиконной фокусировки, ограничивающей область ее применения, является низкая концентрация излучения. Как показано в работе [11], при фокусировке излучения аксиконом интенсивность на оси в 1000 раз меньше, чем-при фокусировке соответствующей сферической линзой. Именно поэтому представляет интерес возможность изменения каустики линзы путем введения контролируемых абер раций.

Ниже представлены способ расчета и результаты экспериментального исследования обобщенной зонной пластинки.

Обобщенные зонные пластинки

Традиционная линза концентрирует весь освещающий ее световой поток в фокальную точку. Сквозь любую круговую зону в плоскости выходного зрачка, заключенную между радиусом р и (р + Др), протекает поток лучистой энергии мощностью ды(р)   2пр и^о^и*^) ДР

где U(p) ” амплитуда освещающей волны в плоскости линзы.

Рассчитаем дифракционный элемент, концентрирующий эту мощность в область, расположенную вдоль оптической оси между ho и (hQ + Ah) .

Из принципа таутохронизма в приближении малых углов дифракции для киноформ ных оптических элементов, фокусирующих излучение, следует условие, связывающее фазовую функцию пропускания Ф(р) и фокусное расстояние hl d^M = _ 2 dp          h *

Объединяя (18) и (19), находим распределение

мощности потока лучистой

эне р-

гии вдоль фокального отрезка:

AW(p) Ah

2nD U(P)U*(P)

znD U(0)U*(0)

d dp

\dp/

откуда следует уравнение для определения фазовой

Требуя

AW (р) Ah

например, постоянства мощности вдоль

const, hQ = const.

получаем

dO _ dp

и(р)и* (р)         .

и СО)U*СО) °Р ^о

Будем считать, что освещающая волна плоская,

функции пропускания ОЗП. фокального отрезка однородная, монохроматическая

и имеет единичную амплитуду. Аналитическое решение удается получить также для ^тах гауссовой волны. В приближении ------ « 1 уравнение (.22) разлагается в ряд

Тейлора, что значительно его упрощает:

Ф (р) = О - ~ f р [1 -      / pdp} dp .

Проводя интегрирование, имеем

ф(р) = ® - ^_ {£а . s£e2 }.

Из выражений (19) и (24) находим соответствие между точками фокального отрезка и радиальной координатой ОЗП:

h(p) = -                 ---- )(25)

1 -п^р2/* dp° или в том же приближении, что и (23):

Нр) • fi0(1 ♦ 5^>.(26)

о

С помощью (26) определяем постоянные £, "hQ:

р = 0 h = h0 = h0                f с = ^2

p = D h = ho + Ah = h0 + n£D2j fiQ = hQ •^

Таким образом, фазовая функция пропускания (24) получена в приближении г— « 1, что равнозначно требованию малости глубины фокуса по сравнению с фокус-п о ным расстоянием.

Границы ступеней киноформных зон находим в соответствии с уравнением (14):

Pm, п

4дЬХ .m

Da N

В приближении — « 1 получаем: h о

Pm = V2Xho

где первый член суммы описывает границы ступеней обычной ЗП с киноформным профилем зон, а второй появляется при ненулевых значениях ДЬ.

Разбиение на зоны можно выполнить более точно с помощью принципа таутохро-низма, когда радиусы зон ЗП рассчитываются из условия:

ha ♦ °m,n = [h * (S + П,Х]2-                                                   (30)

Объединяя выражение (30) и (26), получаем т,П <1 - 2(1 t n)XAh/D2        '                                        (31> что в приближении т“ « 1 дает:

%n = (mo(N + п) + [(N + п)Л1= + [(Е + nH^Ahh./D2 ♦

<32>

+ [ (^ + п)Х] 2ДЬ/(пО2))

Полученное равенство по сравнению с (29) содержит аберрационные поправки.

С помощью выражений (15) и (32) рассчитывалась топология фотошаблонов кино-формных аксиконов и ОЗП. Изготовленные образцы исследовались экспериментально.

Экспериментальное исследование

Проведены измерения следующих характеристик фокального отрезка: диаметра фокального пятна и распределения интенсивности в различных сечениях, плотности энергии вдоль оптической оси. Экспериментальная установка показана на рис. 4. Излучение одномодового He-Ne лазера 1 расширяется телескопом из двух объективов 2 и 3 и фокусируется киноформом 5- Диафрагма А позволяет изменять рабочую апертуру. Горизонтальный микроскоп 6 перемещается в пределах всего фокального отрезка. Апертура объектива микроскопа значительно превышает выходную апертуру исследуемых киноформов, и микроскоп не вносит собственных аберраций. Изображение фокальной точки наблюдается визуально либо переносится микроскопом в плоскость диафрагмы 7 фотоумножителя 8 с увеличением. Сигнал ФЭУ регистрируется самописцем или вольтметром. Перемещение фотоумножителя с диафрагмой осуществлялось микровинтом.

Рис. 4. Оптическая схема установки для исследования характеристик фокального отрезка: 1 * лазер; 2,3* объективы телескопа; 4 - апертурная диафрагма;

5 - киноформ; 6 - горизонтальный микроскоп; 7 - диафрагма; 8 - ФЭУ

Рассчитан и изготовлен логарифмический киноформный аксикон с двумя ступенями рельефа для излучения с длиной волны А. = 0,63•10— 2 мм, радиусом р = 6 мм, шах длиной фокального отрезка 1= 300 мм, Ь1 = 50 мм, диаметром фокального пятна в перетяжке d^ = 20 мкм. При проведении измерений влияние паразитных дифракционных порядков исключалось диафрагмированием апертуры аксикона. На рис. 5 точками представлены результаты визуального измерения диаметра фокального пятна вдоль фокального отрезка, сплошная линия соответствует расчетным данным, полученным с помощью выражений (4) и (I3) по фактическим значениям f’ и р0. Распределение плотности энергии вдоль оси фокусировки измерялось ФЭУ с диафрагмой 20 мкм после увеличения фокального пятна в 200 раз. Экспериментальные данные одной серии измерений представлены на рис. 6. Прямая линия строилась путем обработки результатов измерений по методу наименьших квадратов. Расчетная прямая параллельна оси абсцисс, то есть аксикон обеспечивает постоянную интенсивность на оси.

Рис. 5. Иллюстрация изменения диаметра фокального пятна киноформного аксикона вдоль оптической оси (координата h): ооооо - результаты измерений; расчетные данные

W, от н . ед.

"{ОО           200     1     300 h, ^м

Рис. 6. Распределение плотности энергии W вдоль фокального отрезка киноформного коноидного аксикона: оооооо - экспериментальные данные

Исследовалась также каустика ОЗП. Характеристики ОЗП: фокусное расстояние h - 100 мм, длина фокального отрезка ЛЬ = 5 мм, радиус р =10 мм. Одновре-о                                                                                                       гл а х менно аналогичные измерения проводились для объектива с фокусным расстоянием 105 мм и линзы со сферической аберрацией (h0 = 105 мм). На рис. 7 приведены экспериментальные зависимости изменения диаметра фокального пятна вдоль каустики: кривая 1 - объектив, кривая 2 - аберрированная линза, кривая 3 " ОЗП. Рис. 7 хорошо иллюстрирует удлинение каустики ОЗП. Однако не меньший интерес представляет и распределение плотности энергии вдоль оси каустики (рис. 8). Кривые 1 и 2, соответствующие объективу и линзе, для удобства изображения сдвинуты по оси абсцисс, максимум каждой кривой совпадает с фокусом, а плавное спадание наблюдается по обе стороны от фокуса. ОЗП дает несколько пиков интенсивности на оси, как показывает кривая 3. Вторичные пики вызваны, по-видимому, интерференцией паразитных дифракционных порядков. Проводилось также сканирование увеличенной дифракционной картины точечной диафрагмой (20 мкм) в различных сечениях фокального отрезка. При движении вдоль каустики в пределах 100-101 мм пятно практически совпадает с кружком Эйри, затем боковые лепестки воз-1 растают, достигая от максимума, что соответствует величине боковых лепестков при аксиконной фокусировке.

Рис. 7. Экспериментальная кривая изменения диаметра фокального пятна d обобщенной зонной пластинки вдоль каустики

W, отн. ед.

о ।         ........।-------------1        ■   ।             t—------_w_

/00         «И         «2         «3        W h, мм

Рис. 8. Экспериментальная кривая распределения плотности энергии W вдоль оси каустики: h - координата вдоль оптической оси

Выводы

Совпадение результатов расчетов с экспериментальными данными подтверждает возможность расчета киноформных аксиконов и ОЗП по рассмотренным методикам. Получить специальное распределение интенсивности вдоль фокального отрезка кино-формного аксикона возможно путем согласования распределения интенсивности в поперечном сечении лазерного пучка и фазовой функции пропускания. Если интенсивность на оси фокусировки сохраняется постоянной, то диаметр фокального пятна существенно изменяется. ОЗП также обладает каустикой с увеличенной глубиной. Но следует отметить бо'льшие по сравнению с аксиконом колебания интенсивности и изменения фокального пятна вдоль оси фокусировки.

В заключение автор благодарит Ю.И. Юрлова за помощь при изготовлении кино-формов и В.П. Коронкевича за полезные обсуждения.