Киральные метаматериалы: свойства и применение в терагерцовом диапазоне

Радиопоглощающие метаматериалы (РПМ) – ветвь искусственно созданных структур, получившие распространение благодаря своей способности полностью поглощать электромагнитные волны с использованием элементов, размеры которых значительно уступают длине волны [1]. Это открывает возможности для их применения в таких областях, как технологии малозаметности, сбор энергии, различные сенсорные приложения (активные экраны) и фотодетектирование. Эта группа метаматериалов может достигать высоких коэффициентов поглощения, близких к единице, особенно для так называемых «идеальных поглотителей». Типичная конструкция РПМ использует задний отражатель (зеркало), который препятствует пропусканию электромагнитных волн, так что при минимальном отражении может быть реализовано почти идеальное поглощение. Эти зеркала обычно содержат либо металлы, которые называются электрическими зеркалами, либо изотропные магнитные зеркала на основе метаматериалов. Электрические и магнитные зеркала меняют направление электрического и магнитного полей отраженной электромагнитной волны соответственно.

Киральные наноструктуры проявляют различные оптические свойства при взаимодействии с волнами эллиптической поляризации [2; 3]. Хи-роптические эффекты возникают из-за зависящих от структуры взаимодействий света с веществом высокого порядка, таких как дипольные и квадрупольные взаимодействия, которые могут приводить к разности фазовых задержек (называемой оптической активностью) или дифференциальному поглощению (называемому круговым дихроизмом).

Киральные метаматериалы, которые не пропускают падающий свет через свою структуру и демонстрируют высокий уровень поглощения, называются киральными метаматериальными

поглотителями (КММП). Высокое поглощение в РПМ может быть объяснено теорией интерференции, связанной с образованием полости Фабри-Перо [4] между верхним и нижним металлическими слоями. КММП, как правило, поглощают одну из компонент эллиптически поляризованного света, что приводит к большому дифференциальному поглощению. Это явление КММП широко используется в различных приложениях, включая болометрию, фотодетекцию, поляризационную визуализацию и спектроскопию.

Теории, используемые для объяснения основы поглощения метаматериалов, включают теорию согласования импедансов, теорию интерференции, резонансы Фабри-Перо, резонансы полости и теорию обычных линий передачи [4]. Собственные волны в киральных материалах можно охарактеризовать киральным параметром X , который обозначает силу перекрестной связи между магнитным и электрическим полями [5]. Материальные уравнения соотношений представлены в виде:

>>

D = sE + jxH ,(1)

——        ————

B = .Н + jxE,(2)

где s - диэлектрическая проницаемость;

• μ – магнитная проницаемость;

D и H – векторы электрической индукции и магнитной индукции соответственно, и они связаны как с электрическим полем (E), так и с магнитным полем (B). Эффективный показатель преломления киральных сред при падении лево-круговой и право-круговой поляризации равен:

n ± = n ± X ,                 (3)

где «+» и «–» обозначают лево-круговую и право-круговую поляризации соответственно;

n = J. .

Поскольку эффективные показатели преломления различны, поглощение и фаза имеют рас- хождение между круговыми поляризациями, что приводит к дифференциальному поглощению. Силу дифференциального поглощения можно выразить как:

п = — sin

[          1

I T + Г+ T -1² )

где T + и T - коэффициенты прохождения для волн лево-круговой и право-круговой поляризации соответственно.

Чтобы обеспечить теоретическую основу для работы и проектирования КММП, можно рассма- тривать КММП в качестве киральной среды, как показано на рисунке 1.

1           КЛ

>■            »»

Воздух Киральная среда Воздух п0, Zo             nt, Z             п0, Zo

R.R;

--------------► <

Рисунок 1. Иллюстрация коэффициентов пропускания (T) и отражения (R) киральных сред.

Вычислительные методы для проектирования КММП

Основные подходы для моделирования композитных киральных метаматериалов, включают в себя метод конечных элементов (МКЭ) и метод конечных разностей во временной области [6; 7]. МКЭ – это численный метод для решения задач, описываемых дифференциальными уравнениями в частных производных или тех, которые могут быть сформулированы как задачи минимизации функции. В этом случае интересующая область представляется как совокупность конечных элементов. Таким образом, непрерывная физическая задача преобразуется в дискретизированную задачу конечных элементов. Благодаря разделению физической задачи на геометрические структуры, можно достичь повышения точности при помощи увеличения числа элементов. Для задач с большим количеством узловых неизвестных, таких как уравнения Максвелла, МКЭ очень эффективен, поскольку локальность аппроксимации приводит к разреженным системам уравнений для дискретизированных задач. МКЭ решает физические задачи в шесть шагов:

• 6)    вычисление дополнительных параметров на основе глобального решения. Формулировка уравнений конечных элементов может быть выполнена методом Галёркина или вариационной формулировкой.

МКЭ применяется для электромагнитного моделирования КММП, раскрывая множество деталей о природе распределения электромагнитного поля, параметре киральности и плотности поверхностного заряда для различной направленности падающего эллиптически поляризованных волн. Этот метод используется в основе программных комплексов, таких как EMC Studio и HFSS [8].

Существующие методы проектирования и оптимизации КММП

Общепринятая практика проектирования КММП терагерцового диапазона предполагает использование отражающего слоя (металлического зеркала), изолированного от верхнего проводящего слоя диэлектрической прослойкой. В таких случаях диэлектрическая прослойка действует как резонатор Фабри-Перо, обеспечивая многократное отражение [4]. Этот слой отвечает за регулировку входного импеданса и гарантирует, что структура КММП идеально согласуется с волновым сопротивлением вакуума. Толщина отражающего слоя превышает глубину скин-слоя (оптически толстый слой), что блокирует проникновение падающих волн внутрь структуры, снижая потери на отражение и обеспечивая идеальное поглощение на резонансных частотах.

Дифференциальное поглощение возникает при активации поверхностных зарядов электрическими полями, что вызывает магнитный отклик. Генерируемый ток обусловлен взаимодействием падающей волны с магнитным и электрическим откликами гармонического поля. Если условие согласования импедансов [ Z ( ю ) = Z 0 ( ю ) J выполняется, усиление поля приводит к идеальному поглощению. В результате вся энергия падающей волны сохраняется в КММП.

Наличие отражающего слоя упрощает уравнение поглощения с A = 1 - R - T до A = 1 - R , поскольку T = 0 (где A , R и T - поглощение, отражение и пропускание соответственно). Поэтому отклик дифференциального поглощения ( п ) вычисляется по формуле η = A_ЛКП - А_ПКП , где A_ЛКП и А_ПКП , – поглощение лево-круговой (ЛКП) и право-круговой (ПКП) поляризации соответственно.

Рисунок 2 представляет собой пример КММП с обычным зеркалом, а также изображения изготовленных структур [9].

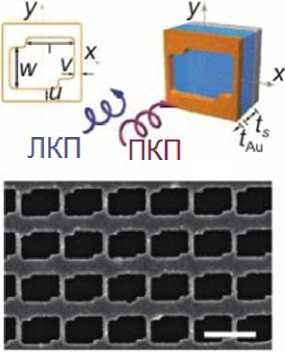
Рисунок 2. Метазеркала КММП [9]

Также перспективным направлением проектирования КММП является использование фотонно -кристаллических зеркал.

Киральные фотонные кристаллические зеркала, основанные на резонансе направляемых мод, а также одновременном возбуждении поперечно-электрических (TE) и поперечно-магнитных (TM) мод в фотонных кристаллических пластинах, способны реализовать частотно избирательное отражение циркулярно поляризованного света с сохранением направленности поляризации и круговым дихроизмом, близким к единице [10].

Для квази-2D структур достижение внутренней киральности при нормальном падении волны является сложной задачей. Это связано с тем, что внутренняя киральность возникает при одновременном возбуждении электрических и магнитных дипольных моментов в плоскости при нормальном падении, что ранее достигалось только в 3D киральных структурах [11]. Альтернативным решением является использование сложных многослойных киральных структур [12].

На рисунке 3 представлена схема тонкого фотонно-кристаллического зеркала с эллиптически поляризованной падающей волной с наклоном поляризации ψ [13].

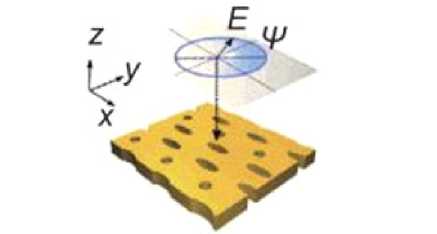
Рисунок 3. Схема тонкого фотонно-кристаллического зеркала [13]

Пропускная способность КММП

Пропускная способность КММП определяет раз-личные направления применения, включая зондирование, широкополосную оптическую связь, фотоэлектричество. В то время как узкополосные КММП идеально подходят для зондирования, широкополосные КММП хорошо себя показывают в приложениях оптической связи. В видимом диапазоне пики поглощения для левой (ЛКП) и правой (ПКП) циркулярных поляризаций могут возникать на разных резонансах при использовании плазмонных метаматериалов [14–16], а геометрия киральной структуры может приводить к формированию одиночных, двойных или множественных полос поглощения. Для достижения поглощения свыше 80% на разных длинах волн видимого диапазона была использована ŋ-образная металлическая резонаторная структура [17], размещенная поверх диэлектрической прослойки и металлического зеркала (рисунок 4). Изби- рательное поглощение для разных циркулярных поляризаций обусловлено конструктивной и деструктивной интерференцией падающего света.

Рисунок 4. Схема тонкого фотонно-кристаллического зеркала [17]

Представленная структура демонстрирует однополосный пик дифференциального поглощения, приписываемый дефектам изготовления. Достигнутые пики дифференциального поглощения приближаются к 0,9 и перекрывается с резонансом поглощения. Структура может быть принята для генерации горячих электронов, а также для избирательности по поляризации. Единая полоса пропускания охватывает диапазон от 440 до 470 ТГц [17].

Широкополосные хироптические эффекты с КММП могут быть реализованы путем объединения киральных резонансных мод двух асимметричных резонаторов [18]. Общая толщина отражающего слоя составляет менее одной девятой длины волны и, таким образом, поддерживает интеграцию на кристалле (рисунок 5).

Рисунок 5. Геометрия и изображение набора Zобразных киральных метаматериалов разных размеров [18]

Достижение узкополосного и сверхширокополосного высокого дифференциального поглощения нетривиально в планарных КММП, поскольку очень узкие или широкие пики дифференциального поглощения не обязательно транслируются в соответствующие резонансные хироптические эффекты. В результате методы достижения узкополосного идеального поглощения могут быть неприменимы для достижения высокого узкополосного CD. Тем не менее, подходы, которые интегрируют несколько структур разных размеров и/или составов на одной подложке, являются многообещающими. Это сильно зависит от геометрии киральной структуры и возбужденных мод.

Изготовление КММП

Киральные метаматериалы могут быть изготовлены с помощью подходов «сверху вниз» и «снизу вверх», используя различные методы. Подход «сверху вниз» использует такие методы, как литография ионного пучка; прямая лазерная запись и литография электронного пучка для фрезерования, резки и придания материалам желаемой формы, вида и порядка [19]. Подход «снизу вверх» состоит в использовании киральных элементов небольших размеров, объединяемых в более сложную структуру (композит). Процесс изготовления сопряжен со своими проблемами и ограничениями. Особенно для сложных конструкций, их изготовление может сильно отклоняться от теоретических предсказаний из-за несовершенств изготовления, в основном возникающих из-за грубой техники, а также характеристик подложки. Примером киральных структур, имеющих ярко выраженный резонанс являются Z-образные, L-образные и Γ-образные структуры [20]. Структуры с 3D-киральностью могут быть изготовлены с помощью прямой лазерной записи, осаждения под углом скольжения, литографии на ребре и осаждения, вызванного сфокусированным ионным пучком. Для киральных структур, состоящих из обеих пар зеркально отображенных элементов, только прямой лазерной записи недостаточно из-за проблем с отсечением электролитов. Сочетание подхода прямой лазерной записи с химическим серебрением предотвращает эту проблему. Изготовление планарных КММП схоже с изготовлением планарных киральных метаматериалов, которые обычно изготавливаются с помощью подходов «сверху вниз». Планарные структуры не могут обладать структурной ки-ральностью в 3D-пространстве из-за равенства недиагональных элементов в матрицах Джонса, которые возникают из-за плоскостной зеркальной симметрии [20]. Однако планарная структура метаматериала без какой-либо вращательной симметрии демонстрирует сильные хироптиче-ские отклики.

Заключение

В статье были рассмотрены эффекты поглощения электромагнитных волн терагерцового диапазона. Описан алгоритм на основании МКЭ для проектирования киральных метаматериальных поглотителей и представлены программные комплексы, реализующие их. На основании обзора литературы были выделены несколько вариантов реализации КММП терагерцового диапазона на основе метазеркал.

Также, были описаны методы получения узкополосных и широкополосных КММП. Однополосные КММП с узкополосным хироптическим откликом могут быть получены посредством одно- и/или двухрежимного возбуждения верхних киральных наноструктур, таких как Z-образные, L-образные и Γ-образные структуры [21]. Широкополосные КММП с широкополосными киральными эффектами могут быть получены путем тщательного размещения нескольких КММП с различными резонансами, обеспечиваемыми различиями в структурной геометрии и/или размерах киральных наноструктур [22]. Также были представлены методы изготовления КММП, в которых доминирует электронно-лучевая литография.

Киральные метаматериалы представляют собой прорыв в управлении светом, сочетая настраиваемые оптические свойства с миниатюрными размерами. Несмотря на технологические сложности, их внедрение в телекоммуникации, медицину и оптику уже меняет подходы к проектированию устройств. Будущие исследования могут привести к созданию «умных» материалов, адаптирующихся к внешним условиям в реаль- ном времени, что откроет новые горизонты для науки и техники.