Киральный метаматериал для частотно-селективной концентрации энергии сверхвысокочастотного излучения

В настоящее время идет активное развитие новых технологий энергосбережения. Одним из способов экономии электрической энергии является создание устройств, концентрирующих энергию различного происхождения с целью дальнейшего преобразования в электрический ток. Наиболее известными являются структуры для преобразования электромагнитной энергии оптического диапазона (например, солнечные батареи). Однако современный этап развития инфокоммуникационных технологий связан с активным использованием электромагнитных волн СВЧ-диапазона для передачи информации (технологии GSM, WiFi, LTE и т.д.). В связи с этим вновь возникает значительный интерес к разработке концентраторов электромагнитной энергии СВЧ-диапазона.

В отличие от аналогичных структур оптического диапазона, где преобразование энергии происходит напрямую, в случае СВЧ принципиальным является наличие концентратора (коллектора) электромагнитной энергии. Большинство известных решений создания коллекторов СВЧ-энергии базируется на использовании рефлекторов (зеркал), концентрирующих поле в своем фокусе [1-3]. Однако указанные и многие другие решения обладают рядом существенных недостатков, большинство из которых связано с большой массой и размерами концентрирующих энергию структур, невозможностью их конформного размещения на поверхности и т.п. В связи с этим возникает задача построения концентраторов СВЧ-энергии, принцип работ которых не основан на фокусировке СВЧ-энергии при помощи металлических рефлекторов.

В настоящее время активно проводятся теоретические и экспериментальные исследования метаматериалов, то есть композиционных искусственных структур, создаваемых на основе как минимум двух материалов. Подобные структуры проявляют весьма разнообразные свойства в СВЧ-диапазоне [4]. Обычно метаматериал состоит из контейнера, в котором периодически размещаются тонкопроволочные элементы какой-либо формы. Интерес представляет создание метаматериала, позволяющего на заданной частоте концентрировать электромагнитную энергию, поступающую из внешнего пространства вблизи своей поверхности или внутри себя. В [5] предложено использовать в качестве такой структуры метаматериал на основе элементов Телледжена, то есть разомкнутых колец с выступающими концами. Однако такие элементы с технологической точки зрения не являются оптимальным вариантом, так как их достаточно сложно располагать в контейнере. В данной работе проведен анализ отражения плоской электромагнитной волны СВЧ-диапазона от плоского бесконечного слоя метаматериала, состоящего из диэлектрического контейнера, в котором периодически размещены тонкопроволочные элементы в виде многовитковых спиралей. В силу зеркальной асимметрии используемых элементов такую структуру можно назвать киральным метаматериалом.

Задача об отражении волны от исследуемого метаматериала

Рассмотрим задачу об определении коэффициентов отражения и прохождения при падении плоской электромагнитной волны на планарный слой кирального метаматериала, который является бесконечно протяженным вдоль оси Oz . Геометрия задачи приведена на рис. 1. Пусть на ки-ральную структуру из диэлектрической области 1 ( 6', и ц_х – относительные диэлектрическая и магнитная проницаемости) под углом о падает плоская электромагнитная волна линейной поляризации (в статье рассмотрен случай падения волны с перпендикулярной поляризацией).

Область 2 на рис. 1 представляет собой слой кирального метаматериала толщиной h ( s^ и м^ – относительные диэлектрическая и магнитная проницаемости; х^ – параметр киральности). Частотные зависимости материальных параметров ^1 И /2 определяются типом резонансных элементов. Киральный метаматериал состоит из многовитковых тонкопроволочных спиралей, намотан- ных на диэлектрические цилиндрические оправки, которые равномерно размещены в планарном контейнере (см. рис. 2). Спиральный элемент описывается следующими геометрическими параметрами: N – число витков; R – радиус витка спирали; h – шаг спирали; l – длина спирали в расправленном состоянии; r – радиус проволоки. Спиральные элементы равномерно расположены в контейнере на расстоянии d друг от друга. На рис. 2 для примера показан случай спирального элемента, состоящего из одного витка. Область 3 на рис. 1 является диэлектрической ( f3 И ^3 – относительные диэлектрическая и магнитная проницаемости).

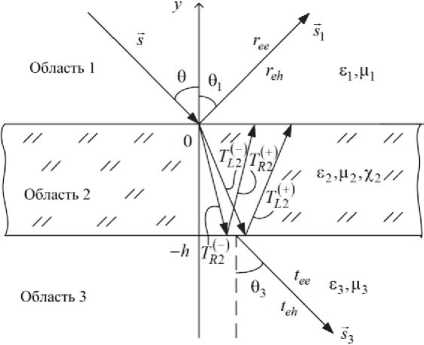
Рис. 1. Геометрия задачи

Задача состоит в получении соотношений для расчета коэффициентов отражения основной ( ^ее ) и кросс-поляризованной ( ^*eh ^ компонент поля в области 1, а также формул для коэффициентов прохождения основной ( t_ee ) и кросс-поляризованной ( /^ ) компонент поля в области 3. Здесь уместно отметить, что при взаимодействии падающего СВЧ излучения с киральной средой всегда возникает явление кроссполяризации [6-8], то есть в структуре отраженной и прошедшей волн возникают компоненты поля, ортогональные к компонентам падающей волны.

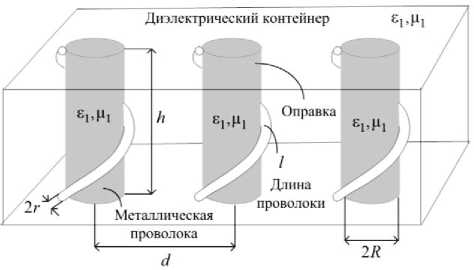
Рис. 2. Геометрия слоя кирального метаматериала

Киральная среда описывается в общем случае материальными уравнениями, одновременно связывающими между собой индукции и напряженности электрического и магнитного полей [6-7; 9]:

Ь = Ег^Ё*1%г^Н, В- цгН*гхг^Ё,

где верхние и нижние знаки соответствует спиральным элементам с право- и левовинтовыми закрутками, соответственно. Материальные уравнения (1) записаны в Гауссовой системе единиц.

Частотные зависимости параметров кираль-ного метаматериала определяются из следующих соотношений [10]:

1 (^Ю) ^{- 6}2с ⁺  2^ 2 ’

COq — О)

МЮН / 2 2'

где ^*2с – относительная диэлектрическая проницаемость контейнера; ^₀ – резонансная частота; A = 2 R – параметр, определяющий линейный размер спиральных включений, и р. – концентрация элементов; c – скорость света.

Для расчета резонансной частоты ^0 можно воспользоваться классическим методом. Спиральный элемент замещается эквивалентной низкочастотной схемой, содержащей емкость (сумма межвитковой и межэлементной емкостей, а также емкости тонкой металлической проволоки) и индуктивность проводника, закрученного в спираль. В частности, для емкости и индуктивности спирали получены следующие выражения:

2с

---^^--10

( ИЛ

181п — -1

£1сТС

h

'1ЛЩВ±г)

Л cos

7Г

т л^Н2Ъ = цг---—

Резонансная частота тонкопроволочного элемента в виде многовитковой спирали определяется по формуле Томсона:

б90 = i/ 4lc ,

где L и C определяются соотношениями (3). Нормальными волнами кирального метаматериала являются волны с право-(ПКП) и левокруговыми (ЛКП) поляризациями, обладающие различными постоянными распространения [6-9]:

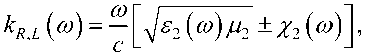
где зависимости ^2(®) И /2(®) определяются дисперсионными соотношениями (2) с учетом выражения для резонансной частоты (4).

На рис. 3 приведен типичный вид частотных зависимостей действительных частей постоянных распространения нормальных волн ^R L исследуемого кирального метаматериала. Из рис. 3 видно, что волны с право- и левокруговыми поляризациями испытывают явление бифуркации дисперсионных характеристик, причем степень дуплетного расщепления значительно выше вблизи резонансной частоты.

Кроме того, можно отметить, что на частотах ниже резонансной фазовая скорость у волны ЛКП больше, чем у ПКП, а выше резонансной частоты – характер изменяется на противоположный. При расчете считалось, что метаматериал образован спиралями с закрутками по часовой стрелке. Расчет был выполнен при следующих значениях геометрических размеров структуры: R = 0,01 м; N = 3; h = 0.05 м; d = 0,05 м.

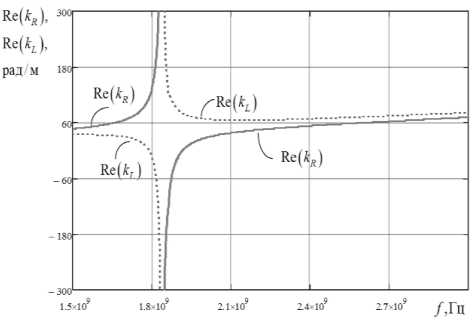
Рис. 3. Дисперсионные характеристики нормальных волн в метаматериале

На следующем этапе решения задачи методом частичных областей решалась задача об определении неизвестных коэффициентов отражения и прохождения для метаматериала на основе многовитковых тонкопроволочных спиралей. Электромагнитное поле в киральном слое опре- делялось из системы двух связанных дифференциальных уравнений второго порядка [8]:

V Ё + к^ ^₂/^2 ⁺ Z2 ) ^ ^— 2^z^o MiX^H = 0;

V²H + ^² (зд _{+ z}²) н + Хчх.Ё = о, (6)

где к₀ = со/с – волновое число для плоской однородной волны в вакууме.

Система уравнений (6) при помощи стандартного представления [6-7]

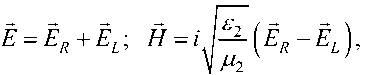
где Er – напряженность электрического поля волны ПКП; Er – напряженность электрического поля волны ЛКП была сведена к двум однородным уравнениям Гельмгольца для волн ПКП и ЛКП в киральной среде:

т tkniEni = О                (8)

где волновые числа для волн ПКП и ЛКП в безграничной киральной среде, определяемые соотношениями (5).

Из решения уравнений (8) с использованием представлений (7) для продольных составляющих векторов поля в киральном слое были получены следующие выражения [8]:

^(²) _ j^-t^'M^) ^jW^Sr,^ _|_

■¥Т^ечкъ ^L ,k>) + Т^Ёкь ^L ,?>) *

H^ = —

T^ p-ikR^R^ .T^ikR^R,?^ _

1R e             e

—Т^ечкь ^L ’k>) — T^eikL ^L ^ ’

где ^,1={8т^_£,-со8^_£} – единичные вектора, вдоль которых распространяются преломленные волны; Sr1=^0_rl,cos6_r^ – единичные вектора, вдоль которых распространяются волны, отраженные от области 3; Or L – углы преломления волн ПКП и ЛКП, соответственно; n^ = 7^2/^ – импеданс кирального метаматериала; ’ ^и Tl ^} – коэффициенты прохождения (по полю) волн ПКП и ЛКП в область 2; Tj⁺⁾ и 2^ – коэффициенты отражения (по полю) волн ПКП и ЛКП от области 3 в ки-ральный слой.

Явные выражения для всех тангенциальных составляющих векторов E^v ’ и H в кираль-ной среде приведены в [8].

Для случая падения плоской электромагнитной волны с перпендикулярной поляризацией для составляющих поля в области 1 справедливы следующие выражения:

z ^ (?^)

" ” ^ 6 +

COS^ iki(sr,r\ ее (1)                 ’ nz ~ rehe       ’

E^=-r_ehT]^W cos6>e"^,41(J-^?)

где s_r = (sin 0, cos 0 } – единичный вектор, определяющий направление распространения отраженной волны; ^ee – коэффициент отражения (по полю) основной компоненты; ^eh – коэффициент отражения (по полю) к росс -поляризованной компоненты; к = ^4^ – волновое число для плоской однородной волны в области 1. При решении задачи предполагается, что на киральный слой падает волна с единичной амплитудой напряженности электрического поля; 4^=EkEi – импеданс области 1.

Для составляющих векторов электромагнитного поля в области 3 с учетом кросс-поляризации можно записать следующие выражения:

f(³)-/ ^-^3(^7).

^z     leee          •> nz ~lehe       •>

ET =кьП^ cos^e

„(3) = COS x ee ,7(3) e

где s3 ={sin^3,-cos<93} – единичный вектор, определяющий направление распространения прошедшей волны; t – коэффициент прохождения (по полю) основной компоненты; ^eh – коэффициент прохождения (по полю) кросс-поляризованной компоненты; П^=л[Е/ёз – импеданс области 3; ^3 “ ^0 л/^з/^З – волновое число для плоской однородной волны в области 3.

На последнем этапе решения задачи были использованы граничные условия при у = 0и y = -h вида

^¹⁾(y = 0) = E<²⁾(y = 0); Н^у = ^ = Н®(у = оу, E^\y = -h) = E^(y = -h);

H^(y = -h) = H^(y = -hy

В результате подстановки (9)-(11) в граничные условия (12) относительно неизвестных коэффициентов отражения и прохождения получаем неоднородную систему линейных алгебраических уравнений вида:

АТ = Р,

где А – квадратная матрица размером 8×8, явный вид элементов которой в статье не приводится в силу их громоздкости;

т=К ^ Е' ту ту ту 1„ <„,]

Р = [о -1 cos^/^ О О О 0 о].

Коэффициенты матрицы А определяются геометрическими параметрами контейнера и спиральных элементов; материальными параметрами кирального слоя и областей 1 и 3, а также учитывают дисперсию ^₂(®) ^и Z₂(®) и, как следствие, форму включений. Аналогичным образом рассматривается случай падения волны с параллельной поляризацией, и решение задачи сводится к СЛАУ типа (13) с другими коэффициентами матрицы А и вектор-столбцом Р .

Анализ численных результатов

При анализе численных характеристик основной интерес представлял расчет частотных зависимостей отраженной (101g|ree и loigW ) и прошедшей (ioigM и ю igk„,l ) мощностей в дБ. Контейнер моделировался на основе пенополистирола С-35 с относительной диэлектрической проницаемостью f = 1,5.

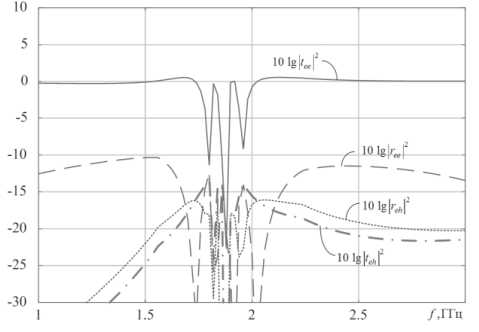
Рис. 4. Частотные зависимости отраженной и прошедшей мощности в диапазоне от 1 до 3 ГГц

На частоте 1,88 ГГц наблюдаются условия для наилучшей концентрации энергии падающего излучения, так как уровни прошедшей мощности, основной и кросс-поляризованной компонент поля имеют близко расположенные по частоте локальные минимумы (уровни ослабления прошедших мощностей основного и кросс-поляри-зованного поля более 20 дБ). Суммарное ослабление мощности падающего излучения в прямом и обратном направлениях по основной компоненте поля составляет около 43 дБ. По сути, на указанной частоте структура является защитным покрытием.

Из рис. 4 также видно, что вблизи частоты 1,88 ГГц на характеристике наблюдаются резонансные минимумы коэффициентов прохождения и отражения основной компоненты. В связи с тем, что потери в среде-контейнере отсутствуют, а потери на тепло в тонкой проволоке малы, можно утверждать, что падающая мощность преобразуется в энергию поверхностных волн. Подробный анализ данного явления проводится в [5] для случая метаматериала на основе элементов Телледжена, то есть разомкнутых колец с выступающими прямолинейными концами.

На других частотах метаструктура является полностью прозрачной, и падающее излучение через нее проходит практически без ослабления (вблизи 0 дБ). Таким образом, рассматриваемую структуру можно трактовать как частотно-селективный концентратор СВЧ энергии в районе частоты 1,88 ГГц.

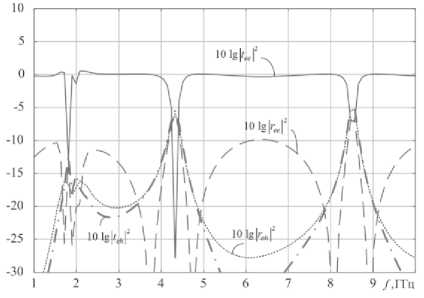
Рис. 5. Частотные зависимости отраженной и прошедшей мощности в диапазоне от 1 до 10 ГГц

На рис. 5 представлены частотные зависимости отраженной и прошедшей мощностей поля в диапазоне от 1 до 10 ГГц. Значения геометрических и физических параметров задачи аналогичны характеристикам на рис. 4. Как видно из рис. 5, ослабление прошедшей мощности основной компоненты имеет резонансы не только на основной частоте 1,88 ГГц, но и на частотах около 4,3 ГГц и 8,5 ГГц. На этих частотах происходит значительная кросс-поляризация поля и коэффициенты отражения и прохождения кросс-поляри-зованной компоненты имеют максимумы, однако и в данном случае часть энергии поля падающей волны переходит в энергию поверхностных волн, но более меньшая, чем на основной резонансной частоте. На всех других частотах метаструктура является прозрачной для СВЧ-излучения.

Таким образом, предлагаемый вариант метаструктуры выполняет функции многочастотного концентратора СВЧ-энергии, что позволяет, при подборе геометрических размеров контейнера и спиралей использовать ее для концентрации, например излучения от антенн GSM и WiFi одновременно. В результате проведенных расчетов доказано, что исследуемая метаструктура по свойствам является эквивалентной естественному кристаллу (или искусственной брэгговской решетке) в оптическом диапазоне, а именно частоты резонансных минимумов ослабления прошедшей мощности основной компоненты поля вычисляются из условия Вульфа-Брэгга с учетом преломления электронных волн в кристалле [11]:

2d ^^^ - zf ) ^{_ c}°s² # = ^Л (14)

где v – порядок резонанса; к – длина волны;

• 9 – угол падения волны.

Используя (14), несложно записать выражение для резонансных частот метаструктуры, на которых происходит преобразование нормально падающего электромагнитного излучения в поверхностные волны:

cv

Jv ” U        Э \     7⁼

2d JI e-ja^ - z£ I - cos" 0

(у = 1,2,3,....).

Можно отметить две возможности применения исследуемого метаматериала вблизи резонансной частоты:

• -    частотно-селективный концентратор СВЧ-энергии, проводящий преобразование нормально падающей электромагнитной энергии в поверхностное (азимутальное) рассеяние;

• -    частотно-селективный защитный экран, непрозрачный для излучения вблизи основной резонансной частоты.

Заключение

Сформулируем основные выводы по результатам работы.

• 1.    Концентратор электромагнитной энергии на основе киральной метаструктуры вблизи заранее заданной частоты позволяет выполнять преобразование нормального падающего потока электромагнитной энергии в азимутальное рассеяние.

• 2.    Концентратор электромагнитной энергии на основе киральной метаструктуры вблизи заранее заданной основной резонансной частоты позволяет выполнять функции частотно-селективного защитного экрана.

• 3.    В работе подобраны геометрические размеры концентратора, при которых киральный метаматериал обладает возможностью «захватывать» СВЧ-излучение вблизи частоты 1,88 ГГц.

• 4.    Теоретически предсказана возможность дискретно-многочастотной концентрации падающей СВЧ-энергии при помощи киральной метаструктуры на ряде резонансных частот.

• 5.    Доказано, что частоты, на которых метаматериал концентрирует СВЧ-энергии, подчиняются соотношению, аналогичному условию Вульфа-Брэгга для кристаллической среды.