Кислотно-основные свойства поверхности оксидных материалов

Кислотно-основные свойства различных материалов давно и интенсивно изучаются, главным образом, в связи с их адсорбционными и каталитическими свойствами [1 – 4].

В частности, кислотно-основной характер активных центров на поверхности оксидных минералов во многом определяет их поведение в природной среде, взаимодействие с поровым раствором, является причиной образования геохимических барьеров и существенно связан с комплемен-тарностью поверхности в отношении к простейшим биомолекулам в концепции генобиоза [5].

Наиболее распространенным методом изучения кислотно-основных свойств (в рамках концепции Бренстеда) оксидных материалов является потенциометрическое титрование их суспензий в водной среде. Использование неводных растворителей перспективно в отношении изучения кислотноосновных свойств в рамках концепции Льюиса. Обычно титрование проводится из кислой области в щелочную (и наоборот) добавлением к суспензии, содержащей известную концентрацию свободной сильной кислоты cHA , последовательных порций сильной щелочи с концентрацией c и измере-

BOH

нием при этом рН раствора.

Кислотно-основные свойства изучаемого материала удобно охарактеризовать соответствующим рК-спектром [2, 3], представляющим собой гистограмму, площадь отдельных полос которой равна вероятности того, что характеризующая данный кислотно-основной центр величина рK i лежит в интервале между pK i и pK i + A pK. Расчет рК-спектров проводится на основании экспериментальной кривой титрования, выражающей зависимость Гиббсо-вой адсорбции ионов водорода на изучаемой поверхности от рН раствора (в расчете на 1 г изучаемого образца):

c u д V o — c roh V — [H ] " ( V o + V )         i \

Г н (pH) = ^HA 0 —BOH--------- 0----, ммоль/г. (1)

m

Здесь V0 – объем суспензии, взятой для титрования, концентрация одноосновной сильной кислоты в которой равна cHA , V – объем добавлен- ной щелочи с концентрацией cBOH , m – масса твердой фазы суспензии (г) во взятом образце. Концентрация ионов водорода в уравнении (1) рассчитывается из рН раствора по уравнению [H + ] = 10 - pH.

Интерпретация кислотно-основных свойств оксидных материалов обычно проводится в рамках концепции Дэвиса – Джеймса – Лекки [1] на основе так называемых 2рК и 4рК- моделей.

В 2рК-модели предполагается, что заряд по- верхности появляется в результате ионизации поверхностных амфотерных групп ─SOH по следующим реакциям и описывается соответствующими им уравнениями закона действующих масс:

_{+                +}              [-SOH] • [H ⁺ ]

-SOH 2+ ^ -SOH + H⁺ ( K ), K =

^{1     1}     [-SOH + ]

₊                   [-SO^-] • [H ⁺ ]

-SOH ^ -SO^- + H⁺ ( K ,).   K, =            .

2      2 [-SOH]

Здесь индекс ─S используется для обозначения поверхности изучаемого образца. Константы равновесия K 1 и K2 характеризуют силу рассматриваемых кислотно-основных центров и постоянны при проведении эксперимента в условиях постоянной концентрации фонового электролита.

В кислой области (рН<=6) наблюдается равновесие (2), а в щелочной (рН>=9) – равновесие (3).

В тех случаях, когда константы K 1 и K 2

оказываются зависящими от концентрации фонового электролита, вместо модели 2рК используется модель 4рК. 2рК-модель – частный случай 4рК-модели, которая допускает возможность частичной нейтрализации поверхностного заряда ионами индифферентного электролита (например, NaCl), т.е. образованием на поверхности ионных пар:

_{+              +}                  [SOH] • [H ⁺ ] • [Cl^-]

SOH%Cl< > SOH+H + +Cl( K. ), K, =

^{3   3}      [SOH + Cl^-]

SOH+Na + ^ SO Na + +H + ( K 4 ), K 4 =

[SO^-Na ⁺ ] • [H ⁺ ] [SOH] • [Na ⁺ ] .

Очевидно, большие значения констант K 3 и

K 4 соответствуют специфической адсорбции катионов, а малые значения – специфической адсорбции анионов.

Вообще говоря, зависимость констант K 1 и

K 2 от концентрации фонового электролита можно объяснить не только образованием ионных пар по реакциям (4) и (5), но и изменением коэффициентов активности реагирующих ионов, как это обычно делается при изучении комплексообразования в растворах.

Решая теперь систему уравнений законов действующих масс для равновесий (2), (3), (4), (5) и уравнений, выражающих условие электронейтральности раствора:

[SOH 2 ⁺] + [H⁺] + [Na⁺] – [SO^-] – [Cl^-] = 0, условие баланса ионов Na⁺ и Cl^- в системе (считая, что в качестве фонового электролита используется NaCl):

[NaCl] = [Na+] + [SONa], и

[NaCl] + [HCl] = [Cl^-] + [SOH 2 Cl], получаем следующее уравнение для расчета величины F _H(pH) :

c - ^{[H ]}

Г_н (pH) = -HC      =

^H        B

( K ₃ / K 1 + [NaCl]) [H ⁺ ]² - K ₃ K ₄[NaCl]- K 2 K 3

( K 3 / K 1 + [NaCl]) [H ⁺ ]² + K 3 [H ⁺ ] + K 3 K 4[NaCl}^ K 2 K 3

При решении предполагалось, что [NaCl] = [Na⁺] = [Cl^-], что справедливо при достаточно малых количествах твердой фазы и сравнительно высоких концентрациях фонового электролита. На рис. 1 представлен график зависимости ^(pH) для случая, когда рК 1 = 3.2, рК 2 = 8.7, рК 3 = 4.0, рК 4 = 7.0 (анатаз [6]) и при различных концентрациях NaCl. C ростом концентрации фонового электролита кривая в данном случае смещается в сторону более меньших значений рН в области положительных величин r H(pH) и в сторону более высоких значений рН в области отрицательных значений ^(pH) .

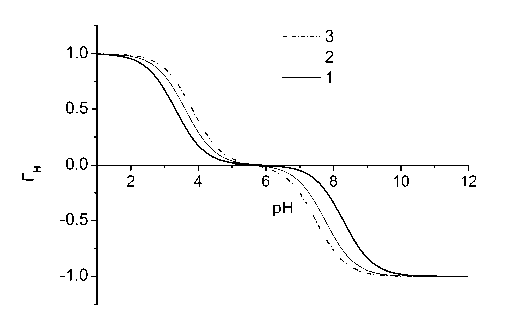
Рис. 1. Зависимость ^(pH) при различных концентрациях фонового электролита: 1 – 0.05 М, 2 – 0.25 М, 3 – 0.5 М NaCl.

Полученная зависимость ^(pH) может быть использована для построения соответствующего рК-спектра. Полная адсорбция ионов водорода на поверхности изучаемого сорбента, очевидно, равна:

N_ N_ I ^r H ^{( pH} ) +^Г 0 = 5^r H i = ^^r i     pH-pK. ■       ⁽⁷⁾

i i 1 + _w^{p p} 1

Суммирование в уравнении (7) проводится по всем ионам водорода или числу кислотно-основных центров N , находящихся на поверхности данного образца. Г , - полная обменная емкость i - го кислотно-основного центра, pK i – показатель константы диссоциации этого центра (отрицательный десятичный логарифм константы диссоциации). Г 0 — количество адсорбированных ионов водорода на изучаемой поверхности, не зависящее от рН раствора и соответствующее точке нулевого заряда протонов этой поверхности. Эту величину можно рассматривать как количество «не титруемых» в условиях проведения эксперимента ионов водорода, например, ионы водорода, входящие в состав OH-групп на поверхности изучаемого адсорбента, когда pK , ^- го . Величины Г н ( pH ) и Г ) могут быть как положительными, так и отрицательными в зависимости от положения разделяющей поверхности, которая обычно соответствует поверхности образца.

Сложность решения уравнения (7) относительно величин Г, обусловлена тем, что общее число N кислотно-основных центров заранее неизвестно.

Таким образом, каждое уравнение системы (7) линейно зависит от Г ) и N величин r i , а также нелинейно от N величин pK i . Общее число неизвестных равно 2 N +1. Для решения такой системы уравнений следует составить по меньшей мере 2 N +1 уравнений, что возможно, если экспериментальную кривую титрования аппроксимировать каким-либо сглаживающим сплайном и использовать этот сплайн для расчета величин Г н ( pH ) при заданных значениях рН. Очевидно, стандартный метод наименьших квадратов в данном случае не подходит, тем более, что заранее известно, что величины Г, положительны.

Поскольку величины Г i являются однозначными функциями дискретного множества величин pK i , уравнение (7) можно переписать в виде: ^rH ⁽ p^{H )} = -^r₀ + N HpK ’- 5 ⁽ pK - pK i )-- ^{- pK}     .

I = 1 -го                      1 + 10p ^p

Здесь d ( pK - pK i ) - дельта-функция. Число уравнений вида (8) равно числу величин Г н ( pH ) , соответствующих дискретным значениям рН и определяемых с помощью выше упомянутого сплайна.

Если значения величин pKi лежат в интер- вале pKmin < pKi < pKmax, то уравнение (8) можно представить в виде:

Гн^-Г )

N ^pKmax

+ Z j r(pK)- 5(pK-pp)-i=1pK ■ min dpK i+iopH"pK.

Разбивая область интегрирования на интервалы шириной ApK, представим каждый интеграл уравнения (9) в виде суммы: pKmax

HK)* - pK, )-  »pK = pKmin                         1 + 10               ,    (10)

l pK y +^A pK

= Z   j г⁽ pK ) -6 ( pK - pK , ) .     > pK

J = 0 pK ,.                            ^{1 + 10}

где l = ( pKmax - pKmin ) / A pK-1 - равно числу интервалов шириной A pK . В результате уравнение (10) принимает вид:

Г ( pH ) = -f 0 +

Nl

+ z z i = 1 j = 0

= -Г0 + lN

+z z j=0 i=1

pK j +^A pK

J r ( pK ) .S ( pK - pK , ) . —L pK _j

^PK j +^{A pK}                        J V

J* ) -8⁽ pK - pK , ) - 1 _{+ 1}" pH - pK .

pK _j

Выполняя интегрирование и суммирование по i в последнем уравнении, получаем:

^Г н ⁽ p^H ) = ^-Г 0 ^{+ z a}j , J =^{0 J}

где а равно либо 0, либо Г ,-- H - p ,

1 + 10p p i если pKi попадает в интервал pKmin + jApK < "K < pKmin + (j + 1)apK - в ре-mn           mn зультате чего pKi можно аппроксимировать вели- чиной      pK j = pKmin + jApK ,      положив

{Г, | i = 1...N} ■ {Гj | j = 0.J}. Окончательно урав- нение (11) принимает вид:

l 1

г_н ( pH ) = г, - ( - 1 ) +У г, ----———,

H\r /    0 \             j 1 + 10"H -(pKmin+ jApK) , где

^г , =1

_; >  0 , если

_pKmin + jApK < "Ki < pKmin + (j + 1)ApK.

Таким образом, нахождение набора чисел

{ Г j\ j = 0.. l } ,    включающего набор чисел

{Г, | i = 1...N}, можно выполнить обычным методом наименьших квадратов с ограничением на положительные значения корней (алгоритм NNLS [7]), если предполагается, что Г, и Г0 > 0, на основе экспе- риментальной зависимости Гн (pH). Неопределенность найденных таким образом величин pKi характеризуется шагом ApK изменения pK и может быть снижена уменьшением этого шага и, соответственно, возрастанием числа членов l суммы по j в уравнении (12), если экспериментальную зависимость Гн (pH) интерполировать соответствующим сплайном. Величину ApK можно рассматривать как доверительный интервал для найденной таким образом величины pKi . Данная задача относится к числу некорректных задач [8], и при ее решении необходимо принимать во внимание погрешность экспериментальных данных.

Результаты решения задачи удобно представлять в виде гистограммы зависимости чисел l qj =Гj £ Г от соответствующих им величин J Л i=0

pK _j . Число полос на такой гистограмме будет равно числу индивидуальных равновесий, описывающих изучаемую диаграмму состав – свойство. Сама гистограмма может быть названа рК-спектром изучаемой системы. Надежный рК-спектр, очевидно, может быть получен лишь при минимально возможной погрешности экспериментальных данных. В данном случае возникает своеобразный принцип неопределенности , согласно которому неопределенность рК-спектра является следствием неопределенности ошибки эксперимента.

На рис. 2 представлен рK-спектр (для A pK=0.1), построенный по данным рис. 1, из которого видно, что найденные этим методом величины рК i близки к заданным при построении рис. 1. По оси ординат здесь отложена относительная мольная доля соответствующего кислотно-основного центра от общего их числа ( q ).

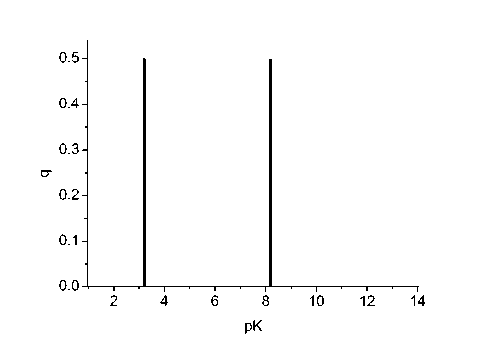
Рис. 2. рК-спектр анатаза при [NaCl]=0.

Уравнение (6) перепишем в виде:

Г _H(pH) =

[H ⁺ ]² - K‘K 2

[H ⁺ ]² + K ‘ [H ⁺ ] + K 1 K 2

в котором штрихованные константы соответствуют величинам рК i , получаемым при использовании фонового электролита:

^K 1 =

^K 1 • ^K 3     _

K 3 + K 1[NaCl] ’

и

K 2 = K 4[NaCl] + K 2 .

При этом K1 и K 2 соответствуют, очевидно, предельным значениям штрихованных констант при нулевой концентрации фонового электролита. Если константы K1 и K2 найдены в условиях очень низкой (практически нулевой) концентрации фонового электролита, то уравнения (14) и (15) позволяют определить константы K3 и K4 при условии, что штрихованные константы определены из рК-спектров, соответствующих заданной концентрации фонового электролита.

Из полученных уравнений следует, что при увеличении концентрации фонового электролита полоса, соответствующая величине pK, должна сдвигаться в сторону более высоких значений, а полоса, соответствующая величине pK^, в сторону более низких значений. Положение точки нулевого заряда протонов pznpc (Гн (pH) = 0) определяется выражением:

pznpc = I (pK 1 + pK^) =

^(pK1 + pK2) - ^g

K 3( K 2 + K 4[NaCl]) ’ K 2( K 3 + K 1[NaCl])

и в пределе очень большой концентрации фоново- го электролита стремится к величине

2"(pKg + pK4). При специфической адсорбции катионов фона на изучаемой поверхности точка нулевого зарядов протонов сдвигается в область более низких значений рН, а при специфической адсорбции анионов – в сторону более высоких значений рН. При достаточно высоком сродстве поверхности к присутствующим в растворе катионам можно ожидать, что величина Гн (pH) во всей изучаемой области рН окажется отрицательной.