К.Э.Циолковский - П.Г.Кузнецов - Л.Ларуш: аналогии и подобие в работах ученых-энциклопедистов

В год 155-летия Константина Эдуардовича Циолковского подчеркнем, что для его работ характерно многообразие интересов, по сути общесистемность. Это отмечал А.Е. Ферсман [1, с. 425]. Всю жизнь Циолковского занимала мысль о подобии, как аналогиях внешне различных явлений, позволяющих по частному делать выводы о целом по законам преобразования. Это нашло выражение в работе «Механика в биологии. Подобие организмов и уклонение от него» [2], начатой еще в 1882 г., где разрабатывается теория единого описания сложных биологических систем на основе применения количественных законов механики [3]. Вся научная и общественная деятельность характеризует К.Э. Циолковского как ученого-энциклопедиста, наследие которого не освоено, требует изучения и развития.

В области управления обществом идеи аналогий и подобия развивают выдающиеся ученые-энциклопедисты современности Линдон Ларуш и Побиск Георгиевич Кузнецов. Их личная встреча состоялась в 1994 г. на семинаре в Вычислительном центре РАН. Вел семинар Револий Михайлович Суслов. Взгляды двух ученых на проблемы роста и развития общества, их умение видеть сходное в различном, дополняют друг друга [4].

П.Г. Кузнецов ввел понятие «миллионник», т.е. расчеты потребностей, включая площади посевов, обеспечение продуктами питания, одеждой, жилищем, теплом, транспортом – которые необходимы для жизнеобеспечения миллиона людей в течение года.

На этом понятии была построена программа «Губернатор», которая рассматривала, сколько и чего производит область, что будет производить, что может вывозить, что должна ввозить. На что тратить средства, предназначенные для инвестиций, чтобы увеличить потребление, снизить ввоз, увеличить вывоз.

Л. Ларуш ввел и активно использует понятие количества людей, которых прокормит квадратный километр поверхности земли.

Это количество людей меняется, и будет меняться по мере роста потребностей людей и роста совершенства технологий. Рост количества людей, которых кормит квадратный километр поверхности земли, является измеримой характеристикой качества научнотехнического прогресса.

Для реализации этих идей в реальных условиях необходимы расчеты больших объемов информации на основе математических сетевых моделей, которые используют аналогии и подобие между биологическими, экономическими системами и техническими системами. Для технических и физических систем разработаны методы моделирования, расчета, анализа. Но можно ли их применять в экономике, биологии? Есть принципиальные различия между живыми и неживыми системами по отношению к свободной энергии.

Живые системы увеличивают свободную энергию в процессе своей деятельности.

Неживые системы теряют свободную энергию в процессе своей деятельности.

П.Г. Кузнецов на лекциях начинал с того, что приводил пример мужика, который работает и добывает энергии для себя и семьи. То есть, создает энергии больше, чем расходует. Потребляет 2400 Ккал, а создает не менее 10000 Ккал.

Проблема моделирования с применением подобия и аналогий состоит в том, как можно представить механизм увеличения свободной энергии в живых системах с помощью неживых систем. Другими словами – можно ли считать, что мир устроен для тех и других систем одинаково, и на них действуют одни и те же законы физики .

Или в мире, во Вселенной есть еще и специальные законы физики для живых систем, специальные виды энергии, которые управляют их поведением, обеспечивая им свойства, отличающие их от неживых систем .

Т.е. надо ли считать, что существует высшая сила, которая дает живым системам новые свойства. И, по-видимому, подчиняется таким законам и силам, которые нам неизвестны. Во всяком случае, они не могут быть объяснены нашей наукой. Библия учит, что Бог вдохнул жизнь в Адама. А до этого он был куском глины. Его дыхание началось с вдоха. Это одна точка зрения на дыхание и поведение живого.

Фильм «Опасный спуск с Эвереста» начинается словами. «Учитель сказал: прежде, чем вдохнуть чистый воздух Эвереста, ты должен выдохнуть грязь, которая накопилась в тебе в городе. И тогда я понял, что дыхание начинается с выдоха». Это другая точка зрения на дыхание и поведение живого.

Или достаточно тех законов, которые нам известны, чтобы создать искусственную живую систему. Тогда представим себе, что с накоплением сложности неживых систем, возникнет механизм накопления энергии. Это получается согласно принципу Паули для биологии. И возникает саморазвитие путем размножения.

Принцип Паули (принцип запрета) — один из фундаментальных принципов квантовой механики, согласно которому два и более тождественных фермиона не могут одновременно находиться в одном квантовом состоянии. Этот принцип утверждает, что в пределах одной квантовой системы в данном квантовом состоянии может находиться только одна частица, состояние другой должно отличаться хотя бы одним квантовым числом. Иначе можно сказать, что в одном месте пространства, в одно время может находиться одно тело, другие тела сюда поместить нельзя.

Следствием принципа является постепенное заполнение электронных оболочек в структуре атома. Само существование оболочек является структурным свойством пространства, из которого следует разнообразие химических элементов и их соединений. Принцип Паули запрещает электронам принимать одинаковые квантовые состояния. По этой причине электроны не могут быть в одном квантовом состоянии с наименьшей энергией, а заполняют последовательно квантовые состояния оболочки, с наименьшей (свободной в данный момент) суммарной энергией.

Это свойство заполнения свободного места, и запрета заполнять занятое место, действует и для людей. Известно, что из двух близнецов, во всем одинаковых, один обладает характером лидера (альфа), а другой – ведомого (омега). По этой причине, как и в атоме, в обществе начинают заполняться наиболее низкие уровни по интеллектуальному развитию. Когда они заполнены, возникают личности с более высоким интеллектом, а по мере их заполнения возникают личности с все более высоким творческим потенциалом. Таким образом, чтобы создать гения, надо сначала создать много не гениев. Так проявляет себя принцип Паули для биологии [5].

Уже предпринимались попытки создания сетевых конструкций с электромагнитным возбуждением, а также более сложными типами волн, чтобы получить объект, обладающий свойствами живого организма. В частности, Г. Крон (американский инженер венгерского происхождения, 1901–1968) писал в предисловии к переизданию в 1965 г. книги «Тензорный анализ сетей» про возможности полиэдральных сетевых моделей к самоорганизации, т.е. физической реализации свойств искусственного мозга.

«Погружением двухфазной (первичной и двойственной) полиэдральной структуры в n-мерную область, наполненную неподвижной или движущейся плазмой, можно распространять через полиэдр магнитогидродинамические, ионные, химические и еще более общие волны. Каждый р -симплекс и его двойственная (п —р)-ячейка вместе становятся единой, двухфазной, «обобщенной» вращающейся электрической машиной. Так, можно добавить к электромагнитным параметрам большое число механических, термодинамических и других параметров, которые удовлетворяют как уравнениям Лагранжа, так и уравнениям термодинамики необратимых процессов. Все они образуют самосогласованную структуру, которая, как доказывается уже фактически найденными численными примерами, обладает способностью к самоорганизации» [6, с. 34-35] . Ранее Крон опубликовал ряд статей по теории полиэдральных, т.е. многомерных сетей, и результаты опытов с ними. Таким образом, Крон утверждал, что полиэдральные волновые автоматы обладают свойствами самоорганизации в смысле изменения их параметров в ответ на внешние воздействия.

Затем в Англии опыты с полиэдральными сетями и волновым автоматом Крона пытался повторить Дж. Линн с сотрудниками. Им удалось построить полиэдральную структуру сети с волновым возбуждением, однако не смогли получить свойств самоорганизации в такой сети. Монография с попытками обосновать теорию полиэдральных сетей была опубликована в 1970 г. [8]. Статья Линна и Рассела «Волновой автомат Крона» была опубликована в сборнике по графам связей в 1974 году [7]. Этот сборник в качестве эпиграфа начинается цитатой из книги Г.Крона «Тензоры для цепей», опубликованной в 1942 г. «Удивительно, как мало существует первичных типов элементов, образующих строительные блоки огромного разнообразия технических структур. … Огромное разнообразие структур отличается только способом соединений, … а многообразие теорий только типом рассматриваемой гипотетической системы отсчета».

Аналогии и подобие в структуре

Чтобы начать движение по пути конструирования живого из неживого, надо сначала построить наиболее простую модель. Т.е. такую искусственную техническую систему, которая бы обладала свойствами, похожими на свойства живой системы. Такой моделью может служить электрическая цепь, с ее свойствами двойственности структуры, которая бы увеличивала потоки энергии в ответ на внешнее воздействие. Это и есть один из признаков, свойств живой системы.

Оказывается, что свойства двойственности электрической цепи позволяют создать конструкцию, которая работает на увеличение энергии. Это сетевая модель в виде электрической цепи, представляющая производство продукции в задаче межотраслевого баланса. Воздействием является спрос, моделируемый источников тока (внешнее, узловое воздействие). В ответ модель генерирует в дополнение к внешнему воздействию источники напряжения (контурное, внутреннее воздействие). Комбинация контурных и узловых токов создает на ветвях сети больше мощности, чем от исходных внешних воздействий, т.е. приводит к увеличению потоков энергии.

Процессы, протекающие в такой сетевой модели, как электрическая цепь, считаются известными. Это распространение электрического тока через сеть проводников под действием источников напряжения и тока. В широких пределах этот процесс описывает закон Ома, а токи в узлах и напряжения в контурах подчиняются законам Кирхгофа.

Новым в такой модели являются свойства двойственности структуры связи элементов-ветвей. Эти свойства автор открыл при попытке понять, в чем суть споров по поводу инварианта мощности. Начиная с 30-тых гг. прошлого века имели место дискуссии об основах тензорного анализа сетей, который разработал Г. Крон. Создавая тензорный анализ сетей Крон предложил постулат об инвариантности мощности. [6]. Он утверждал, что при соединении отдельных ветвей в связанную сеть, рассеиваемая мощность не меняется, на том основании, что не меняется мощность источников. Это необходимо для получения формулы преобразования импеданса (комплексного сопротивления) при соединении отдельных ветвей в цепь (сеть). Постулат стал предметом научной критики, (а порой и дискуссии, выходящей за пределы науки) на протяжении десятилетий. Спектр мнений о методе Крона автор опубликовал в монографии «Тензорная методология в теории систем» в 1985 году [10].

Задача проведенного автором исследования состояла в поиске закономерности изменения рассеиваемой в электрической цепи мощности в зависимости от изменения соединения ветвей цепи, т.е. в зависимости от изменения структуры. В результате исследования, которое состояло в проведении вычислительных экспериментов по расчету электрических цепей, обнаружено постоянство рассеиваемой мощности в электрических цепях с данной и двойственной структурой при любых способах соединения ветвей, сохраняющих их двойственность . Таким образом, среди характеристик электрической цепи появилась двойственность структуры цепей, и связанный с ней инвариант . Таким образом, мощность инвариантна при изменении соединений, но в сумме двух двойственных цепей. Такой инвариант связывает матрицы преобразования двойственных сетей при изменении структуры:

C (C t C)^-1 C t + A (A t A)^-1 A t = I.

где C – матрица преобразования путей в данной сети; A – матрица преобразования путей в двойственной сети; I – единичная матрица.

Инвариант, который выражает данную закономерность, позволяет преобразовать решения при любом изменении структуры сетей (соединения, разъединения, разделение на части или соединение из частей целого). Эта закономерность связывает процессы и структуру в сетях, сетевых моделях сложных систем в их взаимодействии и взаимном изменении.

Материальные характеристики ветвей можно представить как веса. Если ветвям сети приписаны веса (собственные и взаимные), выражаемые матрицей Z (Z = Y^-1 ) , то указанное инвариантное соотношение для замкнутых путей примет вид:

(Z)^-1 = Y = ^mC t ( ^mC Z ^mC)^{-1 m}C + Y ^jA t (^jA Y ^jA t )^{-1 j}A Y.

Если на сеть наложен вектор (воздействие), то его компоненты принимают значения в базисе замкнутых (внутреннее воздействие) или разомкнутых (внешнее воздействие) путей. В данном случае инвариант – это постоянство длины вектора: часть вектора в одной сети, часть в двойственной сети, но их сумма постоянна и не зависит от изменения соединений. Для вектора потока энергии, заданного в замкнутых путях, формула преобразования контравариантных компонент при изменении структуры имеет вид:

md0α = mdαс + mdαс = mdα mCα`α + mdα jAα`α Yαβ = (mCα`α)t mdα + (jAα`α)t Yαβ mdβ, где mdсα и mdсα – компоненты вектора в двойственных сетях. Нельзя получить компоненты вектора md для связанной сети по их значениям в свободных ветвях, поскольку в связанных ветвях они распадаются на совокупность компонент вектора потока энергии в двойственных сетях и только в сумме дают компоненты полного вектора.

Для разомкнутых путей данные инвариантные соотношения имеют такой же вид, а преобразования такой же смысл, но при двойственной замене величин.

Технические и экономические системы похожи в том, что в них через соединенные элементы проходят потоки энергии. Совокупность связей элементов составляет структуру системы. Преобразование потоков энергии составляет суть процессов в системе. При математическом моделировании процессы должны быть представлены только в терминах измеримых величин, применение которых дает возможность экспериментально проверить результаты ( Кузнецов О.Л., Большаков Б.Е ., 2002) [11]. В указанной работе все системы реального мира делятся на равновесные и неравновесные системы. Равновесная система не может совершать внешней работы, поскольку все внешние «обобщенные силы» (потоки) уравновешены внутренними силами. Неравновесная система может совершать внешнюю работу, эволюционируя во времени, поскольку внешние потоки не уравновешены внутренними потоками.

В соответствии с данной классификацией, которая отражает реальную ситуацию в окружающем мире, системы делятся на три типа.

• 1.    Уменьшение свободной энергии и рост энтропии. Этому соответствуют системы с доминированием процессов рассеяния свободной энергии и приближения к равновесию.

• 2.    Увеличение свободной энергии и уменьшение энтропии. Это системы с доминированием процессов накопления свободной энергии и удаления от равновесия.

• 3.    Отсутствие изменений свободной энергии и энтропии. Это ситуация неустойчивого равновесия внешних и внутренних потоков^*.

С точки зрения данной классификации, можно разделить системы на неживые, которые относятся к первому типу, и живые, которые относятся ко второму типу.

Технические системы, как и вообще неживые системы, рассеивают потоки энергии, совершая работу в процессе преобразования поступающей в них энергии (воздействий) с коэффициентом полезного действия (кпд) меньше единицы. Экономические системы, как и вообще живые системы, не только рассеивают потоки энергии, но и накапливают энергию; в этом суть размножения и воспроизводства. При этом их видимый кпд оказывается больше единицы.

В.И.Вернадский в 1935 году писал: «Природные процессы живого вещества в их отражении в биосфере увеличивают свободную энергию биосферы (первый биогеохимический принцип). Все природные процессы в области естественных косных тел – за исключением явлений радиоактивности – уменьшают свободную энергию среды (биосферы)».

Рассмотрим, сколько есть видов двойственности структуры и видов воздействий и откликов в цепи, и сети, как ее абстрактном представлении, для построения сетевой модели, которая будет обладать свойствами живой системы.

Существуют пути двух видов: замкнутые и разомкнутые, открытые. Они превращаются друг в друга при соединении и разъединении ветвей в сети.

Если первоначально все элементы-ветви в сети замкнуты, разомкнутых путей нет, то при соединении элементов друг с другом часть путей будет разомкнута, число разомкнутых путей возрастет с нуля до некоторой величины, и на столько же уменьшится число замкнутых путей. В двойственной сети при этом первоначально все элементы-ветви разомкнуты, замкнутых путей нет, но при двойственном соединении элементов друг с другом часть путей будет замкнута, число замкнутых путей возрастет с нуля до некоторой величины, а число разомкнутых путей на столько же уменьшится. Количеству соединений в одной сети соответствует количество разъединений в двойственной сети.

Таблица 1

	Свободные ветви, т.е. не имеют соединений друг с другом	Изменения структуры	Соединенные ветви, т.е. на сеть и двойственную сеть наложены связи
Сеть	Все пути замкнутые	Замкнутые пути размыкаются, появляются разомкнутые пути	Сумма замкнутых и разомкнутых путей равна количеству ветвей
Двойственная сеть	Все пути разомкнутые	Разомкнутые пути замыкаются, появляются замкнутые пути	Сумма замкнутых и разомкнутых путей равна количеству ветвей
Полная сеть из двух двойственных сетей	Сумма замкнутых и разомкнутых путей в двух сетях равна числу элементов в двух сетях, т.е. двойному количеству ветвей	Количество замыкаемых путей в сети равно количеству размыкаемых путей в двойственной сети, и наоборот	Сумма замкнутых путей в двух сетях и сумма разомкнутых путей в двух сетях постоянные и равны количеству ветвей

Главный показатель изменения структуры одномерной сети состоит в изменении количества узлов (вершин графа). Изменяемые при этом пути (замыкания и разъединения) составляют матрицу изменения путей, на которой построены алгоритмы расчета по частям (обобщенная диакоптика).

Другой тип двойственности представляют собой характеристики потока энергии, протекающего в структуре; величины воздействия и отклика по способу их измерения делятся на два типа:

• •   величины, которые измеряют в одной точке (например, электрический ток), –

продольные величины;

• •    величины, которые измеряют как разность значений в двух пространственно различных точках, (например, электрическое напряжение измеряется как разность значений потенциала между эквипотенциальными поверхностями); – поперечные величины.

Воздействие и отклик, составляющие вектор потока энергии, всегда представлены парой: продольной величиной и поперечной величиной.

Физические величины воздействий и откликов, характеризующие потоки энергии, по типу измерения (продольные и поперечные) для открытых и закрытых систем меняются местами. Базисом для процессов в открытой системе являются разомкнутые пути. Базисом для процессов в закрытой системе являются замкнутые пути. Отношения между этими понятиями представлены в таблице 2.

Таблица 2

	Воздействие	Отклик
Закрытая система, базис определяют замкнутые пути	Поперечная величина	Продольная величина
Открытая система, базис – разомкнутые пути	Продольная величина	Поперечная величина

Например, для электрической цепи. Источники напряжения (поперечная величина) расположены в ветвях самой цепи, являются внутренними воздействиями. Отклики, токи (продольная величина) возникают в контурах, т.е. в замкнутых путях. Этому соответствует контурный метод расчета. Проводим расчет контурных токов (в независимых, базисных контурах), по ним – токи в ветвях и падения напряжения на ветвях. Токи и напряжения на ветвях в совокупности и являются решением задачи, описывают процесс – поток электрической энергии в цепи.

Источники тока (продольная величина) являются внешними воздействиями, они расположены вне цепи и действуют через узлы входа и выхода. Отклики, напряжения (поперечная величина) возникают на парах узлов, т.е. в разомкнутых путях. Этому виду воздействия соответствует узловой метод расчета. Независимые, базисные пары узлов соответствуют разомкнутым (открытым) путям базиса в данном случае. Проводим расчет напряжений между узлами (начало и конец разомкнутого пути), по ним – падения напряжений на ветвях и токи в ветвях. Напряжения и токи на ветвях в совокупности и являются решением задачи, описывают процесс – поток электрической энергии в цепи. Используя рассмотренные типы двойственности структуры и процессов в структуре, построим сетевую модель для задачи баланса потоков продуктов. Эти потоки могут протекать в системе хозяйства, или в живом организме, обеспечивая обмен веществ и поддержание жизнедеятельности.

Технология моделирования живой системы на примере экономики

План-спрос будем представлять в модели как вектор потока разомкнутых путей – воздействующий узловой ток, а потоки в отраслях, поставки и ресурсы – как отклики. Казалось бы, можно для представления использовать двойственный источник воздействия в замкнутых путях – источник напряжения. В двойственном смысле эти величины равноправны. Однако дело в том, что разомкнутые пути обеспечивают представление экономики как открытой системы. Спрос формируется вне рассматриваемой системы. Ресурсы также поступают извне, причем некоторые ресурсы могут представлять поставки со стороны тех отраслей, которые не вошли в рассматриваемую систему отраслей. Это обеспечивает определенную свободу в отношении выбора, – какие отрасли включать в конкретную сетевую модель, а какие считать «внешней средой». Связь открытой системы с внешней средой обеспечивают разомкнутые пути, и соответствующие им источники воздействия, формирующие потоки в сети.

При использовании сетевых аналогий необходимо учесть разницу между техникой и экономикой. Отличие токов и потоков продуктов выражено упомянутой выше теоремой Волавера о не усилении мощности при изменении соединений в электрической цепи. Согласно этой теореме, токи, которые являются откликами в электрической цепи, не превышают воздействия (по рассеиваемой ими мощности). В сетевой модели потоков продуктов отклики – валовые выпуски отраслей, должны превышать заданный спрос (план), поскольку обеспечивают также поставки другим отраслям.

Понятие поставок между людьми, частями производства, отраслями, регионами отражает суть разделения труда в процессе производства, представляя один из механизмов создания прибавочной стоимости. Поставки создают структуру производства. Сама прибавочная стоимость есть экономическое выражение физической сути биологического процесса извлечения из потока солнечной энергии дополнительной энергии, превышающей затраты на извлечение. Вообще говоря, все живое получает энергии больше, чем затрачивает на получение. Это обеспечивает возможность роста и размножения живых организмов. Передача энергии в разных формах ее накопления происходит между видами за счет того, что одни питаются другими, а в начале цепочки стоит процесс фотосинтеза зеленой массы из энергии солнечного луча.

Поставки обеспечивают создание искусственных предметов, которые становятся продуктами (товарами и услугами), и при этом не разрушаются, как при поедании в цепочке биологической иерархии, а усложняются в процессе производства конечного продукта, который идет на рынок потребления. Стоимость продуктов обеспечивает эквивалентный обмен промежуточными продуктами и конечными продуктами.

Таким образом, несмотря на внешнее сходство, потоки в сетевой модели и потоки продуктов отраслей принципиально отличаются друг от друга.

Чтобы представить поток продукта потоком в сети, воспользуемся двойственностью потоков в замкнутых и разомкнутых путях в сети. Эти потоки вызваны двойственными источниками воздействия, которые не зависят друг от друга. Отклики на них дополняют друг друга, поэтому их можно использовать для создания суммарных потоков в сети, соответствующих потокам продуктов. Для этого будем так задавать двойственные компоненты вектора воздействий (в данном случае – в замкнутых путях), чтобы отклики от них последовательно, шаг за шагом, дополняли отклики в разомкнутых путях до величин, соответствующих потокам продуктов в каждой ветви сетевой модели. То есть в ветвях, соответствующих отраслям, поставкам и ресурсам.

В терминах электротехники будем задавать источники напряжения так, чтобы отклики-токи на них дополняли отклики-токи на источники тока до таких величин, которые равны потокам продуктов. Рассмотрим условия, при которых это можно сделать полно и однозначно, где должны располагаться дополнительные источники и какие иметь значения. Решение этих вопросов позволит получить формулы, которые выражают величины потоков продуктов через величины сети, что и составит саму модель задачи баланса.

Допустим, что сначала заданы только узловые токи (представляющие спрос yα), обозначим их как Iα. Эти токи заданы на ветвях отраслей. В качестве проводимостей ветвей Yαβ примем коэффициенты прямых затрат aαβ для поставок и bγβ для ресурсов. Если отрасли не потребляют свою продукцию, то их Yαα = aαα = 1. Решая полученную сеть тензорным (или традиционным) методом, получим отклики – узловые токи в ветвях Iαc. Величинам откликов в ветвях отраслей, поставок и ресурсов добавим индексы, и обозначим, соответственно, как Iαca, Iαcq, Iαcr. Пример такой сети для трех отраслей представлен на рисунке 1. Индекс α перечисляет ветви данной сети: сначала отрасли от 1 до n, затем поставки от n + 1 до n + q, затем ресурсы от n + q + 1 до N = n + q + r, где N – полное число ветвей.

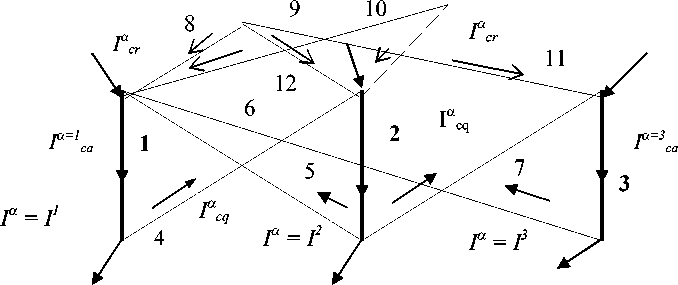
Рис. 1. Модель сети потоков продуктов с узловыми воздействиями

Стрелки на выходе отраслей (их ветви выделены жирным) показывают, что спрос задан именно в этой отрасли. Здесь ветви 1 – 3 представляют отрасли; 4 – 7 – поставки, ветви 8 – 12 представляют ресурсы. Не показаны проводимости ветвей Yαβ – коэффициенты aαβ и bγβ, чтобы не загромождать рисунок. Ориентация ветвей выбрана здесь так, что она соответствует направлениям, в которых должны двигаться потоки продуктов.

Однако реальные токи в такой сети не только не равны потокам продуктов, но и не совпадают с ними по заданным направлениям. Дело в том, что мощность уменьшается при соединении ветвей в сеть, а разность «переходит» в двойственную сеть. Поэтому отклики в ветвях отраслей не могут вырасти до величин, равных сумме заданного плана и поставок. Закон Кирхгофа для токов в узлах выхода отраслей соблюдается, но он не соответствует балансу потоков продуктов. Т.е. в данной сети с токами воздействия в разомкнутых путях баланс токов на выходе отраслей имеет вид:

I ^α = I ^α ca + Σ I ^α cq ;

• и это означает, что воздействующий ток (спрос) равен сумме валового выпуска и поставок. А в задаче баланса потоки продуктов на выходе отраслей имеют другое отношение

I ^α ca = I ^α + Σ I ^α cq

• – валовой выпуск равен сумме спроса и поставок. Таким образом, прямой аналогии между токами и продуктами нет, хотя структура их соединений одинакова. Чтобы привести токи к продуктам, используем двойственность замкнутых и разомкнутых воздействий. Для

этого предположим, что источники напряжения расположены в сети так, что отклики дополняют узловые токи до таких значений, какие должны иметь потоки продуктов.

Где и как надо расположить источники напряжения, чтобы они обеспечили выполнение этих условий? Общее число узлов J = 2n + k , где k показывает, сколько в данной системе есть разных типов ресурсов. На рисунке 1 представлены два типа ресурсов, k = 2, например, материальные и энергетические ресурсы. Чтобы с помощью воздействий получать любые значения откликов в ветвях сети, надо задать столько источников, сколько есть независимых путей данного типа. Они составят базис, в котором можно задать вектор потока с любыми необходимыми значениями откликов в ветвях сети. На рисунке 2 представлены примеры сетевых моделей из трех отраслей, которые снабжаются одним или двумя видами ресурсов соответственно.

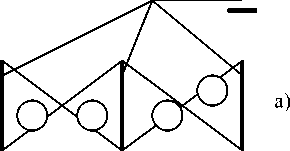
Рис. 2. Сетевые схемы моделей потоков продуктов а) – с одним типом ресурсов, б) – с двумя типами ресурсов

Всего ветвей в данной сети N = n + q + r . Если каждую отрасль снабжает ресурс одного типа, то r = n , тогда N = 2n + q . Из структуры сетей на рисунке 2а ясно, что все такие ветви выходят из одного узла (заземленного на окружающую среду).

Тогда общее число узлов в сети составит J = 2n + 1 , а число независимых разомкнутых путей равно: j = J – 1 = 2n , т.е. сумме ветвей отраслей и ресурсов. Число независимых контуров: m = N – j = q , т.е. равно числу ветвей поставок. Если в поставках расположить источники напряжения e^q α , как показано кружками на рисунке 2а, то можно подобрать их значения так, что отклики в ветвях сети будут иметь любые заданные значения. Например, допустим, что заданы источники напряжения в замкнутых путях, определяемых ветвями поставок, e^q α , такие, что отклики-токи на них в ветвях, т.е. i ^α с , примут те значения, которые нам необходимы. То есть такие значения, которые дополнят токи отклика в ветвях I ^α с (от источников тока I ^α ) до любой заданной или необходимой величины.

Если типов ресурсов больше одного, k > 1, как на рисунке 2б, то ветвей ресурсов r станет больше, чем отраслей: r > n. Тогда число узлов увеличится только на число новых типов ресурсов, т.е. первой ветви нового ресурса соответствует разомкнутый путь, а всем следующим – контуры. Для полноты определения откликов, в эти новые контуры следует поместить свои источники напряжения; это и показано кружками на рисунке 2. Итак, число узлов J = 2n + k, а независимых разомкнутых путей j = J – 1 = 2n + k – 1, т.е. не равно сумме числа ветвей отраслей и ресурсов, как для одного типа ресурса.

Процесс дополнения узловых токов контурными токами для того, чтобы представить этой комбинацией токов сети потоки продуктов, выполним за несколько итераций. Сначала допустим, что источники e α ¹ таковы, что отклики i ^α 1 , (по отраслям, поставкам, ресурсам – i ^α n1 , i ^α m1 , i ^α r1 ), вместе с откликами на I ^α составят величины, равные начальным значениям потоков продуктов при вычислении суммы степенного ряда, т.е. будут соответствовать его первому члену. Получим формулы представления потоков продуктов токами на первом этапе:

X ^α 1 = I ^α n + i ^α n1 = y ^α + x ^αβ 1 = y ^α ;

x ^αβ1 = I ^αm + i ^αm1 = 0;

• r ^γβ1 = I ^αr + i ^αr1 = y ^α .

То есть, на этом этапе отрасли производят столько, чтобы удовлетворить спрос и потребляют необходимые для этого ресурсы, не обмениваясь взаимными поставками. С точки зрения экономики, это соответствует ремесленным производствам, когда каждый производитель сам производит товар от сырья до прилавка.

Теперь допустим, что источники e α ² таковы, что отклики на них, i ^α 2 , (по отраслям, поставкам, ресурсам – i ^α n2 , i ^α m2 , i ^α r2 ), вместе с откликами на источники I ^α и откликами на источники e α ¹ , составят величины, равные значениям потоков продуктов при вычислении второго члена суммы ряда. Получим формулы для выражения потоков продуктов токами на втором этапе:

X ^α2 = I ^αn + i ^αn1 + i ^αn2 = y ^α + Σ x ^αβ2 = y ^α + Σ a αβ y ^β ;

x ^αβ2 = I ^αm + i ^αm1 + i ^αm2 = x ^αβ1 + a αβ X ^α1 = a αβ y ^β ;

• r ^γα2 = I ^αr + i ^αr1 + i ^αr2 = y ^α + Σ a αβ y ^β – Σ a βα y ^α = b γα y ^α + Σ a αβ y ^β .

При этом значения ресурсов r ^γα 2 связаны с X ^α 2 и x ^αβ 2 соотношениями, выражающими закон Кирхгофа для узлов входа отраслей. Этот закон выполняется в узлах входов отраслей при выборе источников напряжения, которые дают приращения токов в ресурсах, и с учетом соотношения, связывающего коэффициенты b γα и a αβ .

Таким образом, выбирая значения источников, можно привести комбинацию контурных и узловых токов в сети в соответствие величинам потоков продуктов в системе отраслей. То есть, сетевая модель адекватно представляет задачу межотраслевого баланса. Представить потоки продуктов только узловыми токами нельзя в силу теоремы о неусилении мощности при соединении ветвей в сети. В отраслях потоки продуктов (валовой выпуск) должны превышать спрос, поскольку необходимо еще обеспечивать поставки отраслям-смежникам. А отклики в ветвях (в том числе представляющие валовой выпуск) не могут превышать по мощности источники тока (представляющие спрос). Но нельзя представить потоки продуктов и одними контурными токами, которые не выходят из сети. Для представления продуктов в модели необходимо использовать сумму, комбинацию двойственных контурных и узловых токов.

Продолжим выбирать значения источников так, чтобы они обеспечили в ветвях на каждом этапе такую сумму узловых и контурных токов, которая равна потокам продуктов в сети отраслей при решении балансовой задачи. Тогда получим для p -ого этапа расчета следующие двойственные отклики (токи) замкнутых и разомкнутых путей, которые численно равны потокам продуктов. В совокупности они представляют компоненты, из которых состоят потоки продуктов в ветвях сети. Для валовых в ветвях отраслей выпусков отраслей получим:

ц = p      ц= p - 1

X = ia +Щ = S (a-в)"Ув = У- + a^ +(a-в)2у ■ ■1°-в)p1 у, ц=0

в ветвях поставок между отраслями:

ц = p         ц = p - 1

хав p = im +X т = S (a-в)ц у в ц =1

в ветвях ресурсов, потребляемых отраслями:

ц = p                  ц = p ^{- 1}

rpa = I- +Zi- = b- (y- +Z(a-в)ц у ) ц=1

Эти суммы независимых, двойственных контурных и узловых токов, численно равны потокам продуктов в отраслях, поставках и ресурсах, получаемым при вычислении p членов степенного ряда (при обращении экономической матрицы). Данные уравнения представляют потоки продуктов в системе отраслей (производств), как комбинацию токов (или контравариантных компонент вектора потока) в сетевой модели задачи баланса. Для расчета по частям сеть делится на подсистемы, решения которых затем алгоритмически соединяют в решение всей системы.

Спрос на выходе отраслей y ^α – внешние источники, ему соответствует вектор внешнего воздействия, который в электрической сети представлен узловым током, выход которого на выходе отраслей, а вход – на входе ветвей ресурсов.

Коэффициенты прямых затрат поставок и ресурсов a ^αβ и b ^γβ – в сети им соответствуют коэффициенты метрики, или проводимости.

Потоки валовых выпусков, поставок и ресурсов X ^α , x ^αβ , r ^γβ – отклики, которым в сети соответствуют комбинации откликов узловых токов и откликов контурных токов.

Соответствие между продуктами и сетью обеспечивают двойственные источники в замкнутых путях, для представления которых в сети вводятся источники напряжения (компоненты воздействия замкнутых путей). Структура сетевой модели такова, что эти контурные источники достаточно расположить в ветвях, которые представляют пути межотраслевых поставок. Величина контурных источников напряжения определяется итерационным процессом перехода от несвязанных отраслей к связанным отраслям, которые обмениваются своими продуктами в процессе производства. Именно включение двойственных величин в сети обеспечивает представление процессов в живой, в данном случае – экономической системе с помощью комбинации двойственных величин в сети – неживой электрической цепи. Двойственные отклики замкнутых и разомкнутых путей в совокупности представляют сумму компонент – потоков продуктов:

Эти суммы независимых, двойственных контурных и узловых токов, численно равны потокам продуктов в отраслях, поставках и ресурсах.

Структурно-двойственный механизм моделирования живой системы

Таким образом, структурно-двойственный механизм моделирования живого следующий. Внешнее воздействие на живую систему приводит к отклику внутри системы.

Система внутри создает воздействия, которые уменьшают внешнее влияние, а часть проходящей энергии переключают на свой рост. Внутренние воздействия создают потоки, которые увеличивают притоки энергии от внешнего воздействия.

Энергетическая задача организма состоит в увеличении той части внешнего потока энергии, которую организм может использовать на поддержание своей деятельности.

Из внешнего потока энергии часть проходит мимо организма, часть проходит через организм и либо требует затрат для защиты организма, либо не требует, а часть организм может использовать для сохранения своего состояния или размножения и развития.

Механизм моделирования или физического создания механизма с такими функциями можно создать с использованием свойств сетевой структуры.

Особенности этих свойств выражает инвариант двойственности даже для одномерных сетей. Для многомерных сетей должны существовать свои аналогичные инварианты.

Расширение свойств и возможностей структуры для моделирования и создания искусственных живых организмов пойдет по линии полиэдральных сетей и с привлечением колебаний, волн и частотных характеристик.

Аналогии экономической системы и живого организма. Система дыхания и доставки окислителя к месту преобразования энергии, питания и доставки энергии, смазки, управления и контроля, получения сигналов о состоянии внешнего мира и внутреннего состояния организма.

Примером применения свойств двойственности сетей является сетевая модель баланса потоков продуктов в системе производства. Это сетевая модель известной задачи межотраслевого баланса (МОБ). В сетевой модели МОБ – спрос представляет узловой ток, но отклики не равны, не соответствуют продуктам. Надо удвоить узловой ток, ввести ЭДС, которые приведут продукты к производству спроса. Это соответствует первому члену степенного ряда при вычислении обратной матрицы к экономической матрице (или матрице Леонтьева). Затем надо увеличивать ЭДС, (в соответствии с топологией сетевой модели они должны располагаться в поставках) – если в модели один тип ресурса – до тех пор, пока не будет достигнуто соответствие продуктов и комбинации контурных и узловых токов. Т.е. токов отклика на внешние и внутренние воздействия.

Этому воздействию соответствуют напряжения узлового и контурного типа, которые в экономике представлены деньгами, а в биологии мотивациями или стимулированиями действий, приводящих к увеличению свободной энергии. Спросу в экономике соответствуют потребности в поддержании конструкции, движения и тепла в живом организме.

Представление структурно-двойственного механизма в LT-таблице

Каждой предметной области в LT-таблице соответствует «пятерка» клеток-величин. Две из них определяют воздействия и отклики, которые меняются местами в замкнутых и открытых системах. Две другие представляют отношения между воздействиями и откликами; продольными и поперечными величинами, которые являются обратными для замкнутых и открытых систем. Пятая величина – мощность, произведение продольных и поперечных величин, которая характеризует потоки энергии через систему в данной предметной области. Можно классифицировать все предметные области по «структуре» их представления в таблице LT. Более того, для многомерных процессов возникают свои конфигурации величин, которые взаимодействуют между собой, а также с одномерными процессами. Их также надо включить в классификацию. Такая таблица с конфигурацией отношений между величинами воздействий – сопротивлений – откликов в замкнутых и открытых системах для одномерных и многомерных процессов может применяться не только для классификации известных систем, но и для предсказания, прогнозирования новых видов систем, которые еще неизвестны в настоящее время∗.