Класcы преобразований нестационарного сигнала в информационно-измерительных системах. I. Элементы теории

Современные методы обработки сигналов, такие как кратковременное преобразование Фурье, преобразования Зака и Габора, билинейные преобразования класса Коэна (преобразования Вигнера, Бесселя, Бертрана, Вилсона и их модификации), преобразования время—масштаб (разновидности вейвлет-преобразований и вейвлет-пакеты, обладающие хорошей локализации свойств сигналов), не нашли пока широкого применения. Поэтому актуальной является задача разработки методического и алгоритмического обеспечения обработки локально-стационарных сигналов в информационных и информационно-измерительных системах (ИИС), в частности для контроля процессов со спорадическим характером изменения статистических свойств [1] и для фильтрации, основанной на контроле характеристик шума в течение кратковременных пауз полезной составляющей сигнала [2].

Перечисленные виды преобразований обеспечивают двумерное представление, которое в явной форме отражает динамику частотной структуры сигнала. Это может позволить решать задачи локализации свойств сигнала, например квазиста-ционарных сегментов сигнала при контроле потока нефти с интервалами включения газовой фракции или пауз информационной компоненты речевого сигнала, для оценки характеристик шума с целью адаптивной формы его фильтрации.

Отдельным преобразованиям (Вигнера, Зака, вейвлет) посвящены обширные исследования [410], по другим имеются только сведения о структуре. Вместе с тем не существует однозначного преимущества и предпочтительности единого преоб-разования.[11-12]. Поэтому для корректного применения преобразований нестационарных сигналов в ИИС предлагается краткая сводка элементов теории, а также взаимосвязи и свойств классов время-частотных и вейвлет-преобразований.

Оба класса преобразований дают представление сигнала $ ( t ) е L ² в форме интеграла или дискретного разложения в виде суммы ряда по базисам соответствующих классов: один образован модулированием единой образующей функции (когерентными состояниями Вейля—Гейзенберга), другой образован сдвигом и растяжением (аффинным преобразованием времени) образующей функции, которая определяет тип преобразования. Анализ обнаруживает тесную взаимосвязь двух классов преобразований и помогает использовать различные формы их характеристик, которые наиболее соответствуют особенностям сигнала и требованиям задачи его обработки в ИИС. Среди таких требований может быть наличие быстрого алгоритма реализации, существенность фазовой информации или приоритет локализации энергетической характеристики сигнала.

КЛАССЫ ПРЕОБРАЗОВАНИЙ И ИХ ВЗАИМОСВЯЗЬ

Время-частотное преобразование (ВЧП) Габора [4, 13], его расширенная форма — кратковременное преобразование Фурье (КВПФ) F $ ( t , to ) и время-масштабное (вейвлет) преобразование T_s ( t , a ) сигнала $ ( t ) представляются в виде (1)-(3) при условном обозначении (• , •) — для скалярного произведения и ф_ю ( т ) = ф ( т - 1 ) exp( - j toT ) — для квазибазисного элемента разложения (где ф — временное окно):

G ( t , ^to ) =

∞

= / $ ( т ) g( т - 1 )exp[ - j to ( T - 1 /2)]d r ;     (1)

-∞

^

F s ( t , to ) = J s( т ) ф *( t - t ) e ^{- j toT} d T ,

-^

F_s ( t , to ) = ( s , ф , _т Y       to e R ;

E_s = J s ²( t ) dt = JJ| F s ( t , to )|² d t d to =

Я ।    , _x ,2 d t d a

| T s ( t , a Г ..                             (8)

a ²

T s ( t , a ) =

^

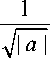
J s ( t ) ¥

-^

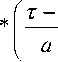
t )

d r ,

T s ⁽ t , a ) = ( s , ¥ t , a Y

¥ t , a ^{( t} ) =

T

t

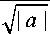
a

При этом для КВПФ и вейвлет-преобразования (ВП) необходимы условия:

С ф = J1 Ф^ ) |² d v < ~ — Фурье, C _¥ = J | ¥ ( v ) 1 ² 1 v | ^{- 1} d v < ~ — вейвлет.

Использование спектрограммы и скейлограммы занимает значительное место в представлении энергетического состава речевых сигналов людям с повреждением слуха. Однако это только одна из форм совместного время-частотного и время-масштабного анализов.

Обширный подкласс время-частотных преобразований составляют билинейные ВЧП, представителем которых является преобразование Вигнера—Вилле [3, 12, 15]

W_s ( t , to ) = J s ( t + т /2) • s *( t - т /2) • e ^{- j toT} d T . (9)

Таким образом, КВПФ и ВП — это различные, но в определенном смысле эквивалентные линейные преобразования, и возможно перейти от одного к другому без потери информации. Для нормировки С _Ф = С _¥ = 1 взаимосвязь этих преобразований выражается соотношениями:

T s V ) = JJ F TT    ^ " V a T )   ^{d T d} " , ⁽⁵⁾

вейвлет КВПФ вейвлет - преобр.

окна КВПФ

F s ⁽ t , ^{to a} ) = JJ T s ( T ^a )     < ¥ тта . Ф tto ) ^{d T d a} / ^{a 2}. ⁽⁶⁾

^ ^ ¹       ^ V ¹    <  ^{v 1}

КВПФ вейвлет КВПФ от ¥_{T a}

Взаимосвязь преобразований явно отражается случаем, когда не нужна фазовая информация и важны только энергетические характеристики сигнала. При этом используется спектрограмма — квадрат модуля КВПФ | F s ( t , to ) |² и скейлограмма — квадрат модуля вейвлет-преобразования | T s ( t , a )|². Равноценность полученных оценок величины энергии сигнала связана с применением нормировки С _Ф = С _¥ = 1, при которой оба преобразования могут быть обращены и восстановлено (7) одно и то же значение сигнала s ( t ), и с изоморфизмом преобразований (т.е. с равенством нормы сигнала и его преобразования в L ²) — согласно соотношению (8):

^{s (} t ) = JJ F s ^{( т} , " ) • Ф т" ⁽ t ^{)d T d} " s ⁽ t ) = JJ T s ⁽ T ^a ) • ¥ Ta ⁽ t ) d ^T" .       ()

Преобразование имеет ряд свойств. Это — вещественность, корректность маргиналов, согласно соотношениям (10), (11), инвариантность к сдвигам по времени (согласно выражению (12)) и по частоте (13), а также выполнение соотношения Мойела (14), которое отражает унитарность преобразования Вигнера [16]:

J Ws (t, to)d t =|s(to )|2,

J Ws (t, to )dto =|s (t )|2,(11)

st ,to(T) =s (T - t) •e - jtoT^

^ Wst,to (T,") = Ws (T -1," - to),(12)

s a ( ^T ) = | a I     • s ( a ^T ) ^

".

^ W s „^{( T} , " ) = W s ^{( a T ,}-⁾ ,      (13)

a a

« W s , W s 1» = JJ W s ( t , " ) • W s 1 ( t , "  )d T d " =

= K s , s ! ) |².                                              ⁽¹⁴⁾

Свойство корректности маргиналов дает основание называть преобразование Вигнера распределением, т. к. интегрирование его по времени дает мощность сигнала по частоте (10), а интегрирование по частоте дает мощность по времени (11).

Из определения спектрограммы, свойства инвариантности к временному сдвигу (12) и из соотношения Мойела (14) следует, что спектрограмма кратковременного преобразования Фурье имеет три эквивалентные формы выражения:

| Fs (t,to)|2 =|

по (14)

=« ^W s , ^W» _t , to » =

= JJ W s ( t , " ) • W ф ( T - 1 , " - to )d T d " .

Аналогичным образом из определения скейло-граммы, из свойств корректности маргиналов (10), (11) и из ковариантности к изменению масштаба (13) могут быть получены три формы выражения скейлограммы:

I T s ( 1 , а )|² =К s , w _t , а я² =

= « W s , W _Vt , a » = (16)

= JJ Ws (t,£). wv(—, al)dT d^.

V a J

Соотношения (15) и (16) отражают взаимосвязь кратковременного преобразования Фурье (основу построения спектрограммы) и вейвлет-преобразования (основу скейлограммы) с преобразованием Вигнера—Вилле. Спектрограмма получается через распределение Вигнера—Вилле путем корреляции последнего, а скейлограмма получается с помощью так называемой аффинной корреляции двух распределений Вигнера (с масштабированием аргументов одного из них). Аффинная корреляция — это корреляция с частичной зависимостью, т.к. при ее получении масштабируется частота.

Для хорошо локализованных базовых функций вейвлет-преобразования соответствующее распределение Вигнера можно интерпретировать как низкочастотные функции (размерности два), действующие как локальные сглаживающие фильтры. Это и объясняет более высокую разрешающую способность ВЧП Вигнера сравнительно со спектрограммой и скейлограммой.

К недостаткам преобразования Вигнера следует отнести появление кросс-членов, связанных с интерференцией отдельных частот сложного сигнала, а также возможность появления отрицательных значений, которые трудно интерпретировать. Первый недостаток успешно преодолевается существующими модификациями распределения Вигнера—Вилле (преобразования псевдо-Вигнера и сглаженное псевдо-Вигнера) [3, 14, 16].

s(t)           ^

Д si = s(1 - T )e "j™ ‘    ^

Использование этой схемы показывает, что любое ядро (с четырьмя параметрами) должно удовлетворять свойству (19)

K ( т , т '; 1 , т ) = K ( т - 1 , T- 1 ; 0,0)exp[ - J ® ( t -т ')] (19) и, следовательно, должно зависеть только от двух

ПОСТРОЕНИЕ ПРЕОБРАЗОВАНИЙ

Возможна другая форма представления распределения энергии сигнала. Показано, что спектрограмма и скейлограмма — результат некоторой корреляции (в случае вейвлет-преобразования это аффинная корреляция) между двумя распределениями Вигнера—Вилле (от сигнала и от базисной функции). Это может быть обобщено и на другие распределения (результаты преобразований) при условии, что они инвариантны к сдвигу по времени, ковариантны к изменению масштаба и унитарны, т.е. удовлетворяют соотношениям (12)-(14). При таких условиях могут быть созданы группы распределений энергии [12], а спектрограмма и скейлограмма будут только частным случаем. Метод такого подхода заключается в следующем [14, 15].

• 1.    Спектрограмма, скейлограмма и распределение Вигнера — это нелинейные преобразования, и при использовании ядра общего вида K ( т , т ', 1 , т ) все они могут быть представлены в единой форме соотношением

• 2.    На распределение накладываются требования ковариантности к сдвигу по времени и по частоте. Исходя из этих требований определяются необходимые свойства допустимого ядра.

• 3.    Добавочные требования на распределение (преобразование) в некоторых случаях приводят к единственному решению для ядра.

R s ( t , Я ) =

= JJ K ( т , Т , 1 , Я ) • s ( т ) s * ( т ') d T d T '. (17)

Такой способ определения общей формы ядра приводит в качестве частных случаев к известным преобразованиям. Для время-частотного преобразования требования ковариантности по времени реализуются по схеме, представленной выражениями (18):

R s ( 1 , ™ )

Д

R. , ^{( 1} , ^т ) = R s ^{( 1 - т} , ^{т -} ™ 1 ^). тт

независимых переменных. Это можно сравнить с инвариантностью к сдвигу времени, которая превращает линейный оператор в фильтр.

Так получается обширный класс допустимых время-частотных преобразований, которые определяются произвольной функцией от двух переменных [12, 14, 15]. Это класс Коэна. Самая простая форма преобразования этого класса имеет вид

C s ( t , ю , П ) = JJ W s ( т , £ ) П( т - t , £ - ю )d т d ^ . (20)

Соотношение (20) подчеркивает значимость распределения Вигнера, т. к. любое преобразование класса Коэна может быть представлено как корреляция преобразования Вигнера W s с произвольным ядром П. Другое представление распределения (т. е. результата время-частотного преобразования Коэна) для любого сигнала s ( t ) может быть получено из выражения (21)

C s ( t , ю , П ) = JJ A s ( ^ , т ) f ( ^ , т ) e '" ⁾d т d 2 , (21) в котором A_s($ , т) — двумерное преобразование Фурье от распределения Вигнера

Ws (t, ю) ^ As (^,т) = Ws (т, 5), f$, т) — двумерное преобразование Фурье от ядра П, которым определено преобразование Коэна:

/X

П ( t , ю ) ^ f ( £ , т ) = П ( т , ^ ).

После того как класс преобразований определен, на него можно наложить дополнительные требования и найти соответствующие им условия, которые должны выполняться для ядра П ( t, го ) или для его Фурье-преобразованной частотной формы f$ , т ). При этом представляется возможным накладывать либо все, либо часть из перечисленных ниже условий, которые могут задавать набор желательных свойств преобразования. Каким условиям должна удовлетворять частотная форма ядра f$ , т ) для реализации различных свойств преобразования, показывают соотношения (22)-(29).

• 1.    Вещественность преобразования Коэна:

• 2.    Согласованность преобразования (в качестве время-частотного распределения) с энергией сигнала E_s :

• 3.    Корректность маргиналов, т. е. верное представление энергии сигнала в частотной и временной областях (при проинтегрированной второй переменной распределения):

• 4.    Ковариантность к изменению масштаба:

• 5.    Выполнение соотношения Мойела (унитарность):

Cs (t, ю; П )е R   ^ f (^,т) = f (-^,-т).  (22)

( тогда и только тогда)

JJ C_s ( t , ю ; П )d t d ю = E_s   ^ f (0,0) = 1.   (23)

C s ( t , ю ; П )d t =1 s » | ² ^ f (0, т ) = 1, г                         ,                      (2 ⁴ )

J C s ( t , ю ; П )d ю = | s ( t )|² ^ f О) = 1.

Csa (t,ю;П) = Cs(at,ю;П) ^ f (£т) = f3(^т), (25) aa где f0 — функция одного параметра.

« C s ( П ), С ^( П )» =К s , s 1 > |² ^ | f ( ^ , т ) = 1. (26)

Преобразования Коэна являются обобщением широкого класса время-частотных преобразований. Но преобразования Коэна могут таким же образом характеризовать и класс время-масштабных преобразований. Изменяя обозначение X ^ а в соотношении (17) и в полученных из него выражениях и заменяя сдвиг по частоте операцией изменения масштаба, можно получить требование ковариантности к сдвигу времени и масштаба в форме, представленной соотношением (27):

s ( t )             ^

U

5ат =| а |-1/2 s| t—т | ^ I а )

R s ( t , а )

U

Rs  (t, а) = Rs I t sат v     7 s

- т

а

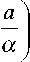
Так же как и во время-частотном классе, после определенных преобразований можно получить для ядра условие, выполнение которого гарантирует желательные свойства время-масштабного преобразования. Требование ковариантности преобразования к изменению параметра масштаба по соотношениям (27) можно привести к условию (28), необходимому в этом случае для ядра. Условие получается после преобразований, аналогич-

ных выполненным выше при рассмотрении время-частотного распределения Вигнера:

K( т , т' , t , а ) = | а | ^{- 1}

• K f —, — ,0, 1 ' | a a J

Условие (28) снова снижает до двух число переменных и определяет класс время-масштабных преобразований Q в виде (29):

= JJ W s ( T , ^ ) . П

Q s ( t , a ; П) =

,a^ | dTd^ = a J

= f J A s ( § , t ) • f ^f a ^ , ^T \ • e -^{j( 5 t} > d r d ^ .      (29)

I a J

При этом время-масштабное преобразование оказывается выраженным либо через преобразование Вигнера (путем взвешивания его ядром П), либо через преобразования Фурье: (двумерные) A s и f от преобразования Вигнера ( W) и от ядра ( П) соответственно.

В этом классе также можно ввести дополнительные требования на свойства преобразования и привести их в дополнительные условия, которым должно удовлетворять ядро. Требование вещественности преобразования соответствует условию сопряженной четности двумерного преобразования Фурье f£т ) ядра П :

Q s ( t , a , П ) е R ^ f ( 5 , т ) = f *( Ч, -т ).    (30)

Согласованность преобразования с полной величиной энергии сигнала соответствует (аналогично (23)) условию (31) для ядра П ( t , a ) этого преобразования:

„ d t d a   „             . d t d a ,

Qs(t,a,П)—r = Es ^ П(t,a)^V = 1 (31) a2                                     | a | где Es = Js(t)2dt = J| s(m) |2 dm.

Требование правильности соответствия маргиналов преобразования и мощности сигнала при ее выражении во временной и в частотной областях приводит к условиям (32) и (33):

J q s ( t , a ; П )d t =

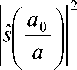
^ f (0, t ) = e ~^{2 n ja 0} ' , (32)

f Q s ( t , a ; П )d a = | s ( t ) |² ^

J             a

J f ^f a ^ , ^T \ da = S ( t ). (33)

^J | a J a

Требование унитарности, которое фактически выражается формулой Мойела и в рассматриваемом случае имеет вид (34), приводит к условию (35), выражающему ортогональность двумерных преобразований Фурье f от ядра П :

JJ Q s ( t , a ; П ) • Q * 1 ( t , a ; П)^ = 1 ( s , s 1 ) ^     (34)

$ f T A *f   TA d^ da f\a^-\-f \a^-\—— = S (т - t').   (35)

| a J| a J a

Класс преобразований Коэна относится в основном к время-частотным преобразованиям и да- ет соответствующее распределение нестационарного измерительного сигнала в плоскости время— частота. Как видно из соотношений (25), (27)-(29), класс построенный по тому же принципу, но с использованием аффинной ковариантности приводит к время-масштабным преобразованиям. Эти два класса имеют внутреннюю взаимосвязь. Можно, например, считать, что преобразование Вигнера принадлежит обоим классам. Кроме того, в некоторых случаях распределению энергии при преобразовании класса время—масштаб может быть дана время-частотная интерпретация в форме, аналогичной маргинальному свойству по соотношению (23).

С некоторой степенью условности возможно формально идентифицировать масштаб и обратную частоту по выражению m = m ₀ / a , где m₀ — некоторая частота. При такой интерпретации оказывается, что все время-масштабные распределения (преобразования с корректными маргиналами) характеризуются функцией такого ядра, которое в частотной области представляется в виде (36):

f ( ^ , т ) = f 0 ( ^7 ) • e j ^{0 т} , (36)

где f 0 — функция одного аргумента: произведения ^т [12, 16]. Эта функция такова, что служит для создания ядра П время-масштабного преобразования. Это ядро выражается через ядро типа Коэна П 0 , но для получения весовой функции П 0 , образующей это ядро, используется ее время-частотное представление f 0 . Это утверждение выражается соотношением

Qs (t, a; П) = Cs (t, m0; П3), (37) a где П0 — время-частотное представление функции f >, т. е. П0 = БПФ-1(БПФ-1 f 0).

Эта взаимосвязь преобразований (или распределений энергии сигнала в двух формах) объясняется тем, что распределения имеют общность, связанную с требованиями ковариантности к сдвигу частоты (ВЧП) и ковариантности к изменению масштаба (ВП). Такая интерпретация может быть дана не всем время-частотным распределениям. Так, скейлограмма не ковариантна к сдвигу частоты.

Считается, что ограниченность частотной полосы вейвлет-преобразования достаточна для интерпретации его в терминах фильтрации. Однако это справедливо для одномодального спектра вейвлет-базиса, но не выполняется при многомодальном спектре у вейвлет-функции.

В работах по анализу взаимосвязи двух классов преобразований проводилась известная аналогия переменной масштаба с аккордами, поэтому ее соотношение с частотой лучше для понимания в форме обратного отношения ю1/ ю2 = a 2/ a 1. Это соотношение подчеркивает также характер преобразования частот в операциях, связанных с изменением масштаба. Делая функцию ядра зависящей от некоторой частоты ю0, можно получить распределение, основанное на частотной переменной ю0 /а. Эта частотная переменная может быть формально идентифицирована с обычной частотой в преобразовании Фурье с той разницей, что она не может быть отделима от частотного разрешения Аю, так что относительная ширина полосы Аю/ю постоянна (постоянное качество анализа во всем частотном диапазоне, характерное для вейвлет-преобразования). С формальной точки зрения результирующие распределения могут быть использованы как определения время-частотных распределений независимо от способа их получения.

НЕСГЛАЖЕННЫЕ ПРЕОБРАЗОВАНИЯ (РАСПРЕДЕЛЕНИЯ)

Как показано выше, время-масштабные распределения (аффинный класс) получаются из распределения Вигнера—Вилле действием оператора корреляции. Часто эта корреляция принимает форму сглаживания, как в случае скейлограммы. Но это бывает не всегда. В классе время-масштабных преобразований можно рассматривать подкласс такой, что ядро, определяющее его, имеет форму f (5,т) = G(5) • e(5)т ,              (38)

где Н ( 5 ) и G ( 5 ) — произвольные функции.

Это очень существенно отличается от аффинного сглаживания распределения Вигнера тем, что этот вид двумерного преобразования от ядра не соответствует низкочастотной функции пропускания — фильтру. Вместе с тем эта форма определения ядра в частотной области дает широкий набор преобразований. Для полученных преобразований имеется возможность формировать их полезные свойства, накладывая требования на ядро в частотной форме (38). Согласно данному определению ядра, соответствующее преобразование имеет вид

Q , ( t , a ; П ) =

= [ g ( a 5 )/ HOI - 5 1 / Г H 5 ₊ 5 L

• ¹    I a 2 II a 2 ,

x exp( - 2 П j 5 t )d 5 .                          (39)

Таким образом, формирование новых преобразований с хорошими свойствами получается на основе приведения желаемых свойств к форме требований к ядру и выражения их в виде требо- ваний к функциям Н(5) и G(5), определяющим частотную форму ядра.

СОЗДАНИЕ РАЗЛИЧНЫХ ПРЕОБРАЗОВАНИЙ

Создание преобразований при использовании рассмотренной последовательности действий сводится к решению уравнений, составленных для функций Н ( 5 ) и G ( 5 ), которые входят в частотное представление ядра формируемого преобразования. Выполнение процедур, связанных с созданием преобразований на основе описанного принципа, можно проследить на процедуре получения двух время-масштабных преобразований: преобразования Бертрана и преобразования, введенного Фландрином [16, 18].

Такой же метод применим для получения вре-мя-частотных преобразований.

• 1.    Преобразование Бертрана [17] может быть получено на основе требования унитарности, т. е. выполнения соотношения Мойела, и требования высокой локализации преобразования по времени (высокой его разрешающей способности). Использование выражения (26) и частотной формы ядра в виде (38) приводит к дифференциальному уравнению (40), определяющему связь функций Н ( 5 ) и G ( 5 ):

G ²( 5 ) = н ( 5 ) - 5 • H!¹ .          (40)

d5

Ограничение на временнýю локализацию, состоящее в выполнении (41), ведет к условию (42):

S>( v ) = | V Г¹/ ² exp( - 2 n j v 1 0 ) ^

^Q , ( t , a ; П ) = | a | - 5 ( t - 1 o ),

G 2 ( 5 ) = н ²( 5 )

-

Отметим, что (42) приводит к дополнительному требованию Н ( ξ ) > |ξ| / 2. Сравнение выражений (40) и (42) для G ² ( ξ ) приводит к дифференциальному уравнению для Н ( ξ ), решение которого определяет функцию Н ( ξ ) в виде (43)

н (5) = Г 5 )■ cthf5

V 2 7 V 2

После этого G ( ξ ) может быть выражено соотношением (44)

G ( 5 )

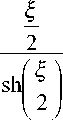
Подстановка этих выражений в ядро, форма которого приведена в (39), и использование получившейся аналитической формы ядра для создания преобразования приводит к окончательному выражению для преобразования Бертрана [9, 16, 18]. Преобразование Бертрана (или распределение Бертрана в плоскости время—масштаб) определяется соотношением (45):

выражения ядра (в частотной форме) позволяет с помощью соотношения (39) получить окончательное выражение преобразования Фландрина [8, 16, 18]:

D s ⁽ t , ^a ) =

B_s ( t , a )

=--X

| a |

-J

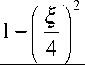
| a |

a

V

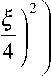
a

V

⁽ 1

А* • 5

1+51

4 J

7 J

x

5 xj .25

7?   7 £77

— exp||

2      V 2 J

2 J

V

, ( 5 a • sh —

I 2

• 5

7?   7^77

— • exp| — |

2 h J

(       (t

x exp - 2nj5\ -

V

, ( 5 a • sh —

I 2

X

V

a

d 5 .

ОБЩИЕ ЗАКЛЮЧИТЕЛЬНЫЕ ПОЛОЖЕНИЯ

x exp - 2nj5 •

V

2. Преобразование Фландрина описано, в частности, в [9, 16, 18]. Создание время-масштаб-ного преобразования Фландрина (и соответствующего распределения для сигнала) основано на требовании наличия корректного временнóго маргинала. В то же время не используется ограничивающее требование унитарности, формализованное соотношением Мойела. Согласованность интеграла преобразования по параметру масштаба с энергией сигнала

JQ , ( t , a ; П )^ - | s ( t ) |²

a ²

накладывает условие (47) на ядро (более точно, на его частотную форму, которая является двумерным преобразованием Фурье от ядра):

Jf( a5,T 1 da = 5 (t).           (47)

J V a J a

Можно показать, что это ведет к условию

G ( 5 ) = H ( 5 ) - 5 dH^ ⁵ )- .             (48)

d5

Дополнительным требованием к преобразованию является временнáя локализация, которая, как и в случае преобразования Бертрана, приводит к соотношению (42). Совместно выражения (42) и (48) позволяют решить уравнение для Н ( 5 ) и затем найти G ( 5 ) .

н ( 5 ) = 1 +

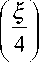
^ G( 5 ) = 1

-

Выражения для Н ( 5 ) и G ( 5 ) полностью определяют ядро преобразования. Знание аналитического

Проведенный анализ показывает основную методическую схему создания различных преобразований нестационарного сигнала в ИИС на основе обобщенной формы представления классов преобразований и введения некоторых требований к математическим свойствам преобразования. Это — требования унитарности (выражающейся соотношением Мойела), временнóй локализации, выполнения у маргиналов соотношений, отражающих правильное выражение энергии сигнала в частотной и временнóй областях. Преобразования с корректными маргиналами наиболее обосновано называют распределениями, хотя в области обработки сигналов распределениями называют и другие преобразования, имея в виду представление результата преобразования сигнала в координатах время—частота или время—масштаб.

Некоторые замечания могут быть сделаны о свойстве локализации распределения энергии сигнала в результате преобразований рассмотренного класса. В отношении локализации по частоте и предела ширины полосы разрешения имеет значение различие между двумя концепциями — частоты и масштаба, которые связаны с двумя общими классами преобразований и которые естественным образом входят в способ интерпретации понятий локализации и разрешения. Если рассматривать преобразования время-частотного класса (аффинные), то общая форма их выражения может быть представлена различным образом:

— как свертка аффинно-преобразованного ядра с преобразованием Вигнера от сигнала;

— как обратное преобразование Фурье (БПФ-1) от скалярного произведения частотной формы преобразования Вигнера с аффинным преобразованием частотной формы ядра;

— как преобразование Вигнера от частотной формы сигнала с включением весовой функции.

Первые две формы представления преобразования даны выражением (51), а третья форма представления — выражением (52):

Q s ( t , a ; П ) =

= jj W s ( - 6 ) •

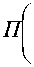
^T —-, a • 6 | d t d 6 = a J

= fU(6,t) • f | a • 6,- Ie2d6 dt, I a I

Q s ( t , a ; П ) =

jj V (a 6 , v ) •

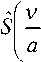
6 I ² 1

• S

f-+-1

I a 2 I

X

Оказывается, что при принятом выше условии обычное преобразование Вигнера—Вилле может рассматриваться как узкополосный предел некоторого время-масштабного преобразования (и распределения как результата этого преобразования). В этом смысле время-масштабные преобразования можно интерпретировать как время-частотные путем формальной идентификации ν = ν 0 /a . Вследствие этого о них можно говорить как о широкополосных разложениях преобразования Вигнера—Вилле или как о время-частотных преобразованиях, приспособленных к широкополосным сигналам.

В случае локализованных ядер, зависящих от двух частот, типа f (6,-) = G(6) • exp[-2пр H(6)-],        (56)

x exp( - 2 n j - 1 )d - d t .                (52)

условие (57)

Здесь ψ ( ξ , ν ) заменяет произвольную функцию ядра, зависящую от двух частот.

В случае сигнала, состоящего из одной спектральной линии S( v ) = 5 (v - v 1 ), выражение (52) сводится к a∙ψ ( 0, aν 1 ). Это означает, что если для функции выполняется условие ψ( 0 , ν) = δ ( ν – ν 0 ), то само распределение точно локализовано по частоте согласно выражению (53):

Q , ( t , a ; П ) = 8 ^f - v , ) , v , =    ,    a = ^ . (53)

I a I a v1

Справедливо более общее положение. Если анализируемый сигнал узкополосный и спектр его занимает малую окрестность около некоторой центральной для него частоты, то эффективное интегрирование по ξ ограничено малой областью вокруг начала. В этом случае влияние функции ядра главным образом зависит от локальных свойств его разложения Тэйлора:

W (a - , v ) = ^ (0, v ) + a - ^ (0, v ).         (54)

d-

^(0,v) = 8(v -vo), |^ (0,v) = 0 d6

может быть представлено в виде (58):

H (0) = v 0 , G (0) = 1, Ц (0) = | G (0) = 0. d 6 d 6

В такой форме эти условия выполняются при создании уже упоминавшегося преобразования Бертрана (45). Использованные при его получении соотношения у (0, v) = 5(v - v₀) и ^ ^ (0, v ) = 0 при d 6

интерпретации время-масштабного преобразования в терминах времени и частоты могут служить для выбора ν 0 в качестве единицы измерения частоты. При этом само значение ν 0 можно брать произвольно в соответствии с общим представлением о частотном диапазоне контролируемого в ИИС нестационарного сигнала.

Тогда, если можно принять, что ψ (0, ν ) = δ ( ν – ν 0 )

и

f d^ )

(0, v ) = 0 , то получится аппроксимация

d6 II преобразования в форме выражения

Q s ( t , a ; n ) ^

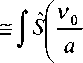
^{- 1} Z S * ^f ^ - + ^{- 1} exp( - 2 n j - t )d - =

² ) ( ^{a 2} )

= W_s ^f t , ^V 0- .

^{1 a} )