Класcы преобразований нестационарного сигнала в информационно-измерительных системах. IV. Соответствие формы ковариантности и вида время-частотного преобразования

ВВЕДЕНИЕ                      пользовано расширение понятия "ковариантность".

Ковариантность — это свойство, отражающее вид

Основой совершенствования методов анализа нестационарных сигналов в информационно-измерительных системах (ИИС) служат формы их обработки на основе время-частотных и время-масштабных (вейвлет-) преобразований. Для этих двух классов преобразований созданы концепции их построения, систематизированы свойства вре-мя-частотных преобразований (ВЧП) (связанные с характером и точностью представления сигнала), определена мера общности двух классов преобразований и показаны их преимущества над классическими формами спектрального анализа [1–5].

Наиболее практически значимыми являются билинейные ВЧП (часто называемые также квадратичными). Построение ВЧП этого класса (называемого классом Коэна (L. Cohen) [6, 7]) основано на использовании интегрального преобразования билинейной функции сигнала, взвешенной ядром. Вид и свойства ядра определяют тип ВЧП и его особенности. Однако в последнее время появилась новая методология построения квадратичных ВЧП 1), которая позволяет значительно увеличить степень их разнообразия.

При преобразованиях, связанных с получением аналитических выражений новых типов ВЧП, их характеристик, свойств и особенностей, будет ис- модификации ВЧП при некоторых преобразованиях анализируемого сигнала. В качестве таких преобразований обычно рассматриваются те или иные формы изменения масштаба сигнала и его временнóго сдвига (или преобразования частотного спектра сигнала в области его преобразования Фурье). Однако при анализе ВЧП понятие ковариантности ассоциируется главным образом с характером различных типов преобразований параметров времени и частоты для аргументов результата преобразования. В этом случае вид соответствующего преобразования сигнала рассматривается на втором плане как причина, порождающая анализируемое свойство ковариантности ВЧП 2).

Конкретная форма свойства ковариантности определяет специальную группу ВЧП, которые имеют особенности аналитического выражения, вид ядра и приспособленность ВЧП к анализу сигналов с определенным характером распределения энергии в плоскости время—частота.

Для краткости каждой форме свойства ковариантности и группе ВЧП, которой этот тип ковариантности свойственен, будет дано промежуточное название. Например, группа ВЧП, которая получается на основе формирования свойства ковариантности к одновременному масштабированию вре- мени и частоты

H_{c; s} ( t ; f ) = H ( at ; f I a )

пРи CaS(f) = (1I'j\»\ ) s(f 1 aX а также удовлетворяет свойству ковариантности к "гиперболически" частотно-зависимому сдвигу по времени

Hh_cS ( t ; f ) = H ( t - c / f ; f )

при ⁽ H c s ^{)( f} ) = exp ( 2 ⁿ jc ln ^{( f 1} f_r ) ) • s ^{( f} ), условно называется группой гиперболических время-частотных преобразований (Г-ВЧП)³⁾.

Анализируемая модификация Г-ВЧП связана с сигналами, у которых распределение энергии в плоскости время—частота по форме близко к гиперболической зависимости (~ ll f ). В этом случае Г-ВЧП обеспечивает существенно лучшее разрешение сравнительно с любым ВЧП класса Коэна.

ГРУППА ВРЕМЯ-ЧАСТОТНЫХ ПРЕОБРАЗОВАНИЙ С КОМБИНИРОВАННЫМ СВОЙСТВОМ КОВАРИАНТНОСТИ

" Гиперболическая" группа (или класс) ВЧП, условно называемых Г-ВЧП, порождается при введении свойства ковариантности в комбинированной форме.

• ■    Ковариантность ВЧП П s ( t ; f ) в форме одновременного масштабирования времени и частоты П_с - ( t ; f ) = n s ( at ; f I a ) при условии масштабирования частотного спектра сигнала s ( t ) (в области его преобразования Фурье s ( f )):

C_aS ( f ) = —s ( f I a ), где t и f — время и частота.

I ^a I

• ■    Ковариантность ВЧП П_s ( t ; f ) в форме "гиперболического" сдвига времени

П_н .( t ; f ) = n s ( t - c I f ; f )

Hcs при условии преобразования частотной формы сигнала Hcs, состоящем в модуляции его частот- ного спектра (в области его преобразования Фурье s(f)) согласно соотношению

( H c s )( f ) = e "² • ■ ^j c *'^{( f} f V s ( f ).

Каждое "гиперболическое" ВЧП относится к группе преобразований с комбинированным свойством ковариантности и может быть выражено в виде любого из трех соотношений (1), (2), (3). Каждое из этих соотношений отличается формой ядра — видом подынтегральной функции и областью интегрирования переменных, которые входят в структуру ядра 4):

₁ го го / р р \

H s ( t . f ) =7 J J Г H f ■ f I^х f oo V f f )

x< exp го го

=J J

- го - го

Ф H

( ln

2 n jtf - In

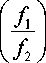
k s ( f l ) • s * ( f , ) • d f i d f 2 =

( f

V fr

V s ( b , в ) x

x { exp[2 n jtf в ] } • d b d в =                        ⁽²⁾

го го

= J J ^H (Z,в)• Bs (Z,в)x

-го -го x< exp

2 n j(tf в - Z ) ^ ln

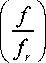
H d Z i d в 2 -

В выражениях (2) и (3) константа f_r ( f_r >  0) является фиксированным значением опорной, или нормирующей частоты, а в качестве ядер преобразования используются так называемые

— Г-произведение сигналов

V s ( b , в ) = f r • e b • s ( f r • e b ^{+ в I2} ) • 5 * (f • e b ^{- в 12} ); (3')

— Г-двойственная функция B_s ( Z , в ) (аналог двойственной функции, приведенной в систематизированной сводке, содержащейся в [6], [7]):

го

B s ( Z , в ) = J V s ( b , в ) • e ^{2 n j Z b} d b =

-го го                                          2njZ-lnI fl

= J s ( f • e ^{в I2} ) • s * ( f • e ^{в I2} ) • e      ^{V f}' V d f .       ⁽⁴⁾

• ⁴⁾ Отметим, что здесь используется преобразование Фурье так называемой аналитической формы сигнала со спектром только в области положительных частот, т. е. s ( f ) = 0 для f < 0.

  Двухпараметрические функции (ядра преобразований) Г_H ( b _1, b ₂), Ф_H ( b , β ), Ψ _H ( ζ , β ) полностью определяют Г-ВЧП. Характеризуя одно и то же ВЧП, они взаимно связаны соотношениями (5):

  
  

  Г H ( b l , b 2 ) =        Ф

  b ₁ b ₂

  
  

  - In Jb b , ln—

  12 b ₂

  
  

  to

  ^ H ( Z , в ) = J Ф н ( b , в ) e ² ' ^b d b .

  -to

  
  
  
  

  При обработке сигналов многие Г-ВЧП дают анализ с постоянным качеством на всей (интересующей нас части) время-частотной плоскости. Это свойство алогично вейвлет-преобразованию (и преобразованиям рассмотренной ниже группы аффинных ВЧП), в которых более высокие частоты анализируются с лучшим временным разрешением и худшим частотным разрешением, при этом площадь ячейки разрешения сохраняется одинаковой на всей плоскости время—частота [8], [9].

  К группе Г-ВЧП относится преобразование Q Альтес—Мариновича (Altes, Marinovich [10]), представленное соотношением (6), и преобразование P Бертрана (Bertrand [6], [11]), которое представлено соотношением (7):

  
  

  to (

  Q s ( t , f ) = J V

  -to V

  
  

  ln ^f , β f r ^,

  
  

  • e ^{2 n jtf в} d в

  
  

  to

  = f J S ( f • e ^в /2 ) • s* ( f • e ^{- в}/2 ) e ^{2 n jtf в} d в ;

  - to

  
  
  
  

  to

  ^I . f ) = J Vs

  -to

  
  

  In f - A p (в ) , e f_r

  
  

  • e ^{2 n jtf в} d в

  
  

  to

  = f J S ( f • G p (в ) e ^в/2 ) • s * ( f • G p (в ) e ^{- в}/2 ) x

  - to

  
  

  x G P ( в ) e ^{2 n} jtf ^в d в ,

  
  
  
  

  где G p ( в ) = -^/ 2^ ; A p ( в ) = - ln G p ( в ). sh( β / 2 )

  
  

  ядра Г-ВЧП. Любое Г-ВЧП обладает СК к одновременному изменению масштаба времени и частоты и к гиперболическому сдвигу времени. В качестве дополнительного СК будут рассмотрены несколько вариантов. Г-ВЧП с таким дополнительным свойством составляют подгруппу с новым названием, которое отражает вид дополнительного СК (ДСК) или специальное свойство ядра (в частности, его локализацию) ⁵⁾.

  Подгруппа, в которой в виде ДСК принято свойство ковариантности к простому сдвигу времени, условно может быть названа подгруппой аффинных Г-ВЧП ⁶⁾. С точки зрения свойств аффинные Г-ВЧП могут рассматриваться как пересечение аффинного класса преобразований с группой всех гиперболических ВЧП. Как увидим ниже, аффинные Г-ВЧП обладают также свойством локализации ядра, т. е. расположением значений ядра вдоль некоторой линии на время-частотной плоскости.

  Подгруппу, состоящую из Г-ВЧП с ДСК к степенной модификации временнóго сдвига, удобно назвать степеннóй подгруппой (относительно общей группы Г-ВЧП). Степеннáя подгруппа может считаться обобщением аффинной подгруппы: при временнóм сдвиге со степенью единица степенные гиперболические преобразования эквивалентны аффинным с точностью до выбора единиц измерения времени и частоты.

  Дополнительные свойства ковариантности (кроме основных, определяющих эту группу Г-ВЧП в целом) показаны в табл. 1 для Г-ВЧП аффинной и степенной подгрупп, а также для Г-ВЧП с локализованным ядром.

  ХАРАКТЕРИСТИКА ПОДГРУПП Г-ВЧП

  Особенностью преобразований сигнала из подгрупп Г-ВЧП является наличие у них помимо двух основных СК (ковариантности ко время-частотному масштабированию и к гиперболическому сдвигу времени) еще некоторого дополнительного свойства, которое определяет их специфику.

  
  

  РАЗНОВИДНОСТИ ГИПЕРБОЛИЧЕСКИХ ВРЕМЯ-ЧАСТОТНЫХ ПРЕОБРАЗОВАНИЙ

  В группе Г-ВЧП можно выделить несколько подгрупп, в каждой из которых ВЧП (кроме основного комбинированного свойства ковариантности) обладает некоторым дополнительным свойством ковариантности (СК) или особенностью

  
  

  • ⁵⁾    Последующий анализ относится к гиперболическим ВЧП, которые характеризуются свойством ковариантности к изменению масштаба и гиперболическому смещению времени. При анализе Г-ВЧП с дополнительными свойствами ковариантности (ДСК) для краткости будет использоваться термин "подгруппа", который подразумевает, что это "подгруппа Г-ВЧП с определенным ДСК".

  • ⁶⁾    Именно аффинные (время-масштабные вейвлет-) преобразования обладают ковариантностью к изменению масштаба и (простому) сдвигу времени.

  
  

Табл. 1. Дополнительные свойства у подгрупп гиперболических ВЧП и вид их ядра

Тип подгруппы	Дополнительные свойства		Ядро преобразования Ф н ( b , в )
Аффинные Г-ВЧП	H ss ( t , f ) = H ( t - т ; f ) при ( S r s )( f ) = e xp ( - 2 П j T f ) • s ( f )		B h ( в ) ’ 5	f b - 1nS h ( в /2) ) V        в /2 )
Степенные Г-ВЧП	HD ( k ,. ( t , f ) = H ( D c s при т k ( f ) = у r f ( Dk ) s )( f ) = exp V	t - c T k ( f ); f ) / X k -1 f f ) 1 , V Jr ) f f ^ k) - 2 п jc yl • s ( f ) V fr J )	B h ( в ) ’ 5	f,    1 , sh( k в /2) ) b • ln V k     k в /2 )
Г-ВЧП с локализованным ядром	H e ( t , f ) = r 2( f ) • 5 ( t - c • Ц '( f ) ) при s c ( f ) = r ( f ) • e xp ( - 2 п jc ^ ( f ) )		B h ( в ) ’ 5 ( b - A h ( в ) ) (при дополнительных условиях)

Подгруппа Г-ВЧП с дополнительным СК к простому (независимому от частоты) смещению времени

Если неизвестно, является ли при распространении сигнала в неоднородной среде его задержка (временное смещение) частотно-зависимой, и форма время-частотного распределения сигнала близка к гиперболической, то для корректного анализа такого сигнала желательно, чтобы его Г-ВЧП имело дополнительное СК к простому (независимому от частоты) смещению времени. Подгруппа ВЧП с таким СК должна обладать свойствами ковариантности к масштабированию, гиперболическому смещению времени и к постоянному временному смещению. У преобразований из этой подгруппы двумерное ядро обычных Г-ВЧП выражается как произведение двух одномерных ядер.

Подгруппа Г-ВЧП с локализацией ядра

Не менее важна подгруппа Г-ВЧП с локализованным ядром ⁷⁾. Подгруппа состоит из всех Г-ВЧП, у которых ядро Ф _H( b , в ) из (2) локализовано вдоль кривой b = A H ( в ) на плоскости ( b , в ), т. е. оно может быть представлено в форме соотношения (8):

Ф н ( b , в ) = B h ( в ) • 5 ( b - A h ( в )),      (8)

где A_H ( в ) и B_H ( в ) ^ 0 — произвольные функции. С учетом того, что (8) влечет ^ _н ( д , в ) = = B_H ( в )exp ( 2 п j g A H ( в ) ) в (3), подстановка (8) в (2) позволяет выразить локализованное ядро в соответствующей подгруппе Г-ВЧП в виде:

H ( t , f ) =

= J V ln f - A h ( в ); в )’ B h ( в )exp(2 п jtf в )d в =

• - J V J r             J

= f J s | f exp ^f- A h ( в ) + ; ))x

• - J V V           2 ) )

xs* Г f exp f-Ah (в) - |))’ Bh (в) ’ e"AH(в) x xexp(2 п jtf в )dв.

Двумерное ядро у Г-ВЧП этой подгруппы может быть выражено через две функции A H ( e ) и B H ( e ) ("одномерные ядра"), которые полностью характеризуют определенное ими преобразование с локализованным ядром.

Преобразования из подгруппы с локализованными ядрами полезны для анализа сигналов с определенной спецификой время-частотного распределения. В частности, можно рассмотреть семейство сигналов, которые в частотной области

Табл. 2. Одномерные ядра-компоненты для преобразований сигнала подгруппой Г-ВЧП с локализацией ядра

Вид преобразования	Одномерные ядра-компоненты в соотношении (9)
	A H ( β )		B H ( β )
Преобразование Альтес—Мариновича	0		1
Преобразование Бертрана	In	^ sh( в /2 ) < в /2 )	1
Преобразование Папандреу—Супапола	1 ln k	' sh( k в /2 ^ ( k в /2 J	1
Обобщенное степеннóе преобразование с масштабированием частоты Q s ˆ ( α ) ( t , f )	α β		1

имеют вид s c ( f ) = r ( f ) • exp[ - 2 n jc q ( f )], положительную амплитуду r ( f ), фазовую функцию ξ ( f ), константу с и функцию групповой задержки т ( f ) = c ^ '( f ) • Для такого семейства сигналов при определенных условиях ⁸⁾ может быть определено Г-ВЧП, которое будет хорошо локализоваться (концентрироваться) вдоль кривой, определяемой частотной зависимостью групповой скорости c ^ '( f ), т. е. преобразование вида H - ( t ; f ) = = r ² ( f ) • 5 ( t - c l '(f ).

Преобразования подгруппы с локализованным ядром служат концептуальной основой для некоторых важных Г-ВЧП, включая те, которые относятся к аффинной подгруппе или к подгруппе степенных Г-ВЧП. Известные преобразования подгруппы с локализованным ядром — это преобра- при Вн(в)=

r ²( f ) R f , β ( A H ( β ))

> 0.

зование Q_{s ˆ} ( t , f ) Альтес—Мариновича (6), преобразование P_{s ˆ} ( t , f ) Бертрана (7), преобразование Папандреу (Papandreou) [14] и анализируемое ниже обобщенное степеннóе распределение с масштабированием частоты Q_{s ˆ} ^{( α )} ( t , f ). Одномерные ядра, произведением которых могут быть представлены двухпараметрические ядра этих преобразований, показаны в табл. 2.

Аффинная подгруппа

Общим требованием к преобразованиям аффинной подгруппы (кроме общих СК, свойственных для Г-ВЧП) является наличие дополнительного СК к постоянному (частотно-независимому) сдвигу времени. Поскольку весь анализ производится для частотной формы сигнала, т. е. его ПФ 9), то с учетом того, что сдвиг сигнала по времени соответствует фазовому множителю у его ПФ, дополнительное свойство ковариантности, определяющее аффинную подгруппу, выражается соотношениями:

H s ₅ ( t , f ) = H s ( t - т ; f )

при ⁽ S r^{S )} ( ^f ) = exp ^{( - 2 П} j ^{T f} ) • s ^{( f} )•

Обладая свойствами ковариантности к временному сдвигу сигнала, к масштабированию и к гиперболическому (частотно-зависимому) сдвигу времени, преобразования аффинной подгруппы

Г-ВЧП относятся к общему аффинному классу — к классу преобразований, который включает не только аффинные Г-ВЧП, но и (аффинные) время-масштабные преобразования типа вейвлет-пре-образования и общего преобразования Бертрана 10). Фактически подгруппа аффинных Г-ВЧП принадлежит пересечению множества общих преобразований аффинного класса и множества (за счет многообразия формы ядра) преобразований из группы гиперболических ВЧП 11).

Наличие у Г-ВЧП свойства ковариантности к простому сдвигу времени эквивалентно выполнению специального условия. Это условие получается подстановкой (2) в (10) и имеет форму соотношения (11):

Ф н ( b , в ) • exp{ - 2 п jt в [ e ^- b ( e ^{в /2} - e ^{- в /2} ) - в ]} = = Ф н ( b , в ) при V t , b , в .

Выполнение (11) возможно только при равенстве нулю экспоненты слева, поэтому условие переходит в более простую форму e- b (eв/2

e в/2) - в = 0, эквивалентную b = ln

sh( в /2) в /2

.

Последнее выражение определяет явную зависимость b от в и означает, что для ядра Фн (b, в) преобразования аффинной подгруппы Г-ВЧП тре- буется выполнение условия b = ln sh( в /2) в/2

, ко-

торое в свою очередь приводит к ядру со своеобразной формой локализации:

Ф н ( b , в ) = B h ( в ) • 5 ( b - A p ( в )),

где A P ( в ) = ln

sh( в /2) )

в/2 I;   вн(в>    произволь- ная функция12).

Таким образом, только Г-ВЧП, имеющее ядро Фн (b, в) с формой по выражению (12), обладает свойством ковариантности (10) (к частотно-независимому смещению времени) и принадлежит к аффинной подгруппе. Сравнение выражений (12) и (8) показывает, что аффинные Г-ВЧП принадлежат также и подгруппе Г-ВЧП с локализованными ядрами. Кроме того, комбинация выражений (9) и (12) позволяет получить общий вид (13) для Г-ВЧП аффинной подгруппы:

H ( t , f ) =

ГО

= f J 5 ( fGp ( в ) e ^{в /2} ) • 5 * ( fG p ( в ) e ^{- в /2} ) x - ГО

X G p ( в ) • В н ( в ) • exp(2 п jtf в ) d в ,        (13)

где G p ^{( в} ) = _sh в ^ 22) = e~^{A p ( в} ) ; b h ^{( в} ) ^— произ вольная функция от в . Следовательно, преобразования аффинной подгруппы Г-ВЧП характеризуются только однопараметрическим ядром В_н ( в ).

Используя соотношение (13), можно показать, что любое преобразование аффинной подгруппы Г-ВЧП можно выразить через Г-ВЧП Бертрана (7) в виде свертки (14), включающей операцию масштабирования временной переменной:

ГО

H ( t , f ) = f J Ь н ( f ( t - t ') ) • P ( t ', f )d t ',     (14)

-ГО где bH (c)— обратное преобразование Фурье от Вн (в )13).

Степеннáя подгруппа

Концепция аффинной подгруппы Г-ВЧП модифицируется при рассмотрении более сложной формы частотной зависимости функции групповой задержки, которая для частотной формы сигнала имеет вид т ( f ) = c ^ '( f ) и рассмотрена выше для преобразований подгруппы с локализованными ядрами. По такому принципу введения усложненной формы зависимости т ( f ) формируется степенная подгруппа Г-ВЧП. Ее преобразования характеризуются дополнительным параметром к . Причем, кроме свойства ковариантности к масштабированию (обычному СК для всех Г-ВЧП), преобразования степенной подгруппы имеют СК к "степенному сдвигу времени":

H D k ) . ( t , f ) - H - ( t - C T k ( f ), f ) при ( D Ck ) - )( f ) = e "2 ⁽ f ) - ( f ),

k

k - 1

где 1. (f) -I fl ; tk (f) = -d 1. (f) = k I fl V Jr J df Jr V Jr J при f > 0 и k ^ 0 .

Оператор D_c ^{( k )} является фазовым фильтром со степеннóй зависимостью для функции групповой задержки τ _k ( f ) для сигнала в частотной форме. При значении параметра k = 1 преобразования сте-пеннóй подгруппы просто относятся к аффинной подгруппе Г-ВЧП. При других значениях параметра k степеннáя подгруппа состоит из Г-ВЧП, удовлетворяющих СК к степеннóму сдвигу времени в соответствии с соотношениями (15). Такое свойство преобразований полезно при анализе сигналов, распространяющихся в среде с частотно-зависимым рассеянием или поглощением.

Преобразования степеннóй подгруппы при определенных условиях могут иметь локализованную форму ядра (т.е. относиться одновременно и к подгруппе с локализованными ядрами, описываемыми соотношением (9)). Так, если у преобразования с локализованной формой ядра (9) однопараметрические ядра AH(β)и BH(β) будут иметь форму где bH (c) — обратное преобразование Фурье от BH(β).

ОБЩИЕ СВОЙСТВА Г-ВЧП

Кроме характеристики каждой из подгрупп гиперболических ВЧП, (с точки зрения теории вре-мя-частотного анализа нестационарных сигналов ИИС) большое значение имеют общие свойства Г-ВЧП. Главные среди этих свойств: обратимость ядер преобразования; сохранение нормы и внутреннего произведения Г-ВЧП (и произведения соответствующих ядер) 14). Второе из этих свойств равносильно справедливости формулы Мойела [15], [16]. Обратимость означает, что при преобразовании отсутствуют существенные потери информации относительно сигнала.

Обратимость Г-ВЧП на уровне ядра

Согласно соотношениям (1)–(3), Г-ВЧП H_s ( t , f ) выражается с помощью специального линейного преобразования через двухпараметрические ядра V ₅ (b , в ) и B - ( Z , в ) • При определенных условиях обратимости Г-ВЧП (свойства регулярности) ядра могут быть представлены выражениями (18):

A h ( в ) = 1ln k

" sh( k в /2) ) , _V k в /2 J ;

L L    /

V - ( ^b , в ) - J J Ф н ^b - ln

-L 0

f , в l" H - ( t , f ) X ^fr J

B _H ( β ) — функция произвольного вида,

X exp( - 2 n jtf ) • d t d f ,

то это преобразование будет одновременно относиться к степеннóй подгруппе. С учетом такой взаимосвязи можно считать, что степеннáя подгруппа является частью подгруппы Г-ВЧП с локализацией ядра. Условием принадлежности преобразования (9) к степеннóй подгруппе является специальная структура его однопараметрических ядер в форме выражения (16). Таким образом, любое преобразование степеннóй подгруппы, имея фиксированную форму однопараметрического ядра A_H ( β ), характеризуется только формой ядра B_H ( β ).

Особое место в степеннóй подгруппе занимает преобразование P - ^{( k} ) , у которого в (16) B_H ( в ) = 1. Роль этого преобразования в степеннóй подгруппе такая же, как у преобразования P_s в аффинной подгруппе. Любое преобразование степеннóй подгруппы может быть представлено в виде свертки P_{s ˆ} ^{( k )} с масштабированием временнóй переменной:

b- (Z, в ) =

L

= ^ H ¹ ( Z , в ) J - L

L

J ^_H ( Z , в ) • H - ( t , f ) X

f x exp -2n j(tf в - Z " ln—

2,

где обратные ядра Ф -^- ( b , в ) и ^ H ( Z , в ) взаимосвязаны соотношением

L

^H (Z, в) - J ФН1 (b, в) Фн (b, в)" e(2П jZ b) • db .

-L

В свою очередь зависимости между обратными ядрами и прямыми ядрами выражаются двумя соотношениями (19):

ГО

J Ф Н ( b - b ', в ) • Ф н ( b ', в ) • d b ' = 5 ( b ),

- ГО

ГО ГО

Н . ( 0 ) = J J L hh ( 0 ; t ', f ') • H s ( t ', f ') • d t 'd f ', (21)

- ГО 0

'V ( Z , в И н ( Z , в ) = 1.

Одним из преобразований15), удовлетворяющих (19), является обобщенное преобразование Бертрана (7), для которого выполняется также и формула Мойела.

Из существования обратимости вытекают некоторые результаты относительно структуры Г-ВЧП.

1) При обратимости преобразований на уровне ядра сигнал может быть восстановлен с точностью до постоянного сдвига фазы. Для этого по (18) вычисляется V s ( b , в ), после чего из (3') следует, что сигнал (с точностью до неизвестного сдвига фазы ф ) определятся на основе выражения для V s ( b , в ) по соотношению

где ядро L HH ( 0 ; t ', f ') определяется выражением

ГО ГО

L hh ( 0 ; t ', f ') = J f К н ( 0 ; fe ^{в /2} , fe ^{- в /2} ) x 0 - ro

x ФН¹

In f ; в L e"^{2 n} f

• d f d в .

Если билинейное представление сигнала¹⁶⁾ Н %^( 0 ) является само гиперболическим ВЧП, то (21) имеет более простую форму (22):

H s ( t , f ) =

s ( f ) =

V s (ln ff ;ln f )

Jr     f , ej f • Vs (In f ;0) f

ГО ГО       /                     Z» \

= JJ Х нн tf - t' f ';in f 1. H s ( t\ f ') • d t 'd f ', (22)

- ro 0      V               ^f J

■ ro 0

где ro ro

Х нн ( c , b ) = J J Ф н ( b - b '; в ) • Ф Н (b '; в ) • e ^{2 n} d b 'd в .

- ro - ro

где f выбирается произвольно при условии, что л

V (ln f ;0) * 0.

2) При обратимости Г-ВЧП любое (билинейное) представление сигнала Н ( 0 ) может быть получено с помощью линейного преобразования

ГО ГО

Н ( 0 ) = JJ К н ( 0 ; л , f 2 ) • s ( X ) • s * ( f , ) • d f 1 d f 2 , (20) 0 0

где 0 — двумерный вектор параметров (таких как ( t , f) в случае Г-ВЧП); K H ( 0 ; f, f , ) — ядро, характеризующее преобразование Н^ [17].

Использование выражения для s ( f ) • s * ( f , ) (из соотношения (3')) в (20) показывает, что преобразование Н ( 0 ) может быть выведено из обратимого Г-ВЧП H s ( 0 ) с помощью линейного преобразования в форме соотношения (21):

3) Для обратимого Г-ВЧП линейное преобразование сигнала порождает линейное преобразование Г-ВЧП. Если Н — обратимое Г-ВЧП, то билинейное ВЧП H s ,( t , f ) линейно преобразованного сигнала (в частотной форме) вида $ f ) =

ГО

= J T ( f , f ') s ( f ')d f ' имеет линейно преобразован- 0

ное Г-ВЧП первоначального сигнала:

ro ro

H s „( t , f ) = J J L th ( t , f ; t ', f ') • H s ( t ', f ') • d t 'd f ',

- ГО 0

где

ГО ГО ro ro

L TH ( t , f ; t ', f ') = f J J J T ( f 1 e ^/ ² ; f _; e ^в 2 ^/2 ) x 0 - ro 0 - ro

x T * (Л e ^{- в} - ^/2 ; f 2 e ^{- в} 2 ^/2 ) x Ф т

in f ; в • Ф ^-1 in f ²; в₂ x ¹ т           ’^/^²

J\ J V f 7

x exp[2 n j (tf в 1 - 1 ' f ' в 2 )] • d f 1 d в 1 d f _£d в 2 .

Все соотношения этого раздела получены Хла-ватчем (Hlawatsch) [17]. Формализация характера изменения обратимого Г-ВЧП при линейном пре- образовании сигнала, рассмотренная в 3), может служить основой для получения свойств ковариантности.

4) При обратимости Г-ВЧП базис пространства сигналов¹⁷⁾ может быть модифицирован в двумерный базис для этого преобразования. Если { У_к ( f )} _к = ₁₂ N — это набор линейно-независимых сигналов (набор полный в L₂), т. е. базис пространства сигналов, и если Н — это обратимое Г-ВЧП, то соответствующий набор гиперболических ВЧП от авто- и кросскорреляционных функций (АККФ) этих { у_к ( f )} _к = ₁₂ N является двухпараметрическим базисом для совокупности всех время-частотных представлений сигнала. С помощью набора ^{ H аккф< у.у k ) } , к = 1,2,..., n можно предста вить любое время-частотное преобразование ¹⁸⁾ сигнала в виде линейной комбинации. Такая форма разложения время-частотного представления сигнала используется при решении задач оптимизации ВЧП [18-20].

Свойство обратимости Г-ВЧП для подгруппы с локализованным ядром

В отдельных подгруппах Г-ВЧП, которые характеризуются дополнительными свойствами ковариантности, вычисление обратных ядер производится с помощью более простых соотношений. Обратные ядра для обратимого Г-ВЧП с локализованным ядром определяются соотношениями (23):

Ф"^нЧb , в ) = L ⁵ ( b + A h ( в ) ) , B H ^{( в} )

^ H ( Z , в ) = -4-exp[ - 2 п j Z A h ( в )], b h ^{( в} )

где А_н ( в ) и B_H ( в ) определены в (8). Для обратимости преобразования Н требуется условие B_H ( в ) ^ 0, а А_н ( в ) может быть произвольным.

Если Н и НН относятся к подгруппе Г-ВЧП с локализованными ядрами и Н обратимо, то ядро Х нн , преобразующее Н в Н , согласно (22), имеет более простую форму:

^Л Нн ⁽ c , b )

⁷ B& ( в )   /                     х

= [ /^ •5 (b - [ Ан (в) - Ан (в )1)х

-7 ^ВН ^{( в} )

х exp(2 п jc в ) • d в .

При условии А н ( в ) = А_н ( в ), которое может удовлетворяться в аффинной или степенной подгруппах Г-ВЧП, преобразующее ядро Л н еще более упрощается, и оно выражается зависимостью:

ЛНн (c, b) = юНн (c) • 5 (b)’ где ωH%H

B % ( в )

B h ( в )

• exp(2 п jc в ) • d в .

Одновременно соотношение (22), выражающее взаимосвязь преобразований Н и НН , тоже приобретает в этом случае более простую форму свертки с масштабированием (24):

Н ( t , f ) = f J ® Нн ( ( f ( t - 1 ') ) • H ( t ', f ) • d t '. (24)

Свойство обратимости Г-ВЧП аффинной и степеннóй подгрупп

Аффинные Г-ВЧП составляют часть подгруппы гиперболических преобразований с локализованным ядром, поэтому обратные ядра Ф Н ( b , в ) и *E H ( Z , в ) у обратимых преобразований аффинной подгруппы, как видно из (23), определяются соотношениями

Ф »( b , в ) =        5 ( b + А р ( в ) ) ,

B H ^{( в} )

^ Н *( Z , в ) = -4-exp[ - 2 п j Z А р ( в )1, b h ^{( в} )

л zox j | sh(в/2) ] т               , где Ар(в) = lnI —в/2— |. (При этом преобразование Н обратимо, только если BH (в) не обращается в нуль).

С помощью обратимого аффинного Г-ВЧП Н любое другое преобразование той же подгруппы может быть выведено с помощью операции свертки с масштабированием (24).

Анализ, проведенный для Г-ВЧП аффинной подгруппы, применим и для степенной подгруппы, за исключением того, что выражение А_р ( в ) для однопараметрического ядра у обратимых Г-ВЧП степенной подгруппы заменяется на

А_Р <  к ) ( в ) = ¹ • ln

Pk

sh( к в /2) к в /2

Формула Мойела, ограничения на ядро и обратимость ядер

При определенных условиях линейные преобразования, лежащие в основе выражений (1-3) для Г-ВЧП, сохраняют величину внутреннего произведения 19):

(H , H = V- , V ) и ( H , H \ = B, , б. V

\    51       5 2 /     \ 51     5 2 /        \    51       5 2 /     \   51     5 2 / где V5 (b, в) и V (Z, в) определены выражениями (3') и (4).

Свойство сохранения внутреннего произведения (СВП) в другой форме эквивалентным образом выражается соотношением (H , Н₅ 2) = = | ^1 , s ₂) |² , которое называется формулой Мойела [21, 22]. Частный случай формулы Мойела дает связь нормы сигнала и его Г_ВЧП: 11 Н₅ 11 = 11 5 11.

К преобразованиям с СВП относятся Г-ВЧП Бертрана (7) и обобщенное преобразование to        ( ¹ - а I в            4¹ + а I в

Qа)(t, f) = f 'J 5( f • e12 J ) • 5( f • e 12 J ) • e"ав x -to x e2njtfвjp — Г-ВЧП, которое характеризуется свойством ковариантности к степенной деформации обеих переменных. Для преобразований этой подгруппы СК выражается соотношением

Хлавачем показано, что для выполнения свойства СВП требуется наложить на ядра Г-ВЧП ограничение в форме (25):

to

J    Ф Н ( b ' - b , в ) • Ф н ( ь ', в )d b ' = 8 ( b );

-to

V Н ( Z , в ) • V н ( Z , в ) = 1.

Сравнение (25) и (19) показывает, что Г-ВЧП с СВН является обратимым. Обратные ядра такого преобразования достаточно просто определяются через прямые ядра:

Ф Н *( b , в ) = Ф Н ( - b , в ) и V н\ Z , в ) = V Н ( Z , в ).

Г-ВЧП с СВП обладают некоторыми дополнительными свойствами.

1) Квадрат модуля любого билинейного представления сигнала ( Н ¹ ( 0 ) из (20)) может быть выражен как квадратичная форма:

to to to to

1⁷ H₅ ( °)|     J J J J H * ( t , f ) • L HH ( t , f ; t ', f ') x

-to 0 -to 0

x H 5 ( t ', f ') • d t d f d t 'd f ', ⁽ 26)

Н 5 ( t , f ) = H

при ⁽ P a ^{5 )( f} ) ⁼

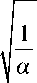
α t

V f

( f

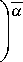
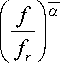
где H — произвольное Г-ВЧП с СВП, а L HH (t , f ; t ', f ') определяется соотношением (27):

L HH ( t , f ; t ', f ') =

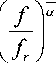
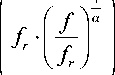
a > 0.

to to to to

= J J J J Kh ( ® ; f 2 e ^{в 2/2} , f 1 е ^{в 1/2} ) x

0 -to 0 -to

x K H ( 0 ; f 2 e ^{- в} 2 ^/2 , f ] e ^{- в} - ^/2

^x Ф Н

Г 1

In f , в • Ф_H

1 H

V ^f 1     V

f ' „1 ln —, в ₂ |x

• ¹⁹⁾ Внутренние произведения ^^ (являющиеся в функциональном анализе (ФА) эквивалентом скалярного произведения) определяются в виде

to

5 1 ,й) = f 5 ( f ) 5 * ( f )d f 0

для произведения сигналов в частотной форме и в виде ; Н1, Ну = J J Н1(t, f) • Н2* (t, f) dt df для произве--to 0

дения Г-ВЧП. В соответствии с этим определяются значения норм || 5|| и || Н ||     соотношениями to                                                   toto

|| 5 1|²=( 5 , 5 ) = J1 5 ( f ) |² d f и || Н ||= н , H = J J| н ( t , f )|²d tdf . 0                                                   -to 0

Для свойства сохранения нормы в ФА (и реже в области теории обработки сигналов) используется термин "унитарность".

x e ^{2 n} j^{( tf в} 1 ^- гг ^в 2 > d f 1 d в . d f , d в ₂.

где, как и в (20), 0 — двумерный вектор параметров (таких как ( t , f l); K H ( 0 ; f _? f , ) — ядро, характеризующее преобразование НН .

• 2 ) Для Г-ВЧП, обладающего свойством СВП, базис пространства сигналов образует соответствующий этому преобразованию базис. Если набор { 5к ( f )} _k = 12 N служит базисом для сигналов, то двухпараметрическим базисом для Г-ВЧП Н с СВП может служить набор Н -преобразований от авто- и кросскорреляционных функций (АККФ), образованных из базисных функций сигналов, т. е. набор ^{ H аккф 5 _ ,5 , ⁽ t , ^{f )}} ,. j = 1,2,... является базисом

Н -преобразования. При этом можно говорить, что базис сигналов индуцирует базис для Г-ВЧП с СВП.

• 3 ) Существует задача определения вида сигнала, для которого ВЧП H_{s ˆ} ( t , f ) наиболее близко к некоторой заданной форме время-частотного распределения (ВЧР) — "модели" ВЧР M ( t , f ). Такой условно "оптимальный" сигнал s ˆ _{опт .} оценивается на основе обобщенного принципа наименьших квадратов: s опт ( f ) = arg min 11 M - H_s 11. Соответ- ^. s ˆ

ствующий метод разработан Боудри-Бартелсом и Парксом (Boudreaux-Bartels, Parks) [20] и используется для улучшения качества время-частотного представления компонент сигнала [23]. Если преобразование H_{s ˆ} является Г-ВЧП с СВП, то определение оптимального сигнала s ˆ _{опт .} осуществляется следующим образом [24].

• •    К модели ВЧР — M ( t , f ) — применяется преобразование (18):

to to

V% ( b , в ) = ff Ф Н

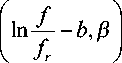
■ M ( t , f ) ■ e ^{-n jW} d t d f.

• •    Функция V%(b , в ) преобразуется в

j ( f i , f 2 ) =-777 vfin V

N ^f 1 ^f 2 V ^f r

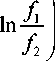
• •    Создается комбинация, инвариантная к комплексной сопряженности, (операция "эрмитиза-ции"):

J эрм . = 2[ J ( f i , f 2 ) + J ( f , f _£)]-

• •    Для J_эрм{f i , f 2 ) вычисляется максимальное собственное число λ 1 и соответствующая собственная функция E 1 ( f ) с использованием соотношения собственного числа λ k и собственной функции E k ( f ):

to f Jэрм.( fi, f2) ■ Ek (f2)df2 = ^kEk (fi). 0

• •    Определяется "оптимальный" сигнала s опт (с точностью до постоянного сдвига фазы ϕ ˆ ) по соотношению:

Sonm.(f) = Ae2n*E1(f) при Xi > 0 и sопт.(f) = 0 при Xi ^ 0-

По описанной схеме определяется, в частности, оптимальный сигнал .? _опт ( f ) = arg min 11 M - Q s 11

для модели ВЧР M ( t , f ) и Г-ВЧП Q_s Альтеса— Мариновича (6). Для этого используется ядро

J (fi, f2) = to

to

= [ M ⁽ t , V j \ , ^f 2 ) ■ exp ^{- 2 П} j^ ^fX , ^f 2 ■ lnv ■ d t . f

-to                            _                          J 2 _

2 _

to

Полезно отметить, что для Г-ВЧП из аффинной, степеннóй подгрупп и для преобразований с локализованным ядром свойство СВП выполняется только при условии | B H ( в ) | = i, или, что рав-

1 ноценно,

B H ( β ) ничений нет.

= B * ( в )- На ядро A h ( в )

H

огра-

ЗАКЛЮЧЕНИЕ

Рассмотрены элементы теории время-частот-ных преобразований (ВЧП), применяемых для анализа и интерпретации нестационарных сигналов в ИИС. Проанализирована концепция ковариантности — свойства модификации параметров преобразования (координат двухпараметрического представления результата ВЧП сигнала на время-частотной плоскости), модификации, которая вызвана преобразованием переменной во временнóй или частной форме сигнала. Основная группа ВЧП, многообразие которой анализируется в рамках концепции ковариантности, — это группа преобразований, которая получается на основе свойства ковариантности к одновременному масштабированию времени и частоты, а также удовлетворяет свойству ковариантности к ("гиперболически ") частотно-зависимому сдвигу по времени. Эта группа условно называется группой гиперболических время-частотных преобразований (Г-ВЧП). Анализ проведен для частотной формы сигналов, которая использована и в аналитических соотношениях для Г-ВЧП.

• •    В группе Г-ВЧП выделено несколько подгрупп, в каждой из которых ВЧП (кроме основного комбинированного свойства ковариантности) обладает некоторым дополнительным свойством ковариантности (СК) или особенностью ядра Г-ВЧП. В качестве носителей дополнительного СК анализируются несколько типов преобразований. Г-ВЧП с такими дополнительными свойствами составляют степеннýю и аффинную подгруппы и подгруппу с локализованным ядром.

• •    Для степенной и аффинной подгрупп и для подгруппы с локализованным ядром показана взаимосвязь дополнительного свойства ковариантности со структурой ядра Г-ВЧП. Систематизированы свойства преобразований и их особенности в каждой из подгрупп.

• •    Рассмотрены общие свойства преобразований: обратимость Г-ВЧП на уровне ядра (с дифференциацией для каждой из подгрупп); инвариантность внутреннего произведения; формула Мойела и связанные с ней ограничения на ядро и на обратимость ядер преобразования.