Классификация бинарных квазиканонических систем счисления в мнимых квадратичных полях

В основе представления и обработки информации в современных компьютерах лежит бинарная система счисления поля действительных чисел. Среди других систем счисления, которые используют всего две цифры для представления каждого элемента рассматриваемой алгебраической структуры, наиболее исследованы канонические системы счисления (КСС) квадратичных полей. Они являются естественным обобщением степенного представления обычных целых чисел [1] на случай алгебраических целых чисел. Такие системы счисления рассматривались ещё в монографии Кнута [2], но систематическая разработка теории КСС началась в работах И. Катаи и Я. Сабо [3], Б. Ковача [4], И. Катаи и Б. Ковача ([5], [6]), У. Дж. Джилберта [7] и других исследователей.

Понятие КСС впервые появилось в работах Катаи и Сабо [3], где были указаны все целые гауссовы числа, являющиеся основаниями КСС. Этот результат был обобщён на случай квадратичных целых чисел в работах Катаи и Ковача [5], [6], а также независимо от них в работе Джилберта [7].

Среди приложений КСС следует отметить работы, касающиеся связи фракталов и КСС [8 11]. Эта связь рассматривалась и в других работах [12–16]. Некоторые авторы исследовали фрактальную структуру границ [17–20] и динамические свойства [21] фундаментальных областей КСС. Более того, в работах [11], [22], [23] рассматривалась связь мозаик, а следовательно, и КСС с вейвлетами.

Системы счисления, в которых вместо целых рациональных чисел, образующих множество цифр КСС, рассматриваются целые квадратичные числа, изучены в меньшей степени. Такие системы счисления будем называть квазиканоническими.

В настоящей работе исследуются все бинарные ква-зиканонические системы счисления в кольцах целых чисел мнимых квадратичных полей. Для каждой из этих систем счисления рассматриваются алгоритмы реализации основных арифметических операций.

где d – целое число, свободное от квадратов. При d >  0 квадратичное поле называется вещественным, а при d <  0 - мнимым.

Определение. Если у элемента z = a + b^ е Q (V d ), его норма Norm ( z ) и след Tr ( z ) есть целые числа:

то

Norm(z) = (a + b/d)(a - bVd) = a2 - db2 е Z, Tr(z) = (a + bVd) + (a - b/d) = 2a е Z, этот элемент называется целым алгебраическим числом поля Q( d) [25].

Сформулируем ряд известных утверждений о целых алгебраических числах.

Утверждение. Пусть d <  0, А = | d |. Тогда целыми алгебраическими числами мнимого поля Q ( i VA )

являются числа

I a + bi VA ; a , b е Z при A = - 2, - 3 ( mod 4 ) ;

z = 5      1                                                .

; a , b е Z при A = - 1 ( mod 4 ) .

Кольцо целых элементов поля Q (Vd) будем обо- значать S (Vd), а Z (Vd) — множество

z (Vd ) =

= { z = a + b/d : a, b е Z} c S (Vd) c Q (Vd).

Определение.   Целое алгебраическое число a = A±Vd (приd = 2,3(mod4)) или a = 2(B±dd) (при d = 1( mod 4) ) называется основанием КСС в кольце S (Vd) целых элементов поля Q( d) , если любой целый элемент этого поля однозначно представим в форме конечной суммы k(z)

z = £ ajaj , j=0

Канонические и квазиканонические системы счисления. Основные определения

Пусть Q ( d ) есть квадратичное поле [24]:

Q(Vd) ={z = a + bVd; a, bе Q}, aj е I = {0,1,...,|Norm(a)|-1} .

Пара {a;I} называется канонической системой s (Vd)

счисления в кольце

, а I – алфавитом этой сис- темы [25].

В исследованиях различных авторов, рассматривающих КСС, для представления целого алгебраического числа применяется рекуррентный алгоритм [26]. Однако с той же целью можно использовать и деление с остатком, реализуемое лишь в некоторых кольцах [21]. В настоящей работе рассматриваются только мнимые кольца.

Определение. Говорят, что в кольце D имеет место алгоритм деления с остатком, если на отличных от нуля элементах ре D определена функция ЦрЦ ,

ставление числа у ₀ является конечным, то есть процесс деления с остатком:

у0 = у 'а + r0,

у, = у2 -а+r,

принимающая целые неотрицательные значения, так, что выполняются следующие условия:

• 1) . если р^ 0 делится на а, то ||р||>||а||;

• 2) . для любых элементов в и а # 0 в D существуют такие у и r , что в = ау+ r , причём либо

r = 0 , либо || r || < ||а||.

....................., уi =уi+1 'а+r, где r0, r1,.., rl е I, конечен. Другими словами, существует такое I, что уl+1 = 0, а для этого, в свою очередь, достаточно, чтобы Norm (уm+1 )< Norm (уm) Vm = 0,1,..., I.

Определение. Системы счисления { а ; I } и { а‘ ; I 3 в кольце S ( 4d ) называются эквивалентными, если существует взаимно однозначное отображение

Утверждение. Среди колец

s (4d)

целых элемен-

тов мнимых квадратичных полей Q (V d ) алгоритмом деления с остатком по норме обладают те и только те, для которых d равно одному из следующих пяти значений: { - 1, - 2, - 3, - 7, - 11 } [24].

Стоит отметить, что числа у и r в равенстве в = ау+ r определяются неоднозначно, поскольку

существует несколько различных остатков r , имеющих одну и ту же норму. Это позволяет рассматривать различные системы счисления с одним и тем же основанием а , но разными алфавитами (множествами цифр).

Бинарные квазиканонические системы счисления

Рассмотрим все возможные бинарные системы счисления в кольцах целых алгебраических чисел мнимых квадратичных полей.

Определение. Квазиканоническая система счисления с основанием а и алфавитом I называется бинарной системой счисления, если Norm ( а ) = 2 и алфавит I состоит из двух цифр.

Отметим легко проверяемые свойства, которые справедливы для всех бинарных квазиканонических систем счисления.

Свойство 1. Согласно определению деления с остатком по норме и учитывая, что Norm ( а ) = 2, получаем

= (М«

^У 2 ’

где а - число, сопряжённое а .

Соотношение (1) следует из формулы в = ау+ r ,

которая встречается в определении деления с остатком.

Свойство 2. Если для пары { а ; I } доказано, что представление произвольного целого алгебраического числа у ₀ в форме у ₀ =у 1 а + r ₀ единственно, где r ₀ е I , то для того чтобы пара { а ; I } образовывала систему счисления, достаточно показать, что пред-

f : S (V d ) ^ S (V d ) , причём f ( I ) = I' , такое, для любого числа уе S ( Jd ) , представимого в

N теме счисления {а; I} в виде у = ^ apаp , p=0

что

сис-

где

a p е I , число f ( у ) в алфавите { а‘ ; I 3 записывается

N в виде f (у) = ^ f (ap) (а‘)p . Стоит отметить, что а’ p=0

необязательно равно f ( а ) .

Свойство 3. Если для у ₀, представимого в системе счисления { а ; I } , справедливо равенство у ₀ =у 1 а + r ₀, то, умножая это равенство на r^k , где r – первообразный корень из единицы степени, равной количеству единиц поля в кольце S (V d ) , получим, что число у ₀ r k имеет такую же запись в системе счисления { а ; I • r^k } , как и у ₀ в системе счисления { а , I } , то есть если

NN у0 = ^ ap аp , то у0 rk = ^ (aprk) аp . Эго означает, что p=0                        p=0

системы счисления { а ; I } и { а ; I • r^k } эквивалентны.

Аналогично, если взять сопряжение от обеих частей равенства у ₀ =у 1 а + r ₀ , то получим у ₀ =у 1 а + r ₀ , то

есть число у ₀ имеет такую же запись в системе счисления { а ; I } , как и число у ₀ в системе счисления { а ; I } . Следовательно, системы счисления { а ; I } и { а ; I } также эквивалентны.

Замечание. Очевидно, что если f – функция, переводящая систему счисления { а ; I } в { а‘ ; I 3 , то алгоритм сложения двух чисел f ( у ) и f ( в ) в системе счисления { а‘ ; I 3 легко получается из алгоритма сложения чисел у и в в системе счисления { а ; I } .

То же самое можно сказать и об инверсии знака.

Если функция f задаётся следующим равенством f ( y ) = Y , где Y — число, сопряжённое Y , то алгоритм умножения двух чисел у и в в системе счисления { а ; I } также легко получается из алгоритма умножения чисел y и в в системе счисления { а ; I } .

Квазиканонические системы счисления в S(i)

Кольцо S (i) целых элементов (целых гауссовых чисел) поля Q (i) состоит из элементов z = a + bi; a, b e Z.

При делении с остатком по норме на а , Norm ( а ) = 2, норма ненулевого остатка может равняться только единице. Таких остатков ровно четыре: { ± 1, ± i } , что в сочетании с вариантами выбора а : { ± 1 ± i } даёт 16 потенциальных комбинаций возможных оснований а и множества I , то есть 16 бинарных квазиканонических систем счисления. Однако, учитывая свойство 3, получаем, что в кольце S ( i )

достаточно исследовать лишь две системы счисления, а именно: { - 1 + i ; { 0, i } } и { 1 + i ; { 0, i } } .

Следующая теорема описывает все возможные ква-зиканонические системы счисления в кольце S ( i ) .

Теорема 1. В кольце целых алгебраических чисел

S (i) существуют ровно 8 бинарных квазиканониче- ских систем счисления, а именно: системы счисления с основаниями а = -1 ± i и множествами цифр {0,1}, {0, i}, {0, -1}, {0, - i} .

Доказательство. Заметим, что остатки от деления на число α, имеющие норму 1, можно представить в виде ik, где k = 1; 2; 3; 4, а основания систем счисления запишем как аn = (1 + i) • in-1, n = 1; 2; 3; 4 . Пока- жем, что справедлива следующая лемма.

Лемма 1. Пусть ае S ( i ) является основанием бинарной системы счисления, для которой множество цифр I выбирается из чисел r е S ( i ) , причём

||r || < ||а|| = 2. Тогда I = { 0, i^k } , где k = 1,2,3,4 .

Доказательство. Пусть r = r1 + r2 • i, а = а1 + а2i, в = a + bi . Подставляя выражения для в , а и r в формулу (1), имеем

Y =

а а 1 + b а ₂ - r ₁ а ₁ - r ₂ а ₂ 2

+

b а 1 - а а ₂ + г 1 а ₂ - r ₂ а ₁

i . (3)

r ₁ + r ₂ , следовательно, в качестве остатка выбираем r = i^k . Тогда Y однозначно определяется из формулы (1).                                                             ■

Таким образом, показано, что в системах счисления { а _n ; I = { 0, i^k } } возможно однозначное представление произвольного целого гауссова числа. Рассмотрим теперь конечность представления чисел в таких системах счисления, опираясь на свойство 2.

Лемма 2. В равенствах (2) найдётся такой элемент l , при котором Norm ( y l _{+ 1}) <  1.

Доказательство. Выясним, для каких систем остатков условие        Norm ( y _{m + 1} ) <  Norm ( Y _m )

V m = 0,1,..., l выполняется для каждого целого алгебраического числа Y _m .

Пусть Y m = a m ^{+ b}m i , r m = rm 1 ⁺ r m 2 i • Согласно формулам (2),

(Ym - rm )а (Ym - rm )а Norm (Ym - rm ) 2            2                2.

Подставляя последнее выражение в неравенство Norm (ym+1 )< am + bm, после преобразований получа- ем неравенство

( ^am ⁺ r m 1 ) ^{2 +} ( b m ⁺ r m 2 ) ² >  ² ( 4 ⁺ rrn 2 ) ,              ⁽⁴⁾

которое при r_m = 0 справедливо для всех Y _m * 0 .

Если r_m = i^k , то есть r m 1 + r m ₂ = 1, то неравенство ⁽⁴⁾ принимает вид ( ^am ⁺ r m 1 ) ^{2 +} ( b m ⁺ r m 2 ) 2 >  ². Оно верно для всех Y _m e Z ( i ), Norm ( Y _m ) ^ 2, r_m e { 0, i^k } , кроме Y m = ( ± 1 - 2 i ) • i k ^{- 1}     , Y m =^{- 2} i • i^{k - 1}     ,

Ym =(±1 - i )• ik-1.

Рассмотрим теперь системы счисления { - 1 + i ; { 0, i } } и { 1 + i ; { 0, i } } . В этих системах счисления неравенство (4) выполняется для всех Y _m , кроме Y m = ± 1 ^{- 2} i , Y m = ^{- 2} i , Y m = ± 1 ^- i , Y m = ^- i , Y m = ± 1. Представления для этих чисел получим, применив к ним формулы (2).

Так, в системе счисления { - 1 + i ; { 0, i } } :

для Y m = ^{1 - 2} i Y m + 1 =^{- 2 +} i , Y m + 2 = ^{1 +} i , Y m + 3 =^- i ,

Norm ( y m + 3 ) = 1;

для Y m = ^{- 1 - 2} i Y m + 1 = ^{- 1 + 2} i , Y m + 2 = ¹ ,

Norm ( y m + 2 ) = 1;

для Y m = ^{- 2} i Y m + 1 = ^{- 1 +} i , Y m + 2 = ¹ ,

Norm ( y m + 2 ) = 1;

для Y m = ^{1 -} i Y m + 1 = ^{- 1,} Norm ( Y m + 1 ) = 1;

для Y m = ^{- 1 -} i Y m + 1 = i , Norm ( Y m + 1 ) = 1.

В системе счисления { 1 + i ; { 0, i } } :

для ^Y m = ¹ - ² i ^Y m + 1 = ^{- 1} - ² i , ^Y m + 2 = ² - i , ^Y m + 3 = ² , Y m + 4 = । ⁺ i , Y m + 5 = i , Norm ( Y m + 5 ) = 1;

для ^Y m =^{- 1 - 2} i ^Y m + 1 =^{- 2 -} i , ^Y m + 2 = - ² , ^Y m + 3 = ^{- 1 +} i , Y m + 4 = i , Norm ( Y m + 4 ) = 1;

Для Y m =^{- 2} i Y m + 1 =^{- 1} — i , Y m + 2 = ^{- 1,} Norm ( Y m + 2 ) = 1;

Для Y m = ^{1 -} i Y m + 1 = ^- i , Norm ( Y m + 1 ) = 1;

Для Y m = ^{- 1} — i Y m + 1 = ^{- 1,} Norm ( Y m + 1 ) = 1.

Таким образом, доказано, что норма частного всегда меньше нормы делимого, за исключением конечного числа случаев, и, следовательно, через конечное число шагов она станет меньше либо равна 1. Во всех исключительных случаях показано, что через конечное число шагов норма частного также станет меньше либо равна 1. ■

Итак, найдётся такое значение l = q , при котором Norm ( y q _{+ 1}) = 0, следовательно, Y q _{+ 1} = 0, либо Norm ( y q _{+ 1}) = 1, то есть Y q _{+ 1} = ± 1; ± i • Для всех этих значений y q _{+ 1} легко проверить, что через конечное число шагов появится частное Y p = 0 в системе счисления { - 1 + i ; { 0, i } } . Поэтому из равенств (2) вытекает однозначное разложение числа y ₀ по степеням числа а = i - 1:

• -    для Y q + 1 = ⁰

Y 0 = r q а ^q + r q - 1 а ^{q - 1} + ... + r 1 а + r ,;

• -    для Y _{q + 1} = i

• Y ₀ = i -а ^{q + 1} + r_q a ^q + r_q - 1 а ^{q - 1} + ... + r ₁ а + r ₀;

• -    для Y _{q + 1} = - 1

Y ₀ = i -а ^{q + 2} + i -а ^{q + 1} + r q а ^q + r q - 1 а ^{q - 1} + ... + r ₁ a + r ₀;

• -    для Y _{q + 1} = - i

• Y ₀ = i а ^{q + 5} + i а ^{q + 4} + i а ^{q + 3} + 0 а ^{q + 2} + i а ^{q + 1} + r q а ^q + ... + r ₀; -для Y _{q + 1} = 1

Y 0 = i -аq+3 + i -аq+2 + i -аq+1 + rq аq +... + r0, где rt e {0; i}; t = 0;1;...;q.

Если рассмотреть систему счисления { 1 + i ; { 0, i } } , то при последовательном применении алгоритма деления с остатком возможно зацикливание: ^- для Y q + 1 = ^{- 1}

Y о =- 1 -а ^{q + 2} + i -а ^{q + 1} + r q а ^q + ... + r ₀;

где r t e { 0, i } ; t = 0;1;...; q .

Таким образом, в системе { 1 + i ; { 0, i } } и всех эквивалентных ей системах не любое целое гауссово число допускает конечное представление. ■

Из доказанного легко получается алгоритм записи целого гауссова числа y0 = a0 + b0i; a0, b0 e Z в систе ме счисления с основанием а = ±i -1 и алфавитом

I_k = { 0, i^k } .

Алгоритм 1.

Шаг 1. Полагаем p = 0 .

Шаг 2. Если для y _p = a_p + b_pi , сумма a_p + b_p чётная, то r_p = 0 .

Если a_p + b_p нечётная, то r_p = i^k .

Шаг 3. Вычисляем    y _{p + 1}   по формуле

v    _ (Yp -rp)а

• ^{Y p + 1}          2       .

Если Y _{p + 1} = 0 , то алгоритм закончен.

Если y _p + i ^ 0, то p = p + 1 и переходим к шагу 2.

■

Сходимость данного алгоритма следует из доказательства теоремы 1.

Рассмотрим теперь арифметические операции в системах счисления, указанных в теореме. Согласно свойству 3 и доказанной теореме, достаточно рассмотреть сложение лишь для одной системы счисления, например { - 1 + i ; { 0,1 } } . Алгоритм сложения чисел в такой системе счисления рассмотрен в работе [27].

Умножение. Реализация операции умножения даже в некоторых эквивалентных системах счисления отличается. В силу особенностей алфавита (одна из цифр является нулём), таблицы умножения для таких систем счисления сильно упрощаются, и достаточно записать разложение лишь одного числа для каждой системы счисления. Согласно свойству 3, алгоритм умножения чисел в системе счисления {а; I} легко получается из алгоритма умножения чисел в системе счисления {а; I} , поэтому достаточно рассмотреть лишь 4 системы из 8.

Для { i - 1; { 0, i } } i ² =- 1 = i а + i ;

для { i - 1; { 0, - 1 } }

(-1)2 = 1 = (-1)а4 +(-1)а3 +(-1)а2 +(-1);

для { i - 1; { 0, - i } }

(-i) = -1 = (-i)а2 +(-i)а + (-i);

для { i - 1; { 0,1 } } 1² = 1.

Поскольку алфавит системы счисления {а;{0,ik}} состоит из цифр 0 и ik , то умножение чисел a и c в этой системе счисления сводится к сложению m чисел, где m – количество цифр единичной нормы в записи числа c . Складываемые числа получаются из числа a следующим образом. При умножении числа на цифру ik, стоящую в разряде, соответствующем аp, к записи числа a справа добавляется p нулей. Числа, полученные при умножении на цифры единичной нормы неко- торых разрядов, складываются последовательно по два числа в соответствии с алгоритмом сложения.

Инверсия знака. Следует отметить, что инверсия знака будет одинаковой в различных системах счисления. Поэтому достаточно рассмотреть алгоритм лишь для одной системы счисления.

Пусть представление исходного числа в в систе-

N ме счисления {-1 + i;{0,i}} имеет вид в = ^акak .

к = 0

Тогда, учитывая формулу - i = i a ⁴ + i a ³ + i a ² + i , получаем следующий алгоритм инверсии знака.

Алгоритм 2.

Шаг 1. Полагаем к = 0.

Шаг 2. Если - a k = 0 или - a k = i, то переходим к шагу 3.

Если - a k = - i, то в текущий разряд записываем i и прибавляем i к разрядам к + 2, к + 3 , к + 4 .

Если - а_к = 2 i, 3i, ..., то раскладываем его в данной системе счисления и добавляем его к текущему представлению, начиная с разряда k , то есть действуем, как в алгоритме сложения. Переходим к шагу 3.

Шаг 3. к = к + 1.

Если к больше длины исходного числа в и - а_к = - а_{к + 1} = - а_{к + 2} = - а_{к + 3} = 0, то алгоритм закончен.

Иначе переходим к шагу 2. ■

Сходимость данного алгоритма обусловлена сходимостью алгоритма сложения, а также алгоритма представления чисел в системе счисления с основанием a = ± i - 1 и алфавитом 1_к = { 0, i^k }

Квазиканонические системы счисления в S ( i41 )

Кольцо S (i41) целых элементов поля Q (i 41) состоит из элементов z = а + bi41; а, b е Z.

При делении с остатком по норме на a, Norm (a) = 2 , норма ненулевого остатка может равняться только единице. Таких остатков ровно два: {±1} , что в сочетании с вариантами выбора a : {±iV2} даёт 4 потенциальных комбинации возможных оснований a и множества I , то есть 4 бинарных квазиканонических системы счисления. Учитывая свойство 3, получаем, что в кольце S (i41) достаточно исследовать лишь одну систему счисления, а именно: {iV2;{0,-1}} .

Следующая теорема описывает все возможные ква-зиканонические системы счисления в кольце S ( i V2) .

Теорема 2. В кольце целых алгебраических чисел

S (i V2) существуют ровно 4 бинарных квазиканони-ческих системы счисления, а именно: системы счис- ления с основаниями a = ±i41 и множествами цифр {0,1}, {0, -1} .

Доказательство проводится по схеме доказательства теоремы 1.

Из доказательства теоремы 2 легко получается алгоритм записи целого алгебраического числа Y0 = а0 + b0i41; а0, b0 е Z в системе счисления с осно ванием a = ±i41 и алфавитом In = {0, (-1)n} .

Алгоритм 3.

Шаг 1. Полагаем р = 0 .

Шаг 2. Если для у _р = а_р + b_pi41 а_р - чётное, то ^гр = 0.

Если а_р - нечётное, то r_p = ( - 1 ) ^к .

Шаг 3. Вычисляем   у р +1   по формуле v (y r )a y р+1          2       .

Если y _{р + 1} = 0, то алгоритм закончен.

Если y _{р + 1} ^ 0, то р = р + 1 и переходим к шагу 2. ■

Рассмотрим теперь арифметические операции в системах счисления, указанных в теореме. Согласно свойству 3 и доказанной теореме, достаточно рассмотреть сложение лишь для одной системы счисления, например, { i V1; { 0, - 1 } } .

Сложение. При сложении двух чисел в системе счисления { i V2; { 0, - 1 } } , иначе говоря, двух многочленов, получаем новый многочлен с коэффициентами 0,   -1 или -2. При этом, поскольку

- 2 = ( - 1 ) a ⁴ + ( - 1 ) a ², слагаемое вида - 2 a t преобразуется по формуле

-2a t = ((-1) a4 + (-1) a2 ) a t = (-1) at+4 + (-1) at+2.

В некоторых случаях преобразование суммы двух чисел с использованием последней формулы приводит к многочлену бесконечно большой степени с повторяющимся блоком коэффициентов (зацикливанию).

Очевидно, что любой многочлен от a , корнем которого является a = i41 , также будет обращаться в нуль.

Таким образом, любой «нулевой» многочлен должен делиться на выражение

(a - i 41) (a + i 41) = a2 + 2.

Из сказанного выше следует алгоритм сложения двух чисел, записанных в системы счисления с основанием i 2 .

Алгоритм 4.

Шаг 1. Складываем по разрядам два данных числа. При этом в записи суммы может присутствовать цифра - 2 , не входящая в алфавит системы счисления. Тогда переходим к шагу 2. Если таковой цифры не встретилось, то получаем искомую сумму.

Шаг 2. Используем формулу из таблицы сложения для каждой - 2 в записи числа (по одному разу для каждого разряда), при этом в записи может появиться и цифра - 3. После этого, двигаясь от нулевого разряда, находим первую цифру справа, большую единицы. Эта цифра и все другие, стоящие слева от неё, определяют некоторый многочлен P ( x ) . Если P ( x ) делится на ( - 1 ) x ² + ( - 2 ) без остатка, то считаем его «нулевым», если с остатком, то повторяем шаг 2, учитывая, что

-3 = (-1)а4 + (-1)а2 + (-1) = (-1)0(-1)0(-1)а .

Если в сумме не осталось цифр, не принадлежащих алфавиту { 0, - 1 } , то получаем искомый результат. ■

Умножение. Согласно свойству 3, алгоритм умножения чисел в системе счисления {а; I} легко по- лучается из алгоритма умножения чисел в системе счисления {а; I} , поэтому достаточно рассмотреть лишь 2 системы из 4.

Для {iV2;{0,-1}} (-1) =1 = (-1)а2 +(-1);

для { i V2; { 0,1 } } ( 1 ) 2 = 1.

Поскольку   «алфавит»   системы счисления

{а;{0,(-1)k}} состоит из цифр 0 и (-1)k, то умноже- ние чисел a и c в этой системе счисления сводится к сложению m чисел, где m – количество цифр единичной нормы в записи числа c . Складываемые числа получаются из числа a следующим образом. При умножении числа на цифру (-1)k, стоящую в разря де, соответствующем ар , к записи числа а справа добавляется p нулей. Числа, полученные при умножении на цифры единичной нормы некоторых разрядов, складываются последовательно по два числа в соответствии с алгоритмом сложения.

Инверсия знака. Следует отметить, что инверсия знака будет одинаковой в различных системах счисления. Поэтому достаточно рассмотреть алгоритм лишь для одной системы счисления.

Пусть представление исходного числа в в систе-

N ме счисления {iV2;{0,-1}} имеет вид в = ^akаk, то к=0

N есть -0 = ^ (-ak )аk . Тогда, учитывая формулу к=0

1 = (-1)а2 +(-1), получаем следующий алгоритм ин версии знака.

Алгоритм 5.

Шаг 1. Полагаем к = 0.

Шаг 2. Если -ак = 0 или -ак = -1 , то переход к шагу 3.

Если -ак = 1 , то в текущий разряд записываем -1 и прибавляем -1 к разряду к + 2 . Переходим к шагу 3.

Шаг 3. к = к + 1.

Если к больше длины исходного числа в, то ал- горитм закончен.

Иначе переходим к шагу 2. ■

Сходимость всех алгоритмов для кольца

S ( i V2)

обосновывается аналогично сходимости алгоритмов для кольца S ( i ) .

Квазиканонические системы счисления в s (i V7)

Кольцо S ( i 4l ) целых элементов поля Q ( i  )

состоит из элементов

a + bi V?          , x

z =--- 2--- ; a = b ( mod2 ) , a , b e Z .

При делении с остатком по норме на а,

Norm (а) = 2, норма ненулевого остатка может рав- няться только единице. Таких остатков ровно два:

{ ± 1 } , что в сочетании с вариантами выбора а :

; { 0, - 1 } и 2; { 0, - 1 } .

ния с основаниями

а =---2-- и множествами цифр

проводится по схеме доказатель-

и алфавитом I n = { 0; ( - 1 ) ^к } .

р = 0.

Y р

^а 1 ^ар

-а ₂ b_p = 0 ( mod4 ) ,

то r p = 0 .

Если а 1 a p -а ₂ b p = 2 ( mod4 ) , то r p = ( - 1 ) k .

Переходим к шагу 3.

Шаг 3. Вычисляем    у p _{+ 1}   по формуле

v =(Yр -гр )а

^Y p ^{+ 1}          2       .

Если у _{p + 1} = 0, то алгоритм закончен.

Если у _{p + 1} ^ 0, то p = p + 1 и переходим к шагу 2. ■

Рассмотрим теперь арифметические операции в таких системах счисления. Согласно свойству 3 и доказанной теореме, достаточно рассмотреть сложение лишь для двух систем счисления, например:

( i ? ;_{о,-1}| и        '7 ;{0,-1}-.

[     2      1      ;]     [ 2     1      ;

Сложение. При сложении двух чисел в системе

Шаг 1. Складываем по разрядам два данных числа. При этом в записи суммы может присутствовать цифра - 2, не входящая в алфавит систем счисления. Тогда переходим к шагу 2. Если таковой цифры не встретилось, то получаем искомую сумму.

Шаг 2. Используем формулу из таблицы сложения для каждой - 2 в записи числа (по одному разу для каждого разряда), при этом в записи может появиться и цифра - 3. После этого, двигаясь от нулевого разряда, находим первую цифру справа, большую единицы. Эта цифра и все другие, стоящие слева от неё, определяют некоторый многочлен P ( x ). Если P ( x ) делится без остатка на ( - 1 ) x ² + ( - 1 ) x + ( - 2 ) для системы счисления l- 1 + i41                       . ₂        , х

<---------;{0,-1}^ или на (-1) x2 + x + (-2) для систе- мы счисления

1 + i У?

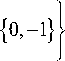
, то считаем его «нуле-

счисления

- 1 + i У?

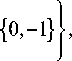
иначе говоря, двух

многочленов, получаем новый многочлен с коэффициентами 0, -1 или -2. При этом, поскольку - 2 = ( - 1 ) а ³ + ( - 1 ) а , то слагаемое вида - 2 а ‘ преобразуется по формуле

вым». Если с остатком, то повторяем шаг 2.

Если в сумме не осталось цифр, не принадлежащих алфавиту { 0, - 1 } , то получаем искомый результат. ■

Умножение. Согласно свойству 3, алгоритм умножения чисел в системе счисления { а , I } легко по-

-2а t = ((-1)а3 + (-1) а) а t = (-1) а t+3 + (-1) а t+1.

Замечание. В некоторых случаях преобразование суммы двух чисел с использованием последней фор-

мулы приводит к тому, что алгоритм не сходится за конечное число шагов. Но данный недостаток можно

лучается из алгоритма умножения чисел в системе счисления { а , I } , поэтому достаточно рассмотреть лишь 4 системы из 8.

Для |- 1^7 ; { 0, - 1 }

компенсировать следующим образом.

Очевидно, что любой многочлен от а , корнем ко

(-1)2 = 1 = (-1)а2 + (-1)а + (-1);

торого является а =

- 1 + i 4l 2

также будет обращать-

ся в нуль.

Таким образом, любой «нулевой» многочлен должен делиться на выражение

а

- 1 + i 41 Y - 1 - i 4l ------ а--

2 Л 2

= а2 + а + 2.

для

для

-1 + i У?

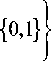
( 1 ) 2 = 1;

1 + i У7

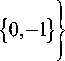
( -1) = 1 = ( -1) а3 + ( -1) а + ( -1) ;

для

1 + i У?

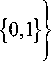
( 1 ) 2 = 1.

При сложении двух чисел в системе счисления

1+ iт al        . . - . . . .

------;{0, - 1} ^ получаем новый многочлен с коэф-

Поскольку алфавит системы счисления

{а;{0, (-1)k}} состоит из цифр 0 и (-1)k, то умноже- фициентами 0, -1 или -2. В этом случае любой «нулевой» многочлен должен делиться на выражение

1+ i У? У 1 - i У7      2     .

а--II а--I = а - а + 2.

2 Л 2 )

Из сказанного выше следует алгоритм сложения двух чисел, записанных в системе счисления с осно-±1 + i У?

ванием         .

Алгоритм 7.

ние чисел a и c в этой системе счисления сводится к сложению m чисел, где m – количество цифр единичной нормы в записи числа c . Складываемые числа получаются из числа a следующим образом. При умножении числа на цифру ( - 1 ) k , стоящую в разряде, соответствующем а ^p , к записи числа а справа добавляется p нулей. Числа, полученные при умножении на цифры единичной нормы некоторых разрядов, складываются последовательно по два числа в соответствии с алгоритмом сложения.

Инверсия знака . Следует отметить, что инверсия знака будет одинаковой в различных системах счисления. Поэтому достаточно рассмотреть алгоритм лишь для одной системы счисления.

Пусть представление исходного числа в в систе-

N ме счисления {а;{0,-1}} имеет вид в = Е akа k , то к=0

N есть -0 = Е (-ak )ак . Тогда, учитывая формулу k=0

1 = (-1)а2 + (-1), получаем следующий алгоритм ин- версии знака.

Алгоритм 8.

Шаг 1. Полагаем k =0.

Шаг 2. Если - a k = 0 или - a k = - 1, то переход к шагу 3.

Если - a k = 1, то в текущий разряд записываем - 1 и прибавляем –1 к разрядам k +1 и k +2 для системы

[^- 1 + i ^ _г ]

счисления <-------;{0,-Щ (прибавляем -1 к раз рядам к +1 и к + 3 для системы счисления |1+2^ ;{0,-1}j).

Если – a k = –2,–3,…, то раскладываем его в данной системе счисления и добавляем его к текущему представлению, начиная с разряда k , то есть действуем, как в алгоритме сложения. Переходим к шагу 3.

Шаг 3. k = k +1.

Если к больше длины исходного числа в и a_{k + 1} = 0, a_{k + 2} = 0 , то алгоритм закончен.

Иначе переходим к шагу 2. ■

Сходимость всех алгоритмов для кольца

S ( i Л )

обосновывается аналогично сходимости алгоритмов для кольца S ( i ) .

Заключение

В работе подробно рассмотрены алгоритмы представления целых элементов (в том числе и обычных целых чисел) и реализации основных арифметических операций в кольцах целых алгебраических чисел мнимых квадратичных полей.

В отличие от метода работы [26], для представления чисел в системах счисления с основаниями в виде целого алгебраического числа используется факт наличия в кольцах целых алгебраических чисел квадратичных полей алгоритма деления с остатком по норме.

Предложенный подход достаточно легко обобщается на случай других квадратичных расширений, для элементов которых есть алгоритмы деления с остатком по норме и на случай небинарных систем счисления.

Рассмотренный подход обеспечивает дополнительную криптостойкость системы кодирования по методу работы [28] или новые алгоритмы параллельного вычисления произведения больших целых чисел методом, описанным в монографии [25].

Работа выполнена при финансовой поддержке РФФИ (гранты 09-01-0511а, 12-01-00822а, 12-0131316 мол a).