Классификация объектов с помощью однопиксельной визуализации и нейронных сетей

Традиционные методы формирования изображений используют матричные детекторы, обеспечивающие пространственное разрешение целевого объекта. Однако использование матричных детекторов вне спектрального диапазона чувствительности кремния сталкивается с серьезными технологическими трудностями. Альтернативой матричным детекторам является использование детектора без пространственного разрешения в сочетании с пространственной модуляцией освещения объекта и вычислительными алгоритмами восстановления изображения – метод, получивший название однопиксельная визуализация [1, 2]. Одно из важных преимуществ однопиксельной визуализации состоит в возможности гораздо более широкого выбора одного детектора по сравнению с матрицей детекторов. Например, так можно получать изображения с помощью однофотонного детектора в ближней инфракрасной области [3] или использовать фоторезистор с широким спектральным диапазоном [4].

Процесс сбора данных в однопиксельной визуализации состоит в освещении объекта последовательностью пространственно-неоднородных световых паттернов и измерения соответствующего им интегрального количества света, отраженного от объекта, характеризующего соответствие паттерна объекту (сэмплирование объекта последовательностью паттернов). Вычислительная задача однопиксельной визуализации заключается в восстановлении изображения по известному набору паттернов и измеренным данным. В последние годы методы машинного обучения

продемонстрировали большой потенциал в решении этой задачи [5– 10].

В практических применениях задача восстановления изображения, то есть получения пространственного распределения интенсивности света от объекта, может быть лишь промежуточным шагом. Типичным примером является классификация объектов [8]. В стандартном подходе эта задача решается в два шага: на первом шаге мы получаем изображение объекта, а на втором шаге вычисляется функция от этого изображения, по результату которой объект относится к одной из нескольких групп. Применение однопиксельной визуализации может решить задачу классификации объектов без промежуточного шага в виде восстановления изображения.

В данной работе мы демонстрируем классификацию изображений методом однопиксельной визуализации с помощью сверточных нейронных сетей (СНС). Наша основная идея применимости СНС в однопиксельной визуализации в данном случае состоит в том, что на первом шаге стандартного подхода к классификации объектов мы получаем сильно избыточную информацию об объекте (изображение объекта), которую далее сводим к гораздо меньшей (классу объекта). Поэтому мы можем изначально сэмплировать объект не с целью промежуточного получения изображения, а напрямую классифицировать набор сэмплов. Из такой постановки задачи появляется возможность сократить количество сэмплов и уменьшить время экспонирования объекта. Мы анализируем возможности такого ускорения, и находим оптимальные параметры всей схемы однопиксельной визуализации для решения задачи классификации объектов на примере набора рукописных цифр MNIST.

Статья организована следующим образом: в параграфе 1 приводятся основные сведения о методе однопиксельной визуализации, в параграфе 2 обсуждается архитектура сверточной нейронной сети в контексте применения для однопиксельной классифика-ци, в параграфе 3 показаны результаты классификации изображений, в параграфе 4 анализируется влияние шума детектора на точность классификации.

1.    Однопиксельная визуализация

Устройство для однопиксельной визуализации (однопиксельная камера) включает в себя два основных компонента. Первый компонент – это пространственный модулятор света, позволяющий создать неоднородное структурированное освещение объекта (спроецировать на объект серию световых паттернов), или же структурировать сфокусированное на пространственном модуляторе света изображение объекта (пропустить изображение объекта через серию паттернов). Пространственный модулятор света может быть реализован по-разному, например, это может быть цифровой микрозеркальный модулятор, состоящий из массива маленьких управляемых зеркал, каждое из которых может принимать два положения с разными углами отклонения («включено» и «выключено»). Это позволяет произвольно маскировать свет, освещающий объект или отражённый от объекта.

Далее структурированный свет от объекта посредством собирающей линзы фокусируется на втором компоненте однопиксельной камеры – однопиксельном детекторе света (например, фотодиоде), который позволяет измерить общую интенсивность света для каждого светового паттерна. Визуализируемый объект последовательно освещается с использованием M различных световых паттернов, что позволяет измерить M значений интенсивности света. Далее для получения изображения требуется обработать набор из паттернов и соответсвующих им интенсивностей.

Рассмотрим математическую модель процесса однопиксельной визуализации. Пусть изображение визуализируемого объекта имеет W (width) и H (height) пикселей по ширине и высоте соответственно, но далее мы будем использовать только общее число пикселей N = W × H (такой же будет и размерность световых паттернов). Тогда, если в процессе работы камеры мы использовали M паттернов, на выходе мы имеем вектор S =( s 1 ,…, s M ) интенсивностей для каждого паттерна. Если представить набор из M матриц световых паттернов в векторизованном виде P = ( P 1,..., P M ) ^T , где P i =( p i,..., p WH ) — векторизованная матрица i- го паттерна , то для векторизованно го изображения объекта I =(i 1 ,…, i WH ) взаимосвязь полученных отсчётов интенсивностей и пикселей изображения имеет вид

S= PI. (1)

Если бы мы в результате работы камеры получили M = N значений интенсивностей без каких - либо от клонений от такого модельного описания ( без шума аппаратуры и с неограниченным временем набора статистики фотоотсчётов ), то искомое изображение можно было бы получить , выполнив умножение на обратную матрицу паттернов I = P ^–1S. Далее это изображение можно классифицировать стандартными методами классификации , например , с использовани ем СНС . Однако на практике такой подход не опти мален по нескольким причинам . Во - первых , измерен ные величины интенсивности содержат шум , поэтому восстановленное таким образом изображение также содержит шум , что ограничивает точность классифи кации даже для полного набора измерений . Во - вторых , любой алгоритм восстановления сам по себе также допускает некоторую неточность и вносит ис кажения в изображение , особенно сильные при малом количестве сэмплов , что затрудняет дальнейшую классификацию . Поэтому возможность избежать ша га , связанного с восстановлением изображения , мо жет существенно упростить задачу классификации без необходимости совместной оптимизации проме жуточного восстановления искаженного изображения и последующей классификации .

Как мы покажем ниже , задачу классификации можно эффективно решить при M << N, то есть при существенно неполном наборе измерений , за счет ис пользования СНС для обработки результатов измере ний интенсивности света . В нашей модели СНС - классификатора мы используем промежуточное пред ставление размером 28 на 28, которое не соответству ет изначальному изображению ( т . е . отсутствует вос становление изображения ), но удобно для обучения модели классификации .

2.    Cверточные нейронные сети для однопиксельной классификации

Для классификации объектов по сигналам с одно пиксельной камеры в начале были выбраны изобра жения и паттерны размером N = 28×28 = 784. Изобра жения были взяты из стандартного набора данных MNIST – набор данных образцов рукописного напи сания цифр .

Мы разработали и обучили сверточную нейронную сеть ( СНС ) на входных данных S и выходных данных разметки набора MNIST. Структурно СНС состоит из нескольких блоков , схематично представ ленных на рис . 1: входного полносвязного (decode_lin) ( блоки fc1, fc2), обратных сверточных блоков (decode_conv) ( блоки (deconv1), (deconv2), (deconv3), (deconv4)), сверточных блоков (conv1), (conv2), (conv3) и выходного полносвязного (fc). Сна чала полносвязные слои преобразуют данные сигна лов размера M в данные размера 288. Далее сверточ ные блоки сворачивают данные до размерности 128.

Финальный полносвязный блок преобразует данные с последнего сверточного слоя в выходные данные размера 10. По номеру элемента выходных данных, имеющего максимальное значение, определяется цифра на изображении набора MNIST, с которого получены сигналы S , поданные на вход СНС. В Приложении приведён подробный список слоев СНС и использованных функций активации.

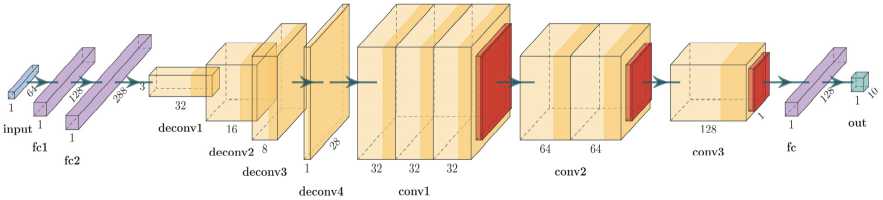
Рис. 1. Схематичное изображение архитектуры нейронной сети, использованной нами для классификации изображений

В начале для обучения были взяты наборы паттернов с числом паттернов 16, 32, 64 (соответственно, матрицы паттернов P имели размер 784×16, 784×32 и 784×64). Матрицы паттернов задавались как случайные бинарные матрицы со значениями 0 и 1, причем вероятность 0 варьировалась от 0,5 до 0,99. Отметим несколько особенностей использования паттернов со случайной структурой.

Во-первых, такие паттерны не обусловлены структурой и особенностями датасета (или класса примерных изображений, на которых далее будет работать однопиксельная камера), а также напрямую не связаны с алгоритмом обработки сигнала с однопиксельной камеры. В частности, вместо классификации рукописных цифр из набора MNIST могут быть использованы и другие алгоритмы, без внесения изменения в набор паттернов и экспериментальную реализацию однопиксельной камеры. Например, может быть выполнено восстановление изображения методами сжатого сэмплирования [1], или же проведена классификация изображения не по десяти классам, соответствующим рукописным цифрам, а по каким-либо другим особенностям изображения. То есть на одном и том же наборе сигналов с однопиксельного детектора могут быть выполнены разные алгоритмы его обработки, что делает такой подход достаточно универсальным. В других подходах, например в работе [8], используемый набор паттернов связан как с конкретным датасетом (MNIST), так и с конкретным алгоритмом обработки сигналов (классификатором). С одной стороны, это несколько улучшает точность классификации (96,1 % вместо 91,5 %). С другой стороны, это ограничивает однопиксельную камеру, запрограммированную на данный набор паттернов, одной конкретной задачей.

Во-вторых, случайные паттерны, в отличие от конкретно заданных паттернов, могут быть реализованы более широким классом экспериментальных методов. Для создания произвольных паттернов в большинстве экспериментальных работ по однопиксельной визуализации используются микрозеркальные пространственные модуляторы света. Это очень удобный инструмент, позволяющий создавать пат- терны с высоким разрешением вплоть до 4К и менять их на частоте порядка 10 килогерц. Тем не менее, полноценное управление таким устройством требует низкоуровневого программирования ПЛИС и технически трудоемко. Если же не требовать создания каких-либо конкретно заданных паттернов, то их можно реализовать другими методами. Например, можно использовать случайную спекл-структуру рассеянного когерентного света. Поэтому использование случайных паттернов может как упростить экспериментальную реализацию, так и повысить частоту смены паттернов.

Для всех запусков обучения было выбрано 30 эпох обучения с оптимизатором ADAM [11]. В оптимизаторе был выбран параметр скорость обучения lr=0,0003 первые 15 эпох и lr=0,0001 последние 15 эпох. В качестве валидационного набора были случайно отобраны 12000 изображений обучающего набора MNIST, обучение проводилось на оставшихся 48000 изображений. 10000 тестовых изображений использовалось из тестового набора MNIST. В качестве функции потерь, определяющей расходимость между ожидаемым и предсказанным значением, была выбрана отрицательная логарифмическая функция правдоподобия. Обучение проводилось на i5-8250U CPU.

3.    Результаты работы сверточной нейронной сети

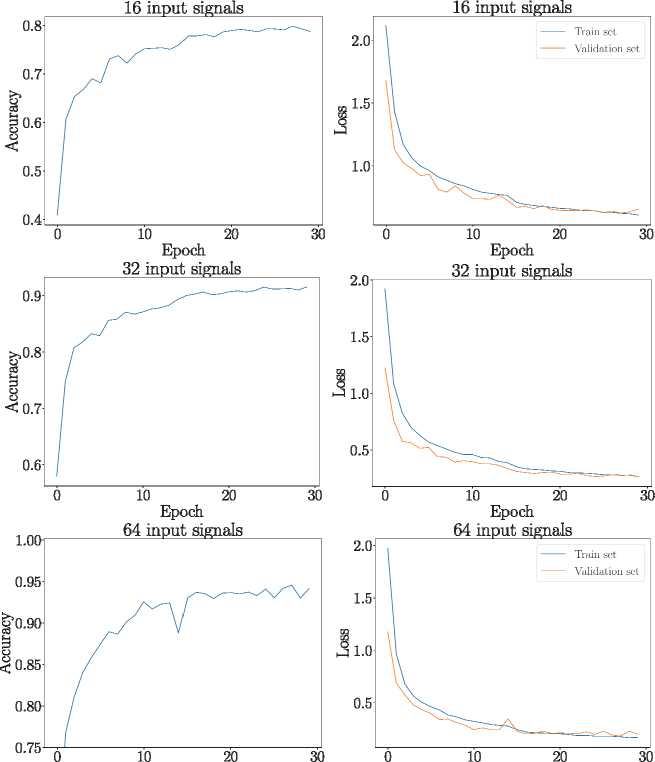
Результаты классификации объектов методом однопиксельной визуализации с помощью обученных СНС представлены на рис. 2. Наилучшая точность распознавания рукописных цифр 94,1 % была получена в конфигурации с 64 паттернами. Отметим, что 64 паттерна составляют менее 9% от полного набора паттернов для изображений 28 на 28. Также отметим, что даже использование всего 16 паттернов (чуть более 2 % от полного набора) показывает хороший результат (точность 78,7 %).

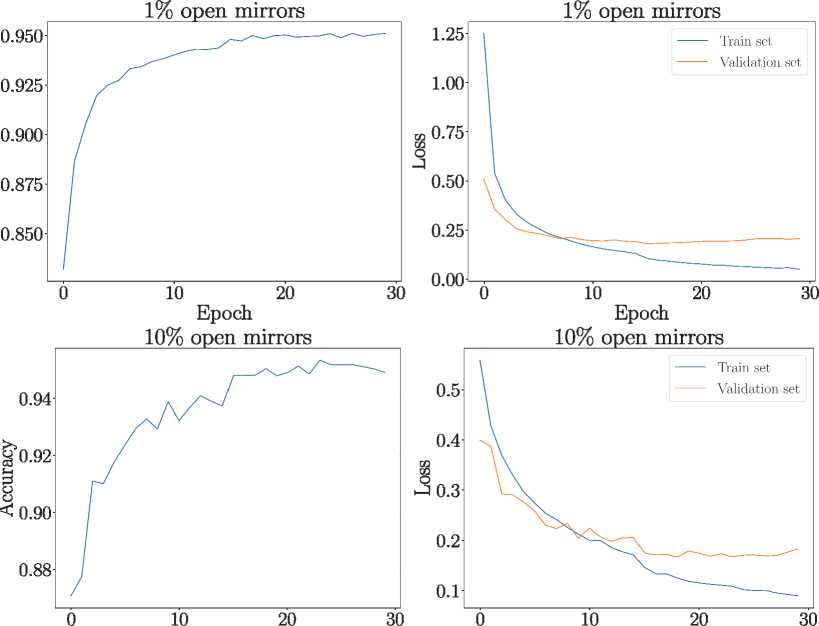
Далее рассмотрим вопрос об оптимизации соотношения нулей и единиц в используемых паттернах. При классификации изображений у нас может быть использована некоторая априорная информация о наборе возможных изображений. В частности, для набора MNIST распределение светлых и темных пикселей не равновероятно по всему изображению. Кроме того, сэмплирование изображений случайными паттернами с разными вероятностями нулей и единиц с последующим восстановлением изображения методами сжатого сэмплирования показывает, что оптимальный набор паттернов получается при очень небольшой вероятности единиц [12, 13]. В частности, для набора MNIST распределение светлых и темных пикселей не равновероятно по всему изображению. Поэтому нами была обучена СНС на матрицах паттернов с неравновзвешенными значениями 1 и 0. Для этого были случайно сгенерированы матрицы с 10% и 1% единиц (соответственно 90% и 99% нулей). Оптимизатор, количество эпох, скорость обучения, функция потерь, набор данных не менялись.

Epoch                                 Epoch

Рис. 2. Точность (Accuracy) обучения по тестовому набору и динамика функции потерь (Loss) в ходе обучения. Количество паттернов и входных сигналов на СНС – 16 (первая строка), 32 (вторая строка) и 64 (третья строка). Точность классификации, достигнутая к концу обучения, – 78,7 %, 91,5 % и 94,1 % соответственно

Был выбран набор из 64 паттернов, т.к. при таком количестве была достигнута наилучшая точность распознавания символов в предыдущем пункте. Результаты классификации представлены на рис. 3.

Характерно, что СНС за 30 эпох существенно переобучается (функция потерь на тестовом наборе дает значения существенно выше, чем на тренировочном наборе), к началу переобучения (8–9 эпоха). В обоих случаях достигается точность около 93 %, что слабо отличается от результатов для равновзвешенной матрицы 64 паттернов.

Для обученной модели можно было бы ожидать, что в промежуточных слоях, а именно после блока

(decode_conv) в промежуточных значениях размера 28 на 28, могло быть достигнуто полное восстановление изображения (что могло бы быть интересным результатом, позволяющим не находить под веса обученной нейросети специально подобранные паттерны, а ограничиться случайными). Тем не менее восстановления изображения в промежуточных слоях не достигается, как показано на рис. 4.

4.    Шум детектора в однопиксельной классификации

Как мы отмечали ранее, в реальном эксперименте сигнал однопиксельного детектора всегда содержит шумовую составляющую. Для апробации результатов нашей работы на практике целесообразно проанализировать влияние шума на точность классификации.

Для этого рассмотрим шум как случайные флуктуации сигнала в виде:

S' = P • I * N [ц,о],                                  (2)

где * - поточечное умножение, а N [ц, о] - матрица случайных величин размера M×N, где каждый эле- мент – случайная величина с гауссовым распределением со средним ц = 1 и среднеквадратичным о = 0,01, 0,03, 0,06 и 0,1.

На таких зашумленных сигналах с выбранными 64 паттернами были получены обученные веса СНС. Оптимизатор, количество эпох, скорость обучения, функция потерь, набор данных были оставлены теми же, что и в предыдущем процессе обучения.

Epoch                                Epoch

Рис. 3. Точность (Accuracy) обучения по тестовому набору и динамика функции потерь (Loss) в ходе обучения. Количество паттернов и входных сигналов на СНС – 64. Соотношение 1 и 0 в матрице паттернов – 1 / 99 (верхний ряд) и 1 / 9 (нижний ряд). Точность к моменту переобучения, – 93,1 % и 93,2 % соответственно

BIBB

Original images

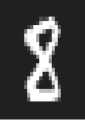
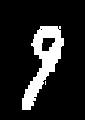
Рис. 4. Сравнение исходных изображений и промежуточных изображений после блока (decode_conv)

Intermediate output

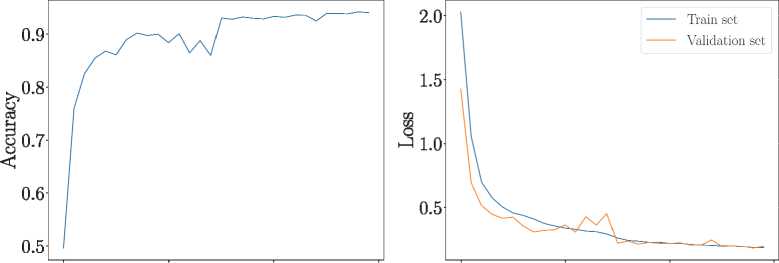
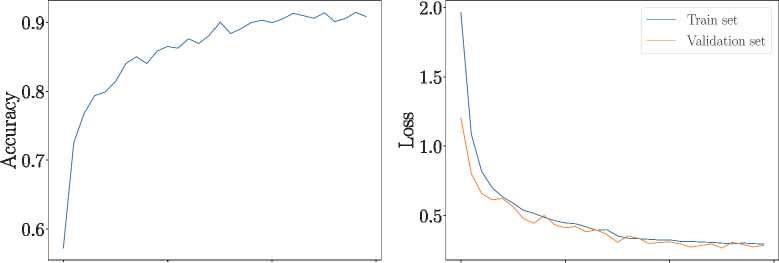
Результаты представлены на рис. 5. При небольшом шуме о = 1 % результаты аналогичны тем, что получены в отсутствие шума – 94 %. Приемлемые результаты наблюдаются при средней вели- чине шума о = 3 %, где точность распознавания символов достигает почти 91 %. Большой шум о =10% дает значительно худшие результаты, точность падает до менее 70 %.

1% noise                               1% noise

0          10          20          30        0          10          20          30

Epoch                                Epoch

3% noise                               3% noise

0           10          20          30         0           10          20          30

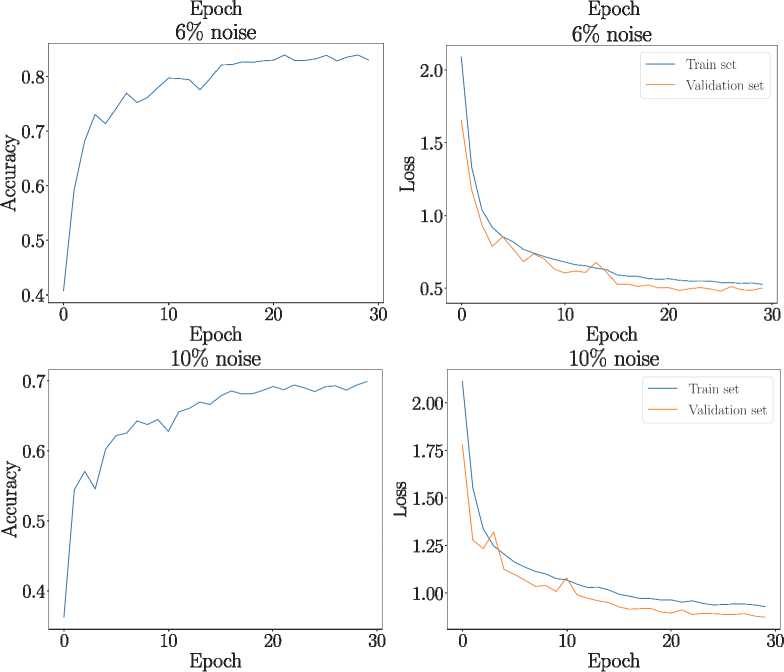
Рис. 5. Точность (Accuracy) обучения по тестовому набору и динамика функции потерь (Loss) ходе обучения. Количество паттернов и входных сигналов на СНС - 64. Уровень шума а = 1 %, 3 %, 6 %, 10 % (первый, второй, третий и четвертый ряд). Точность к концу обучения – 94 %, 90,8 %, 83 % и 69,9 % соответственно

Заключение

В данной работе мы продемонстрировали возможность распознавания и классификации объектов с помощью метода однопиксельной визуализации с применением сверточных нейронных сетей. На наборе изображений рукописных цифр MNIST мы показали, что можно использовать существенно неполные измерения объекта и при этом получать достаточно высокую точность классификации. Так, с использованием всего лишь 32 паттернов (примерно 4% от полного набора) можно достичь точность классификации выше 90%. Также мы продемонстрировали, что реалистичный шум детектора в виде случайных гауссовских флуктуаций в несколько процентов от величины сигнала несущественно влияет на точность классификации. Таким образом, применение нейронных сетей для задач, связанных с распознаванием объектов, в контексте однопиксельной визуализации является крайне перспективным направлением как с точки зрения существенного сокращения количества необходимых измерений и времени обработки сигнала, так и с точки зрения устойчивости к шумам детектирования. В качестве продолжения данного исследования стоит обратить внимание на сравнение данного метода с современными классификаторами [14], совмещенными с методами полного однопиксельного восстановления изображения, а также анализ для разных подходов точности классификации и особенностей практической реализации.

Исследование выполнено за счет гранта Российского научного фонда №    23-22-00381,