Классификация орбитальных объектов по спектральной информации

спутника. В астрономических исследованиях фотометрические временные ряды весвма часто используются для определения двойных и переменных звезд и экзопланет [1]. Более того, с помощью фотометрических характеристик ученым удалось определить форму и параметры вращения астероидов [2], [3].

Помимо кривых блеска большой вклад вносит измерение яркости объекта с помощью различных световых фильтров. Подобный подход позволяет анализировать не только временные, но и спектральные характеристики [4].

Каждый материал взаимодействует со светом согласно своему индивидуальному композитному составу. Спектры отражательной способности распространенных материалов космических аппаратов могут быть использованы для определения вещественного состава космического мусора. Классификация материалов космического мусора необходима для оценки риска столкновения, которому подвергаются действующие космические аппараты, и позволяет проследить происхождение обломков после столкновения. Более того, классификация материала может помочь в вычислении альбедо, что позволит определить размер удаленного объекта [5-7].

Отражательная спектроскопия широко использовалась для определения состава микрометеороидов и космического мусора, в частности при изучении астероидов в 1970-х. В 1990-х она стала применяться для исследования материалов космических аппаратов [8]. Спектральные измерения, полученные в лабораторных условиях, являются важной опорной информацией для анализа состава, позиции и движения объекта по орбите. Отражательная спектроскопия показала себя надежным инструментом для определения характеристик материалов, часто используемых в космической индустрии, таких как алюминий, нержавеющая сталь, стекло, золото, различные кремниевые краски и множество солнечных панелей. Спектральные измерения подобных материалов, полученные в лаборатории, могут быть использованы для сравнения с спектроскопическими или фотометрическими данными, полученными удаленно с помощью телескопов [7].

В данной работе изучается применение спектральной информации, полученной с помощью соответствующего оборудования, для решения обратной задачи спектрофотометрии, классификации космических объектов, таких как космический мусор и спутники. Получены спектральные характеристики материалов, широко используемых при конструировании космических аппаратов. Эти данные использованы для создания спектральной библиотеки. Проведен кластерный анализ с целью определения параметров световых фильтров для эффективной классификации материалов.

• 2.    Измерения спектров

Первой задачей, рассматриваемой в данной работе, является измерение и анализ спектров типичных для космических аппаратов материалов с целью эффективной классификации объектов наблюдения.

Для снятия спектральных характеристик был использован прибор ASD FieldSpec@ 3. Это спектрорадиометр общего назначения, используемый для измерения отражаемости, коэффициента пропускания и светимости. ASD FieldSpec@ 3 компактен, портативен и точен. Он позволяет измерять отраженный свет в диапазоне от видимого до ближнего инфракрасного света (350-2500 нм) за время 0.1 секунды на спектр. Спектрорадиометр имеет 512 каналов в видимом и ближнем инфракрасном диапазоне (VNIR) и более 1000 каналов в коротковолновом инфракрасном диапазоне (SWIR) [9]. Полученные с помощью прибора данные хранятся в компьютерной системе, где на их основе строится график отражающей способности.

В качестве одного из типичных для космических аппаратов материалов выбрана экранно-вакуумная теплоизоляция (ЭВТИ). ЭВТИ — это материал, покрывающий поверхности ракетных ступеней и спутников для термоизоляции. Обычно состоит из нескольких материалов, расположенных в виде множества слоев, внешняя часть которых покрыта тонким слоем алюминия, меди или золота. При отделении фрагмента ЭВТИ от спутника или космического корабля его орбита может сильно изменятся из-за высокого отношения площади к массе, так как подобный фрагмент подвержен сильному влиянию давления солнечного света.

Другим часто используемым материалом является алюминий из-за его низкой плотности. Прочность чистого алюминия не высока, поэтому он используется в сплаве с другими металлами, которые делают его намного прочнее. Алюминий используется для изготовления корпуса и несущих конструкций.

Главным источником энергии для космических аппаратов на орбите Земли являются солнечные панели, изготовленные из галия и кремния. Так как для генерации электричества требуются большие площади, освещенные потоком солнечного света, солнечные панели составляют значительный процент поверхности космического аппарата. Именно поэтому целесообразно выбрать солнечную панель как один из материалов для исследования.

Образцы, изготовленные из данных материалов, устанавливаются в подвижном креплении лабораторной установки, которое позволяет изменять относительное положение образца, источника света и приемного устройства, роль которого выполняет конец оптоволоконного кабеля. Каждый измеренный спектр характеризуется углом поворота образца вокруг его оси и положением источника света, в качестве которого используется светодиодный фонарь. Кроме того, спектры данных материалов были также получены при солнечном свете. На рисунках 1, 2 и 3 изображены подобные спектры.

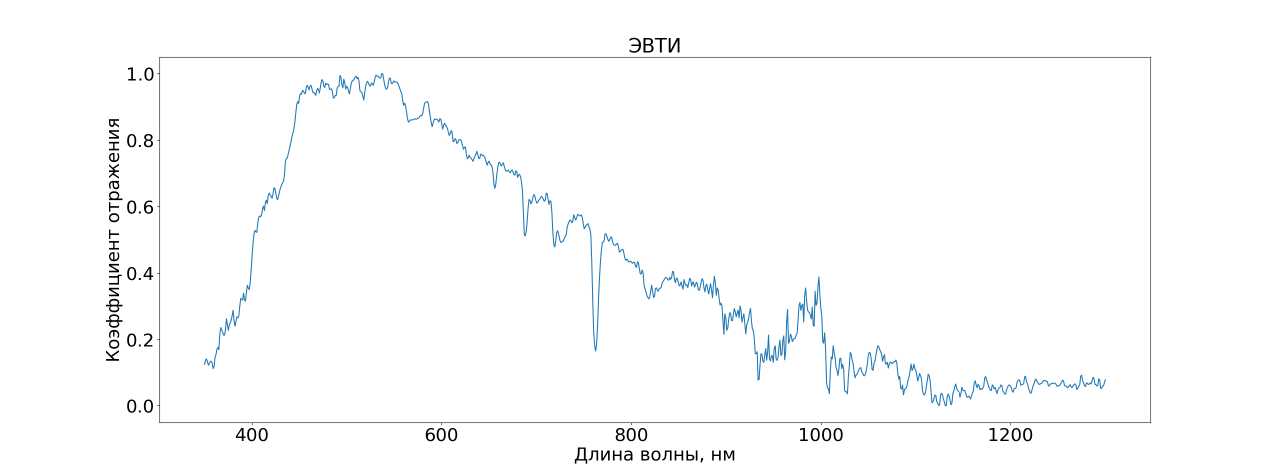
Рис. 1. Спектр ЭФТИ

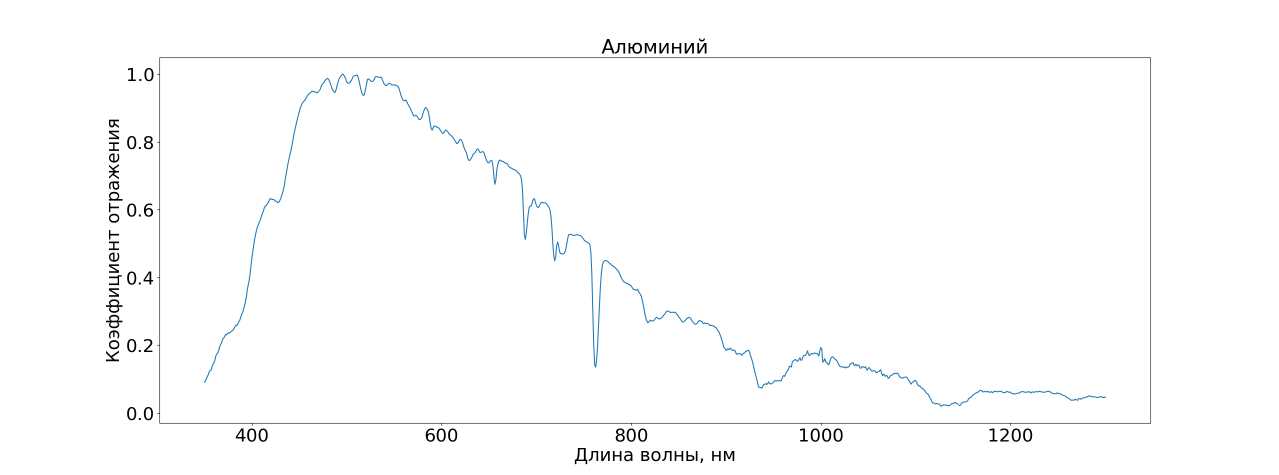
Рис. 2. Спектр алюминия

Видно, что спектры имеют большое сходство т.к. сильно зависят от источника. Когда отраженный от образца свет источника измеряется с помощью спектрометра, результиру-

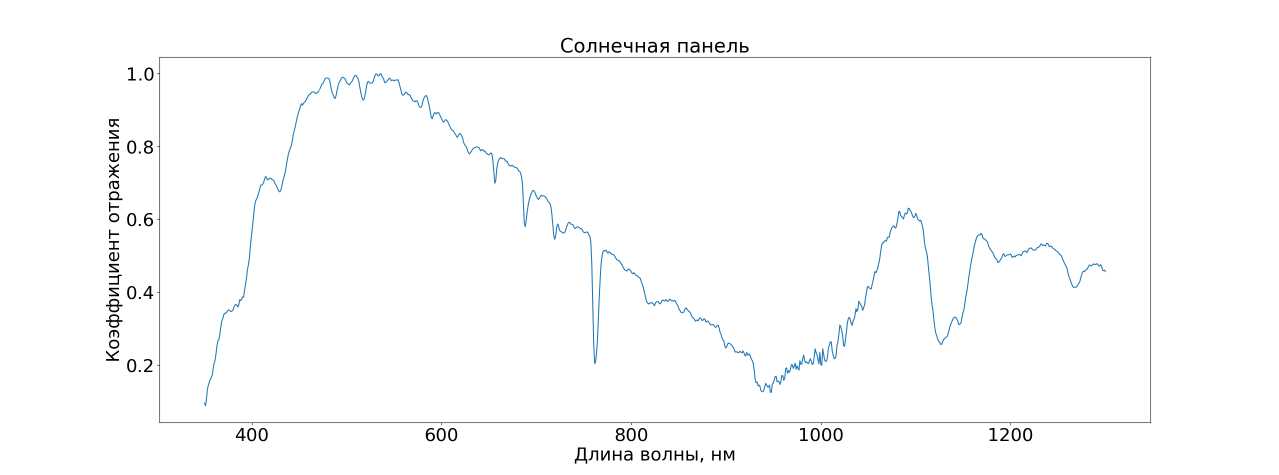
Рис. 3. Спектр солнечной панели ющий спектр является поточечным произведением спектра источника на функцию двунаправленного поверхностного рассеивания отражения, характеризующую спектр материала. Чтобы получить спектр материала, нужно поточечно поделить измеренный спектр на спектр источника. Нельзя направить срез оптоволоконного кабеля прямо на источник, так как это приведет к перенасыщению спектрометра. Поэтому спектр источника измеряется как спектр образца белого цвета, от которого отражается свет источника. На рисунках 4-5 изображены спектры источников. Стоит обратить внимание на спектр светодиодного фонаря (рис. 4). В диапазоне от 450 нм до 600 нм коэффициент отражения имеет малые значения, что при делении приведет к большим шумам коэффициента отражения в данном диапазоне длин волн. Это можно объяснить тем, что на данном диапазоне длин волн образец почти не освещен. Аналогичное можно сказать и про солнечный спектр (рис. 5), который тоже имеет диапазоны длин волн с относительно малыми значениями коэффициента отражения.

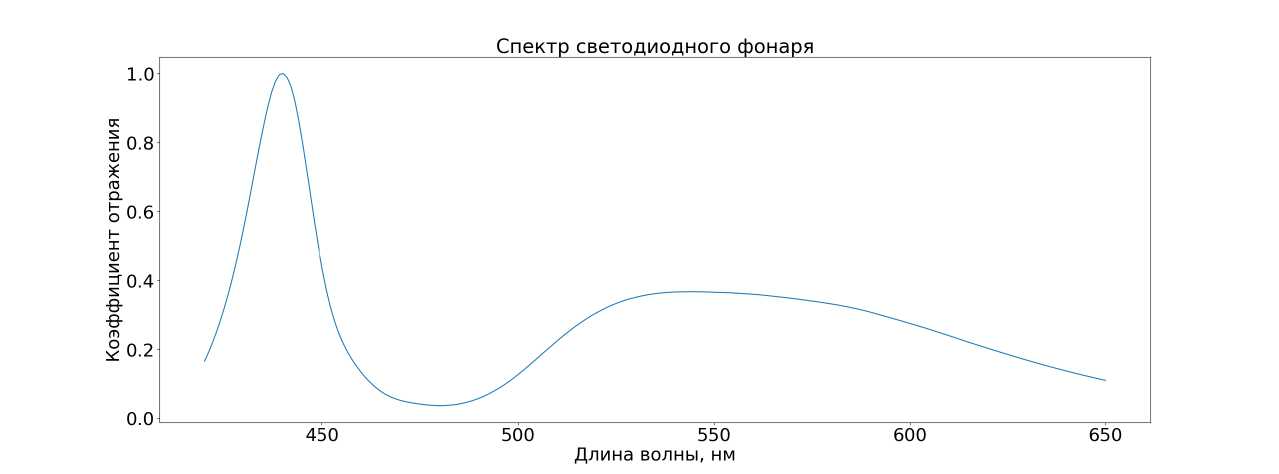
Рис. 4. Спектр светодиодного фонаря

В спектре солнечного света (рис. 5) можно заметить полосы поглощения О 2 при 750 нм и Н₂О при 950 нм и 1100 нм. Данное явление связано с поглощением атмосферы.

Следуя описанному выше алгоритму, можно получить спектры, которые слабо зависят от спектра источника и характеризуют материал. На рисунках 6-8 изображены полученные таким способом спектры. Стоит повторить, что исходные спектры были получены при солнечном свете. В диапазоне от 1000 нм заметны шумы, что соответствует относительно малой интенсивности источника на данном диапазоне.

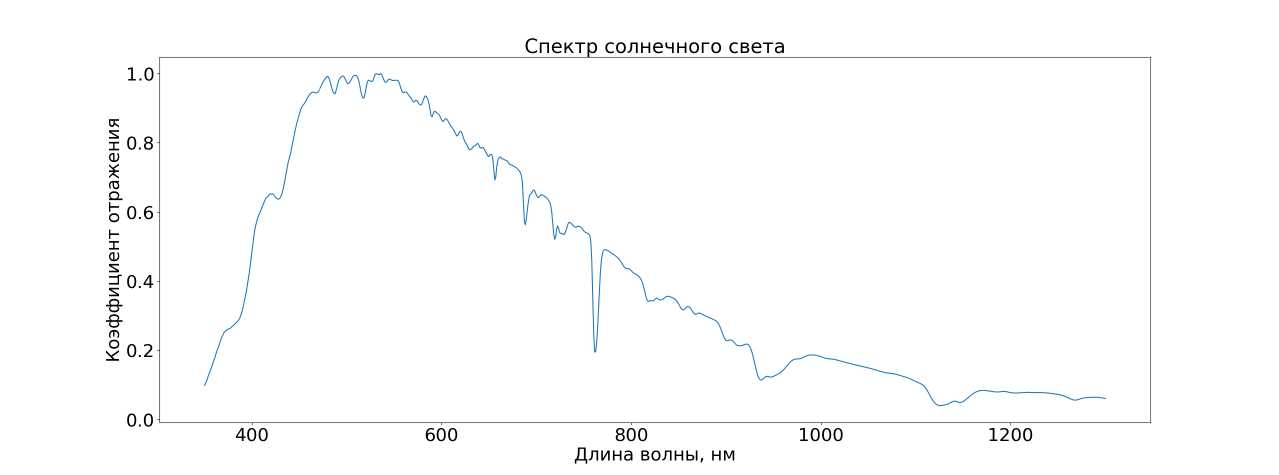
Рис. 5. Солнечный спектр

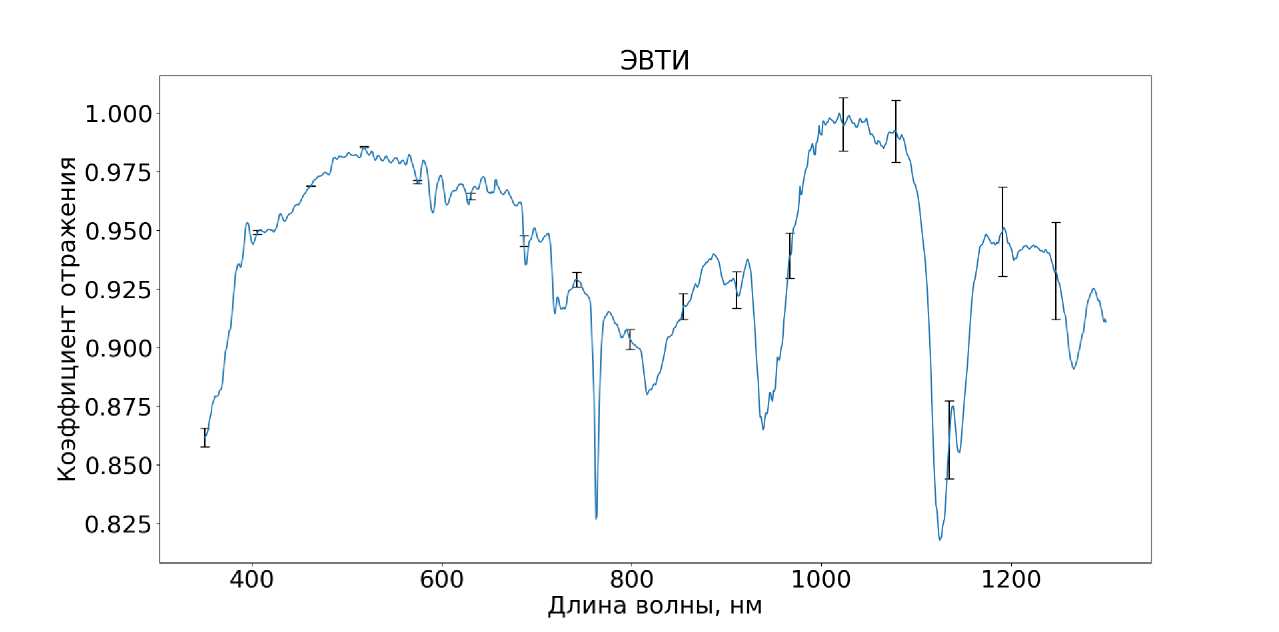
Рис. 6. Спектр ЭФТИ обработанный

В спектре алюминия и в спектре ЭВТИ заметен минимум на длине волны 750 нм, который характерен для алюминия [10].

Кремниевая солнечная панель (рис. 8) поглощает излучение в диапазоне от 400 нм до 1000 нм, где содержится большая часть солнечной энергии. Этот факт соответствует малым значениям коэффициента отражения в этом диапазоне, но на длинах волн от ЮООнм он значительно возрастает.

Кроме того, были получены индикатрисы рассеивания материалов. На рисунках 10 12 отображена зависимость коэффициента отражения от фазового угла на длине волны 550 нм. Рис. 9 иллюстрирует взаимное расположение источников света, образца и измерительного устройства.

На индикатрисе рассеяния алюминия (рис. 11) заметен один широкий максимум, соответствующий зеркальному отражению. Большая ширина экстремума объясняется грубой шлифовкой поверхности образца и, как результат, большой диффузной составляющей. Индикатриса рассеяния ЭВТИ (рис. 10) имеет несколько экстремумов и пик обратного рассеяния, так как поверхность образца сильно неоднородная и весьма негладкая.

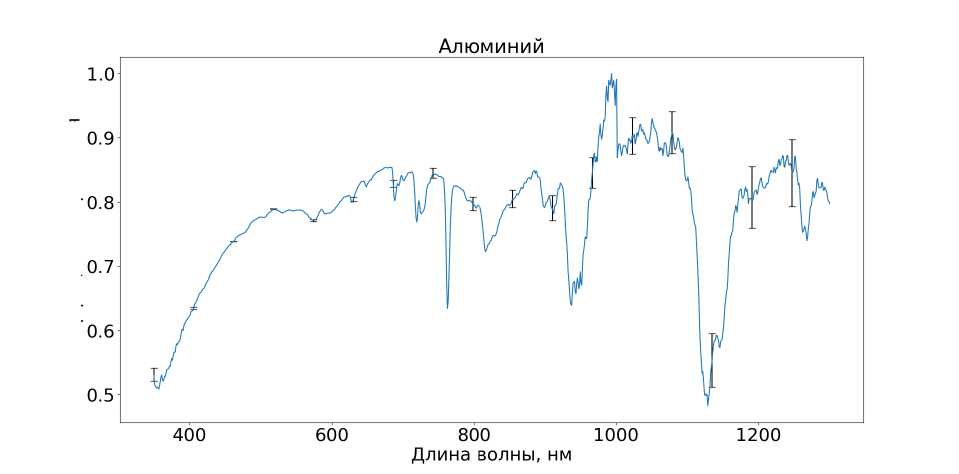
Рис. 7. Спектр алюминия обработанный

Коэффициент отражения                         Коэффициент отражения

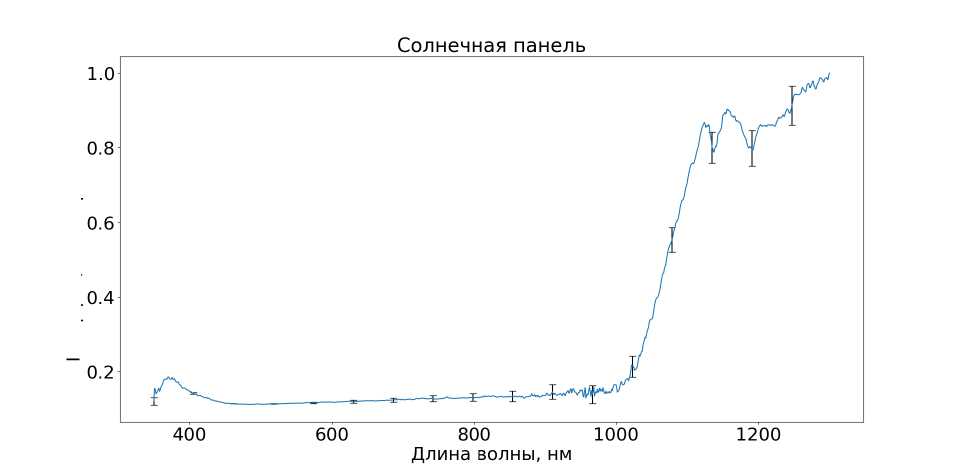
Рис. 8. Спектр солнечной напели обработанный

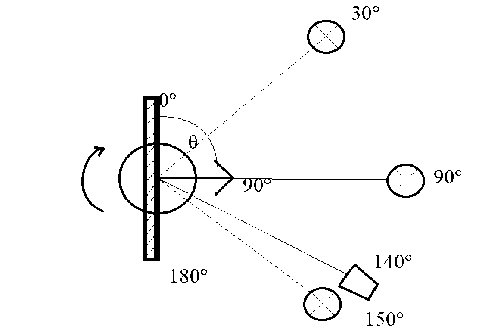
Рис. 9. Схема установки

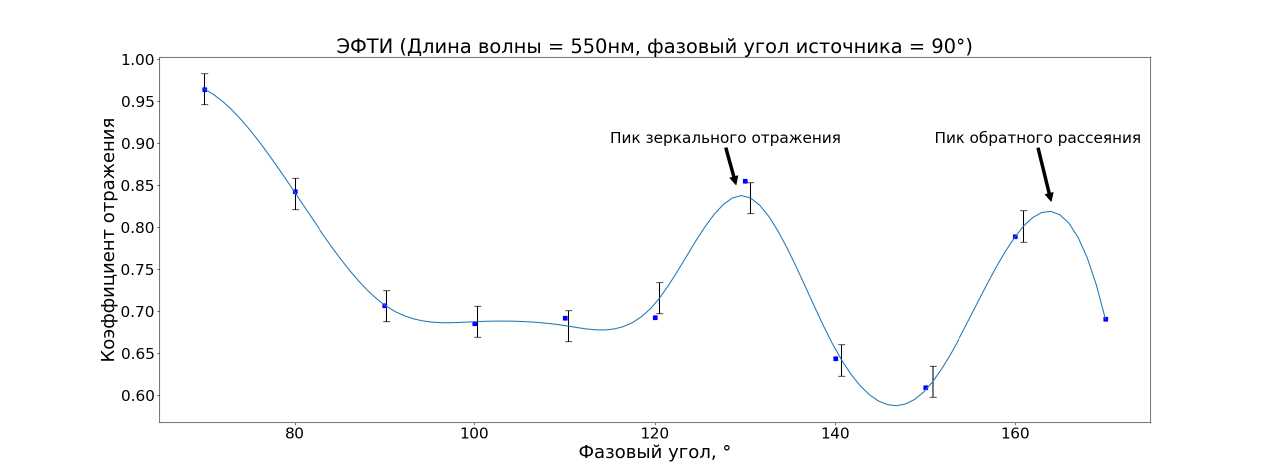
Рис. 10. Индикатриса рассеяния ЭФТИ

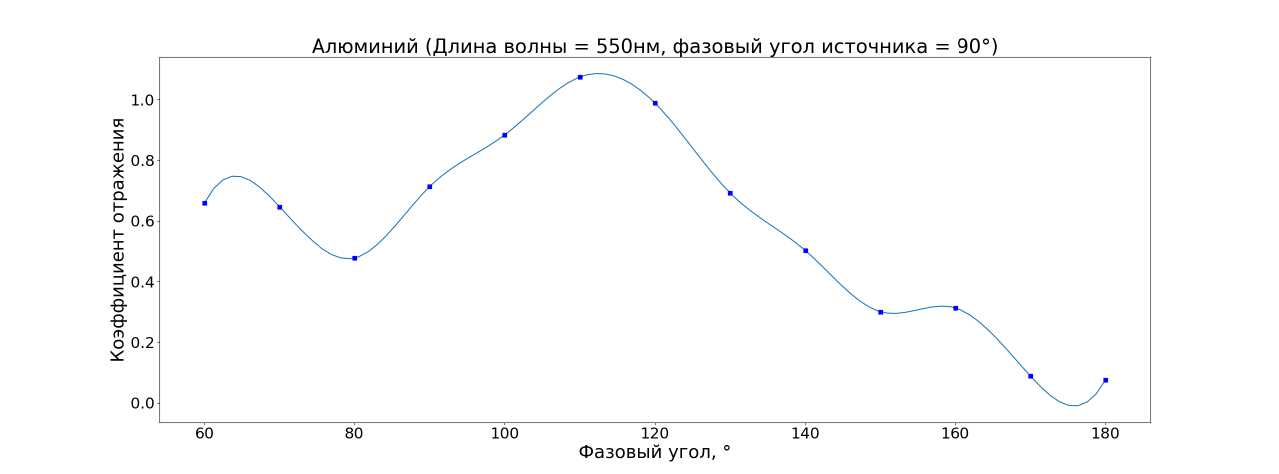
Рис. 11. Индикатриса рассеяния алюминия

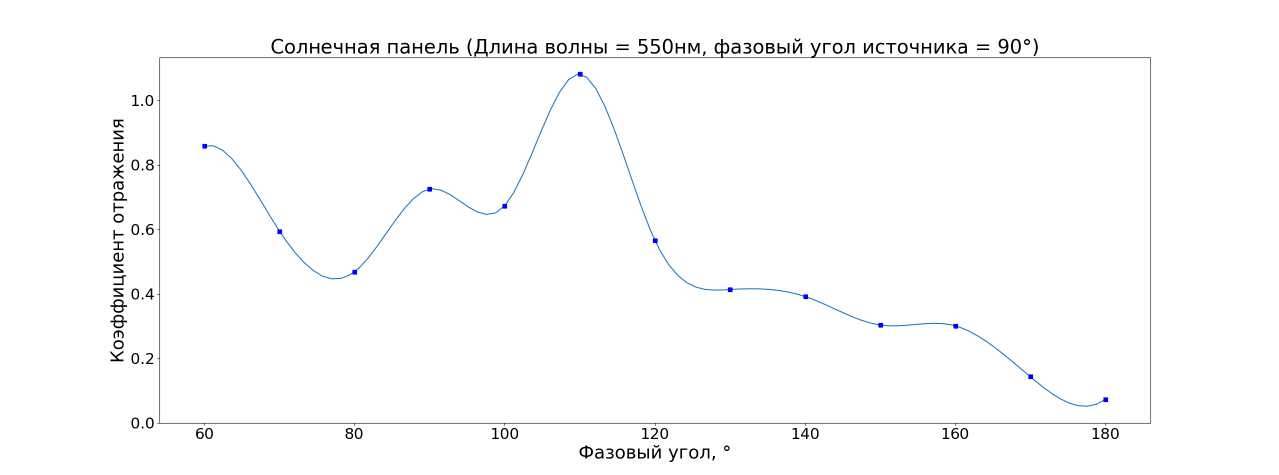
Рис. 12. Индикатриса рассеяния солнечной панели

• 3.    Метод главных компонент

Во многих прикладных задачах классификации, таких как распознавание лиц, категоризация текстов и определение материала по спектральной информации, используются данные очень высокой размерности. Для сокращения размерности и извлечения полезной информации применется метод главных компонент (Principal Component Analysis). Он позволяет перейти в пространства меньшей размерности, повышая интерпретируемость данных и минимизируя потерю информации.

Метод главных компонент является ортогональным линейным преобразованием, которое преобразует систему координат так, что максимальная проекция дисперсии данных параллельна первому координатному вектору (первая главная компонента), а дисперсия вдоль второго координатного вектора максимальна при условии ортогональности первой компоненте и так далее. Преобразование определяется набором векторов w k = (^1>"->Wn)k> которые преобразу ют каждую строку x-i матрицы данных X в вектор t- = (t1,...,t/), где Z есть размерность нового пространства и количество главных компонент.

tki = $ i • w _k , г = 1,..., п, к = 1,..., Z

Чтобы максимизировать дисперсию первый вектор весов w1 должен удовлетворять условиям максимальной дисперсии w1 = arg max

IHI=1

{?ч

= arg max INI=1

:

( Ж і • w )²

I

Или в матричной форме записи

w i = arg max IHI=1

Г w ^T X ^T Xw

(  w ^T w

.

Далее, к-я главная компонента находится путем вычисления новой матрицы данных к-1

X _k = X - : Xw _s w ^T.

s =1

Веса Шк находятся из условия максимума дисперсии матрицы Хк- wk = arg max IHI=1

{

w ^T X ^T X к w w ^T w

.

Таким образом, можем записать преобразование с помощью метода главных компонент как

Т = XW .

Метод главных компонент можно рассмотреть как следствие из сингулярного разложения. Сингулярное разложение можно представить в виде

А = U SV ^т .

где U и V являются ортогональными матрицами, составленными из собственных векторов матриц АА ^т и А^тА соответствено. S — диагональная матрица, элементы которой равны квадратному корню из положительных собственных значений матриц АА^т и А^тА. Сингулярные числа расположены на диагонали матрицы S в порядке убывания. Собственные векторы расположены в соответствующем порядке.

А

U

x ii

*

*

*

^xm 1

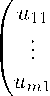
^Um 1

* * *

^U mm

( ° 1

S

O 2

*

* *

···

···

*

*

*

···

I

I • 0

«п 1

« 11

*

*

*

O 1 >0 2 >  • • • >  O_r >  0.

Сингулярное разложение также может быть представлено в следующем виде:

А = (7 1 11 11) ^ +----+ оу и _г v ^ ,

где г — количество ненулевых сингулярных чисел. Иначе, сингулярное разложение позволяет представить массив размера т х п как сумму г слагаемых. Так как и, и щ являются единичными векторами, то слагаемыми с малыми ст, можно пренебречь. Данный факт окажется полезным в дальнейшем.

Выборочной дисперсией матрицы А называете я матрица У следующего вида:

у = АА ^т

(П)

(п - 1) •

Положительные значения данной матрицы свидетельствует о положительной корреляции соответствующих величин, отрицательные означают отрицательную корреляцию, а ноль наблюдается, если они независимы.

Ковариационную матрицу с помощью сингулярного разложения можно представить в виде

X = aiUivf + CT 2- U 2 V2 +-----+ ст _г U r г) •                          (12)

Векторы и , называются главными компонентами. Первый собственный вектор U i указывает наиболее важное направление в данных.

Полная дисперсия данных равна сумме квадратов сингулярных чисел. Данный факт позволяет вычислить долю дисперсии, потерянной при отбрасывании слагаемых с малыми значениями ст, и оценить количество потерянной информации. На рисунке 13 изображена зависимость объясненной дисперсии от номера главной компоненты для спектральной библиотеки, содержащей спектры ЭВТИ, алюминия и солнечной панели.

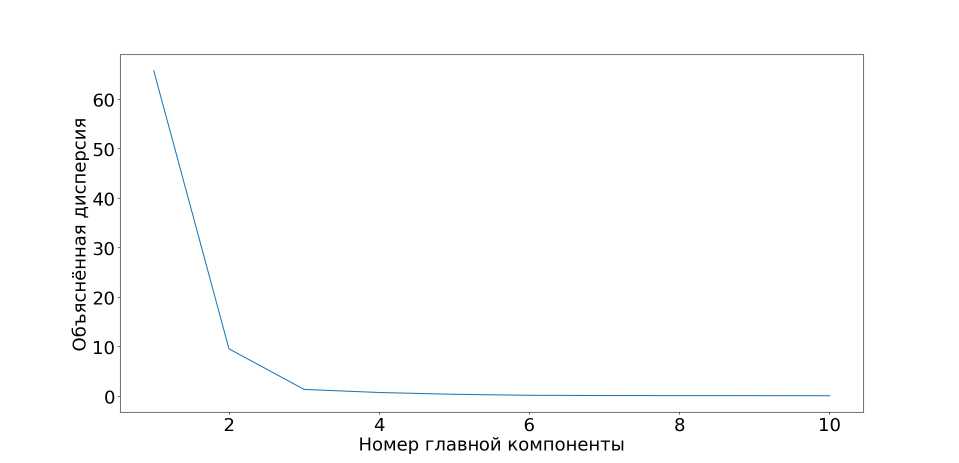
Рис. 13. Зависимость объясненной дисперсии от номера главной компоненты

Видно, что первая главная компонента носит наибольший вклад в объясненную дисперсию. Но с ростом номера компоненты это значение быстро убывает. Уже вторая главная компонента дает заметно меньший вклад, чем первая. На рисунке 14 изображено пространство размерности 2, на которое с помощью метода главных компонент отображены исходные данные спектральной библиотеки.

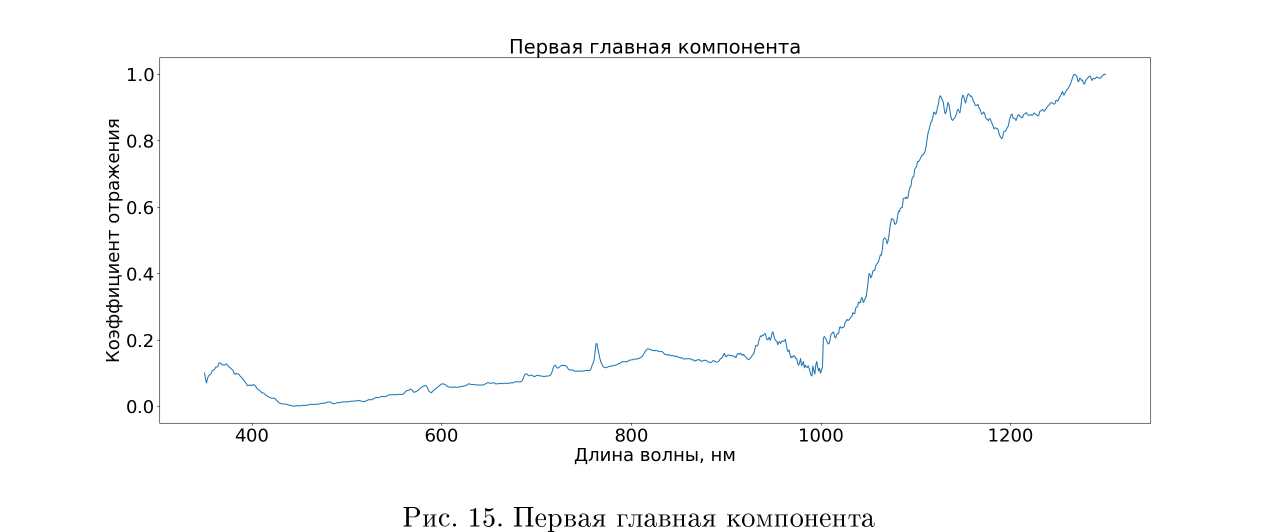
Можно заметить, что спектры алюминия и ЭФТИ хорошо отделяются от спектров солнечной панели. Наибольшая дисперсия в данных наблюдается вдоль оси первой главной компоненты. Спектры ЭВТИ и алюминия перемешаны и их сложно разделить, так как покрытие ЭВТИ изготовлено из алюминия. Иными словами, это спектры одного материала. На рисунке 15 изображена первая главная компонента. Данный вектор размерности количества каналов спектрометра определяет в многомерном пространстве спектров направление наибольшей дисперсии данных из спектральной библиотеки.

• •    Алюминий

. ЭВТИ

• •    Солнечная панель

• 4.    Оптимальная фотометрическая система

' *К •

-5                  0                  5                  10                 15

Первая главная компонента

Рис. 14. Пространство меньшей размерности

Метод главных компонент позволяет выделить направления наибольшего разброса данных. Данные направления, именуемые главными компонентами, указывают на наибольшую дисперсию в данных. Тем не менее они несут мало информации о том, какова оптимальная фотометрическая система для данного набора материалов. Из анализа главных компонент можно сделать выводы о том, в каких каналах проще всего различить спектры или, иными словами, в каком канале разница в спектральном распределении энергии для различных материалов наиболее значительна. Тем не менее в реальности телескоп не способен выделять настолько узкие спектральные полосы. Более того, даже если это было бы возможно, время экспозиции для релевантных наблюдений было бы неуместно велико. Именно поэтому фотометрические системы состоят из широкополосных и среднеполосных световых фильтров, обеспечивающих относительно малое время экспозиции. Параметры данных фильтров, а именно ширину полосы пропускания и эффективную длину волны, следует выбирать из соображений эффективного разделения спектров в новом пространстве, порожденном сверткой исходных спектров с функцией пропускания элементов фотометрической системы. Для решения данной задачи, а именно синтеза оптимальной фотометрической системы будет применен кластерный анализ.

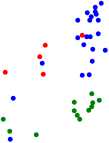
Спектральную библиотеку можно разбить на группы согласно принадлежности материалу. Таким образом, в порожденном множеством спектров пространстве, размерность которого равна количеству каналов спектрометра, присутствует несколько кластеров, количество которых равно количеству материалов в спектральной библиотеке. Спектры в этом пространстве являются точкой. Кластеры в подобном представлении находятся близко друг к другу и перемешиваются, что препятствует эффективной классификации материала (рис. 16). Кроме того, высокая размерность исходного пространства сильно снижает интерпретируемость данных и повышает вычислительную сложность любого алгоритма классификации.

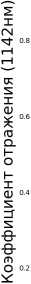
• •    Алюминий

• •    ЭВТИ

• •    Солнечная панель

  Коэффициент отражения (1181км)

Рис. 16. Исходное пространство спектров

Необходимо понизить размерность пространства исходных данных подобно тому, как это было сделано методом главных компонент. Тем не менее делать это следует решением оптимизационной задачи по минимизации некоторого функционала качества. Среднее внутрикластерное расстояние Ғ о — это среднее расстояние между элементами одного кластера (13).

_ Ег<₃ [Ш = Уз ^] Р⁽^г,Х₃ )

^ғ0 — -----ғч----г------- і --1 ^min •                            (13)

Ш г<з \^уг ^{— У}3 ^]

Для эффективной классификации следует устремить данную величину к минимуму, что приведет к локализации спектров одного материала. Другой не менее важной величиной является среднее межкластерное расстояние Fi.

„    52 г<з \^уг ^— Уз ] ^р(жг ,Xj )

F1 — ----^---;   ;--> max •

52 г<3 \^уг ^{— у}3 ^]

Как следует из названия, это величина характеризует среднее расстояние между различными кластерами. Чем оно больше, тем дальше удалены спектры друг от друга, что ведет к лучшему разграничению кластеров и точной классификации материалов. Объединением данных величин в один функционал качества можно добиться всех описанных выше свойств.

Ғ — —⁰ ^ min • ^Ғ1

Функционал качества Ғ оптимален для решения поставленной оптимизационной задачи. Оптимизационными параметрами, как уже было указано выше, следует выбрать эффек- тивные длины волн и полосы пропускания световых фильтров. Исходя из этого, можно написать постановку оптимизационной задачи.

Ғ (ж) ^ min,

I < Xi < г, г = 1 • • • 2т, Xi +i — Xi >  b, г = 1 • • • т.

Это стандартная оптимизационная задача с ограничениями в виде неравенств. Вектор ж длины 2п содержит пары границ полос пропускания световых фильтров. Число т равно количеству фильтров. Условие (17) ограничивает возможные значения границ фильтров характеристиками спектрометра. Числа I и г равны наименьшей и наибольшей длине волны спектрометра соответственно. Число b определяет минимальную ширину полосы пропускания фильтра. Данный параметр выбирается из соображений квантовой эффективности ПЗС-матрицы и малого времени экспозиции. Для оптимизации используется алгоритм внутренней точки для крупномасштабного нелинейного программирования (An Interior Point Algorithm for Large Scale Nonlinear Programming) [11].

На практике данная задача является многоэкстремальной. Это означает, что существует множество локализованных минимумов описанного выше функционала качества. Таким образом, результат сильно зависит от начального приближения решения, так как алгоритм может попасть в один из локальных минимумов, а не в глобальный. С целью учесть данную проблему применяется мультистарт. Алгоритм запускается из нескольких равномерно распределенных случайных точек. Среди решений выбирается наиболее оптимальное.

Задача решалась для 2, 3 и 5 световых фильтров. Для фотометрической системы, состоящей из 3 фильтров, оптимальными являются значения из таблицы 1.

На рисунке 17 изображены данные фильтры и первая главная компонента.

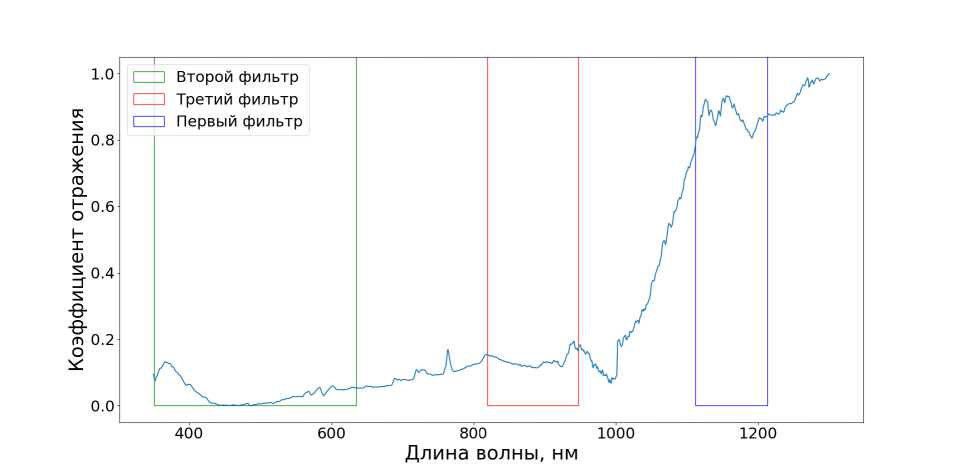
Рис. 17. Фотометрическая система, состоящая из трех фильтров

Таблица!

Оптимальные параметры фотометрической системы из 3 фильтров

Номер фильтра	Аэфф, нм	ДА, нм
1	493	284
2	883	128
3	1162	101

В подобной фотометрической системе спектры солнечной панели и алюминия с ЭВТИ хорошо разделяются. На рисунках 18-20 изображены подпространства нового признакового пространства.

Новое признаковое пространство (3 фильтра) 120

^ 80

-8-о 60

Ш 40

• •    Солнечная панель

. ЭВТИ

• •    Алюминий

0             50            100           150           200           250

Первый фильтр

Рис. 18. Признаковое подпространство первого и второго фильтров

Новое признаковое пространство (3 фильтра)

• •    Солнечная панель

. ЭВТИ

• •    Алюминий

20            40            60            80           100           120

Второй фильтр

Рис. 19. Признаковое подпространство второго и третьего фильтров

Новое признаковое пространство (3 фильтра)

о,200

В-150

50 о

• •    Солнечная панель

. ЭВТИ

• •    Алюминий

20        30        40        50        60        70        80        90

Третий фильтр

Рис. 20. Признаковое подпространство третьего и первого фильтров

Для фотометрической системы, состоящей из пяти световых фильтров, оптимальны параметры из таблицы 2.

Т а б л и ц а 2

Оптимальные параметры фотометрической системы из пяти фильтров

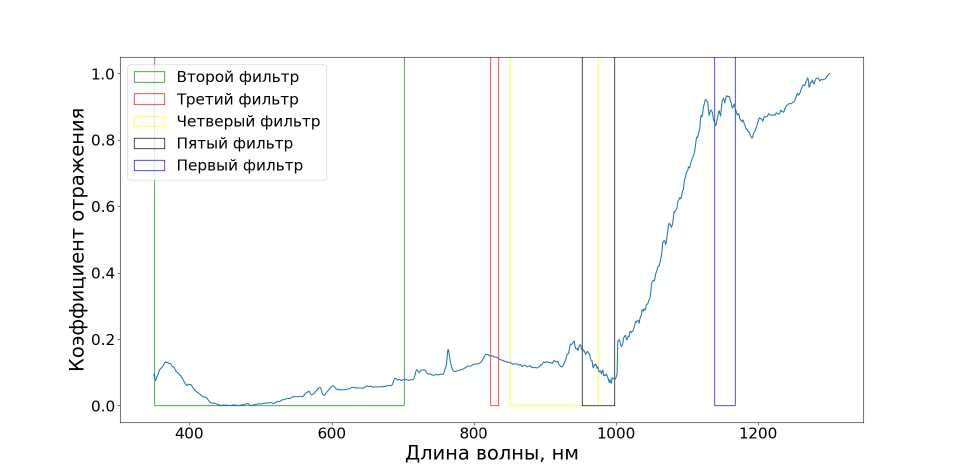
Рис. 21. Фотометрическая система, состоящая из пяти фильтров

Номер фильтра	АЭфф, нм	ДА, нм
1	526	350
2	829	12
3	912	124
4	974	46
5	1153	29

Новое признаковое пространство (5 фильтров)

Солнечная панель

ЭВТИ

Алюминий

О          50         100        150        200        250        300        350

Первый фильтр

Рис. 22. Подпространство нового признакового пространства.

Наиболее интерпретируемая система состоит из двух световых фильтров. Оптимальные параметры для данной системы указаны в таблице 3.

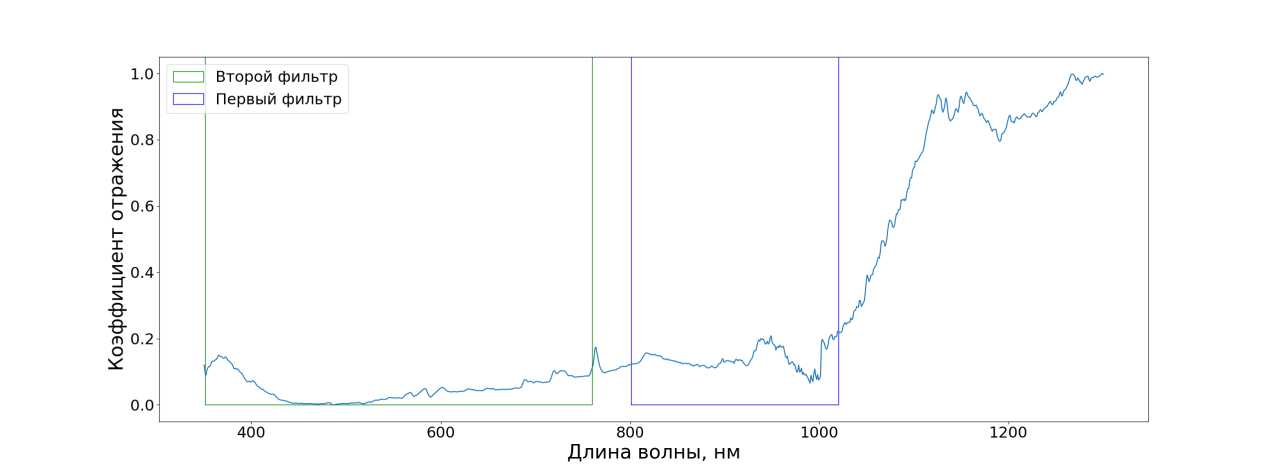
Рис. 23. Фотометрическая система, состоящая из двух фильтров

Т а б л и ц а 3

Оптимальные параметры фотометрической системы из двух фильтров

Номер фильтра	Аэфф, нм	ДА, нм
1	555	409
2	910	219

Новое признаковое пространство (2 фильтра)

0.150 |125 §"100

• •    Алюминий

. ЭВТИ

• •    Солнечная панель

50           100           150           200           250           300           350           400

Первый фильтр

Рис. 24. Новое признаковое пространство

Данная фотометрическая система позволяет наглядно увидеть работу различных классификаторов.

На рисунках 25-27 представлены области, на которые разделяют классификаторы признаковое пространство. Используются алгоритмы Random forest, k-ближайших соседей и логистическая регрессия. Данные модели работают с точностью 86%, 76% и 62% соответственно. Графики сделаны с помощью библиотеки mlxtend [12].

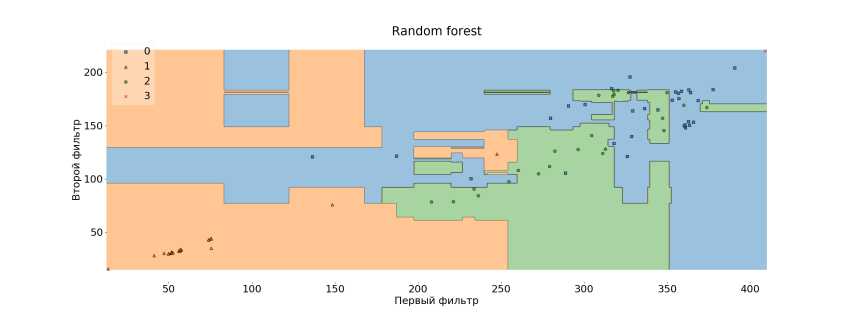
Рис. 25. Random Forest на новом признаковом пространстве

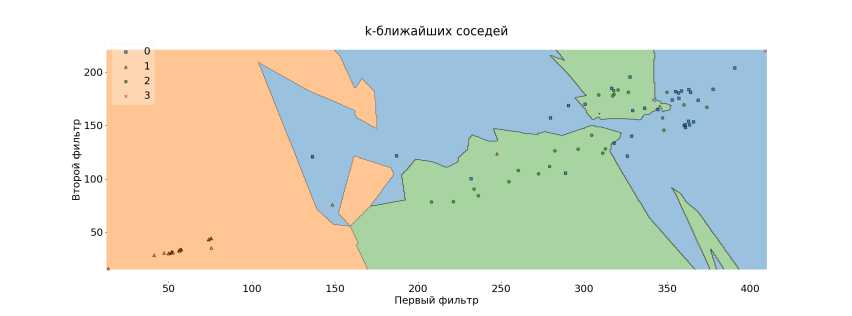
Рис. 26. к-ближайших соседей на новом признаковом пространстве

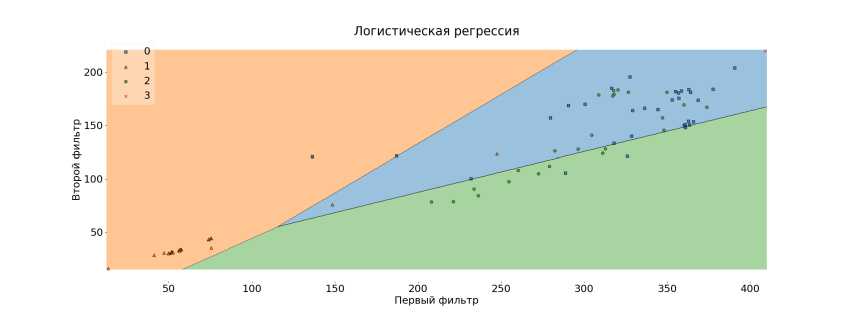
Рис. 27. Логистическая регрессия на новом признаковом пространстве

• 5.    Заключение

В данной работе рассмотрены широко используемые в космической индустрии материалы, а именно алюминий, ЭВТИ и солнечные панели. Каждый их них составляет значительную часть конструкции современного космического аппарата. С помощью спектрорадио-метра была составлена спектральная библиотека, состоящая из спектров указанных выше материалов. Кроме того, были получены фазовые характеристики образцов алюминия, ЭВТИ и солнечной панели. Полученная спектральная библиотека была проанализирована с помощью метода главных компонент с целью найти оптимальное для классификации материала признаковое пространство. Также была сформулирована оптимизационная задача, решающая вопрос нахождения оптимальной фотометрической системы. С помощью чис- ленных методов оптимизации были получены параметры для подобных фотометрических систем, состоящих из 2, 3 и 5 световых фильтров (таблица 4).

Т а б л и ц а 4

Оптимальные параметры фотометрических систем

Номер фильтра	АЭфф, нм	ДА, нм
2 световых фильтра
1	555	409
2	910	219
3 световых фильтра
1	493	284
2	883	128
3	1162	101
5 световых фильтров
1	526	350
2	829	12
3	912	124
4	974	46
5	1153	29

Системы, состоящие из большего количества фильтров, обладают большей информативностью, но ограничивают световой поток, что приводит к большему времени экспозиции. Системы, состоящие из меньшего числа, наоборот, обладают меньшим временем экспозиции, но и меньшей информативностью.