Классификация P-зубца и QRS-комплекса электрокардиосигнала в рамках корреляционной теории для задач обнаружения аритмий сердца
Автор: Галимзянов Эмиль Рустэмович, Козлов Сергей Владимирович, Хомяков Антон Вадимович, Щербакова Татьяна Филипповна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Новые информационные технологии
Статья в выпуске: 2 т.10, 2012 года.
Бесплатный доступ
В статье рассмотрены методы автоматической обработки электрокардиосигнала. Предлагаются пути расширения списка диагностируемых заболеваний за счет анализа формы зубца P, а также повышения точности обнаружения поздних потенциалов желудочков сердца. Описываются алгоритмы классификации QRS-комплекса по форме на основе оценки взаимной ковариации и оптимальной оценки параметров P-зубца на основе статистических моделей.
Автоматический анализ электрокардиограммы (экг), аритмии сердца, классификация по форме, оптимальная оценка параметров
Короткий адрес: https://sciup.org/140191550
IDR: 140191550 | УДК: 615.471
Текст научной статьи Классификация P-зубца и QRS-комплекса электрокардиосигнала в рамках корреляционной теории для задач обнаружения аритмий сердца
В связи с продолжающимся распространением сердечно-сосудистых заболеваний (ССЗ) среди населения нашей страны и постепенным снижением возраста людей, им подверженным, в производстве медико-диагностической аппаратуры наметился курс на создание современных портативных приборов, которые могли бы применяться как врачами общей практики, так и самими пациентами на дому. Такой прибор должен проводить автоматический анализ снятого электрокардиосигнала (ЭКС) и в случае обнаружения нарушения в ритме сердца выдавать информацию об этом, так как эти нарушения могут не только носить угрожающий жизни характер, но и быть предвестниками более серьезных ССЗ. Развитие телекоммуникационных систем и распространение сетей связи позволяет снабдить подобные приборы модулями связи с лечебным центром или консультирующим врачом для передачи как полной записи ЭКС, так и измеренных прибором параметров. Поэтому актуальной является разработка современных алгоритмов диагностики аритмий, которые позволят расширить список диагностируемых заболеваний в автоматическом режиме и повысить точность их обнаружения у пациентов.
К существенному недостатку большинства современных портативных приборов следует отнести ограниченный набор параметров, который используется для анализа. Чаще всего это текущая длительность интервала между соседними R-пиками и ее соотношение со средним значени- ем за некоторый период, а также параметры QRS-комплекса (см. рис.1).
Выбор в качестве диагностических параметров характеристик QRS-комплекса связан с высокой надежностью его определения, обусловленной высокой амплитудой и острым пиком. Однако медицинская практика показала, что существует необходимость анализа других элементов ЭКС.
Рис.1. Типичный кардиоцикл в норме
Ряд аритмий сердца, связанных с нарушением проводимости электрического импульса по предсердиям, проявляется в изменении P-зубца на ЭКС [1]. И поэтому для их своевременной диагностики требуется анализ формы P-зубца. Появление на ЭКГ поздних потенциалов желудочков (ППЖ) на участке конца QRS-комплекса указывает на повышенный риск развития аритмий, вызванных нарушением проводимости в желудочках сердца [2]. А значит, требуется и их анализ.
Амплитуда P-зубца сравнима с уровнем собственных шумов, ППЖ вообще представляют собой низкоамплитудные потенциалы. Поэтому анализ этих элементов ЭКС требует применения более сложных методов обработки сигналов для обнаружения нарушений в работе сердца.
Анализ формы P-зубца
Анализ формы зубца P заключается в установлении его типа, измерении амплитуды, длительности и временного положения. Можно выделить несколько основных групп методов распознавания элементов сигнала, которые находят свое применение при анализе ЭКС [3]:
-
1. Пороговые методы.
-
2. Структурные методы.
-
3. Методы сравнения с образцами.
Пороговые методы отличаются относительной простотой, но обладают невысокой устойчивостью к помехам и к изменению ЭКС у каждого пациента. Из-за этих недостатков простейшие пороговые методы находят ограниченное применение.
В основе структурных методов распознавания лежит грамматический разбор сегментированного сигнала с использованием алгоритма, базирующегося на эмпирических представлениях о структуре элементов ЭКС. К недостаткам можно отнести потерю части информации о сигнале при его сегментации, подверженность скачкообразному изменению результатов анализа при незначительных случайных отклонениях в форме входного сигнала.
При использовании метода сравнения с образцами предполагается вычисление степени похожести входного ЭКС с одним или несколькими образцами элементов. Эти образцы представляют собой модели различных видов элементов, необходимых для осуществления диагностики. Такой алгоритм может дать хорошее качество обнаружения даже в условиях значительных помех. Кроме того, одновременно с обнаружением элементов при этом решается и задача классификации их форм.
Основной проблемой для данного метода является проблема определения критерия степени схожести сигнала и образца, а также значительные вычислительные ресурсы, необходимые для проведения расчетов. Следовательно, метод сравнения с образцами целесообразно использовать для выделения элементов ЭКС, имеющих малые амплитуды, с отсутствием характерных пиков, каким является P-зубец.
Для задач анализа аритмий после установления факта наличия Р-зубца необходимо определить его параметры, для этого используются три наиболее распространенных метода:
-
- пороговый;
-
- оконный;
-
- метод оптимальной оценки параметров.
При использовании порогового метода факт начала Р-зубца фиксируется при превышении значением амплитуды ЭКС некоторого порога, а факт конца – при повторном пересечении порога. Основным его недостатком является сильная зависимость результатов от уровня шумов и искажений в сигнале.
Суть оконного метода раскрывает метод Симсона [2], который обладает следующими преимуществами: он не требует априорных сведений о сигнале и шуме, кроме того, алгоритм адаптивен к изменению уровня шума. Недостатком данного метода является то, что при малой длине следящего участка может произойти ложное срабатывание алгоритма и начало шумовых пиков может быть принято за начало искомого сигнала.
Методы оптимальной оценки параметров случайных процессов применяются в различных областях. Значение параметра в этих методах принимается исходя из выбранного качественного критерия принятия решения. Данные методы позволяют наиболее полно учесть информацию о сигнале и поэтому дают лучшие результаты.
При анализе зубца P необходимо учесть его малую амплитуду, сравнимую с уровнем собственных шумов, и отсутствие ярко выраженного пика у этого зубца, что затрудняет применение стандартных методов определения его параметров.
Наибольший интерес представляет метод сравнения с образцами. Для реализации этого метода необходимо создать некоторые образцы P-зубца. В качестве таковых предлагается использовать модели основных типов его форм, которые принято выделять в медицинской практике [4]. К ним относятся положительный, отрицательный, биполярный и расщепленный P-зубец (см. рис.2).
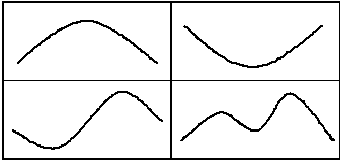
Рис.2. Типичные формы P-зубца
К уже названным достоинствам метода сравнения с образцами следует добавить адаптируемость алгоритмов сравнения в ходе анализа к форме сигнала каждого конкретного пациента, что в дальнейшем позволит провести оптимальную оценку параметров P-зубца.
Решение задачи классификации и определения параметров зубца P в методе сравнения с образцами лежит в рамках корреляционной теории. Задача решается в три основных этапа:
-
1. Построение моделей сигнала зубца P.
-
2. Принятие оптимального решения о типе зубца P, реализовавшемся в каждом кардиоцикле.
-
3. Оптимальное оценивание параметров выбранной модели.
В качестве моделей зубца P было предложено использовать полиномиальную аппроксимацию реальных классифицированных врачом-кардиологом сигналов по критерию минимума среднего квадратического отклонения. Для учета вариабельности параметров P-зубца представление модели было преобразовано к виду, инвариантному к изменениям амплитуды и длительности:
L mik = Am '^4 V^"1^ ’ (1) /=0
где A m – амплитуда P-зубца, a il – коэффициенты полинома модели, x – коэффициент учета длительности P-зубца, k 0 – положение центральной точки P-зубца, L – степень полинома, i – тип модели. Выбор степени полинома обусловливается минимизацией среднего квадратического отклонения при условии гладкости аппроксимированной функции.
Решение о виде реализовавшегося зубца P принимается на основании критерия максимального правдоподобия, который в рамках решаемой задачи представим в виде:
шением по уровню. Так как речь идет о создании портативного прибора, были использованы записи одного стандартного отведения длительностью 90 С. Были выбраны 60 записей, на которых были представлены все типы зубцов P (положительный, отрицательный, биполярный, расщепленный).
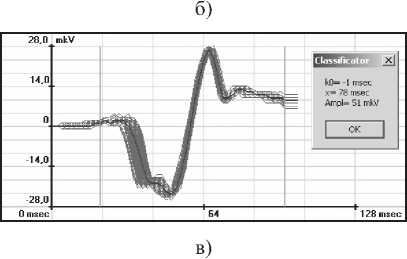
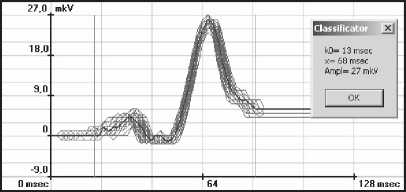
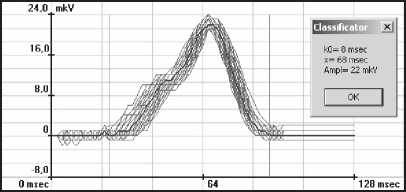
В результате работы алгоритм оптимальным образом определяет параметры модели, дающие максимальное приближение к реальному сигналу. Параметры модели принимаются в качестве оценки параметров Р-зубца. На рис.3а-г дана оценка параметров для различных типов зубца P: k0 – временное положение, x – длительность, Ampl – амплитуда.
i = arg max [Л Д6')}.(2)
/=0,4
В выражении 2 под отношением правдоподобия для i -го типа P-зубца понимается:
i к(3)
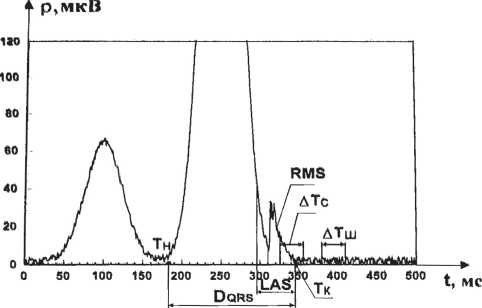
k=lk=\ и u = На предварительном этапе проводимого исследования для каждого типа P-зубца формируется модель для средних значений параметров. Далее алгоритм анализа типов и определения параметров P-зубцов состоит из следующих шагов: 1. Вычисляется отношение правдоподобия и принимается решение о наличии и типе P-зубца. 2. Находится параметр длительности зубца P. 3. Находится параметр амплитуды зубца P. 4. Вычисляются характеристики зубца P по полученным параметрам. Для реализации алгоритма использовалось приложение, разработанное в среде программирования Visual Studio .Net на языке Visual Basic. Для анализа были взяты сигналы базы данных, представленной журналом «Компьютеры в кардиологии» в 2008 г. для проведения исследования «Обнаружение и измерение вариабельности T-волн» [5]. Это записи 12 отведений ЭКГ с частотой дискретизации 500 Гц, с 16-разрядным разре- Г) Рис. 3. Оценка параметров для разных типовзубца Р: а) положительный P-зубец; б) отрицательный P-зубец; в) биполярный P-зубец; г) расщепленный P-зубец Анализ поздних потенциалов желудочков Для обнаружения ППЖ используют метод Симсона, получивший наибольшее распространение и признание в практической кардиологии. Основными свойствами, позволяющими выделить ППЖ, являются цикличность (ЭКС), высокая постоянность формы ППЖ для одного человека и их временного положения относительно самого кардиосигнала. Исходя из этих свойств представляется возможным выделить участок времени, в пределах которого могут возникать ППЖ, причем в случае их наличия форма сигнала ППЖ на данном временном интервале постоянна. Это позволяет произвести синхронное накопление сигнала ППЖ и выделить, таким образом, полезный сигнал из комплекса мышечных и аппаратурных шумов. В рамках метода Симсона ЭКС разбивают на кардиоциклы (см. рис. 1) – участки, соответствующие одному сокращению сердца. В пределах данного кардиоцикла выделяют идентичные участки возможного наличия ППЖ, которые в процессе обработки сигнала суммируются большое количество раз. Затем суммированный сигнал делится на количество суммирований – это усреднение сигнала [5-6]. Усреднение проводится отдельно для трех отведений X, Y, Z. Одно отведение при суммировании выбирается в качестве опорного. По опорному отведению определяется участок суммирования, и затем он переносится на два других отведения для суммирования сигналов по ним. Далее производится фильтрация суммированных сигналов фильтром высоких частот с частотой среза 25 Гц, это позволяет несколько подавить основной ЭКС. По полученным усредненным сигналам вычисляется амплитуда вектора ЭДС сердца – так называемый фильтрованный QRS-комплекс: U = ^U>U>uf. (4) На рис. 4 показан фрагмент фильтрованного QRS. По амплитуде вектора ЭДС вычисляются три амплитудно-временных параметра метода Симсона: DQRS – длительность фильтрованного QRS-комплекса; LAS – длительность низкоамплитудной (ниже 40 мкВ) части заднего фронта QRS-комплекса; RMS – средняя амплитуда последних 40 мС фильтрованного QRS. Решение о наличии ППЖ принимается при превышении хотя бы двумя из этих параметров фиксированных порогов: DQRS > 120 мС; LAS > 39мС; RMS < 25 мкВ. Однако при определенных заболеваниях сердца на электрокардиограмме могут содержаться различные признаки аритмии, в частности экстрасистолы, обусловленные неправильным сокращением сердца. При анализе ППЖ методом Симсона экстрасистолы представляют собой помеховые сигналы, которые существенно искажают значения параметров этого метода и, как следствие, могут приводить к ошибочным решениям о наличии или отсутствии ППЖ в ЭКС. У таких экстрасис-толических QRS-комплексов задний фронт значительно более пологий, чем у «нормальных» комплексов. Рис. 4. Фильтрованный QRS Поэтому для повышения точности обнаружения ППЖ вводится процедура отбрасывания искаженных QRS-комплексов по крутизне заднего фронта R-пика [7]. Однако, как показала практика, недостаточно процедуры отброса искаженных QRS-комплексов по крутизне, так как вариабельность формы комплексов велика и суммирование всех сигналов, кроме экстрасистол, может привести к пропуску низкоамплитудных потенциалов либо будет требовать длительного времени накопления. Поэтому предлагается ввести корреляционный метод классификации различных QRS-комплексов. Классификация кардиоциклов проводится на основе вычисления коэффициента корреляции сигналов эталона кардиоцикла E(t) и входного сигнала ЭКС (S(t)) [8]. В качестве эталонного выбирается первый «нормальный» кар , С£$(Л г) диоцикл в сигнале. При этом PesVO = ^---- ^"E^S – функция корреляционных коэффициентов; ^ E ’ ^S – среднеквадратические отклонения; b CES (t, r) = J^fX) - mE ] ■ [S'(7 - r) - ms ]dt - оценка взаимной ковариации; a, b – начало и конец QRS-комплекса соответственно. После вычисления коэффициента корреляции для конкретного кардиоцикла его сравнивают с порогом. Если он превышает порог, то j-ый кардиоцикл относиться к i-му классу (гипотеза Ni), иначе к (i + 1) классу (гипотеза Ni + 1): Ni Для выбора порога вычисляется коэффициент автокорреляции xi, или эталонного кардиоцикла: где Cx\t,^ – функция автоковариации, которая вычисляется по формуле: b Cx (t, t) = j[ST (?) - mx ] • [ST (? + r) - mx "\dt • (7) Так как сигнал i-го кардиоцикла представляет собой смесь полезного сигнала, помех и шума, то коэффициент автокорреляции не равен единице. Полученный коэффициент автокорреляции является максимальным значением порога P YlOPi . С полученным порогом проводится предварительная классификация кардиоциклов. Затем производится суммирование кардиоциклов каждого из классов и вычисляется уровень шума сигнала. Если среднеквадратическое отклонение ЭКС в области, где считается, что полезный сигнал отсутствует, оказывается больше 4 мкВ [7], это означает, что полученного количества кардиоциклов недостаточно для суммирования. Поэтому значение Pnop уменьшается, и процедура классификации проводится с новым порогом. Таблица 1. Параметры ППЖ для различных классов Классы (кол-во комплексов) DQRS. LAS, RMS, ППЖ 1 (100) 159 38 23 Есть 2(100) 156 33 30 Нет 3 (80) 144 27 38 Нет 4(80) 140 24 42 Нет 1+2 (50+50) 160 39 25 Есть 1+2(60+60) 160 37 24 Есть 1+2(70+70) 161 37 24 Есть 1+2(80+80) 160 36 25 Есть 1+2(90+90) 158 35 26 Нет 1+3 (100+50) 158 37 24 Есть 1+3 (50+50) 154 34 27 Нет 1+4(50+50) 152 33 29 Нет 1+2+3(40+40+40) 155 35 27 Нет 1+2+3(50+50+50) 158 38 23 Есть 1+2+3 (60+60+60) 153 35 26 Нет 1+2+4(40+40+40) 154 34 27 Нет На основе вышеизложенного метода был разработан алгоритм классификации кардиоциклов и анализа поздних потенциалов желудочков сердца. С помощью которого была произведена обработка ЭКС различных пациентов. В рамках вышеизложенного алгоритма было произведено разделение кардиоциклов на классы и их поклассовый анализ. Усреднение производилось не только в каждом отдельном классе, но и при различных сочетаниях классов, и различных количествах суммированных комплексов. Результаты обработки ЭКС для одного из пациентов приведены в таблице 1. Проведенный эксперимент показал, что параметры метода Симсона в отдельных классах удовлетворяют критериям наличия ППЖ. Так же было проверено, не превышает ли уровень шума после суммирования в каждом из классов установленного порога в 4 мкВ (см. таблицу 2). Таблица 2. Значения уровня шума сигнала для различных классов Классы (число комплексов) Уровень шума, мкВ 1 (100) 3,518 2(100) 3,456 3 (80) 3,735 4 (80) 3,758 1+2 (50+50) 3,469 1+2 (60+60) 3,192 1+2 (70+70) 2,904 1+2 (80+80) 2,773 1+2 (90+90) 2,698 1+3 (100+50) 2,834 1+3 (50+50) 3,685 1+4(50+50) 3,629 1+2+3(40+40+40) 3,049 1+2+3 (50+50+50) 2,984 1+2+3 (60+60+60) 2,675 1+2+4 (40+40+40) 2,986 Как видно из таблицы 2, во всех рассмотренных случаях уровень шума сигналов не превышает установленного порога. Исходя из полученных результатов можно сделать вывод, что, используя предложенный метод, возможно достоверное определение параметров ППЖ при меньшем количестве суммированных комплексов и более высоком уровне шума сигнала. Заключение Полученная методика обработки ЭКС, а также реализующие ее алгоритмы анализа формы зубца P и анализа ППЖ позволят расширить список диагностируемых заболеваний за счет обнаружения нарушений в проводимости предсердий и повышения уровня достоверности принятия решения о наличии ППЖ. Использование описанных алгоритмов позволит создать современный анализатор аритмий и вовремя предупреждать о возможном появлении серьезных заболеваний, угрожающих жизни пациента.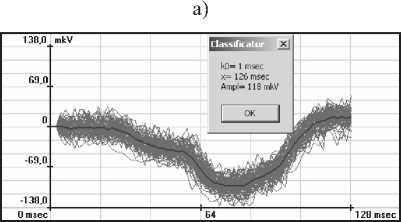
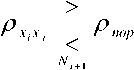
Список литературы Классификация P-зубца и QRS-комплекса электрокардиосигнала в рамках корреляционной теории для задач обнаружения аритмий сердца
- Струтынский А.В. Электрокардиограмма: анализ и интерпретация М.: Медпресс-информ, 2002. -224 с.
- Simpson M.B. Use of signals in the terminal QRS complex to identify patients with ventricular tachycardia after myocardial infarction//Circulation. Vol. 64, 1981 -P. 235-242.
- Сахаров В.Л. Методы и средства анализа медикобиологической информации. Таганрог: Изд. ТРТУ, 2001. -70 с.
- Catalano J.T., Guide to ECG Analysis. Lippincott, 2002. -479 р.
- http://physionet.org/challenge/2008/
- Иванов Г.Г., Грачева С.В., Сыркина А.Л. Электрокардиография высокого разрешения. М.: Триада-Х, 2003. -304 с.
- Седов С.С. Система анализа низкоамплитудных потенциалов сердца на основе статистического алгоритма поиска характерных точек электрокардиосигнала. Дисс. к.т.н. Казань: КГТУ, 1998. -104 с.
- Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа, 2000. -462 c.