Классификация поверхностей в 3D-модели желудочков сердца методами машинного обучения

Унифицированное представление анатомии желудочков сердца, не зависящее от конкретного субъекта, является ценным инструментом для обработки данных в кардиологии. Такой инструментарий полезен для стандартизированной визуализации сердца; интеграции данных, полученных с помощью различных методов измерения; оценки региональной функции сердца; описания локального положения зоны интереса в сердце, например, зоны поздней активации миокарда или расположения электрода кардиостимулятора; построения математических моделей в кардиологии.

Наиболее популярным примером такого представления является 17-сегментная модель левого желудочка (ЛЖ), предложенная Американской кардиологической ассоциацией [1], разбивающая ЛЖ на анатомически и функционально значимые сегменты. Хотя ее легко применять на практике, она дает дискретное представление ЛЖ и не охватывает правый желудочек (ПЖ). В 2018 году была предложена универсальная система координат (Universal Ventricular Coordinates, UVC) для построения геометрических моделей желудочков сердца [2]. Такой подход является более общим, поскольку он обеспечивает непрерывную параметризацию как ЛЖ, так и ПЖ. Система UVC характеризует каждую точку в трехмерном теле желудочков сердца четырьмя координатами, каждая из которых принимает значения в отрезке [0, 1]. Апико-базальная координата описывает положение точки желудочков относительно длинной оси, трансмуральная координата описывает положение в толще стенки желудочка и определяет близость к внутренней/внешней поверхностям желудочков, угловая координата – задает угол вращения вокруг длинной оси, трансвентрикулярная бинарная координата указывает, в каком желудочке находится точка. Подобная параметризация существует и для предсердий [3]. В дальнейшем были предложены альтернативные и/или усовершенствованные решения [4, 5].

Для построения координатных систем желудочков требуется предварительная классификация элементов полигональной сетки, полученной на основе сегментации изображений сердца. Должны быть выделены и промаркированы классы, соответствующие поверхностям желудочков: внутренняя поверхность полостей

ЛЖ и ПЖ (далее по тексту будем обозначать эндо поверхности), внешняя поверхность желудочков (далее эпи ) и отдельно базальная поверхность желудочков (далее основание ). Перечисленные поверхности показаны на рис. 1 слева. Заметим, что классы эпи и эндо ЛЖ и ПЖ не пересекаются между собой и граничат только с основанием (рис. 1 справа). Это условие является необходимым для корректного построения координатной системы желудочков [4].

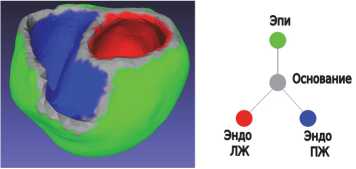
Рис. 1. Левая панель: разметка поверхностной полигональной сетки желудочков сердца. Правая панель: схема классификации полигональной сетки желудочков в виде компонент связности графа

Ранее для решения задачи классификации точек в трехмерных объектах было предложено два подхода. Первый работает с такими структурами данных, как облака точек, то есть из вершин трехмерного объекта формируется облако точек и подается на вход модели машинного обучения, которая должна классифицировать каждую точку. Данный подход был предложен авторами модели PointNet [6] и в дальнейшем усовершенствован в моделях PointNeXt [7], Mini-PointNetPlus [8] и др. Альтернативным подходом является использование полигональных сеток напрямую, это позволяет использовать не только вершины, но и соединяющие их рёбра и грани. Данная идея была использована в основе модели MeshCNN [9], а также её более современных вариантов, таких как HalfedgeCNN [10] и др.

Оба подхода показывают высокую точность классификации на крупных синтетических наборах данных, таких как ModelNet и COSEG [11, 12], каждый из которых включает в себя 1000 и более объектов. Однако, как показано в [13] на примере PointNet, на клинических данных с меньшим размером тренировочной выборки их точность существенно снижается. Это объясняется двумя основными факторами: во-первых, исследования [11] демонстрируют необходимость значительного объема данных для стабильной работы 3D-моделей; во-вторых, в обоих случаях каждый трехмерный объект представляет собой один элемент в тренировочном наборе данных, и увеличение входящих в данный объект составляющих, например количества вершин, влечет за собой значительный рост количества обучаемых параметров и требуемой памяти, что усиливает риск переобучения на малых выборках [14].

В предыдущей работе [13] мы предложили следующий подход для решения задачи классификации поверхностей желудочков сердца: эпи, эндо ЛЖ, эндо ПЖ, на поверхностной сетке в условиях небольших тренировочных выборок. Сведем задачу к задаче многоклассовой классификации точки на поверхности сетки. Для каждой вершины полигональной сетки закодируем ее окрестность с помощью функции расстояния со знаком и будем передавать на вход модели машинного обучения такую окрестность. Предложенный подход объединяет преимущества представленных выше методов, так как он использует информацию, заложенную в вершинах, рёбрах и гранях поверхностной сетки в ходе кодирования, а также не нуждается в больших наборах данных, так как экземпляром тренировочной выборки является точка, а не весь трехмерный объект целиком, что на порядки величин повышает объем обрабатываемой информации. В данной работе мы продолжаем исследование в нескольких направлениях. Во-первых, мы добавляем сравнение большого количества классификаторов. В предыдущей работе использовалась полносверточная нейронная сеть FCNN, здесь же мы также используем более сложные нейронные сети и более простые классификаторы из пакета scikit-learn. Далее, данная работа имеет более практический фокус: сегментация поверхностей желудочков сердца для построения координатной системы. Отсюда, во-вторых, в задачу классификации также добавлена поверхность основания, необходимая для построения координатной системы желудочков. В-третьих, мы предлагаем алгоритм для проверки необходимого условия взаимного непересече-ния классов (классы эпи, эндо ЛЖ и ПЖ не имеют общих границ и граничат только с основанием). В-четвертых, мы предлагаем детерминированный графовый алгоритм для исправления некоторых потенциальных ошибок классификации. Наконец, классификация проводится на выборке пациентов с ХСН из закрытого да-тасета российского медицинского центра.

Цель исследования . Сравнить качество классификации поверхностей желудочков сердца (эпи, эндо ЛЖ, эндо ПЖ) в рамках предложенного подхода для базовых моделей машинного обучения: классификаторы, содержащиеся в пакете scikit-learn, а также нейронные сети с архитектурами FCNN, U-Net, ResNet. Разработать метрику для оценки качества классификации с точки зрения задачи построения координатной системы на желудочках сердца. Разработать дополнительный алгоритм улучшения результатов классификации.

Материалы и методы исследования Популяция

В исследовании использовались ретроспективные данные 37 пациентов с хронической сердечной недостаточностью (ХСН) из исследования [15]. Всем пациентам была проведена компьютерная томография (КТ) для визуализации сердца, легких, торса. Серии, полученные с помощью сканера (Somatom Definition 128, Siemens Healthcare, Германия), импортировались в специальную программу Wave версии 2.14 (Amycard,

EP Solutions SA) для полуавтоматической реконструкции трехмерной геометрии желудочков сердца в виде тетраэдральной сетки. Для каждой из полученных геометрий была проведена классификация поверхностей эпи, эндо ЛЖ, эндо ПЖ и основания желудочков врачом функциональной диагностики высшей категории и построены полигональные сетки. Выборка разделена на обучающую (n_train = 19) и валидационную (n_test = 18). Для финального тестирования был использован независимый набор данных 20 пациентов с ХСН (n_test), обследованных в том же учреждении по идентичному протоколу, но в более поздний период. Так как алгоритмы классификации работают на отдельных точках, обучающая выборка была представлена 152000 точками, валидационная – 159452 точками, а тестовая – 232549 точками (подробности ниже).

Извлечение признаков для обучения и тестирования

В качестве признаков для классификации точки полигональной сетки используется значение функции расстояния со знаком в окрестности этой точки. В качестве окрестности точки ( x , y , z ) используется равномерная прямоугольная сетка (uniform rectilinear grid) с центром в этой точке. Для построения окрестности сначала задаем куб с центром в точке ( x , y , z ) и стороной a . Затем в этом кубе строим равномерную прямоугольную сетку с шагом h = a /( N – 1), где N – количество точек на каждой стороне куба. Далее для каждой точки p из окрестности рассчитывается расстояние со знаком от точки p до поверхности фигуры, задаваемой полигональной сеткой. Знак положительный, если точка p лежит снаружи фигуры, и отрицательный, когда точка p лежит внутри фигуры. Для вычисления функции расстояния со знаком используется библиотека [16]. В данном исследовании использовались кубические окрестности со стороной куба a =20, что соответствует 2 cм. Количество точек на каждой стороне куба в равномерной прямоугольной сетке задано N = 16, следовательно, шаг в сетке окрестности h = 115 мм. Пример такой построенной окрестности можно увидеть слева на рис. 2.

Доля точек разных классов в данных отличается. В среднем по обучающей выборке в одной полигональной сетке желудочков к эпи относятся 3982 точки (47 %), к эндо ЛЖ – 2234 точки (27 %), к эндо ПЖ – 1684 точки (20 %), к основанию – 528 точек (6 %). Для балансировки классов в обучающей выборке применена следующая схема: из каждой полигональной сетки для каждого класса извлекаются 2000 точек методом случайного выбора с повторениями. Чтобы классификаторы научились определять принадлежность точки к той или иной поверхности желудочков независимо от поворота желудочков в окружающем пространстве и независимо от размера желудочков, окрестности точек в обучающей выборке были случайно модифицированы. А именно, для каждой точки ее окрестность случайно поворачивалась вокруг центра и масштабировалась. Три угла поворота извлекались из равномерного распределения на отрезке [–0,5; 0,5] радиан, масштабирующий коэффициент извлекался из равномерного распределения на отрезке [0,97; 1,03]. В предыдущей работе данные диапазоны распределений углов поворотов и масштабирующего коэффициента были выделены как оптимальные (ми-нимизурующие ошибку на тестовой выборке) для аналогичной задачи [13]. На рис. 2 справа показаны возможные варианты случайно масштабированных и повернутых кубических окрестностей.

При построении валидационной и тестовой выборок использовались все точки в полигональных сетках без поворота и масштабирования.

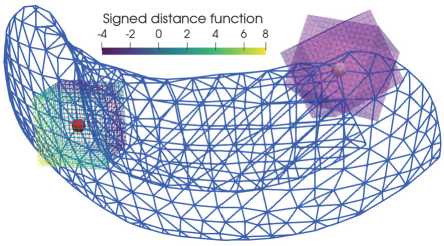
Рис. 2. Демонстрация процедуры извлечения признаков.

Синим представлена полигональная сетка базального отдела передней стенки ЛЖ (остальные части желудочков сердца были отсечены для наглядности). Слева красным обозначена точка на эпи поверхности. Вокруг красной точки построена прямоугольная сетка, цвета точек на прямоугольной сетке содержат значение функции расстояния со знаком, в соответствии с цветовой картой вверху рисунка. Справа серым обозначена точка на основании ЛЖ. Вокруг нее построены две прямоугольные окрестности розового цвета с разным масштабом и углами поворота

Классификация

Задача классификации точек полигональной сетки решалась с помощью 8 архитектур нейронных сетей и 10 классификаторов из пакета scikit-learn [17]. Рассмотренные нейронные сети включают в себя ResNet-16, ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152 [18], U-Net [19], а также полносверточную сеть FCNN [13]. На вход нейронным сетям подавались тензоры размера batch_size 1×16×16×16, где batch_size – размер батча для оптимизатора. Оригинальные архитектуры моделей типа ResNet и U-Net были модифицированы, чтобы принимать на вход трехмерные данные. Для этого двухмерные свертки и слои пулинга (англ. pooling) были заменены на трехмерные и входной слой каждой из моделей был изменен для соответсвующего размера тензора. Помимо этого, в архитектуре U-Net был вырезан последний слой кодировщика, а во всех остальных слоях увеличено значение дополнения (англ. padding) на единицу по каждой оси. Данные изменения необходимы, так как оригинальная модель рассчитана на работу с изображениями 572×572 и не способна обработать тензоры низкого размера 16×16. Каждая из моделей была обучена на протяжении 1000 эпох с оптимизатором ADAM и бинарной перекрестной энтропией (англ. binary cross-entropy) в качестве функции ошибки. При обучении нейронных сетей использовалась L2-регуля-ризация, также функция потерь рассчитывалась не только на обучающей, но и на валидационной выборке. Для каждой сети выбирался набор весов с наименьшим значением функции потерь на валидаци-онной выборке.

Мы рассматривали следующие классификаторы из пакета scikit-learn: дерево решений (англ. decision tree, DTree), случайный лес (англ. random forest classification, RF), логистическую регрессию (англ. logistic regression, LR), метод k-ближайших соседей (англ. k-nearest neighbors algorithm, k-NN), модель наивного байесовского классификатора (англ. naive bayes classifier, NB), перцептрон (англ. Perceptron), линейный дискриминантный анализ (англ. linear discriminant analysis, LDA), а также три варианта метода опорных векторов (англ. support vector machines, SVM): метод опорных векторов, использующий радиальную базисную функцию (англ. C-support vector classification, SVC), линейный метод опорных векторов, минимизирующий функцию потерь Hinge Loss (linear support vector classification, LSVC) и линейный метод опорных векторов, относящийся к классу SGDClassifier (SVC-SGD). Для передачи на вход этим алгоритмам тензоры были векторизованы (flattened) к размеру batch_size×4096.

Улучшение результатов классификации

Используемые модели машинного обучения решают абстрактную задачу классификации точки поверхностной сетки по значению функции расстояния в окрестности этой точки. Стандартные модели не приспособлены под предметную область классификации точек на поверхности сердца. Поэтому классификаторы допускают ошибки, которые можно исправить простым графовым алгоритмом. Этот алгоритм обработки результата классификации назовем GraphAlg и опишем ниже. Представим поверхностную сетку сердца M , состоящую из вершин V , ребер E и граней F в виде неориентированного вершинно-раскрашенного графа G =( V , E , γ ), где каждое ребро e ij € E соответствует ребру, которое соединяет две вершины v i € V и v j € V . Функция у : V ^ K сопоставляет каждой вершине цвет (класс), определенный моделью машинного обучения, где K – множество классов. Обозначим через C k множество вершин, отнесенных моделью МО классу k , так что C k ={ v i € V : y ( v ) = k€K }. Определим также подграфы C k графа G как подграфы, получающиеся из G после удаления всех вершин, не отнесенных к классу k , и инцидентных им ребер. Алгоритм обработки будет выглядеть следующим образом:

• 1.    Для каждого класса i € K выполнить

• 2.    Найти components — компоненты связности подграфа Ck

• 3.    Если количество компонент связности больше 1, то

• 4.    Отсортировать компоненты связности по убыванию количества вершин

• 5.    Для каждой компоненты связности component из components, кроме компоненты с наибольшим количеством вершин, выполнить

• 6.    Найти класс k, который чаще всего встречается среди соседей подграфа component в исходном графе G

• 7.    Присвоить класс k каждой вершине, содержащейся в component

На каждой итерации цикла в строке 2 количество компонент связности в соответствующем подграфе G i уменьшается до единицы, при этом количество компонент связности в остальных подграфах G i : j€K , j ^ i остается неизменным. Таким образом, после выполнения алгоритма каждый класс будет представлен одной компонентой связности.

Обратим внимание, что в зависимости от результатов классификации алгоритм GraphAlg может работать неправильно. Его стоит применять при достаточно высокой точности классификации. Строгий поиск условий, при которых результат алгоритма верный, выходит за рамки данной статьи. Однако мы продемонстрируем эффективность алгоритма эмпирически, с помощью теста, описанного ниже.

Метрика качества классификации

Одним из главных условий является разделение в ходе классификации эпи и эндо поверхностей ЛЖ и правого ПЖ. В качестве разделяющей границы для данных классов используется поверхность основания желудочков. Это значит, что модель машинного обучения должна провести классификацию точек поверхностной сетки сердца так, чтобы выполнялось следующее топологическое условие:

• 1)    каждый из классов был представлен ровно одной компонентой связности,

• 2)    классы эпи, эндо ЛЖ и эндо ПЖ не имели общих границ между собой,

• 3)    класс основания имел общую границу с каждым из остальных классов (рис. 1).

Определим величину GraphTest(G, C, K) € {0, 1} как величину, равную 1, если классификация удовлетворяет указанным условиям, и 0 в ином случае. Определим Graph-score как среднее значение GraphTest по рассматриваемой выборке. Приведем псевдокод алгоритма вычисления GraphTest. Определим основания ЛЖ и ПЖ как base K.

• 1.    Для каждого класса i € K, кроме base, выполнить

• 2.    Вычислить neighbour_classes – множество классов, соседствующих с вершинами класса i и отличных от i

• 3.    Если размер neighbour_classes больше 1, то

• 4.    Вернуть 0

• 5.    Если base не содержится в neighbour_classes, то

• 6.    Вернуть 0

• 7.    Вернуть 1

Сравнение классификаторов

Построенные классификаторы сравнивались по трем параметрам: точности классификации относительно экспертной разметки; выполнению топологического условия, определенного выше; и производительности классификаторов. Качество классификации оценивалось стандартными метриками accuracy, precision, recall, F1-score. Для получения итоговой мультиклассовой метрики мы рассчитывали значения для каждого класса по отдельности, а затем вычисляли среднее значение метрики между классами. Из-за дисбаланса классов мы ориентировались на величину F1-score. Топологические условия оценивались метрикой Graph-score.

F1-мера оценивает точность классификации отдельных точек сетки, и в контексте построения координатных систем желудочков небольшие отклонения в точности определения границ между классами не критичны, поскольку оригинальная экспертная сегментация также содержит элемент субъективности. В то же время метрика Graph-score имеет принципиальное значение, поскольку нарушение топологического условия делает невозможным корректное построение координатной системы желудочков. Таким образом, идеальный классификатор должен демонстрировать высокое значение F1-score и Graph-score, равную 100%. Приоритетным является именно выполнение топологического условия, даже если это приводит к некоторому снижению F1-score.

Лучшие модели, отобранные по F1-score и Graph-score, прошли дополнительную проверку на тестовой выборке .

Оценка производительности классификаторов – времени, используемого для классификации, происходила следующим образом. Случайным образом выбирались 1000 точек из всей выборки, и выполнялась их классификация, эта процедура выполнялась 100 раз для каждого классификатора. Итоговая производительность классификатора вычислялась как среднее количество секунд среди 100 процедур. В случаях, когда классификация может выполняться на графическом ускорителе (GPU), были рассмотрены отдельно производительность на GPU и производительность на центральном процессоре (CPU).

Результаты исследования и их обсуждение

На валидационной выборке наибольшая точность классификации поверхностных сеток достигается глубокими нейронными сетями семейств моделей ResNet и U-Net. Модель ResNet-101 c 93 600 067 обучаемыми параметрами показала наивысший показатель F1-score (табл. 1). Однако менее глубокая модель FCNN продемонстрировала сопоставимое качество классификации, имея 477 412 обучаемых параметров, что в 196 раз меньше. Более того, классификаторы, основанные на методе опорных векторов (SVC) и случайного леса (RF), также показали сопоставимые результаты, отклоняясь в значениях метрик качества классификации не более чем на 3 % от ResNet-101. Метод k-ближайших соседей (k-NN) и дерево решений (DTree) достигли схожих показателей F1-score: 85,81 % и 85,58 % соответственно (табл. 1).

Несмотря на высокие показатели F1-score, модели продемонстрировали низкие значения метрики Graph-score. Классификация поверхностной сетки желудочков с низким показателем данной метрики непригодна для построения координатной системы.

После применения алгоритма улучшения классификации для всех рассмотренных выше классификаторов наблюдается положительное увеличение каждой из метрик (табл. 1). При этом прирост F1-score сильно зависит от используемой модели и первоначальных показателей качества классификации. Так, все модели глубокого обучения, а также SVC и RF получили прирост менее 1 % в показателях F1-score. В то же время классификаторы, которые показали изначальный результат хуже, получили значительный прирост в данной метрике. Так, улучшение качества классификации для методов k-NN и DTree составило 2,04 % и 3,27 % соответственно. Для моделей LSVC, LR, LDA, SVC-SGD и NB оно составило от 6,22 % до 9,15 %. Наиболее заметный положительный эффект применения алгоритма улучшения классификации получен с использованием классификатора Perceptron, что позволило увеличить рассматриваемую метрику на 11,84%.

Существенный прирост наблюдается в показателе Graph-score после применения алгоритма улучшения качества классификации. Среди моделей искусственных нейронных сетей наибольший прирост в точности получили модели U-Net и FCNN (+77,78% и +72,22% соответственно), а наименьший – модель ResNet-101 (+11,12%). Модели машинного обучения k-NN, DTree, LSVC, LR, LDA, SVC-SGD, Perceptron и NB показывали 0% корректно размеченных объектов, однако применение алгоритма улучшения классификации позволило заметно увеличить качество разметки на величину от 55,56% до 100%. Итого пять методов разметили верно 100% валидационного набора данных: FCNN, U-Net, ResNet-50, RF и NB. Необходимо также отметить, что среди указанных методов ResNet-50 показал наивысший результат Graph-score до применения алгоритма улучшения классификации (см. таб. 1). Еще три метода добились значения метрики выше 90%, они включают в себя ResNet-18, SVC и SVC-SGD.

Табл. 1. Метрики качества обученных моделей на валидационной выборке до и после применения алгоритма улучшения классификации GraphAlg

Модель	F1-score до GraphAlg (%)	F1-score после GraphAlg (%)	Δ F1-score (%)	Graph-score до GraphAlg (%)	Graph-score после GraphAlg (%)	Δ Graph-score (%)
ResNet-16	91,55	91,77	0,22	27,78	72,22	44,44
ResNet-18	91,77	91,91	0,14	27,78	94,44	66,66
ResNet-34	92,14	92,53	0,39	27,78	72,22	44,44
ResNet-50	91,08	91,23	0,15	55,56	100	44,44
ResNet-101	92,38	92,55	0,17	44,44	55,56	11,12
ResNet-152	90,94	91,18	0,24	44,44	83,33	38,89
FCNN	91,66	92,04	0,38	27,78	100	72,22
U-Net	91,61	91,97	0,36	22,22	100	77,78
SVC	90,28	90,42	0,14	44,44	94,44	50
RF	89,98	90,1	0,12	27,78	100	72,22
k-NN	85,81	87,85	2,04	0	72,22	72,22
DTree	85,58	88,85	3,27	0	88,89	88,89
LSVC	83,05	89,35	6,3	0	88,89	88,89
LR	82,52	88,74	6,22	0	88,89	88,89
LDA	80,24	88,58	8,34	0	88,89	88,89
SVC-SGD	80,17	88,79	8,62	0	94,44	94,44
Perceptron	78,29	90,13	11,84	0	55,56	55,56
NB	72,14	81,29	9,15	0	100	100

Полужирным шрифтом выделены наилучшие результаты в столбце. Минимум и максимум значений других метрик среди указанных моделей: до применения GraphAlg – accuracy [76,01; 95,74] %, precision [80,01; 95,01] %, recall [72,94; 90,97] %. После применения GraphAlg – accuracy [85,18; 95,92] %, precision [88,36; 95,39] %, recall [83,42; 91,11] %.

Как видно из табл. 1, несмотря на то, что модель NB достигла 100% Graph-score, метрика F1-score выделяет её как наименее эффективную. Рис. 3 показывает результат применения алгоритма Graph-Alg к предсказаниям моделей NB и FCNN. Заметно, что до применения алгоритма модель NB наибольшую часть эндо ПЖ (синий цвет) помечала как эпи (зеленый цвет), помимо этого, неверно размеченные крупные области можно встретить на эндо ЛЖ (красный цвет). Напротив, при применении метода FCNN неправильно размеченными оказываются лишь небольшие области полигональной сетки желудочков, включающие в себя в среднем 4–5 точек. Применение алгоритма улучшения классификации в обоих случаях позволило избавиться от большинства неправильно классифицированных областей полигональной сетки (см. рис. 3). Отметим также, что результаты других моделей с высоким F1-score визуально отличаются незначительно от FCNNН, поэтому мы не приводим дополнительные рисунки. Несомненно, величина прироста рассматриваемых метрик связана с величиной областей на полигональных сетках, которые изначально классифицировались неверно, но после применения алгоритма улучшения классификации соответствовали нужному классу. В частности, модель FCNN получила небольшую прибавку в значении метрики F1-score (0,38%), в то время как результат работы NB улучшился на 9,15%.

Алгоритм улучшения классификации позволил сделать ряд рассматриваемых моделей пригодными для построения бивентрикулярной координатной системы. Полученные результаты (табл. 1) подтверждают, что алгоритм улучшения классификации является эффективным инструментом в контексте решаемой задачи.

Беря во внимание обе метрики Graph-score и F1-score, наиболее предпочтительными классификаторами оказались FCNN, U-Net, ResNet-50, RF, ResNet-18, SVC, SVC-SCD.

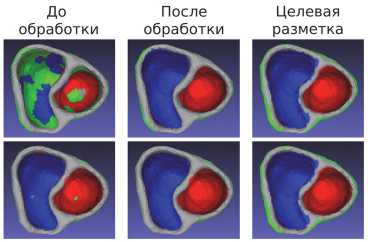
Рис. 3. Результат применения постобработки к поверхностной сетке сердца, сегментированной с помощью модели NB (верхний ряд) и FCNN (нижний ряд). Синим и красным отмечен эндо правого и левого желудочков соответственно, зеленым выделен эпи, серым выделено основание желудочков

Как описано выше, нейронные сети показали сопоставимые результаты, несмотря на большую разницу в количестве используемых обучаемых параметров. Также необходимо отметить, что ни одна из использованных моделей не получила показатель accuracy выше 96% и recall выше 91 %. При дальнейшем изучении данного вопроса выявлено, что низкий показатель recall получен из-за класса, соответствующего основанию желудочков. Нет четких критериев определения границ оснований желудочков, и медицинский эксперт ставит их в некоторой степени произвольно. Вероятно, в связи с этим модели не способны научиться в точности воспроизводить экспертную разметку. Пример таких ошибок можно увидеть на рис. 3.

На тестовой выборке почти все модели показали F1-score около 90 % (86 % – 91 %), кроме SVC-SGD (70 %). После применения GraphAlg качество SVC-SGD выросло до 87 %, а у остальных моделей выросло незначительно (не более, чем на 3 %). Тестовый Graph-score до применения GraphAlg у всех моделей низкий, с максимальным значением 25 % для модели RF. По значениям Graph-score после применения GraphAlg можно выделить три наилучшие модели: U-Net, SVC-SGD и RF, c Graph-score 95 %, 90 % и 85 % соответственно. У остальных моделей значение этой метрики не превышает 75 %, а снижение по сравнению со значением на валидаци-онной выборке составило больше 24 %.

Табл. 2. Метрики качества обученных моделей на тестовой выборке до и после применения алгоритма улучшения классификации GraphAlg

Модель	F1-score до GraphAlg (%)	F1-score после GraphAlg (%)	Δ F1-score (%)	Graph-score до GraphAlg (%)	Graph-score после GraphAlg (%)	Δ Graph-score (%)
U-Net	89,56	91,52	1,96	15,00	95,00	80,00
SVC-SGD	70,10	87,35	17,25	0,00	90,00	90,00
RF	90,98	91,38	0,40	25,00	85,00	60,00
ResNet-50	86,25	89,74	3,49	5,00	75,00	70,00
SVC	90,40	91,79	1,39	15,00	70,00	55,00
ResNet-18	87,73	89,77	2,04	20,00	70,00	50,00
FCNN	88,26	90,40	2,14	10,00	65,00	55,00

Полужирным шрифтом выделены наилучшие результаты в столбце. Минимум и максимум значений других метрик среди указанных моделей: до применения GraphAlg – accuracy [70,31; 94,85] %, precision [72,88; 94,56] %, recall [69,95; 89,76] %. После применения GraphAlg – accuracy [89,53; 95,59] %, precision [89,94; 95,19] %, recall [86,05; 90,58] %.

Табл. 3. Производительность классификаторов

Модель	Время на CPU, с	Время GPU, с
ResNet-16	0,3682	0,0174
ResNet-18	0,412	0,0314
ResNet-34	0,5812	0,0395
ResNet-50	1,3053	0,0665
ResNet-101	1,5197	0,1053
ResNet-152	1,8343	0,1481
FCNN	0,046	0,0026
U-Net	143,3201	0,6458
SVC	26,8897
RF	0,0139
k-NN	2,9119
DTree	0,0012
LSVC	0,0072
LR	0,0073
LDA	0,006
SVC-SGD	0,0061
Perceptron	0,0061
NB	0,0707

Полужирным курсивом отмечены классификаторы, отобранные по метрикам F1-score и Graph-score. CPU – центральный процессор, GPU – графический ускоритель

С практической точки зрения выбираемая классификационная модель должна иметь низкие требования к вычислительным мощностям, а также быть быстрой и точной. Табл. 3 показывает среднее время, затраченное на обработку 1000 точек из клинических данных, на основании 100 проведенных экспериментов для каждой обученной модели. Все методы машинного обучения были протестированы с использованием процессора Intel Core i5-12500h, дополнительно для каждой нейронной сети были проведены эксперименты с применением графического ускорителя NVIDIA RTX 3060m. Наиболее эффективными с точки зрения временной производительности оказались модели DTree, FCNN с использованием графического ускорителя, LDA, Perceptron, SVC-SGD, LSVC и LR, которым потребовалось менее 0,01 с для обработки 1000 точек полигональной сетки. Наименее быстрыми оказались модели глубокого обучения, запускаемые без использования графического ускорителя, а также k-NN и SVC.

Подводя итог, можно выделить модель U-Net как наиболее подходящую в контексте практического применения с использованием графического ускорителя. Модель U-net требует менее 1 секунды на классификацию 1000 точек трехмерного объекта и показывает наилучшие результаты классификации среди всех протестированных моделей. При отсутствии доступа к графическому ускорителю рекомендуется использовать модели RF и SVC-SGD, так как данные модели требуют менее 0,014 с на обработку такого же количества точек и показывают сопоставимые с U-Net показатели F1-score и Graph-score.

Проведенное исследование имеет ряд ограничений, которые будут устранены в дальнейших работах. Во-первых, графовый алгоритм улучшения результатов классификации нуждается в более глубоком анализе. В текущем виде он представлен в качестве эвристического алгоритма, который демонстрирует эффективность эмпирически. Возможна теоретическая оценка эффективности алгоритма при выполнении определенных условий. В дальнейшем возможно перечислить все возможные ошибки, совершаемые классификаторами, с точки зрения компонент связности различных классов. На основе этого анализа ошибок можно сформулировать условия на результатах классификации, при которых применение алгоритма гарантированно приводит к выполнению условий GraphTest, а также предложить более совершенный алгоритм. Во-вторых, важно провести сравнение предложенного подхода с другими имеющимися в литературе. Формулировок, в точности соответствующих нашей, мы не нашли, но возможно воспроизвести работы, решающие близкие задачи, и оценить качество методов на наших данных и тестах. В-третьих, для задачи построения координатной системы на желудочках сердца интерес представляет определение положения верхушки левого желудочка, эта задача также может быть рассмотрена, например, как добавление пятого класса в задачу классификации.

Заключение

Проведено сравнение моделей машинного обучения (нейронные сети с архитектурами FCNN, U-Net, ResNet и классификаторы, содержащиеся в пакете scikit-learn) для задачи классификации поверхностей желудочков сердца. В ходе исследования предложена метрика для оценки качества классификации с точки зрения построения бивентрикулярной координатной системы. Предложен детерминированный графовый алгоритм для исправления потенциальных ошибок классификации. Установлено, что предложенный алгоритм оказался эффективным инструментом для минимизации ошибок, допускаемых моделями машинного обучения в ходе классификации. Среди исследованных моделей наиболее эффективной для решения поставленной задачи оказалась модель U-Net. С точки зрения практической применимости также необходимо отметить модели RF и SVC-SGD, так как они не нуждаются в использовании дорогих вычислительных мощностей и графических ускорителей, предоставляя сопоставимую точность классификации и быструю скорость работы.

Исследование выполнено при финансовой поддержке Министерства науки и высшего образования Российской Федерации в рамках Программы развития Уральского федерального университета имени первого Президента России Б.Н. Ельцина в соответствии с программой стратегического академического лидерства «Приоритет-2030».