Классификация поверхностных дефектов основного металла трубопроводов по результатам комплексной диагностики

Сегодня в Российской Федерации существует и продолжает сооружаться большое количество объектов трубопроводного транспорта. Анализ материалов [1 –4] показывает, что на этих объектах среди эксплуатационных дефектов наибольшую часть составляют поверхностные коррозионные повреждения, возникающие под воздействием внешней среды. Такие дефекты можно разделить на плоскостные, например, стресс-коррозионные трещины, и объемные – местная коррозия (питинги, свищи и т.д.) [5]. Для обеспечения длительной безопасной эксплуатации оборудования, трубопроводов, других сооружений в настоящее время актуально развитие технологий диагностирования с применением комплекса методов неразрушающего контроля (НК), позволяющих производить классификацию данных дефектов в автоматическом режиме.

Для выявления поверхностных эксплуатационных дефектов трубопроводов применяют ряд физических методов НК, таких как вихретоковый (ВК) и ультразвуковой (УК) [6]. При этом возникает вопрос, может ли комплекс нескольких методов НК дать более надежные и достоверные результаты, чем каждый метод, применяемый по отдельности. С точки зрения based on complex diagnostics results. Computer 6179-CO-1185.

логики применение большего количества информации в процессе принятия решения приводит к принятию наиболее правильного решения. В данном случае по результатам работы комплекса методов НК происходит принятие решения о типе выявленного поверхностного дефекта, таком как плоскостной или объемный дефект, т.е. комплекс методов НК решает задачу классификации типов поверхностных дефектов.

Системы, которые позволяют производить классификацию данных неразрушающего контроля, называются классификаторами, которые основываются на двух основных подходах: статистические методы и методы на основе искусственного интеллекта (ИИ). Основными методами ИИ являются классификаторы на основе нечеткой логики [7], метода опорных векторов [8], деревьев решений [9], нейронных сетей [10] и т.д. Основными статистическими методами являются Байесовский вывод и теория Демпстера–Шафера [11]. Теория Демпстера–Шафера является обобщением частного случая теоремы Байеса, учитывающим вероятности составных гипотез как объединения множества независимых гипотез.

Модели объединения данных на основе статистических методов широко применяются в науке и технике [12]. Специализированные методы принятия решений на основе составных (а иногда и противоречивых) входных данных называют «слиянием данных» [13]. Сегодня принципы слияния данных уже применялись к задачам неразрушающего контроля в работах [14– 17]. В данной работе разрабатываются модели слияния данных УК и ВК на основе Байесовского вывода и теории Демпстера–Шафера для решения задачи классификации типов поверхностных эксплуатационных дефектов основного металла трубопроводов и рассматривается их работоспособность. Данные типы дефектов имеют различные степени опасности: трещины имеют высокую опасность, т.к. они имеют тенденцию к росту при циклических нагрузках, язвенная коррозия имеет низкую степень опасности, поэтому при диагностике её целесообразно классифицировать в автоматическом режиме. В работах [18, 19] показано, что только по результатам УК не удается произвести классификацию дефектов, поэтому необходимы модели совместной обработки данных результатов УК и ВК, которые не были найдены при анализе литературных данных.

1.    Методика проведения исследований

Для исследования возможностей классификации поверхностных эксплуатационных дефектов основного металла трубопроводов был изготовлен ряд образцов, содержащих имитаторы поверхностных дефектов. Плоскостные поверхностные дефекты (трещины, коррозионное растрескивание под напряжением) имитировались поверхностными пазами, выполненными электроэрозионным способом, а объемные поверхностные дефекты (язвенная, питтинговая коррозия) – вертикальными сверлениями.

Данные образцы, как это показано в [18, 19], содержали сверления глубиной 5 мм и диаметрами 1; 1,5; 2; 2,5; 3; 3,5; 4; 4,5; 5; 7; 8,5; 10 мм; сверления диаметром 3 мм и глубинами 0,25; 0,4; 0,5; 0,75; 1,0; 1,2; 1,5; 2,0; 2,5; 3,0; 3,5; 4,0; 4,5; 5,0 мм; пазы раскрытием 0,15 мм и глубинами 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,75; 1,0; 1,5; 2,0; 2,5; 3,0; 4,0 мм; пазы глубиной 0,5 мм и раскрытиями 0,15; 0,25; 0,5; 0,75; 1,0; 1,5 мм; пазы раскрытием 0,15 мм, глубиной 0,5 мм и углами наклона к поверхности образца 15°; 30°; 45°; 60°; 75°; 90°. Фотографии отдельных образцов с вертикальными сверлениями и электроэрозионными пазами представлены на рис. 1.

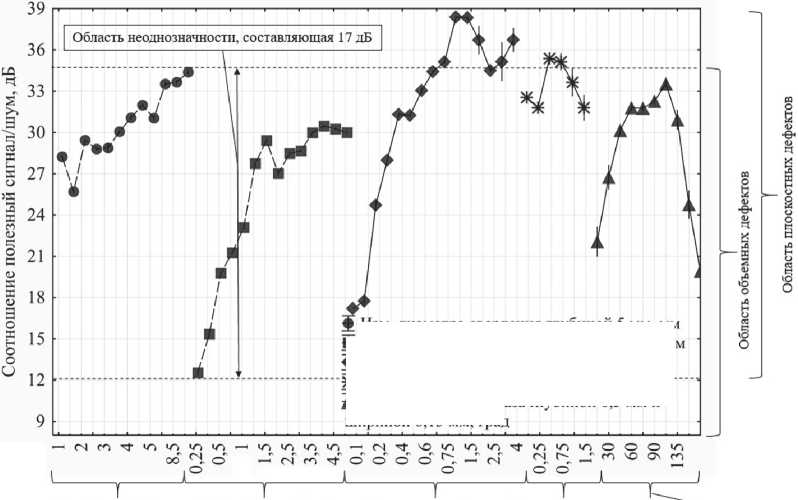
Ультразвуковые исследования выполнялись с использованием конфигурируемого блока дефектоскопической электроники Sonaflex [20], к которому был подключен бесконтактный электромагнитноакустический преобразователь (ЭМАП), излучающий Рэлеевские волны с центральной частотой 1 МГц. В качестве параметра, измеряемого при ультразвуковом контроле, выступала максимальная амплитуда эхо-сигнала, отраженного от дефекта. В данном случае время прихода эхо-сигнала, отраженного от поверхностного дефекта, не несет полезной информации, т.к. анализируется временная область, находящаяся в непосредственной близости от зондирующего импульса. Таким образом, классификация дефектов по типам (объемный или плоскостной) в случае ультразвукового контроля может быть проведена только по одному параметру – амплитуде ультразвукового эхо-сигнала (соотношение полезный сигнал /шум). Для оценки возможности классификации дефектов только по результатам ультразвукового контроля необходимо сопоставить значения амплитуд, полученных от сверлений и пазов различных размеров. Для этого все результаты измерений из [18, 19] были нанесены на график, который представлен на рис. 2.

б)

а)

Рис. 1. Фото образцов с поверхностными дефектами: а) электроэрозионными пазами, б) вертикальными

сверлениями

Как видно из рис. 2, первые две кривые слева принадлежат данным, полученным от вертикальных сверлений (имитаторов объемных дефектов), а оставшиеся три кривые – данным от пазов (имитаторов плоскостных дефектов). При этом несмотря на то, что амплитуды сигналов от пазов, в целом, выше амплитуд сигналов от сверлений, области амплитудных значений для них перекрывают друг друга приблизительно на 17 дБ. Таким образом, с учетом указанной зоны перекрытия невозможно однозначно классифицировать тип дефекта по амплитуде ультразвукового сигнала, следовательно, для успешной классификации типов поверхностных дефектов необходимо комбинировать УК с другими методами контроля.

Одним из основных методов НК, позволяющих выявлять поверхностные эксплуатационные дефекты, результаты которого можно комбинировать с УК, является вихретоковый метод. ВК осуществляется с применением различных типов вихретоковых преобразователей (ВТП), которые классифицируются по типу преобразования параметров объекта контроля в выходной сигнал на параметрические и трансформаторные, а также по способу получения информации об объекте контроля на абсолютные и дифференциальные [21]. В параметрических ВТП для возбуждения и измерения используется одна катушка, а в трансформаторных – не менее двух. Параметрические

ВТП более просты в изготовлении, но трансформаторные ВТП более устойчивы к влияниям внешних факторов. В абсолютных ВТП обычно используется одна измерительная обмотка, абсолютные значения сигнала которой считываются при измерениях. В дифференциальных ВТП используются две измерительные катушки, и при измерениях считывается разница между значениями сигналов от них. Дифференциальные ВТП более устойчивы к изменению зазора и других внешних факторов [22].

3 мм, мм мм, мм

0,15 мм,0

мм, мм

Рис. 2. Обобщенные результаты всех ультразвуковых измерений [19]

I Ьменение диаметра I Гзменение глубины сверления глубиной 5 сверления диаметром

Изменение ширины Изменение угла наклона паза паза глубиной 0,5 глубиной 0,5 мм и шириной

Изменение глубины паза шириной 0,15 мм, мм

Изм. диаметра сверления глубиной 5 мм, мм ( Изм. глубины сверления диаметром 3 мм, мг $ Изм. глубины паза шириной 0,15 мм, мм 8 Изм.тпргтыпаза глубиной"0,5 мм,'Мм 1 Изм. угла наклона паза глубиной 0,5 мм и шириной 0,15 мм, град

2.    Выбор вихретокового преобразователя

Так как существует 4 основных типа ВТП: параметрический абсолютный (ПА), параметрический дифференциальный (ПД), трансформаторный абсолютный (ТА) и трансформаторный дифференциальный (ТД) – в данной работе определялся оптимальный ВТП, наилучшим образом подходящий для определения типов поверхностных дефектов (плоскостные и объемные). Вихретоковые измерения производились с применением четырех ВТП карандашного типа фирмы Olympus, характеристики которых представлены в табл. 1.

Табл. 1. Параметры используемых ВТП

№	Тип ВТП	Шифр	Диапазон рабочих частот
1	Параметрический абсолютный	U8623152	100 кГц –500 кГц
2	Параметрический дифференциальный	U8623150	500 кГц –2 МГц
3	Трансформаторный абсолютный	U8623170	100 кГц – 1 МГц
4	Трансформаторный дифференциальный	U8623173	500 кГц –3 МГц

При вихретоковом контроле сигнал от дефекта отображается на комплексной плоскости, при этом измеряется не только амплитуда, а также и фаза регистрируемого сигнала. По результатам вихретоковых измерений, проведенных на изготовленных образцах с поверхностными дефектами, были получены значения амплитуды и фазы вихретоковых сигналов от искусственных дефектов на образцах для каждого из четырех ВТП. На основе проведенных измерений была сформирована выборка, представляемая в виде таблицы, содержащей 9 столбцов, а именно значение амплитуды и фазы вихретокого сигнала для каждого из четырех ВТП и 9-й столбец – тип дефекта: объемный или плоскостной. Всего было произведено 269 измерений.

Для выбора ВТП, оптимального для классификации поверхностных дефектов, оценивалось: какие амплитуда и фаза сигнала рассматриваемых ВТП из данной выборки имеют наибольшие идентификационные признаки для классификации поверхностных дефектов с использованием дисперсионного анализа (ANOVA) и отбора признаков с применением алгоритма «экстра деревья» (Extra Trees Classifier). В дисперсионном анализе (ANOVA) вычисляются значения коэффициента Фишера для имеющихся параметров (в нашем случае это амплитуда и фаза различных ВТП), и за оптимальные принимаются параметры с максимальными значениями коэффициента Фишера [23]. Помимо этого, на исследуемой выборке проводился отбор признаков с применением алгоритма «экстра деревья» (Extra Trees Classifier), где определялся параметр степени влияния на возможность классификации дефектов амплитуд и фаз сигналов, полученных ВТП различного типа. Результаты от- бора признаков для выбора оптимального ВТП представлены в табл. 2.

Табл. 2. Результаты отбора признаков для выбора оптимального ВТП

Тип ВТП	Параметр сигнала	Коэффициент Фишера (ANOVA)	Параметр степени влияния (Extra Trees Classifier)
Параметрический	Амплитуда	657,7	0,146
абсолютный	Фаза	245,7	0,059
Параметрический	Амплитуда	452,2	0,051
дифференциальный	Фаза	1052,5	0,12
Трансформаторный	Амплитуда	442,3	0,078
абсолютный	Фаза	1073,2	0,155
Трансформаторный	Амплитуда	534,3	0,159
дифференциальный	Фаза	759,3	0,129

Как видно из табл. 2, если суммарно оценивать значения критериев для амплитуды и фазы определенного типа ВТП, то наибольшие значения имеют: трансформаторный абсолютный по критерию Фишера и трансформаторный дифференциальный ВТП по параметру степени влияния. В итоге был выбран трансформаторный дифференциальный ВТП, т.к. он имеет меньшую чувствительность к зазору и другим внешним факторам.

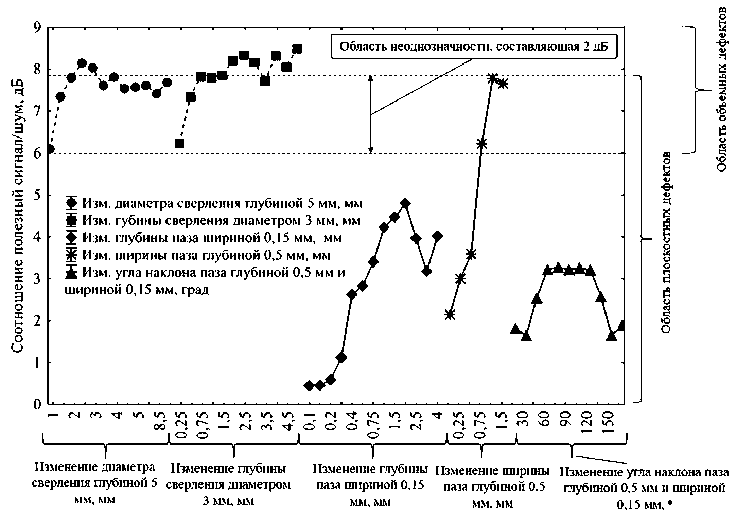
Для определения возможности классификации плоскостных и объемных поверхностных дефектов ВК по отдельности все результаты измерений с использованием трансформаторного ВТП были нанесены на графики, которые представлены на рис. 6.

а)

б)

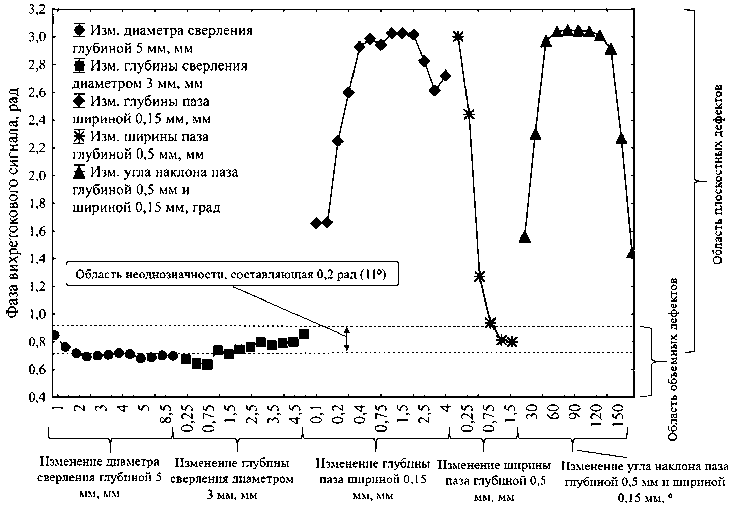
Рис. 3. Обобщенные результаты по всем вихретоковым измерениям для значений амплитуды – а) и фазы – б)

Как видно из рис. 3 а и 3 б , первые две кривые слева принадлежат данным, полученным от вертикальных сверлений (имитаторов объемных дефектов), а оставшиеся три кривые – данным от пазов (имитаторов плоскостных дефектов). При этом как для значений амплитуды, так и для значений фазы присутствуют зоны перекрытия значений, получаемых от объемных и плоскостных дефектов на 2 дБ и 0,2 рад (11⁰) соответственно. При ВК неоднозначность по определению типа дефекта значительно меньше, чем при УК, но при ВК значительно выше вероятность появления ложных сигналов, связанная с тем, что при изменении зазора между ВТП и объектом контроля на комплексной плоскости возникает кривая отрыва по фазе, близкой к сигналу от объемного дефекта, изменения относительной магнитной проницаемости ферромагнитного материала на комплексной плоскости отображаются по фазе, близкой к сигналу от поверхностного дефекта. Примеры данных ложных сигналов при ВТП представлены в работе [24]. Таким образом, с учетом указанных зон перекрытия и наличия ложных сигналов при ВК невозможно однозначно классифицировать тип дефекта по амплитуде и фазе, и для успешной классификации необходимо комбинировать ВК с другими методами контроля.

3.    Подготовка данных

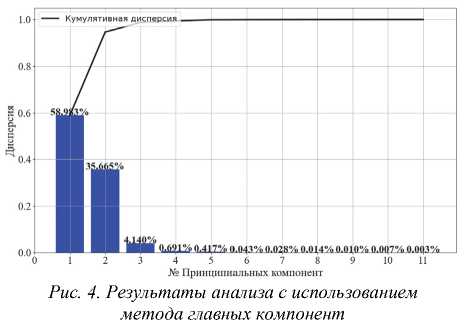
В результате ультразвукового и вихретокового контроля на образцах с плоскостными и объемными дефектами была сформирована выборка, представляемая в виде таблицы, содержащей 10 столбцов, а именно: амплитуда ультразвукового сигнала для ЭМАП, амплитуды и фазы вихретокого сигнала для каждого из четырех ВТП и 10-й столбец – тип дефекта: объемный или плоскостной. Помимо того, что был выбран оптимальный ВТП, для данной выборки был произведен анализ с использованием метода главных компонент (PCA). Метод главных компонент (PCA) представляет собой ортогональное линейное преобразование, которое отображает данные из исходного пространства признаков в новое пространство меньшей размерности. При этом первая ось новой системы координат строится таким образом, чтобы дисперсия данных вдоль неё была бы максимальна. Вторая ось строится ортогонально первой так, чтобы дисперсия данных вдоль неё была бы максимальной из оставшихся возможных и т.д. В новом пространстве признаков меньшей размерности дисперсия между осями будет перераспределена так, чтобы максимизировать дисперсию по каждой из них [25]. Результаты анализа с применением метода главных компонент (PCA) показаны на рис. 4.

Как видно из рис. 4, основная дисперсия (98,8 %) содержится в первых трех принципиальных компонентах, т.е. исходное пространство можно разложить в базисе трех принципиальных компонент без существенной потери дисперсии.

В случае совместного анализа данных УК и ВК имеется три числовых входных параметра, а именно амплитуда, полученная при УК; амплитуда, полученная при ВК, и фаза, полученная при ВК. На рис. 5 представлено распределение полученных при измерениях данных в пространстве трех указанных параметров.

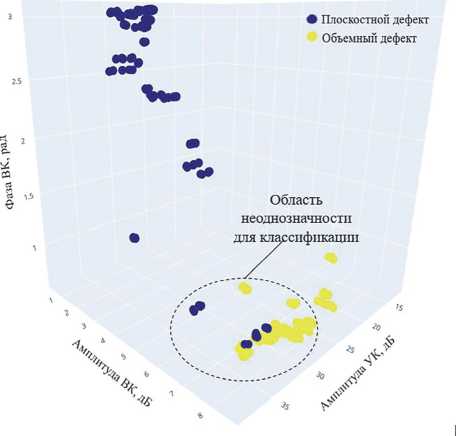
Рис. 5. Входные параметры при совместном анализе данных УК и ВК для классификации поверхностных дефектов

Как видно из рис. 2,3,5, не удается однозначно интерпретировать тип эксплуатационного поверхностного дефекта (объемный или плоскостной) по трем параметрам, а именно: амплитуда, полученная при УК; амплитуда, полученная при ВК, и фаза, полученная при ВК, поэтому необходимы модели на основе статистических методов, таких как Байесовский вывод и теория Демпстера–Шафера.

4.    Описание моделей классификации

При построении модели классификации на основе Байесовского вывода были установлены следующие гипотезы: данные принадлежат классу «Плоскостной дефект»: {П}; данные принадлежат классу «Объем- ный дефект»: {О}. Принятие решения о принадлежности данных к определенному классу (гипотезе) происходит по максимальному значению вероятности принадлежности к классу в случае заданных параметров неразрушающего контроля, которая вычисляется по формуле Байеса [11]:

P ( hi\ S УК , S ВК.а , S ВК.ф ) —

P ( S УК , S ВК.а , S ВК.ф I h i ) ' P ( h i ) P ( S УК , S ВК.а , S ВК.ф )

где h i – гипотеза, которая принимает значения {П} или {О};

S УК , S BK.а , S BK.ф – измеренные значения параметров неразрушающего контроля, а именно амплитуда, полученная при УК; амплитуда, полученная при ВК, и фаза, полученная при ВК соответственно.

P ( S УК , S BK.а , S BK.ф | h i ) – вероятность получения значений параметров неразрушающего контроля при известном типе дефекта. Так как Байесовский вывод подразумевает независимость распределений случайных величин всех параметров, то P ( S УК , S BK.а , S BK.ф | h i ) может быть вычислена как произведение вероятностей P ( S j | h i ), которые, в свою очередь, вычисляются как правдоподобия нормального распределения с параметрами математического ожидания и среднеквадратичного отклонения, вычисляемых по обучающим выборкам для каждого параметра и каждого типа дефектов.

Вычисление знаменателя P ( S УК , S BK.а , S BK.ф ) в формуле (1) опускается, т.к. он будет одинаковым для обеих гипотез и не несет дополнительной информации для сравнения вероятностей их появления при известных параметрах неразрушающего контроля.

P ( h i ) – априорная вероятность принадлежности данных к определенному типу дефекта, которая вычисляется по обучающей выборке для обеих гипотез как отношение количества всех измерений, принадлежащих к определенному типу, к общему количеству измерений.

При построении модели классификации на основе теории Демпстера–Шафера были установлены следующие предположения: П – плоскостной дефект, О – объемный дефект. На основе данных предположений была построена система распознания 9 = {{П},{О}}. Согласно теории Демпстера-Шафера, гипотезами в модели классификации являются подмножества системы распознания [26], а именно 2 ⁹ ={ 0 , {П}, {О}, {ПилиО}}.

Согласно теории Демпстера–Шафера каждому подмножеству системы распознания присваиваются массы m ( ■ ), удовлетворяющие следующим свойствам:

m : 2" >  [ 0,1 ] ; m ( 0 ) — 0; S m ( X ) — 1. (2)

X С0

В разработанной модели присвоение масс происходило следующим образом: на обучающей выборке были определены диапазоны максимальных и минимальных значений параметров амплитуды УК, амплитуды ВК и фазы ВК для объемных и плоскостных дефектов. После чего производилось определение, к какой гипотезе относятся данные, следующим образом: если значение параметра НК X находится в диапазоне min({П})

Далее производилось присвоение численных значений масс для каждой гипотезы следующим образом: если данные принадлежат к одному классу {О}/{П}, то массовые вероятности принимаются равными mi ({П}) = mi ({О}) = 0,4, mi ({П или О}) =0,6 (данные значения определены экспериментально, при которых классификатор работает наилучшим образом согласно коэффициенту Жаккара и F1-мере). Если данные принадлежат к обоим классам ({П или О}), то массовая вероятность принимается равной mi ({П или О})= 1. Если данные не принадлежат никакому классу, то массовая вероятность принимается равной mi({0}) = 0. Общая схема присвоения масс представлена на рис. 6.

maz({0})

L {0}

тах({П})

min({0})

- [П или 0}

min({n})

- Ш)

т;({П}) = т;({0}) = 0.4

т, ({П или 0}) = 0.6

—►mj({n или О}) = 1 т;({П}) = т;({0}) = 0.4 т,({П или 0}) = 0.6

Рис. 6. Схема присвоения масс

Далее выполнялось вычисление итоговых масс по правилу комбинирования данных Демпстера [27] согласно (3).

SXinXj— Zm^{( X)}m 2 ⁽Xj) m^{( )—}1 -SXnXj—0mi(X.)m2(Xj)

Принятие гипотез осуществлялось по следующему принципу:

– Если максимальную массу имеют гипотезы, не учитывающие неоднозначность, а именно {П} или {О}, то принимается та гипотеза, у которой больше функция доверия Bel (X) (в данном случае она совпадает с массой), которая определяется следующим образом [26]:

Bel :2® ^[0,1]; Bel(X)— S m(X).

XiC X

– Если максимальную массу имеет гипотеза с неоднозначностью, а именно {П или О}, то рассчитывается значение функции FSV по формуле (4).

sd^({П})х sd^({O^}) sd ({П и О})   ,

где sd (■) - среднеквадратическое отклонение.

После чего выбирается параметр a с наименьшим значением функции FSV и вычисляется модуль разности dj между значением a и средним значением ā для всех гипотез, по формуле (5).

dj = |a_y -j.                                     (5)

В итоге принимается гипотеза с наименьшим значением d.

5.    Оценка работоспособности моделей

Для обучения и проверки работоспособности моделей классификации применялась кросс-валидация, при которой производились 4 итерации, где все данные, полученные при измерениях, были разделены на 5 различных обучающих и тестовых выборок, составивших 215 и 54 элемента соответственно. Работоспособность моделей классификации определялась по средним арифметическим для всех итераций кросс-валидации таких метрик, как коэффициент Жаккара и F1-мера.

Коэффициент Жаккара является бинарной мерой сходства и вычисляется по формуле (6) [27].

У^пy

J (У, У )=-----q>                                   ⁽⁶⁾

У ^ y где | у п у | - количество результатов, принадлежащих к обоим множествам, | у и у | - общее количество результатов.

Коэффициент Жаккара не учитывает ошибки первого и второго рода (ложноположительное и ложноотрицательное соответственно), поэтому, помимо коэффициента Жаккара, вычислялись точность (precision), полнота (recall) и F1-мера. Для их вычисления строится таблица контингентности (табл. 3).

Табл. 3. Таблица контингентности

Категория		Экспертная оценка
		Плоскостной	Объемный
Оценка модели	Плоскостной	истинноположительное (TP)	ложноположительное (FP)
	Объемный	ложноотрицательное (FN)	истинноотрицательное (TN)

Далее вычисляются значения точности и полноты по формулам (15), (16) [27]. Точность показывает долю результатов, которые модель правильно отнесла к выбранному классу относительно всех результатов, которые модель отнесла к этому классу. Полнота показывает долю результатов, которые модель отнесла к выбранному классу из всех результатов этого класса.

£ TP Precision = —----—---, £ TP + £ FP

Recall =

£ TP

£ TP + £ FN'

Значение F1-меры представляет собой совместную оценку точности и полноты и вычисляется по формуле (9) [27].

2 ■ Precision ■ Recall

F1 =----------------

Precision + Recall

Результаты тестирования моделей представлены в табл. 4.

Табл. 4. Результаты тестирования моделей

Модели на основе	Средний коэффициент Жаккара, %	Средняя точность (Precision), %	Средняя полнота (Recall), %	Средняя F1 – Мера, %
Байесовского вывода	96,1	96,08	96,47	96,05
теории Демпстера– Шафера	96,29	96,25	96,69	96,25

Как видно из табл. 3, модель, основанная на теории Демпстера–Шафера, показывает лучшие результаты, чем модель на основе Байесовского вывода, но в целом обе модели показали высокую достоверность (около 96 %) по всем применяемым метрикам.

Заключение

• 1.    С использованием дисперсионного анализа (ANOVA) и отбора признаков алгоритмом «экстра деревья» (Extra Trees Classifier) произведен выбор типа вихретокового преобразователя, оптимального для классификации поверхностных дефектов на типы – объемный и плоскостной. Показана неоднозначность классификации поверхностных дефектов по амплитуде ультразвукового и вихретокового сигнала, а также по фазе вихретоквого сигнала по отдельности, которая составляет 17 дБ, 2 дБ и 0,2 рад (11⁰) соответственно.

• 2.    Произведен анализ полученных данных с применением метода главных компонент (PCA), по результатам которого определено, что основная дисперсия (98,8 %) содержится в первых трех принципиальных компонентах.

• 3.    Построены модели классификации поверхностных дефектов по типам (объемный и плоскостной) на основе статистических методов, таких как Байесовский вывод и теория Демпстера–Шафера. Для обучения и проверки работоспособности построенных моделей классификации применялась кросс-валидация, при которой производились 4 итерации, где все данные, полученные при измерениях, были разделены на 5 различных обучающих и тестовых выборок, составивших 215 и 54 элемента соответственно. Работоспособность построенных моделей классификации определялась по средним арифметическим для всех итераций кросс-валидации таких метрик, как коэффициент Жаккара и F1-мера.

• 4.    Определено, что модель, основанная на теории Демпстера–Шафера, показывает лучшие результаты, чем модель на основе Байесовского вывода, но в це-

• лом обе модели показали высокую достоверность (около 96%) по всем применяемым метрикам.

Исследование выполнено за счет гранта Российского научного фонда № 22-29-00524,