Классификация пространственно-временных краевых катастроф и равномерные асимптотические решения волновых уравнений, описывающих распространение волн в ионосферной плазме

ВЕСТНИК 2016

В1работе2исследовано применение теории краевых катастроф к проблеме описания распространения электромагнитного излучения в холодной плазме в нестационарном случае. Рас-смотрим3условия образования краевых особенностей при распространении частотно-модули-рованного радиоимпульса в однородной диспергирующей среде – ионосферной плазме. Как ωp обозначим плазменную частоту. Поместим ис- точник излучения в начало координат. Решение задачи может быть представлено в виде (см., например, [1–4]):

1     ^ :/ u (r,t) =— j j Z (ю) u0 (t) ^

^π -∞ -∞

точки зрения теории катастроф ответственна за пространственно-временную каустическую фокусировку геометрооптических лучей, а с физической точки зрения характеризует компрессию и декомпрессию радиосигнала. Приведем вторые производные фазовой функции Ф по τ и ω :

^exp i a

d a d i ,

∂ ² Φ

-- 2- = ^ф_п = ^ 0 ^f , ( ^т ) = 0 ,

где с - скорость света; r = ( x , y , z ) ; r =

£ ( ю ) = 1-- 2

ю

;

а ² ф

----=ф дг дю

- 1 * 0,

– эффективная диэлектрическая проницаемость среды (холодной плазмы);

д Ф          r top-

—^- = ^ф22 =-- ( (£ ^{( to}) )    ⁺ 5 2 ( ^to ) = ⁰. ⁽¹¹⁾

д toc

u

= u 0 ( n ) =

= — D ( n ) exp { i ® ( г + ^f ( ^т ) ) } ; r ₀

r0 ^ 0, Ю >> Юр, а функция Z(ю) = |Z(ю) |exp{is(ю

Можно показать, что

Ф ₁ k ₂ n = 0, n >  1, k >  1;

Ф 1 n = to o f_n ( t ) , n >  2.                         (12)

ВЕСТНИК 2016

– комплексная частотная характеристика фильтра приемного устройства. Рассмотрим полубес-конечный радиосигнал, для которого

D ⁽т ) = ^ ( Т ) A ^{( г} ) , ^ ( Т Н’ _г <  0,

a 0 - несущая частота; f ( г ) - гладкая функция, характеризующая частотную модуляцию радиосигнала, а A ( г ) - огибающая радиосигнала.

Значение интеграла определяется вкладами

В формулах (12) индексами обозначены соответствующие производные по τ (1) и по ω (2).

Из равенства (10) следует, что максимальный коранг матрицы Гесса вторых производных фазовой функции Ф равен 1. Поэтому здесь возможны лишь одномерные каспоидные (^ = A N ) фокусировки пространственно-временных геометрооптических лучей [3]. Если функция f ( т ) зависит от τ линейно, а s = 0, фокусировки пространственно-временных геометрооптических лучей не возникает. Когда

f ( ^г ) = ¹ а^г\ s = 0,                       ⁽¹³⁾

его критических точек, которые соответствуют лучевым семействам различного типа. Критическими точками интеграла (1) являются седловые точки фазовой функции, а также благодаря функции Хевисайда (см. (5)) – седловыми точками её сужения. Фазовая функция, определяющая совместно со своими сужениями лучевые семейства, которые описывают распространение радиосигналов в пространстве-времени, может быть представлена в виде:

ф ( г , ю , r, t ) = s ( ю ) + ю ^ t - г - -7 £Й ) ) +

+ ^0 (T + f (T)).(6)

Семейство пространственно-временных геометрооптических лучей находится как решение системы уравнений:

— = Ф1 = - Ю + to0 + to0 f1 (t) = 0,

∂τ дФ

— = Ф2 = t - г--^^ + s, (ю) = 0,(8)

дю 2 c^£(ю)   1 ( )

положение каустики в пространстве-времени ( r_c , t c ) как функции параметра т определяются равенствами:

cω r= = (£=) —c—; tc =г +- ato0top          c

rc

;

V ^£ с

где f j = d f / дг j , s j =d s / бю _j . Функция f ( г ) с

£ _с = £ ( ю _с ) ; ro c = го ₀ ( 1 + а т ) . (14)

Ранее в различных работах (см., например, в [5–9]) уже рассматривалась гладкая (без края) каустика пространственно-временных геометрооптических лучей.

На рис. 1 показаны каустика с краем (толстая линия), которая соответствует катастрофе B3, и пространственно-временные геометрооптические лучи (тонкие линии). Пространственновременные краевые лучи на рис. 1 не показаны.

В расчетах предполагалось, что круговая частота ω ₀ = 2π f ₀ , рабочая частота f ₀ = 13,5 МГц, круговая плазменная частота ω _p = 2π f _p, рабочая плазменная частота f _p ≈ 12,7 МГц.

При рассмотрении пространственно-временной фокусировки помимо вклада геометрооптических лучей существенную роль играет вклад

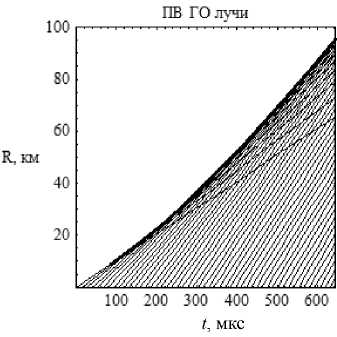
Рис. 1. Каустика с краем и пространственно-временные геометрооптические лучи a = 1500 c ^–1

пространственно-временных краевых лучей (см., например, [6; 8; 10]), порождаемых в данном случае начальной точкой полубесконечного радиоимпульса. Игнорировать вклад краевых лучей возможно, либо когда D( т ) плавная гладкая функция и краевые лучи отсутствуют, либо, с некоторой степенью точности, вдали от границы «свет-тень» пространственно-временных геометрооптических лучей, поскольку вклад краевых лучей обычно существенно меньше вклада геометрооптических лучей. Равномерный учет вклада краевых лучей был рассмотрен, например, в работах [11; 12]. Семейство краевых лучей может быть найдено из сужения функции Ф на начало радиоимпульса, то есть на границу τ = 0:

дФ

^ = 0 = t --+ s 1 = 0.                 (15)

дю      c ЕЕ

Нетрудно заметить, что при s 2 ( ю ) = 0 краевые лучи не фокусируются (поскольку ^ E = A 1 ). С точки зрения волновой теории катастроф, особенности, возникающие в окрестности границы «свет-тень», принадлежат серии B N +1 = (A N , A 1 ). Поэтому равномерная асимптотика выражается по формуле (см. [4; 13]):

u ( r, t ) =                                          (16)

^\     -        ( T^B - + 1 ^

= e* 1(I,)g 1"-■:л)+^(Ik)g |—1 + ( 11),1 к=2       ^ д лк-1 )         _ в которой (lj)g и (lj)E – геометрооптические и краевые коэффициенты асимптотического разложения, 0 - фаза бегущей волны, Xj - коэффициенты универсальной деформации, а

1 " N ^{+ 1}( л , ^ , л - ) =

+^

= J exp { i ( < N ⁺ 1 + X - Z + .„ + Л 1 С ) } d Z (17) – спец⁰иальная функция (СВК) краевой волновой катастрофы B _{N +1} (см. табл. 1).

На рис. 2 и 3 показаны трехмерная амплитудная структура СКВ (17) и линии равного уровня, соответственно, а на рис. 4 – фазовая структура.

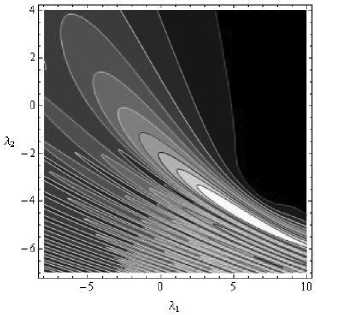
Рис. 3. Амплитуда СВК особенности B ₃, линии равного уровня

ВЕСТНИК 2016

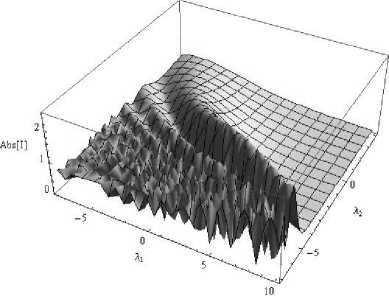
Рис. 2. Амплитуда СВК особенности B ₃ в формате 3D

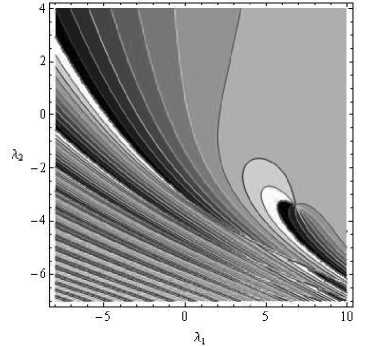
Рис. 4. Фаза СВК особенности B ₃, линии равного уровня

Если, наоборот, частотная модуляция отсутствует (f (т) = 0), а фазовая характеристика фильтра s (ю) не равна нулю, то может возникнуть фокусировка краевых лучей каспоидной серии. Так как пространственно-временные геометрооптические лучи не фокусируются, образуется краевая особенность CN+1 = (A1,AN) (см. табл. 1). Если 5 (to )= 2 a (to - to0 )2, уравнение каустики в параметрической форме (параметр ω) имеет вид [3]:

to 3/2

r = -ca—( e) , to to

p ^<  ω 0 ;

to - to ₀ + e— 7 , a <  0. to )

На рис. 5 показаны пространственно-временные краевые лучи в отсутствие влияния фильтра приемного устройства. Лучи выходят из точки, соответствующей началу радиоимпульса, и не образуют каустики. На рис. 6 показаны краевые лучи и их огибающая (каустика), когда фазовая характеристика фильтра не равна нулю. Пространственно-временные геометрооптические лучи на этих рисунках не показаны. Такой тип особенности является результатом взаимодействия сигнала с фильтром.

ВЕСТНИК 2016

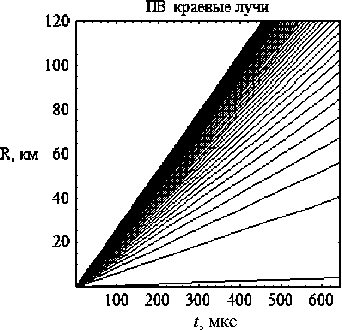
Рис. 5. Пространственно-временные краевые лучи, a = 0

ПВ краевые лучи

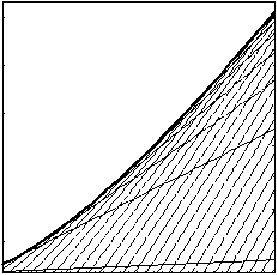
100 200 300 400 500 600

t , мкс

Рис. 6. Пространственно-временные краевые лучи, a = –1,4 10^–11 с ²

Равномерная асимптотика для этого случая имеет вид: [11] (см. также [3; 13]):

u ( r , t ) = e ⁶ | ( / 1 ) g I C N ^{+ 1} ( Я ^ X n ) + ( / 1 ) E ^

N - ¹        d I ^A n 1

^' N (4,..., Xn -J )+E( /k ) E - , Г ,(18)

k=1

где I^C N ⁺¹ ( Я ,..., X n ) = J d Z J exp { i ( c^ + ^ N ^{+ 1} + ^ 0 -to

^ + XnC + Xn-1 ^N-1 + .„ + X1^)} d ^(19)

– СВК краевой волновой катастрофы C _{N +1}, а

I^{A N + 1}( Л , ^ , X n - 1 ) =

+to

= J exp { i ( £ ^{n + 1} + X n - 1 ^ ^{- 1} +.. . + Я 1 ^ ) } d ^ (20)

-to

– специальная функция сужения, то есть СВК основной волновой катастрофы A _{N +1}.

Рассмотрим теперь ситуацию, когда одновременно и s (to) ^ 0, и f (t) ^ 0, когда могут возникнуть каустики и их особенности пространственно-временных геометрооптических лучей и краевых лучей. Положение каусти- ки пространственно-временных геометрооптических лучей в пространстве R3 × T определяется системой из трех уравнений с двумя параметрами τ и ω: уравнений (7) (8) и уравнения

2 r to ^to o ^f 2 ( ^T ) ^s 2 ( ^to ) ⁺-- ^( ^{E ( to )} )

c to

- 3/2

= 1,      (21)

а каустика пространственно-временных краевых лучей – системой из двух уравнений с параметром ω:

r top- s 2(to) + з (e (to))

c to r t = t +   r—- - s1(to).(22)

c V ^E ( to )

Анализируя формулы (7–8), (21–22), легко установить, что каустики краевых лучей не пересекаются с каустикой геометрооптических лучей. Поэтому особые центральные сечения (то есть сечения, проходящие через центральную особую точку) краевых катастроф (кроме катастроф BN+1 и CN+1) в данной задаче не формируются. Однако образуются сечения каустических структур катастроф типа ^= (AN ,AN,) с такими Ng и NE, которые допустимы в соответствии с классификацией краевых катастроф (см. табл. 1 и 2, а также [13; 14]). В табл. 1 представлены особые ростки простых и некоторых унимодальных краевых катастроф, а в табл. 2 – воз- мущения. Кроме того, в табл. 1–2 введены обо- L – коразмерность особенности, M – модаль-значения: N = Ng + NE – кратность особенности, ность катастрофы, a – функциональный модуль.

Таблица 1

№	∑	∑ g	∑ E	Особый росток ϕ Ο Σ	N	L	M	æ
1.	B 2	A 1	A 1	± ζ 2	2	2	0	1
2.	C 2			ξζ ± ξ 2				2
3.	B N + 1	AN	A 1	± ζ N + 1	N + 1	N	0	1
4.	CN + 1	A 1	A N	ξζ ± ζN + 1	N + 1	N	0	2
5.	F 4	A 2	A 2	± ζ 2 ± ξ 3	4	3	0	2
6.	K 4,2	A 3	A 3	ζ 2 + aξ 2 ζ ± ξ 4	6	4	1	2
9.	# K 1,2 N - 3	A 2 N	A 3	( ζ + ξ 2 ) 2 + aξζN ; N ≥2	2 N + 3	2 N + 1	1	2
10.	# K 1,2 N - 4	2 N - 1	A 3	( ζ + ξ 2 ) 2 + aζN ; N ≥3	2 N + 2	2N	1	2
11.	KN ,2	A 3	N - 1	aζ 2 + ζξ 2 ± ξN ; N ≥5	N + 2	N	1	2
12.	K 8**	A 4	A 4	ξ 5 + ζ 2 + aζξ 3	8	6	1	2

Таблица 2

№	∑	Возмущения: ϕ 1 Σ ,..., ϕ L Σ	Ограничения на функциональный модуль а
1.	B 2	ζ	—
2.	C 2	ξ ( ζ )	–
3.	B N + 1	ζ ,..., ζ N	–
4.	C N + 1	ξ ,..., ξ N ( ξ ,..., ξ N-1 , ζ )	–
5.	F 4	ξ , ζ , ξζ	–
6.	K 4,2	ξ , ξ 2 , ζ , ξζ	a 2 ≠±4
9.	# K 1,2 N - 3	ζ ,..., ζ N , ξζ 0 ,..., ξζ N-1 , ξ 2	a ≠0
10.	# K 1,2 N - 4	ζ ,..., ζ N-1 , ξζ 0 ,..., ξζ N-1 , ξ 2	a ≠0
11.	KN ,2	ξζ , ξ ,..., ξ N-2 , ζ	a ≠0
12.	K 8 **	ξ , ξ 2 , ξ 3 , ζ , ξζ , ζξ 2	–

ВЕСТНИК 2016

Для того чтобы составить универсальную деформацию особенности, необходимо, выбрав катастрофу (строчку в таблице), записать особый росток из табл. 1 и аддитивно добавить к нему возмущения из табл. 2 с коэффициентами λ_i .

Положения центров краевых катастроф можно определить, пользуясь необходимыми и достаточными условиями, приведенными в табл. 3 [4; 13–18].

ВЕСТНИК 2016

Таблица 3

Е	Е g , Е e	æ	Необходимые и достаточные условия Общее условие: Ф1 = Ф2 = Ф3 = 0
BN + 1	AN A 1	1	Ф , k = 0, k = 1,..., N ; Ф1 n + i * 0
CN + 1	A 1 AN	2	Ф 2 k = 0, k = 1,..., N ; Ф 2 n + 1 *0, Ф 12 * 0
F 4	A 2 A 2	2	Ф 12 =Ф 22 = 0; Ф 11 *0; Ф 222 *0
K 4,2	A 3 A 3	2	Ф2222 * 0 ; Ф„ * 0 Ф 222 =Ф 22 = Ф 12 = 0; Ф 11 Ф 2222 * 3 Ф 2 22
K N ,2	А з A n - 1	2	Ф 2 k = 0, k = 1,..., N -1; Ф 2 n *0 Фп *0; Ф12 = 0; Ф122 *0; N >5
K 1#,1	A 4 A 3	2	Ф 22 = Ф 12 = Ф 222 = 0 ; Ф 2222 * 0; Ф 11 * 0 Ф 11 Ф 2222 = 3Ф 222 ; Ф 21 Ф 22222 * 10 Ф 11 Ф 122 Ф 1222 - 15 Ф 112 ( Ф 122 ) 2
K 1#,2	A 5 A 3	2	Ф 22 =Ф 12 =Ф 222 = 0 ; Ф 2222 * 0 ; Ф 11 * 0 Ф 11 Ф 2222 = 3Ф 122 ; Ф 11 Ф 22222 = 10 Ф 11 Ф 122 Ф 1222 - 15 Ф 112 ( Ф 122 ) ; Ф 31 Ф 222222 * 15 Ф 121 Ф 12222 Ф 122 + 15 Ф 111 Ф 322 — -45 Ф 11 Ф 1122 Ф 222 + 10 [ Ф 11 Ф 1222 - 3 Ф 112 Ф 122 ] 2
K 8 **	A 4 A 4	2	Ф 22 = Ф 12 = Ф 222 = Ф 122 = Ф 2222 = 0 ; Ф 22222 Ф 11 * 0

В общем случае равномерная асимптотика выражается по формуле (подробнее см. [13, 14]):

- Jig        ЯТ2

U ( - t ) = e * « ' 1 ) g I " ( $ ) + Z ( l k ) g T$T + [                  k = 2        О $_k — J

, - \ N E               "  E 1

+ ('J E I"' ($' ) + £( 'k ) E _ ^ .         (23)

k = 2        О $ k — J J

Здесь I " ( S ) - СВК краевой волновой катастрофы S = (S _g , S E ), S = ( S^g , S E ) - аргументы СВК, включающие коэффициенты (Z) и функциональные модули ( a ), I " E ( S^E ) - специальная функция сужения катастрофы на границу т = 0, то есть СВК основной волновой катастрофы типа Σ _E , N_g – кратность (число лучей) геометрооптической катастрофы Σ _g , N_E – кратность (число лучей) краевой катастрофы Σ _E .

В частности, если

1                    \2                 1

s(to) = - a(to-to0) , f (т)= 2Ьт2,         (24)

то образуется сечение краевой катастрофы F 4 = (A 2 , A 2 ). На рис. 7 и 8 показаны сплошными тонкими линиями пространственно-временные геометрооптические лучи, толстой линией с точкой обрыва – каустика пространственновременных геометрооптических лучей, штриховыми линиями – пространственно-временные краевые лучи и толстой непрерывной линией – каустика краевых лучей. Предельный геометрооптический луч касается как каустики геометрооптических лучей, так и каустики краевых лучей, но в разных точках:

1 f 1      ) а а rcg = ^5^0 — “ / rcE =-в ; “ < 0’

Г ед >  Г сВ ; ^в = " Г ( ^W ) — ^3/2.

^ 0

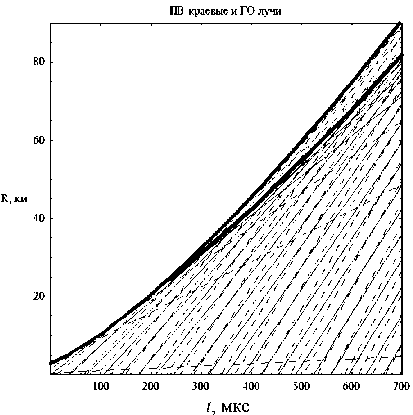
Рис. 7. Лучевая и каустическая структуры, b = 1500 c ^-1, a = -1,4 10^-11 сс

На рис. 8, являющемся фрагментом рис. 7, видно, что каустики не пересекаются.

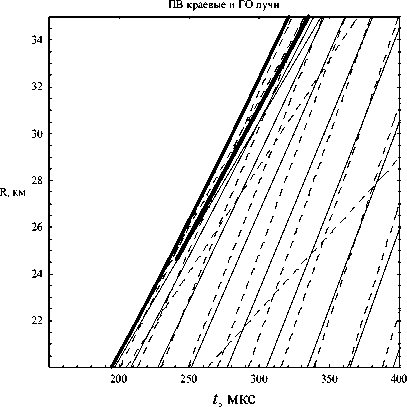
Рис. 8. Лучевая и каустическая структуры, фрагмент рис. 7, b = 1500 c ^-1, a = -1,4 10^-11 с ²

– СВК краевой волновой катастрофы F₄, +to

A ± ( X ) = I ^A 2 ( X ) = J exp { i ( ± Z ³ + XZ ) } d ^ (27) -to

– функция Эйри (СВК основной волновой катастрофы A2).

Аналогично могут быть исследованы и более сложные краевые особенности. Например, равномерная асимптотика радиосигнала в случае унимодальной краевой катастрофы K4,2 [19] имеет вид:

u ( r,t ) = e * { ( / 1 ) g IK^4,2 ( a ; Л , ЛЛ . , Л 4 ) +

+(^) ^ + (/,) ^ + (/)t ia. (л,Л) +

2Jg dЛ3      3Jg dЛ4 VIEE-2/

A3

+ ( /2 ) E ^T +( /3 ) E ^Tf ■( d Лу          о Л2 I где IK422 (a;X,X2,X„X4) = +j dZ +j exp{ i (Z2 + 0 -to

+ a Z²Z ± ^ ³ + X 1 Z + X 2 Z ² + X 3 Z + X 4 ZZ ) } d Z (29)

– СВК краевой волновой катастрофы K4,2,

+to

I ^A 3 ( X , X ) = J exp { i ( ± Z ³ + XZ + X 2 Z ²) } d Z (30)

-to

– функция Пирси (СВК основной волновой катастрофы A3).

Таким образом, в настоящей работе рассмотрен подход, лежащий в основе применения теории краевых волновых катастроф [13; 20–21] к описанию распространения частотно-модулированных радиосигналов в холодной плазме – ионосфере Земли [23]. Приведены лучевые и каустические структуры для простых (нуль-модальных) катастроф B _{N +1}, C _{N +1}, F₄ и равномерные асимптотики как для простых пространственно-временных краевых особенностей, так и унимодальных.

ВЕСТНИК 2016

Равномерная асимптотика радиосигнала в случае особенности F4 имеет вид:

u ( r, t ) = e i ®

f

U / 1 ) I F ⁴ ( X„X 2 , X ) + ( 1 2 ) — + [ gg

+ (I,) E A +( M12 ) E ^^1 -(25)

ox где IF4 (X,XX) = J dZJ exp{ i (±Z2 + ^ 0 -to

^ + Z3 + XZ + X2Z + XZZ)} dZ(26)