Классификация реляторов по доминантным признакам

• ¹    Ульяновский государственный технический университет

• ²    Ульяновский филиал Военной академии тыла и транспорта

Приведена классификация реляторов - логических схемных элементов универсального применения, воспроизводящих бинарные операции ряда алгебраических логик (специальных алгебр и математических логик) в континуальной, дискретной (включая двузначную булеву алгебру логики) областях.

Логико-алгебраические основы реляторной схемотехники

Реляторы являются логическими схемными элементами, воспроизводящими бинарные (базовые) операции импликативной алгебры выбора (ИАВ) [1]

Z 1 =^Л I ⁽ У 1^, У 2⁾ = У 1 ^{1( х}2 - x 1 ) + У 2 ^{1( х}1 - ^x2 ) , (1а)

^Z2 = ^V 1 ⁽ У 1 ,У 2 ^{) =} У 1 ¹⁽ У ^{- Х}2 ⁾⁺ У 2 ^{l( x}2 ^{- Х}1 ) (1б)

и сопутствующие им изломные и разрывные элементарные функции.

B(1) I(x) есть единичная функция (оператор Хевисайда) равная нулю при при x<<0 и единице при x>0, I(0) е {0,1}, I=(I₁₂, I₂₁) -кортеж (вектор) весовых коэффициентов, ^I12 = ^I(x1^-X2^{), I}21 = ^1-I12 = ^I(x1^-X2^), I 12^+I21 = 1 ⁽ у^сёо-вие комплементарности), у 1 и y₂ - предметные переменные (в общем случае любые физические и математические объекты, удовлетворяющие условиям мультипликативного выделения y i - 1=y i и поглощения y i -0=0), x 1 и x₂ - предикатные переменные (действительные числа).

При отождествлении предметных и предикатных переменных (y 1 = x 1 , y₂= x₂) операции ИПА-конъюнкции (1а) и ИПА-дизъюнк-ции (1б) вырождаются в базовые бинарные операции непрерывной логики (НЛ) [2-4]

Z 1 = Л(x₁,x₂) = min(X 1 ,X 2 ), Z ₂ = V(x₁,x₂) = max(x 1 ,x₂).

Если континуальные переменные в (2) принимают k разрешённых уровней, то выражение (2) вырождается в бинарные операции многозначной (k-значной) логики (МЛ), которые при k=2 являются конъюнкцией

Z 1 = x 1 Л х₂ и дизъюнкцией Z₂ = x 1 V х₂ двузначной булевой алгеброй выбора (БА).

В свою очередь ИПА-операции являются частными реализациями бинарных операций предикатной алгебры выбора (ПАВ) [5, 6]

Z 1 =^{Л (} У 1 ,У 2 ) = У 1 « 2 ⁺ У 2 « 1 ,

Z2 = ^У1,У2) = У1«1 + У2«2 , где а1е {0,1}, а2е {1,0}, а1+а2=1 (условие комплементарности весовых коэффициентов а1 и а2), А=(а1, а2) - кортеж весовых коэффициентов.

Выражения (1) - (3) воспроизводят различного типа операции альтернативного выбора в континуальной и дискретных (включая двузначную) областях в едином элементном базисе реляторов [7]. В свою очередь выражения (3) при а 1 +а₂=1 (условие комплементарности) являются базовыми операциями комплементарной алгебры (КА) [5, 6], при этом условии бинарности а 1 ,а₂е {0,1} не накладывается.

Указанные алгебраические логики (специальные алгебры и предметные логики) входят в базовую ветвь логико-алгебраической метасистемы, порождаемой функцией-аксиомой взвешенных степенных средних [8].

Принципиальным отличием импликативной алгебры выбора от других алгебраических логик заключается в том, что ИАВ определена на двух множествах - множествах предметных Ye {y 1 , y₂,...,y_n} и предикатных Xe {x 1 , x₂,...,x m } переменных, что необозримо расширяет её функциональные и алго-

à)

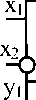
RL

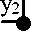
á)

x 1

I

Z

x 2

y 1

y 3

RL ^I

y 2

y 4

â)

Z 1

x 1

RL x2

Z 2

Z 1

Z 2

ã)

Рис.1. Виды реляторов ритмические возможности (включая ИАВ-модели).

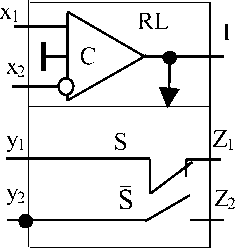
Классификация реляторов

Реляторы содержат один (рис.1) или два компаратора C i , которые управляют состоянием группы замыкающих S i и размыкающих S i аналоговых ключей. На компараторные и переключательные входы реляторов подаются соответственно предметные y 1 , у 2 и предикатные x 1 , x 2 переменные.

Номенклатура различного типа реляторов естественным образом разделяется по признаку физической природы предметных y i и предикатных x i переменных - напряжения и (или) тока. В реляторах используются следующие типы компараторов: нестробируе-мые, стробируемые, с однобитной памятью (с триггером защёлкой), дифференциальные, инвертирующие и неинвертирующие.

В зависимости от вида сигналов (напряжения U c , U s , токи I c , I s ), подаваемых на компараторные и переключательные входы соответственно различают реляторы: потенциальные RL(U c , U s ), токовые RL(I c , I s ), потенциально-токовые RL(U c , I s ), токово-потенциальные RL (I c , U s ).

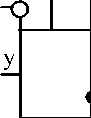
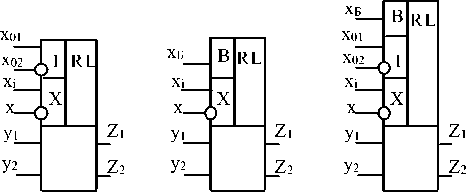
По числу переключательных каналов реляторы подразделяются на одноканальные (рис.1 а, б), двухканальные (рис.1 в) и многоканальные [а.с. СССР 1270777]. Зачернёнными кружками на рис.1 обозначены переключательные выводы размыкающих ключей реляторов, незачернёнными кружками - инвертирующие компараторные входы реляторов. По признаку объединения выводов ключей переключательных каналов различают реляторы коммутационные (рис.1 а, К-реляторы), мультиплексорные (рис.1 б, в, М-реляторы) и демультиплексорные (рис.1 г, Д-реляторы) [7].

По признаку наличия основных и дополнительных управляющих функций реляторы разделяются на четыре группы.

• 1)    Реляторы с фиксированной воспроизводимой операцией (либо ИАВ-конъюнкция, либо ИАВ-дизъюнкция). Например, К - ре-лятор по рис. 1а при объединённых переключательных выходах (Z 1 =Z₂) воспроизводится ИАВ-дизъюнкция (1б).

• 2)    Кодоуправляемые реляторы [10]. Здесь на управляющий вход релятора подаётся логический сигнал fe {0,1}, переключающий тип воспроизводимой операции: конъ-

  
• юнкцию (1а) на дизъюнкцию (16) и обратно.

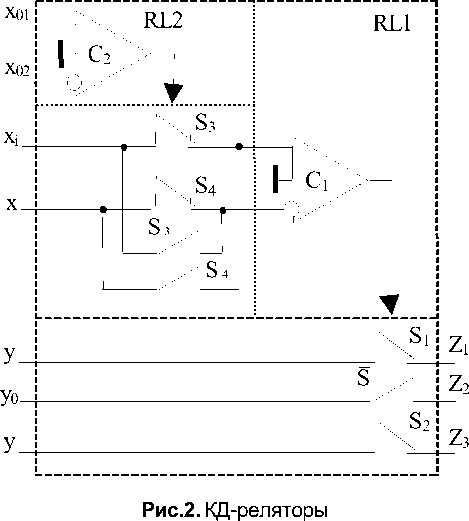
• 3)    Конъюнктивно - дизъюнктивные (КД) реляторы (рис.2) [11, 12].

Здесь на управляющие (инверсные I) входы релятора RL подаются аналоговые сигналы (напряжения) x 01 , x 0 ₂. Принципиальное отличие КД-реляторов от кодоуправляемых заключается в том, что управляющие напряжения x 01 , x 0 ₂ могут быть использованы в качестве информационных и (или) логических сигналов. Это обеспечивается совместимостью (совпадением) допустимых диапазонов изменения предикатных x 1 , x 2 и управляющих x₀₁, x₀₂ сигналов. Указанное существенно расширяет их функциональные и управляющие возможности. Например, если x₀₁= x₀₁(t) и x₀₂= x₀₂(t) являются заданными функциями текущего времени, то переключение выходного процесса Z=Z(t) осуществляется в моменты времени, когда x₀₁(t) и x₀₂(t) пересекаются. Тем самым обеспечивается КД - модуляция выходного процесса Z(t). В частном случае при фиксированных значениях управляющих сигналов (например, при x₀₁=0 или x₀₂=0) КД-релятор вырождается в кодоуправляемый.

В КД-реляторе (рис.2) на компараторе С 1 и ключах S 1 , S и S 2 собран основной реля-тор RL1 с введённым в его состав дополнительным релятором RL2, содержащим управляющий компаратор и ключи S 3 , S 4 , S 3 , S 4 . При x₀₁> x₀₂ ключи S 3 , S 4 замкнуты, а S 3 S 4 разомкнуты. При этом напряжения x i и x поступают соответственно на неинвертирующий и инвертирующий входы компаратора С 1 При x₀₁< x₀₂ имеем обратную картину и напряжения x i , x поступают соответственно на инвертирующий и неинвертирующий входы компаратора С₁. Тем самым обеспечивается инверсия воспроизводимой ИАП-операции на дуальную.

• 4)    Реляторы с блокировкой переключательных каналов воспроизводят операции

Z = t^ICV x2) + У2I(X2 - x1)]"J, (4) где x1, x2 и y1, у2 есть соответственно предикатные и предметные переменные (сигналы), J=I(xB) - управляющий логический сигнал блокировки, Z1, Z2- выходные выводы соот ветственно замыкающего S и размыкающего S ключей переключательного канала.

Согласно (4), при I(xB)=1 операции, воспроизводимые реляторами первой и данной групп, совпадают. Соответственно при I(xB)=0 ключи переключательного канала разомкнуты (режим блокировки) и воспроизводится операция "запрет прохождения сигнала".

При объединении переключательных выходов Z 1 и Z 2 (Z 1 =Z 2 =Z) или входных переключательных входов релятора (y 1 =y₂=y) приходим соответственно к мультиплексорному или демультиплексорному релятору. В частном случае для построения канала блокировки и коммутации ключей может быть использован мультиплексор КР1531КП7 [13].

• 5)    Пятую группу составляют реляторы с инверсией (I) и блокировкой (B) сигналов. Здесь совмещаются операции, воспроизводимые второй, третьей и четвёртой групп: инверсия (взаимозамещение) типа воспроизводимых базовых операций (ИАВ-конъюнкция W ИАВ-дизъюнкция) на дуальные и операция блокировки ("Запрет прохождения коммутируемых сигналов").

На рис.3 представлены условные схемные изображения КД-реляторов (рис.3а), B-реляторов (рис.3б) и IB-реляторов (рис.3в).

Воспроизводимые мультиплексорным IB-релятором (выходы Z 1 и Z 2 на рис.3в объединены Z 1 =Z 2 =Z операции определяются выражением:

Z = ЕуД^ Xi + a2 Х2) +

+ У i I( a 2 X i + a 1 X 2 )] I( X ) ’ ⁽⁵⁾ где весовые коэффициенты a 1 , о ₂е{-1,1}, I(X)=J есть единичная функция управляющая

^{а)                       б} )                      в)

Рис.3. Условные схемы КД-реляторов

включением режима блокировки.

Согласно (5), при a 1 =-1, a ₂=1 и a 1 =1, a ₂=-1 IB-реляторы при I(X)=1 воспроизводят соответственно ИПА - конъюнктивную и ИПА - дизъюнктивную операции.

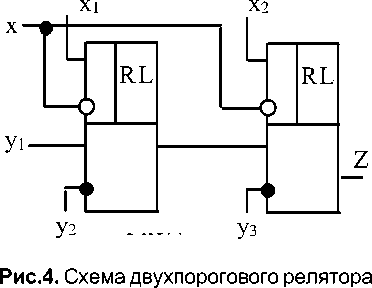
По признаку числа используемых компараторов реляторы подразделяются на одно-компараторные (однопороговые) и двухком-параторные (двухпороговые ДР) [а.с. СССР 1381548, 1501098, 1513480, 1568060] [14, 15], воспроизводимые операции и функции которых имеют соответственно одну и две точки разрыва (излома).

В зависимости от выбранных логических законов управления ключами двухпороговые (двухкомпараторные) реляторы подразделяются на двух-, трёх- и четырёх по-зиционные[14].

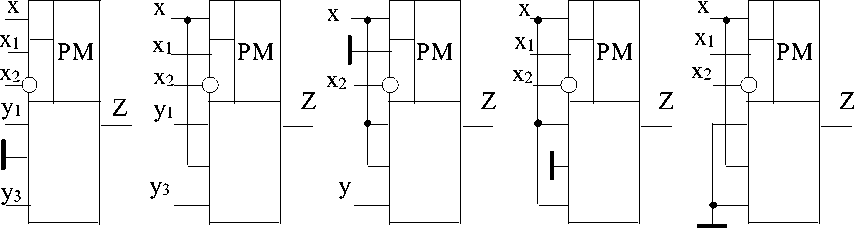
В частности, на рис.4 представлена схема двухпорогового релятора, содержащего два однопороговых релятора. В зависимости от заданной комбинации соединения выводов релятора по рис.4 (коммутационное программирование) и от заданных уровней предметных переменных он воспроизводит ряд линейно-разрывных и линейно-изломных функций. На рис.5 представлены некоторые типовые функции, воспроизводимые релято-ром по рис.4.

Релятор по рис.5а воспроизводит функцию двухпорогового компарирования (функцию допускового контроля), реляторы по рис.5б,в воспроизводят соответствено функции двустороннего и одностороннего параллельного ограничения входного сигнала х, реляторы по рис.5г, д являются соответственно режекторным (рис.5г) и селекторным (рис.5д) фильтрами уровней сигнала х.

Реляторы классифицируются также по признаку использования в различных предметных областях [16-29], что характеризует универсальность и многообразие применений логико-алгебраического (ЛА) аппарата импликативной алгебры выбора и, соответственно, реляторов и реляторной схемотехники.

Многообразие типов и номенклатуры не ограничивается потенциальными и токовыми реляторами. Здесь не рассматривались оптоэлектронные, пневматические реляторы, реляторы с трансформаторно-токовыми ком-

Z

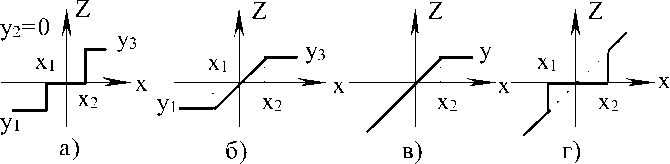
Рис.5. Типовые функции, воспроизводимые реляторами

I

x

д)

параторами, время-импульсные реляторы и др.

Работа выполнена при поддержке гранта Т00-3.3-2659 Минобразования РФ.