Классификация режимов работы фотоприемников в системах локации
Автор: Рогачев В.А.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 3 т.6, 2008 года.
Бесплатный доступ
На основании предложенной математической модели выходного сигнала фотоприемника определены все возможные режимы работы фотоприемников и произведена их классификация. Для каждого режима определены соответствующие алгоритмы обнаружения и произведено их сравнение.
Короткий адрес: https://sciup.org/140191251
IDR: 140191251 | УДК: 621.383(043)
Текст краткого сообщения Классификация режимов работы фотоприемников в системах локации
На основании предложенной математической модели выходного сигнала фотоприемника определены все возможные режимы работы фотоприемников и произведена их классификация. Для каждого режима определены соответствующие алгоритмы обнаружения и произведено их сравнение.
Постановка задачи
Одним из важнейших факторов, определяющих основные характеристики систем локации, является пороговая чувствительность. По типу шумов, ограничивающих пороговую чувствительность, выделяют следующие режимы работы фотоприемника [1-2]:
-
- режим ограничения внутренним (тепловым) шумом;
-
- режим ограничения фоновым шумом (или просто фоном);
-
- также выделяют режим ограничения флуктуациями сигнала («сигнальными шумами»).
Однако определение общего количества возможных режимов работы фотоприемников и установление взаимосвязи между режимами является задачей, изученной лишь для некоторых частных случаев и не имеющей общего решения. Такое положение, в свою очередь, не позволяет определить и синтезировать алгоритмы обнаружения для различных режимов и тем самым оптимизировать построение системы локации.
Решение
Анализ существующих фотоприемников, таких как фотодиоды, фоторезисторы, приборы с зарядовой связью и многие другие, позволяет выделить в выходном сигнале две составляющие – постоянную составляющую и шумовую составляющую.
Постоянная составляющая выходного сигнала фотоприемника имеет две компоненты [1; 35] – темновой ток, то есть ток, присутствующий на выходе фотоприемника при полном отсутствии внешней освещенности, и фоновый ток, то есть ток, обусловленный фоновой (внешней) освещенностью. Более сложная ситуация наблюдается с шумовой составляющей [1-5].
Все возможные ситуации относительно шумов можно разделить на два типа:
-
- шумы, не зависящие от постоянной составляющей, то есть аддитивные шумы (например, тепловые);
-
- шумы, пропорциональные постоянной составляющей, то есть мультипликативные шумы (например, фотонные).
Эти шумы обусловлены различными причинами и различным образом воздействуют на параметры системы обнаружения. Наличие шумов ограничивает потенциальную чувствительность ИК системы.
Для описания распределения выходного сигнала фотоприемника используем модель нормального распределения. Такая модель достаточно хорошо согласуется с распределениями множества выходных сигналов фотоприемников и имеет всего два параметра – математическое ожидание и дисперсию, она хорошо исследована математически. Полагаем, что корреляция шумов в выходном сигнале матричного фотоприемника, как правило, невелика, поэтому она не учитывается в модели.
Учитывая эти положения, модель выходного сигнала фотоприемника представим некоррелированным гауссовским (нормальным) случайным процессом. Математическое ожидание имеет три составляющие – темновой ток, фоновый ток и полезный сигнал, а дисперсия также имеет три составляющие, обусловленные внутренним шумом, фоновым током и полезным сигналом:
y e N(d + b + s,a2 + ab + as),
где y – выходной сигнал фотоприемника при наличии полезного сигнала, d – темновой ток, b – фоновый ток, s – сигнальный ток, σ 2 – дисперсия внутренних шумов, ab – дисперсия фоновых шумов, as – дисперсия сигнальнозависимых шумов, a – коэффициент пропорциональности между постоянной составляющей выходного сигнала и его дисперсией, зависящий от типа применяемого фотоприемника.
При отсутствии полезного сигнала выходной сигнал фотоприемника изменяется, пропадают полезный сигнал и пропорциональные ему сигнальные шумы y e N ( d + b ,^ 2 + ab ) .
Для двухвыборочной модели и проверяемых гипотез о наличии H 1 и отсутствии H 0 полезного сиг-нала,математическая модель имеет следующий вид:
H 0 : x e N ( d + b , a 2 + ab ), y e N ( d + b , a 2 + ab ) ;
H1: x^N(d ^b,^ + ab),y^N(d+b+s,^ +ab+as).
С учетом того, что производится решение задачи обнаружения, на основе полученной математической модели выходного сигнала фотоприем-никапроизведемклассификациюматематических моделей и соответствующих им режимов работы фотоприемников. Для этого используем следующие признаки:
-
а ) параметры распределения вероятностей, относительно которых проверяются гипотезы;
-
б ) условия, при которых из общей математической модели следуют частные случаи.
Математическая модель выходного сигнала фотоприемника во всех случаях описывается нормальным распределением с двумя параметрами – математическим ожиданием и дисперсией. Таким образом, принципиально возможны только три различные ситуации изменения параметров:
-
- одновременное увеличение математического ожидания и дисперсии;
-
- увеличение математического ожидания;
-
- увеличение дисперсии.
В общем случае проверяется гипотеза об одновременном увеличении и математического ожидания s > 0 , и дисперсии as > 0 , а математическое ожидание и дисперсия имеют по три составляющие. Никаких ограничительных условий на соотношение параметров выходного сигнала в этом случае не накладывается. В этих условиях справедлива общая математическая модель:
H 0 : x e N ( d + b , a 2 + ab ), y e N ( d + b , a 2 + ab ) ;
H1: x^N(d+b,rf + ab),y^N(d+b+s,o2 + ab+as).
При проверкегипотезы об увеличении математического ожидания s > 0 , когда влияние фонового тока, а также фоновых и сигнальных шумов мало d >> b , a 2 >> ab + as , получаем модель, описывающую работу фотоприемника в режиме ограничения внутренним шумом [1]
H0 : x e N(d,a2),y e N(d,a2) ;
H 1 : x e N(d,a2),y e N(d + s,a2) .
При проверке гипотезы об увеличении дисперсии as > 0 , когда существенно только влияние сигнальных шумов d + b >> s , a >> 1 , получаем модель, описывающую работу фотоприемника в режиме ограничения «сигнальным шумом» [2]
H 0 : x g N ( d + b , c2 + ab ), y e N ( d + b , c2 + ab ) ;
H1: xeN(d■ b.^ + ab), y eN(d+b,o2 + ab+ as).
При проверке гипотезы об одновременном увеличении и математического ожидания s > 0 , и дисперсии as > 0 , при условии, когда темновой ток и внутренние шумы весьма малы: d << b , c 2<< ab + as , получаем модель, описывающую работу фотоприемника в режиме ограничения фоном [1]
H0 : x g N(b, ab), y g N(b, ab);
H 1 : x g N ( b , ab ), y g N ( d + b + s , ab + as ) .
Данный режим является частным (вырожденным) случаем общего режима при условии, когда параметры выходного сигнала фотоприемника полностью определяются внешним излучением.
Эта классификация разбивает все множество моделей на четыре класса, в зависимости от проверяемых параметров, соотношения компонент помехи и степени связи между дисперсией и математическим ожиданием.
Для рассмотренных режимов работы фотоприемника определим статистики, позволяющие решить соответствующие задачи обнаружения в каждом из режимов.
Для режима ограничения внутренним шумом известна оптимальная решающая статистика Стьюдента, а для режима ограничения сигнальным шумом известна оптимальная решающая статистика Фишера [6-7].
Однако для общего режима и режима ограничения фоном оптимальные решающие статистики определены только для известных параметров [6; 8].
Для решения задачи обнаружения полезного сигнала в режиме ограничения фоном при наличии мешающего параметра – фона определено равномерно наиболее мощное (РНМ) несмещенное правило обнаружения [9]. В этом режиме, в отличие от остальных режимов, существуют только квадратичные статистики [9].
Это правило основано на условном распреде-N лении статистики v = ∑ y 2j при фиксированном j =1 NM значении u = ^ yj2 + ^ xi2 . Оно заключается в j=1 i=1
сравнении статистики – нецентральной статистики Пирсона с пороговым уровнем A v ( и ) , зависящим от значения, которое приняла статистика u [9]:
Hо: v < Av (u) , Hi: v > Av (u).
Таким образом, алгоритм решающей статистики заключается в сравнении суммы квадратов значений сигналов элементов сигнальной области с пороговым уровнем, неявно зависящим от суммы квадратов значений сигналов элементов сигнальной области и фоновой областей.
Необходимость решения неявного уравнения, содержащегодвойнойбесконечный ряд,дляопре-деления порогового уровня в темпе поступления информации резко повышает вычислительные затраты при практической реализации полученного РНМ правила.
Для того чтобы преодолеть это препятствие, было определено более простое приближенное правило, основанное на нецентральной статистике Фишера [9].
Гипотезы H 0 и H 1 принимаются в случае:
NM н0: Z У^ Z Xi2 < Xq j=1 i=1
NM
H i : Z У 22 / Z x 2 > X q , j = 1 i = 1
где X q = (1 - a ) 2/N /[1 - (1 - a ) 2/N ] — пороговый уровень [9].
Таким образом, решающая статистика представляет собой отношение сумм квадратов значений сигналов элементов сигнальной к фоновой области. От известной статистики Фишера, применяемой в режиме ограничения сигнальным шумом, она отличается отсутствием центрирования в числителе и знаменателе.
Задача обнаружения полезного сигнала в общем режиме сходна с двухвыборочной задачей сравнения математических ожиданий при неравных дисперсиях, задачей, не имеющей решения (проблема Беренса-Фишера) [7; 10].
В рассматриваемом случае задача обнаружения полезного сигнала в общем режиме не имеет единственного решения вследствие связи между дисперсией и математическим ожиданием (отсутствия полноты статистик), а из-за того, что проверяется два параметра (многомерная альтернатива), задача не имеет РНМ критерия [7; 10].
Системы данного класса имеют весьма важное значение, поскольку на практике, как правило, в системе присутствует несколько различных типов шумов. Решение задачи обнаружения для таких условий получено только при известных параметрах фона и сигнала [6]. Естественно, это не отвечает реальным условиям обнаружения, когда существует априорная неопределенность как сигнала, так и фона [11].
Синтез правила обнаружения с использованием инвариантных преобразований из группы сдвигов и масштабов приводит к решающему правилу – модифицированной статистике Фишера [12]:
NM
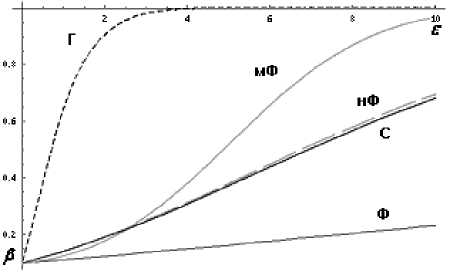
H0 :[Z NM H :[Z(Уj -x)2 /N]/[Z(Xi -X)/(M-1)]< Xz, j=1 i=1 M где x = ∑ xi / M – среднее значение по фоновой i =1 области; Xz = FNXM-1{1 - a} - пороговый уровень; FNXM-1{1 — a} - квантиль распределения Фишера уровня α с N и M - 1 степенями свободы [12]. Данная решающая статистика представляет собой отношение оценки дисперсии по сигнальной области к оценке дисперсии по фоновой области. В отличие от обычной статистики Фишера, в числителе используется оценка математического ожидания фоновой области, в которой отсутствует полезный сигнал. Это позволяет учесть то, что при появлении полезного сигнала произойдет как увеличение математического ожидания, так и дисперсии. Применение теории инвариантности – преобразований из класса сдвигов и масштабов дает возможность получить статистику для проверки выдвинутой гипотезы, однако судить о степени ее близости к РНМ можно лишь в сравнении с решающими статистиками для сходных задач. Рассмотрим применение алгоритмов обнаружения для всех четырех режимов в условиях общей модели. Это позволит сравнить алгоритмы в одинаковых условиях. К тому же, меняя параметры модели, можно будет оценить устойчивость того или иного алгоритма к изменению параметров исходной модели. Приведем зависимости вероятности правильного обнаружения сигнала от отношения сигнал/ шум в диапазоне ε = 0...10 для всех статистик при различных значениях параметров. Вычисления вероятностей правильного обнаружения были произведены при изменении относительного уровня фона τ в диапазоне от 0,1 до 10 и изменении нормированного коэффициента пропорциональности между средним и дисперсией θ в диапазоне от 0,1 до 10 для вероятности ложной тревоги 0,1 и при числе элементов фоновой области M = 10 и числе элементов сигнальной области N = 10. Расчеты также показывают что при изменении вероятности ложной тревоги до 0,01 и 0,001, а также увеличении объемов фоновой и сигнальной областей до 100 характер поведения кривых вероятности правильного обнаружения не изменяется. Рис. 1. Вероятности правильного обнаружения β в зависимости от отношения сигнал / шум ε : Ф – статистика Фишера; мФ – модифицированная статистика Фишера; нФ (длинный пунктир) – нецентральная статистика Фишера; С – статистика Стьюдента; Г (короткий пунктир) – статистика Гаусса при всех известных параметрах; при τ = 1 и θ = 1 Рис. 2. Вероятности правильного обнаружения β в зависимости от отношения сигнал/ шум ε : Ф – статистика Фишера; мФ – модифицированная статистика Фишера; нФ (длинный пунктир) – нецентральная статистика Фишера; С – статистика Стьюдента; Г (короткий пунктир) – статистика Гаусса при всех известных параметрах; при τ = 20 и θ = 1 Как видно из приведенных графиков, при малом уровне шумовой составляющей сигнала статистика Стьюдента и модифицированная статистика Фишера обеспечивают превосходство по сравнению со статистикой Фишера. Расчеты показывают, что превосходство одной статистики над другой зависит от отношения сигнал/шум. При малых отношениях сигнал/ шум, большом уровне фона и малом уровне шу- мовой составляющей сигнала статистика Стьюдента обеспечивает превосходство над всеми остальными. Однако уже при значении отношения сигнал/шум более двух модифицированная статистика Фишера начинает превосходить статистику Стьюдента по мощности. Это объясняется тем, что статистики Фишера хорошо реагируют на шумовую компоненту сигнала, а в данном случае она невелика. Кроме того, большой уровень фона подавляет сигнал. Поэтому статистики, пригодные во всех остальных случаях, при большом уровне фона и малом уровне шумовой составляющей сигнала оказываются малоэффективными. При малом уровне фона и большом уровне шумовой составляющей сигнала, напротив, нецентральная статистика Фишера намного превосходит все остальные и практически приближается к идеальной кривой Гаусса со всеми известными параметрами, а мощность статистики Стьюдента опускается практически до нуля. Интерес представляет рассмотрение вариантов с одинаково малыми или большими уровнями фона и шумовой компоненты сигнала. При одинаково малых фоновой и шумовой компонентах сигнала все статистики обладают достаточно высокой мощностью. При одинаково больших значениях фоновой и шумовой составляющих сигнала модифицированная статистика Фишера и центрированная статистика Фишера обеспечивают стабильное превосходство над остальными статистиками при всех значениях отношения сигнал/шум. Таким образом, вычисления вероятностей правильного обнаружения всех четырех статистик показывают: Для различных отношений сигнал-шум, фона и коэффициента пропорциональности – модифицированная статистика Фишера и центрированная статистика Фишера обеспечивают превышение вероятности правильного обнаружения в 1,5-2,5 раза, при отношении сигнал-шум, равном 2, над статистиками Стьюдента и Фишера. Лучшие характеристики по сравнению с остальными статистиками при небольших относительных значениях фона обеспечивает нецентральная статистика Фишера, а при больших относительных значениях фона – модифицированная статистика Фишера. Выводы 1. Для описания выходного сигнала фотоприемника предложена математическая модель, позволяющая обобщить известные модели вы- 2. Предложена классификация моделей выходного сигнала и соответствующих им режимов работы фотоприемника, разбивающая все множество моделей на четыре класса в зависимости от проверяемых параметров, соотношения компонент помехи и позволяющая учесть степень связи между дисперсией и математическим ожиданием. 3. Для каждого режима определены соответствующие алгоритмы обнаружения и произведено их сравнение.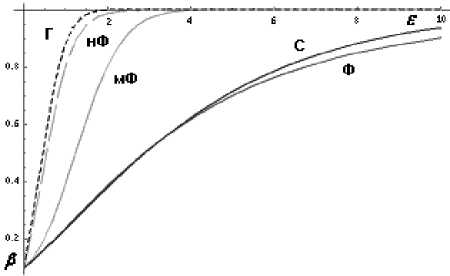
Список литературы Классификация режимов работы фотоприемников в системах локации
- Хадсон Р. Инфракрасные системы. М.: Мир, 1972.-535 с.
- Фотоприемники видимого и ИК диапазонов. М.: Радио и связь, 1985. -328 с.
- Ллойд Дж. Системы тепловидения. М.: Мир, 1978.-414 с.
- Полупроводниковые формирователи сигналов изображения. Под ред. П. Йесперса, Ф. Ван де Виле и М. Уайта. М.: Мир, М., 1979. -574 с.
- Полупроводниковые фотоприемники: ультрафиолетовый, видимый и ближний ИК диапазоны спектров. Под. ред. В.И. Стафеева. М.: Радио и связь, 1984. -216 с.
- Кендалл М., Стьюарт А. Статистические выводы и связи. Мир, М., 1966. -400 с.
- Леман Э.Л. Проверка статистических гипотез. Наука, М., 1978.-408 с.
- Богданович В.А. Применение принципа несмещенности в задачах обнаружения с априорной неопределенностью//Известия ВУЗов СССР. Радиоэлектроника. Т. 15, № 4, 1972. -С. 453-460.
- Рогачев В.А. Выделение сигналов в ТВ системе на матричном фотоприемнике с чувствительностью, лимитированной флуктуациями фона//Техника средств связи. Сер. «Техника телевидения». Вып. 4, 1989. -С. 83-89.
- Кокс Д., Хинкли Д. Теоретическая статистика. М.:Мир, 1978.-560с.
- Анцев Г.В., Волков В.Ю., Макаренко А.А., Рогачев В.А., Турнецкий Л.С. Цифровые методы обнаружения объектов на тепловых изображениях поверхности моря,//Труды РНТО
- им. А.С. Попова. Серия «Цифровая обработка сигналов и ее применение». Вып. VIII, № 1-2, 2006. -С. 294-298.
- Рогачев В.А. Влияние неравномерности чувствительности фотоприемника на выделение сигналов в ТВ системах при внутренних и фоновых шумах//Техника средств связи. Серия «Техника телевидения». Вып. 5, 1990. -С. 31-40.


