Классификация символов в стенографических документах на основные, надстрочные и под строчные

Для правильной дешифровки исторических стенографических документов [4] требуется определить тип каждого символа (графемы), то есть отнести его к основным, надстрочным или подстрочным символам. Из-за искажений рукописного текста, связанных с привычками автора, скоростью письма, аккуратностью, наклоном текста в ту или иную сторону, заваливанием, исправлением, зачеркиванием текста и некоторыми другими факторами, точно решить эту задачу невозможно. В работе [3] предлагается математическая модель дешифровки стенограмм. Использование этой модели предполагает знание вероятности того, что стенографический символ относится к основным, надстрочным или подстрочным. В данной статье описываются два алгоритма вычисления этих вероятностей и результаты сравнения их работы. Оба алгоритма используют метод аппроксимации, так как проведенный анализ показал, что строки в стенографических документах, как правило, имеют форму, которую можно аппроксимировать полиномом некоторой степени.

Для объективного сравнения качества работы алгоритмов классификации символов была построена контрольная последовательность, то есть в стенографических документах были выделены строки и для каждого символа указан его тип. Оценки были рассчитаны путем сравнения результатов работы алгоритма классификации символов с контрольной последовательностью. Были рассмотрены корректность, которая рассчитывается как отношение количества правильно классифицированных символов к общему количеству символов, точность, полнота и F-мера [6] для каждого типа символов, а также обобщенная F-мера, представляющая собой среднее значение оценок F-меры для каждого типа символов.

При оценке считалось, что символ относится к тому или иному типу, если вероятность данного события превышала 50 процентов. Кроме того, разбиение символов на строки выполнялось с помощью алгоритма распознавания строк методом построения графа связей, описанного в работе [1]. В качестве итоговой оценки, на основании которой проводилось оценивание качества алгоритмов классификации символов, была выбрана обобщенная F-мера.

АЛГОРИТМ КЛАССИФИКАЦИИ СИМВОЛОВ МЕТОДОМ ОДИНАРНОЙ АППРОКСИМАЦИИ

Задается степень аппроксимирующего полинома m [5]. Предположим, что для каждого стенографического символа известны его размеры и то, к какой строке он относится. Строим полиномиальную аппроксимирующую функцию

степени m по центрам символов одной строки (рис. 1). Кривую, заданную аппроксимирующей функцией, будем называть линией аппроксимации. Определяем расстояния между центрами символов и линией аппроксимации. Обозначим это расстояние для некоторого символа за е . Тогда вероятность того, что данный символ является основным, будем считать равной

P осн = e ^{- λε} , (1)

а вероятность того, что данный символ является надстрочным, в случае если он расположен над линией аппроксимации, либо подстрочным, если он расположен под линией аппроксимации, равной

-λε неосн e

,

где X - некоторый коэффициент, который подбирается в зависимости от стенограммы. При этом Pосн

+ P

= 1.

неосн

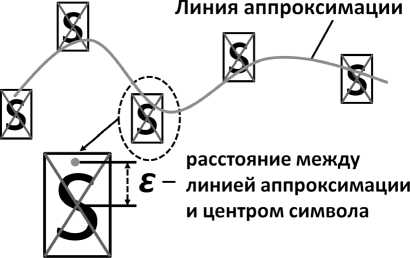
Рис. 1. Распознавание типов символов методом одинарной аппроксимации

О

Таблица 1

Лучшие средние значения обобщенной F-меры алгоритма классификации символов методом одинарной аппроксимации

m	λ	Обобщенная F-мера
		Стенограмма				Среднее значение
		№ 1	№ 2	№ 3	№ 4
4	0,0473	0,4696	0,5831	0,5661	0,6728	0,5729
4	0,0474	0,4696	0,5831	0,5661	0,6728	0,5729
4	0,047	0,4686	0,5831	0,5661	0,6728	0,57265
4	0,0481	0,4776	0,5726	0,5613	0,6728	0,571075
4	0,0471	0,4655	0,5831	0,5661	0,6728	0,571875
4	0,0472	0,4655	0,5831	0,5661	0,6728	0,571875
4	0,0487	0,4733	0,5883	0,5613	0,6613	0,57105
4	0,0488	0,4733	0,5883	0,5613	0,6613	0,57105
4	0,0475	0,4696	0,5795	0,5629	0,6728	0,5712
4	0,0476	0,4696	0,5795	0,5613	0,6728	0,5708
4	0,0682	0,5087	0,5169	0,5012	0,5405	0,516825
1	0,0326	0,3618	0,6744	0,5031	0,523	0,515575
4	0,0419	0,3825	0,5697	0,5854	0,6336	0,5428
3	0,0377	0,3924	0,5991	0,5135	0,6945	0,549875

Для алгоритма классификации символов методом одинарной аппроксимации были получены значения обобщенной F-меры на четырех стенографических документах при различных значениях настроечных параметров. Значения коэффициента X брались из диапазона от 0,025 до 0,155 с шагом 0,0001, а значения степени аппроксимирующего полинома – из диапазона от 0 до 10 с шагом 1. В табл. 1 приведены лучшие средние значения обобщенной F-меры. Последние четыре строки таблицы содержат максимальные значения обобщенной F-меры для каждой из стенограмм. При этом средние значения обобщенной F-меры в этих строках оказались заметно хуже, чем в остальных строках таблицы.

АЛГОРИТМ КЛАССИФИКАЦИИ СИМВОЛОВ МЕТОДОМ ДВОЙНОЙ АППРОКСИМАЦИИ

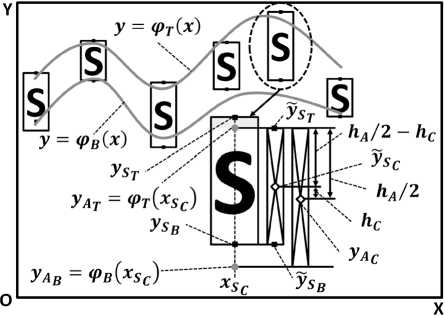
Задается степень аппроксимирующего полинома m . Для символов одной строки построим две полиномиальные аппроксимирующие функции: одну ф _т ( x ) по точкам, являющимся серединами верхних сторон, и другую ф _в ( x ) по точкам, являющимся серединами нижних сторон прямоугольников, в которые вписаны символы строки. При этом верхняя и нижняя стороны каждого такого прямоугольника параллельны оси абсцисс.

Пусть некоторый символ S вписан в прямоугольник, центр которого находится в точке с абсциссой xS , тогда аппроксимирующая функция, построенная по серединам верхних сторон прямоугольников, описывающих символы строки, принимает в данной точке значение yT = фт(xsC), а аппроксимирующая функция, построенная по серединам нижних сторон прямоугольников, описывающих символы строки, принимает значение y ав фв(xsc). Точки, лежа- щие на верхней стороне прямоугольника, описывающего символ S , имеют ординату yST , а точки, лежащие на нижней стороне, имеют ординату ySB . Определим новые значения ординат yST и ySB , которые зависят от взаимного расположения линий аппроксимаций и сторон прямоугольника, описывающего символ S .

Для	y S T :
если	ysT >  y а, , тогда ysT = y. ;
если	ys, <  y AB , тогда y S = y A ; TB   TB
если	yAK ys, yA, , тогда ys = ys BT T    TT

Аналогично для y S :

B

Классификация символов в стенографических документах на основные, надстрочные и подстрочные

• •    если y s _B >  y T. , тогда y sb = y^ ;

• •    если ySB <  yAB , тогда y SB = yAB ; BB   BB

• •    если yAB " ysB " yAB , тогда y sb = ysB . BBT   BB

После чего выполним следующие действия:

• •    определим ординату центра отрезка, параллельного оси OY, ординаты концов которого равны соответственно y _A и y_A , и обозначим ее за y ;                     ^{T B}

AC

• •    определим ординату центра отрезка, параллельного оси OY, ординаты концов которого равны соответственно yS_T и y S , и обозначим ее за У S ;

приведены лучшие средние значения обобщенной F-меры.

Таблица 2

Лучшие средние значения обобщенной F-меры алгоритма классификации символов методом двойной аппроксимации

m	Обобщенная F-мера
	Стенограмма				Среднее значение
	№ 1	№ 2	№ 3	№ 4
4	0,5591	0,6886	0,5462	0,6756	0,617375
4	0,5524	0,6246	0,6287	0,6405	0,61155
4	0,5572	0,7172	0,4914	0,675	0,6102
4	0,5572	0,6	0,6506	0,6104	0,60455
4	0,5607	0,6558	0,5618	0,6344	0,603175

• •    определим длину отрезка, параллельного оси OY, ординаты концов которого равны соответственно y _A и y_A , и обозначим ее за h _A ;

• •    определим длину отрезка, параллельного оси OY, ординаты концов которого равны соответственно y _A и у S , и обозначим ее за h C .

Вероятность того, что символ S является основным, примем равной

P осн

( h A /2 - h e - h_A /2

ОЦЕНКА АЛГОРИТМОВ КЛАССИФИКАЦИИ СИМВОЛОВ

В табл. 3 представлены лучшие оценки алгоритмов классификации символов методом одинарной аппроксимации и методом двойной аппроксимации на стенографических документах, приведенных в предыдущих таблицах.

Таблица 3

Лучшие оценки алгоритмов классификации символов

а вероятность того, что символ S является над-

строчным ^{( y} S C >  Уа,_с ) ^или подстрочным ^{( y} S C <  y ,_c ),

Оценка	Алгоритм классификации символов
	Методом одинарной аппроксимации	Методом двойной аппроксимации

равной

= h C .

h A /2

На рис. 2 представлена схема с обозначениями, используемыми в вышеописанном алгоритме.

СТЕНОГРАМ МА № 1 (SAVE_LOG_DSCN4795)

Корректность	0,724			0,8368
Тип символов	Осн.	Надстр.	Подстр.	Осн.	Надстр.	Подстр.
Полнота	0,7838	0,5333	0,4854	0,952	0,2667	0,4078
Точность	0,8651	0,1143	0,5495	0,8617	0,2	0,84
F-мера	0,8225	0,1882	0,5155	0,9046	0,2286	0,549
Обобщенная F-мера	0,5087			0,5607

СТЕНОГРАМ МА № 2 (SAVE_LOG_DSCN4859)

Корректность	0,8728			0,8902
Тип символов	Осн.	Надстр.	Подстр.	Осн.	Надстр.	Подстр.
Полнота	0,9422	0,7333	0,3784	0,9558	0,6667	0,4595
Точность	0,9142	0,55	0,6087	0,9183	0,6667	0,68
F-мера	0,928	0,6286	0,4667	0,9367	0,6667	0,5484
Обобщенная F-мера	0,6744			0,7172

Рис. 2. Распознавание типов символов методом двойной аппроксимации

СТЕНОГРАМ МА № 3 (SAVE_LOG_DSCN4868)

Корректность	0,8418			0,8955
Тип символов	Осн.	Надстр.	Подстр.	Осн.	Надстр.	Подстр.
Полнота	0,9052	0,5625	0,375	0,9706	0,5	0,375
Точность	0,9203	0,375	0,4138	0,9224	0,5333	0,7059
F-мера	0,9127	0,45	0,3934	0,9459	0,5161	0,4898
Обобщенная F-мера	0,5854			0,6506

Для алгоритма классификации символов методом двойной аппроксимации были получены значения обобщенной F-меры на четырех стенографических документах, приведенных в предыдущей таблице, при значениях степени аппроксимирующего полинома, которые брались из диапазона от 0 до 10 с шагом 1. В табл. 2

СТЕНОГРАМ МА № 4 (SAVE_LOG_DSCN4871)

Корректность	0,8915			0,9009
Тип символов	Осн.	Надстр.	Подстр.	Осн.	Надстр.	Подстр.
Полнота	0,9834	0,625	0,2609	0,9945	0,5	0,3043
Точность	0,899	1	0,6667	0,9	0,8	1
F-мера	0,9393	0,7692	0,375	0,9449	0,6154	0,4667
Обобщенная F-мера	0,6945			0,6756

Как видно из приведенных результатов, на трех из четырех стенограмм алгоритм классификации символов методом двойной аппроксимации показал наилучший результат. Это связано с тем, что алгоритм распознавания надстрочных и подстрочных символов методом двойной аппроксимации менее чувствителен к размерам символов. Он учитывает и верхние, и нижние границы символов, а алгоритм распознавания надстрочных учитывает только центры символов, при этом возможна такая ситуация, когда центр крупного символа, который является основным в строке, совпадает с центром надстрочного или подстрочного символа.

ЗАКЛЮЧЕНИЕ

Рассмотренные в статье алгоритмы будут реализованы в создаваемой компьютерной программе для распознавания исторических стенограмм [2].

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ на 2012–2016 гг.

CLASSIFICATION OF SYMBOLS IN SHORTHAND DOCUMENTS: BASIC, SUPERSCRIPT AND SUBSCRIPT