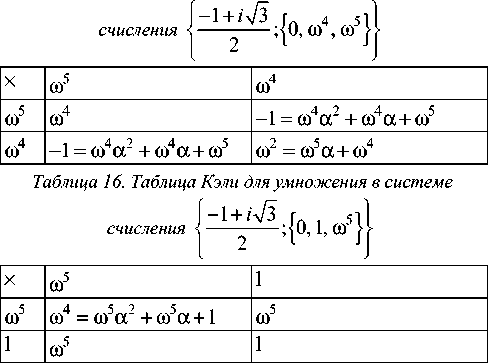Классификация тернарных квазиканонических систем счисления в мнимых квадратичных полях и их приложение

Целью настоящей работы является классификация одного класса троичных систем счисления в мнимых квадратичных полях. Актуальность работы определяется двумя факторами.

Во-первых, троичные системы счисления не часто, но всё же использовались в приложениях, например, в докомпьютерную эру Д.И. Менделеев интересовался тернарной уравновешенной системой счисления и на её основе разработал цифровой ряд значений весов разновеса для взвешивания на лабораторных весах, который используется по сей день [1, 2]. Позднее Джоном Фон Нейманом [3] было показано, что именно троичная система счисления наиболее экономична. В данном случае под экономичностью понимается возможность представления как можно большего диапазона чисел с использованием как можно меньшего общего количества состояний триггеров, составляющих регистры, которые и описывают представления чисел в некоторой системе счисления. Развитие же «экономичной» троичной вычислительной техники тормозилось в основном технологическими причинами.

В наше время, несмотря на скептическое высказывание Д. Кнута [4] относительно перспектив применения так называемой троичной уравновешенной системы счисления (то есть позиционной системы счисления с основанием 3 и цифрами { - 1,0,1 } ), эта система всё же применяется, например, при создании электронных устройств, что объясняется тем, что умножение в такой системе счисления производится без переносов, а в таблице сложения переносы в старшие разряды присутствуют лишь в двух случаях.

Во-вторых, в работах И. Катаи и Б. Ковача [5, 6] введено понятие канонических систем счисления, экстраполирующее теорию систем счисления на случай квадратичных полей. Следует отметить, что И. Катаи, Б. Ковач и их последователи рассматривают только тот случай, когда конечное множество цифр состоит из целых рациональных чисел. В работах [5, 6, 7] ими получены классификационные теоремы для канонических систем счисления во всех квадратичных полях. Кроме того, Ковачем [8] найдены эффективные рекуррентные алгоритмы вычисления цифр представления элементов в канонических системах счисления.

В данной работе мы классифицируем тернарные системы счисления в мнимых квадратичных расширениях, предполагая, что цифрами в них являются целые квадратичные элементы. Такие системы счисления в статье называются квазиканоническими. В отличие от цитируемой работы [8] для нахождения цифр представления элементов в квазиканонических системах счисления синтезируются алгоритмы, основанные на алгоритме деления с остатком в некоторых квадратичных кольцах.

Основные определения

Определение 1. Пусть Q ( d ) есть квадратичное поле [9]:

Q(Id) ={z = a + bld; a,be Q}, где d – целое число, свободное от квадратов. При d > 0 квадратичное поле называется вещественным, а при d < 0 - мнимым.

Если норма Norm ( z ) = ( a + bld )( a - bld ) = = a ² - db ² элемента z = a + bld e Q ( Id ) и его след Tr ( z ) = ( a + bld ) + ( a - bld ) = 2 a есть целые числа, то этот элемент называется целым алгебраическим числом поля Q ( d ) [10].

Хорошо известно [9], что целые алгебраические числа мнимого поля Q(iVAj , где d < 0 , A = |d| , имеют вид z = ^

a + bid A ;

a + bi VA.

2;

Кольцо целых обозначать S(Id)

a , b e Z при A = - 2, - 3 ( mod 4 ) ;

a , b e Z , a = b ( mod2 ) при

A = -1( mod 4).

элементов поля Q ( Id ) будем

.

Определение 2. Целое алгебраическое число a = A±Id (при d = 2,3(mod 4)) или a = 2(B±dd) (при d = 1( mod 4)) называется основанием канонической системы счисления (КСС) в кольце S (Id) целых элементов поля Q( d) , если любой целый элемент этого поля однозначно представим в форме конечной суммы

k ( z )

z = £ aj aj , j=0

a j e I = { 0,1,...,| Norm ( a )| - 1 } .

Пара { a ; I } называется канонической системой

Q ( d ) , если любой целый элемент этого поля представим в форме конечной суммы k ( z )

z = £ a j a j , a j e I , j = 0

где множество I состоит из целых алгебраических чисел, по норме меньших нормы основания a .

Пара { a ; I } называется квазиканонической сис-

счисления (КСС) в кольце

S ( Vd ) , а I — алфавитом

этой системы [10].

В работах [8] для представления целого алгебраического числа в таких системах применяется рекуррентный алгоритм. Однако с той же целью можно использовать и деление с остатком, реализуемое лишь в некоторых кольцах [11]. В настоящей работе рассматриваются только мнимые кольца.

Определение 3. Говорят, что в кольце D имеет место алгоритм деления с остатком, если на отличных от нуля элементах pe D определена функция ||Р||, принимающая целые неотрицательные значения,

так, что выполняются следующие условия:

• 1)    если р^ 0 делится на a, то ||P||>||a||;

• 2)    для любых элементов р и a^ 0 в D сущест

вуют такие у и r , что в = ay+ r , причём либо r = 0,

либо || r || <  ||a||.

Утверждение.

Среди колец

s (4d)

целых эле-

ментов мнимых квадратичных полей Q (V d ) алгоритмом деления с остатком по норме обладают те и только те, для которых d равно одному из следующих пяти значений: { - 1, - 2, - 3, - 7, - 11 } [9].

Стоит отметить, что числа у и r в равенстве в = ay+ r определяются неоднозначно, поскольку

существует несколько различных остатков r , имеющих одну и ту же норму. Это позволяет рассматри-

вать различные системы счисления с одним и тем же основанием a , но разными алфавитами (множествами цифр).

Если в качестве элементов множества I рассматривать не целые рациональные (обычные целые), а целые алгебраические числа, то можно получить целый класс систем счисления. Например, в поле Q ( i V3) в качестве цифр можно рассматривать числа

1 + i У3 - 1 + i У3

2, 2

а в качестве основания –

темой счисления в кольце

S ( 4d ) , а I - алфавитом

этой системы.

Тернарные квазиканонические системы счисления

Определение 5. Квазиканоническая система счисления с основанием a и алфавитом I называется тернарной системой счисления в поле Q (V d ) , если

Norm ( a ) = 3 и алфавит I состоит из трёх цифр.

В табл. 1 указаны числа z , имеющие нормы 1, 2 и 3 в мнимых квадратичных полях, для которых существует алгоритм деления с остатком.

Таблица 1. Числа с нормами 1, 2 и 3 в полях

Q ( i ) , Q ( i V2 ) , Q ( i V3 ) , Q ( i V? ) , Q ( i VT1 )

z d	1	2	3
-1	±1; ± i	± 1 ± i	нет
-2	±1	± i 41	± 1 ± i 41
-3	±l±z'V3 ±1; -----3 2	нет	± i V3;         3 2
-7	±1	± 1 ± i 4l 2	нет
-11	±1	нет	± 1 ± i У1Г 2

Из этой таблицы следует, что тернарные квазика-нонические системы счисления могут существовать только при d = - 2, - 3, - 11.

Используя табл. 1, можно легко получить возможные комбинации оснований систем счисления и множества остатков.

Сформулируем в виде лемм ряд свойств, справедливых для любых тернарных квазиканонических систем счисления.

Лемма 1. Если Norm ( a ) = 3 , то равенство в = ay+ r равносильно равенству

- 3 + i 4з

.

Определение 4. Целое алгебраическое число a называется основанием квазиканонической системы

Y =

(в-r )a

счисления в кольце

s (4d)

целых элементов поля

где a - число, сопряжённое a .

Лемма 2. Если для пары { a ; I } доказано, что представление произвольного целого алгебраическо-

го числа Y 0 в форме Y 0 = Y _i а + r₀ единственно, где r ₀ е I , то для того, чтобы пара { а ; I } образовывала систему счисления, достаточно, чтобы представление числа Y 0 являлось конечным, то есть процесс деления с остатком:

Yo = Yi •«+Г),

Yi = Y2 •«+ri,

Y1 = Y 1+i -а+ri, где r0, r1, ..., rle I , был конечен. Другими словами, существует такое l, что Yl +1 = 0, а для этого, в свою очередь, достаточно, чтобы Norm (ym+1 )< Norm (ym) Vm = 0,1,..., l.

Определение 6. Системы счисления { а ; I } и

{ а' ; I ' } в кольце

s (4d)

называются эквивалентны-

ми, если существует взаимно однозначное отображе-

ние

f : S ( 4d ) ^ S ( 4d ) , причём f ( I ) = I' ,

такое,

что

для любого числа

Ye S(4d) ,

представимого в

N системе счисления {а; I} в виде y = Е apаp , где p=o ap e I, число f (y) в системе счисления {а'; I'} за-

N писывается в виде f (y) = Е f (ap )(а')p . Стоит от-p=o

метить, что а' не обязательно равно f ( а ) .

Лемма 3. Если r – первообразный корень из еди-

ницы степени, равной количеству чисел с единичной

нормой (единиц поля) в кольце

S (Vd)

то системы

счисления { а ; I } к = 0,1,2, ....

и { а ; I • r k } эквивалентны, где

Доказательство. Действительно, если для y ₀ , представимого в системе счисления { а ; I } , справед-

ливо равенство Y 0 =Y ₁ а+ r ₀, то, умножая это равенство на r , получим, что число Y ₀ r имеет такую же запись в системе счисления { а ; I • r k } , как и y ₀ в сис-

теме счисления { а , I } , то есть если y ₀

N

= Е apаp , то p=0

N

Y ₀ r k = Е ( a p r k ) а p . Это означает, что p =0'

ления { а ; I } и { а ; I • r k } эквивалентны.

системы счис-

Лемма 4. Если а

число

комплексно-

сопряжённое числу а , а I состоит из чисел ком-

плексно-сопряжённых числам из I , то системы счисления { а ; I } и { а ; I } эквивалентны.

Доказательство. Действительно, если взять сопряжение от обеих частей равенства Y 0 = Y ₁ a+ r ₀, то получим y ₀ =Y ₁ а+ r ₀, то есть число Y 0 имеет такую же запись в системе счисления { а ; I } , как и число Y 0 в системе счисления { а ; I } . Следовательно, системы счисления { а ; I } и { а ; I } эквивалентны.

Замечание 1. Очевидно, что если f – функция, переводящая систему счисления { а ; I } в эквивалентную ей систему { а' ; I ' } , то алгоритм сложения двух чисел f ( y ) и f ( в ) в системе счисления { а' ; I ' } легко получается из алгоритма сложения чисел Y и в в системе счисления { а ; I } . То же самое можно сказать и об инверсии знака.

Замечание 2 . Если функция f задаётся равенством f ( y ) = Y , где Y — число, сопряжённое Y , то алгоритм умножения двух чисел у и в в системе счисления { а ; I } также легко получается из алгоритма умножения чисел Y и в в системе счисления { а ; I } . Если же функция f отличается от указанной выше, то алгоритм умножения в системе счисления { а' ; I ' } если и может быть получен из алгоритма умножения в системе счисления { а ; I } , то только нетривиальным образом.

Тернарные квазиканонические системы счисления в S ( i Jb )

Элементы кольца целых чисел Эйзенштейна, то есть кольца S ( i Jb ) , представимы в виде

a + bi V3 z =---2---; a, b e Z; a = b(mod2).

Так как в кольце S ( i 3) нет элементов, норма которых равна двум, то при делении с остатком по норме на а норма ненулевого остатка может равняться только единице. Таких остатков довольно много: {2( ± 1 ± i V3), ± 1} , что в сочетании с вариантами выбора а : {2( ± 3 ± i V3), ± 73} даёт 1/2 x 6 x (6 - 1) x 6 = 90 потенциальных комбинаций возможных оснований а и множеств I , то есть тернарных квазиканонических систем счисления. Заметим, что в алгоритме деления с остатком по норме однозначно определяется не сам остаток, а только его норма. И, следовательно, при достаточно широком выборе элементов с одинаковой нормой возникает проблема выбора таких остатков, т. е. «цифр», при котором последовательное деление с ос-

татком на основание α приведёт к получению конечного представления элемента именно в тернарной системе. Требование конечности представления чисел в системах счисления существенно ограничивает выбор α и I , что описывается следующей основной теоремой.

Теорема 1. В кольце целых алгебраических чисел S ( i 3) существуют ровно 24 тернарные квазиканони-

ческие системы счисления, а именно: системы счисления с основаниями a k = ( i V3) to k - 1 и множествами цифр

{0,1, to }, {0, to , to ² }, {0, to ² , to ³ },

r 1 = 2 ( mod3 ) . В этом случае для каждого целого алгебраического числа β однозначно определяется r и по формуле (3) однозначно вычисляется γ.

Так как остатки r , кроме r =0, являются числами единичной нормы, то они могут быть записаны в виде to a и to ^b . Найдём теперь соотношения между a и b . Для этого переберём все 6 чисел с нормой, равной 1, и выясним, у каких из них r ₁ = 1 ( mod 3 ) , а у каких -

{0, to ³ , to ⁴ }, {0, to ⁴ , to ⁵ },{0, to ⁵ , to ⁶ };

где to =1/2(1 + i V3) и k = 1,2,3,4.

Доказательству теоремы предпошлём ряд лемм.

Лемма 5. Пусть ae S ( i4b ) является основанием тернарной системы счисления, для которой множество цифр I выбирается из чисел r e S ( i V3 ) , причём

r ₁ = 2 ( mod 3 ) . Несложно убедиться, что r 1 = 1 ( mod3 ) для to ¹ , to ³ , to ⁵ , а r 1 = 2 ( mod3 ) - для всех остальных. Следовательно, все возможные системы остатков могут быть представлены в виде I = { 0, to ^a , to ^b } , где a , b = 1,2,3,4,5,6 и

II d

.

Тогда

I = {0, toa, tob }

, где

to = 1/2(1 + iV3), a,b = 1,2,3,4,5,6 или b = a + 3(mod6).

и

b = a +1( mod 6)

Доказательство.

Пусть

e = a 0 ¹ ч

,

a₀= b₀ (mod 2);

r 2

,

r1 = r₂(mod2) и

b = a +1 (mod 6) или b = a + 3 (mod 6).

Таким образом, показано, что в системах счисления {an; I} возможно однозначное представление произвольного целого алгебраического числа из поля Q (i V3).

Рассмотрим теперь конечность представления чисел в таких системах счисления, опираясь на лемму 2.

Лемма 6. В равенствах (2) найдётся такой элемент l, при котором Norm (yl₊₁) < 1.

Доказательство. Выясним, для каких систем остатков условие       Norm ( y _m+1) < Norm (Y_m)

Vm = 0,1,..., l выполняется для каждого целого ал-

~ c + di V3

a =----2----, c = d (mod2),    a₀, b₀, c, d, r1, r₂e Z .

Подставляя выражения для p, a и r в формулу (1),

имеем

Y =

ca₀- 3 db₀+ 3 dr₂- cr1

+

a₀d - r1 d + cb₀- cr₂

i 3. (3)

Поскольку у - целое алгебраическое число поля

Q (i), то Re у и Im y должны быть целыми рациональными числами. Учитывая, что c = 0(mod3) , а также условия сравнимости a₀= b₀(mod 2); r1 = r₂(mod2); c = d(mod2), получаем, что Re Ye Z , а числитель Im y делится на 2. Далее несложно заметить, что cb₀- cr₂ делится на 3. Таким образом, получаем Im Ye Z о a₀= r1 (mod3) . При этом условии легко убедиться в том, что Im y-Re Y = 0 (mod 2), то есть Im y = Re Y(mod2).

Поскольку a₀ – любое целое рациональное число,

то из доказанного следует, что для однозначности представления (1) необходимо и достаточно, чтобы множество остатков состояло ровно из трёх чисел, для каждого из которых выполняется только одно из следующих условий: r1 = 0(mod3); r1 = 1(mod3);

гебраического числа γm.

V = am^{+ b}mi ^3   Г = rm 1 ⁺rm 2 i

Пусть     Y m       2     , rm        2          ’ am, bm, rm 1, rm2 e Z   . Согласно формулам (2)

_м A (Ym^-rm )^a(Ym^-rm )^a

Norm ( Ym+1 ) =----3---3----

Norm (Ym^-rm )

Подставляя последнее выражение в неравенство

am^{+ 3b}m

Norm (y_m+1)< ^m 4—m , после преобразований полу-

чаем

। rm 1 I am + т /         \22,-12

.       2 )            Г2д I    rm1 ^{+ 3}rm2

I I                         ,>

3        ( m 2 )4

r²+ 3r²

где m¹4 m2 = Norm (rm).

Если r_m = 0 , то очевидно, что (4) выполняется для любого Y_m ^ 0 .

Если r_m ^ 0 , то Norm (r_m) = 1 и неравенство (4)

принимает вид

2 rm1

am +11 I Г Г У 2-^ + I bm + rm2 I > 1.

3 I ^m 2 I

Таким образом, условие Norm (уm+1 )< Norm (уm) выполняется для всех целых   a_m   и   b_m

(am = bm (mod 2)), за исключением тех, которые удовлетворяют неравенству 2

- +1 bm + rm2 I < 1.                     (6)

m₂

Такие am и bm будем называть исключительными и исследуем их отдельно.

Введём следующие обозначения

/        _ 1 + iV3 /       2_1 — iЛ _T

(—А) — to— —~—; (—В) — to — —~—. Тогда

А — to⁴

—1 — i У3

В — to⁵

—1 + i У3

Далее, учитывая леммы 3 и 4, легко получить, что достаточно исследовать вместо 54 лишь 6 систем счисления, а именно:

Итак, найдётся такое значение l — q, при котором Norm (уq₊₁) — 0,   следовательно,   уq₊₁— 0, либо

Norm (уq₊₁) — 1, то есть уq₊₁— to^к , где к —1,2,3,4,5,6 . Для всех этих значений уq₊₁ в системах счисления j-3 + iV[ ;{о, — 1, в}и {,■ ^.{о, — 1, в}}, легко проверить, используя табл. 2, что через конечное число шагов процесса деления с остатком появится частное Yp — 0. То же самое справедливо и для всех систем счисления, эквивалентных двум вышеназванным. В системах счисления j +2^ ;{0, — 1, в}|, j3±2V1 ;{0,1, — 1}, ।Z3±iVl ;{0,1, — 1}, {i V3;{0,1, — 1}} при последовательном применении

3 + i У3

;{0, — 1, в}

—3+IV3

;{0, — 1, в}

алгоритма деления с остатком возможно зацикливание. Поэтому в последних четырёх системах счисления и всех эквивалентных им не любое целое алгеб-

{i V3;{0, — 1, B}},

3 + i У3

;{0,1, — 1}

³ Vi^³;{0,1, — 1}, {iV3;{0,1, — 1}}.

В этих системах счисления неравенство (4) выполняется для всех у_m , кроме конечного числа исключительных случаев. Результаты исследования исключительных случаев для шести приведённых систем счисления представлены в табл. 2.

раическое число допускает конечное представление. Примеры чисел с бесконечным представлением приведены в табл. 2.

Таким образом, в поле Q (i43) существует лишь

24 системы счисления, в которых представление целых алгебраических чисел этого поля единственно и

конечно.

Из доказанного легко получается алгоритм записи

целого числа Эйзенштейна

Yo ^—

а₀+ b₀i 43 .

а₀, b₀ е Z, а₀= b₀ (mod2), в системе счисления с ос

нованием а — i 43to^k

Таблица 2. Представление чисел, удовлетворяющих неравенству (6) в исследуемых системах счисления

алфавит а \	{0,—1,1}	{0,—1, в }
3 + i 4з	B—Bа+1	—в — — в а — 1
2
—3 + i 4з	A — Аа2— а+1	1 — —а + в, —в — —а—1, А — ва+в, —А — ва^ + в а—1
2
—i 4з	А — Аа4+ а3— —а — а+1	1 — в а2— а+в, —в — в а2 — а—1, А — в а3— а2+ в а+в, —А — в а—1

и алфавитом I_k — {0, tot, tot⁺¹} ,

где к —1,2,3,4 и t — 0,1,2,3,4,5.

Алгоритм 1.

Шаг 1. Полагаем p — 0.

Шаг 2. Если для y_p —

ap⁺bpi^

a_p = 0 (mod 3),

то r_p — 0 .

Если a_p = 1 (mod 3), то r_p — tot, где t —1,3,5.

Если a_p = 2 (mod 3), то r_p — tot, где t — 0,2,4.

Шаг 3. Вычисляем   y _p+1   по формуле

_v _ (^Yp^{— r}P)^а

^Yp+1        3

.

Числа, приведённые в табл. 2, удовлетворяют неравенству (6), но при этом норма каждого такого числа равна 1, что и доказывает справедливость леммы 6.

Если y_p+1— 0, то алгоритм закончен.

Если y_p+1* 0, то p — p +1 и переходим к шагу 2.

Сходимость данного алгоритма следует из доказательства теоремы 1.

Тернарные квазиканонические системы счисления в S (i Л) и S (i V11)

Приведённый выше метод исследования обобщается и на случай колец S(i 2) и S(i 11) .

Заметим, что в S(i 2) и S(i 11) , наряду с троичными каноническими системами счисления, существуют и тернарные квазиканонические системы счисления, которые описываются следующими теоремами.

Теорема 2. В кольце целых алгебраических чисел S(i 2) существуют ровно 4 тернарные квазиканони-ческие системы счисления, а именно: системы счисления с основаниями а = ±1 ± i41 и множеством цифр I = {0,1,-1}.

Теорема 3. В кольце целых алгебраических чисел S(i 11) существуют ровно 4 тернарные квазиканони-ческие системы счисления, а именно: системы счисления с основаниями а = (±1 ± iVH)/2 и множеством цифр I = {0,1, -1}.

Реализация арифметических операций

Рассмотрим теперь арифметические операции в системах счисления, указанных в теореме 1. Сложность вычислений и основные отличия арифметики в этих системах счисления определяются в основном сложностью «правил переноса в старший разряд» при сложе-нии/умножении цифр. Эти правила достаточно просты. Например, таблицы 3–16 являются таблицами Кэли для сложения и умножения при

. r        —1 + i V3

аk = — iV3 и аk =--------.

Таблица 3. Таблица Кэли для сложения в системе счисления {—i V3;{0,1, ю}}

+	0	®	1
0	0	®	1
®	®	2® = = а3+ ®а2+ ®а+1	1 + ® = = а4+ ®а3+ а2+ а
1	1	1 + ® = = а4+ та3+ а2+ а	2 = иа+®

Таблица 4. Таблица Кэли для сложения в системе счисления

]—1 + iV3 r_n , -J

}—2—;{0,1, ®}

+	0	®	1
0	0	®	1
®	®	2® = = а3+ а2+ ®а+1	1 + ® = ®а2+ а
1	1	1 + ® = ®а2+ а	2 = ®а2+ ®а+®

Алгоритм 2 (Сложение).

Шаг 1. Складываем по разрядам два данных числа. При этом в записи суммы могут присутствовать цифры 2 ®,1 + ®, 2, не входящие в алфавит системы счисления.

Тогда переходим к шагу 2, иначе, если таковой цифры не встретилось, получаем искомую сумму.

Шаг 2. Используем формулы из табл. 3 (или 4) сложения для каждой «цифры» в записи числа, не входящей в алфавит (по одному разу для каждого разряда). При этом в записи могут появиться и другие «цифры», избавиться от которых можно применяя формулы из табл. 3 (или 4) к числам, в сумме дающим данные «цифры». После этого, двигаясь от нулевого разряда, находим первую «цифру» справа, большую единицы по норме. Эта «цифра» и все другие, стоящие слева от неё, определяют некоторый многочлен P (x) . Если P (x) делится на x²+ 3 без остатка, то считаем его «нулевым», если с остатком, то повторяем шаг 2.

Если в сумме не осталось цифр, не принадлежащих алфавиту {0,1, ®} , то получаем искомый результат.

Умножение. Реализация операции умножения даже в эквивалентных системах счисления может отличаться. В силу особенностей алфавита, а именно того, что одна из цифр является нулём, таблицы умножения для таких систем счисления сильно упрощаются, и достаточно записать разложение лишь четырёх чисел для тернарной квазиканонической системы счисления. Согласно леммам 3 и 4, алгоритм умножения чисел в системе счисления {а; I} легко получается из алгоритма умножения чисел в системе счисления {а; I} . Для примера рассмотрим алгоритм умножения в системе счисления {—iV3;{0,1, ®}}.

Таблица 5. Таблица Кэли для умножения в системе счисления {—i V3;{0,1, ®}}

X	®	1
®	®2= а3+ ®а2+ а +1	®
1	®	1

Таблица 6. Таблица Кэли для умножения в системе счисления {—iV3;{0, ®, ®²}}

X	®	®2
®	®2	—1 = = ®а3+ ®2а2+ ®а+®
®2	—1 = = ®а3+ ®2а2+ ®а+®	4      _ 2 .    2_ .    2 ® =®а +® а+®

Таблица 7. Таблица Кэли для умножения в системе счисления

{—i V3;{0, — 1, ®²}}

X	—1	®2
—1	1 = ®2а2+(—1)а+®2	®5 = = ®2а2+(—1)а+(—1)
®2	®5 = = ®2а2+(—1)а+(—1)	®4= ®2а3+(—1)а2+ +®2а+®2

Таблица 8. Таблица Кэли для умножения в системе счисления

{-i V3;{0, -1, to⁴}}

X	—1	to4
—1	1 = (—1)a2+ (—1)a+to4	to = = (—1)a2+(—1)a+(—1)
to4	to = = (—1)a2+ (—1)a+(—1)	to2= (—1)a+to4

Таблица 9. Таблица Кэли для умножения в системе счисления {— iv3;{0, to , to }}

X	to5	to4
to5	to4	3      4- .   5 to =to a+to
to4	to3= to4a+to5	2      4_ 2 .   5_ .   4 to2= to4a2+ to5a+to4

Таблица 10. Таблица Кэли для умножения в системе счисления {—iV3;{0,1, to⁵}}

X	to5	1
to5	to = to a+1	to5
1	to5	1

Таблица 11. Таблица Кэли для умножения в системе I—1 + iV3 r„ 1 -,} счисления<----2----;{0,1, to} p
X	to	1
to	to2= a+1	to
1	to	1

Таблица 12. Таблица Кэли для умножения в системе

1 — 1 + i V3           211 счисления <---------и 0, to, to 2 I           J
X	to	to2
to	to2	—1 = toa+to
to2	—1 = toa+to	4     2       2 to4= to2a+to2

Таблица 13. Таблица Кэли для умножения в системе

1 —1 + iV3 r„ 1 2] I счисления <           ;s0, 1, toff 2 I            J
X	—1	to2
—1	1 = (—1)a+to2	to5= (—1)a+(—1)
to2	to5= (—1)a+(—1)	4     2       2 to4= to2a+to2
Таблица 14. Таблица Кэли для умножения в системе I—1 + iV3 r        4]} счисления <           ;s0, 1, toff 2 I            J
X	—1	to4
—1	1 = to4a+to4	to= to4a+(—1)
to4	to= to4a+(—1)	to2=(—1)a2+ (—1)a+to4

Таблица 15. Таблица Кэли для умножения в системе

Поскольку алфавит системы счисления

{—iV3;{0,1, to}} состоит из цифр 0, 1 и to, то умно- жение чисел a и c в этой системе счисления сводится к сложению m чисел, где m – количество цифр единичной нормы в записи числа c . Складываемые числа получаются из числа a следующим образом. При умножении числа на цифру to или 1, стоящую в разряде, соответствующем ap , к записи числа a справа добавляется p нулей, а цифры заменяются согласно формулам из табл. 5 (или 6–16). Далее происходит упрощение полученного числа путём последовательного применения второго шага алгоритма сложения. Далее получившееся число складывают с результатом предыдущей операции сложения согласно алгоритму сложения.

О параллельных алгоритмах вычисления свёртки в тернарных квазиканонических системах счисления

В настоящее время для быстрого умножения больших целых чисел в основном используется алгоритм Шёнхаге–Штрассена [12] или алгоритм Фюрера [13]. До появления последнего наиболее быстрым алгоритмом умножения считался алгоритм Шёнхаге– Штрассена, основная идея которого заключалась в сведении умножения целых чисел, представленных в той или иной позиционной системе счисления, к вычислению циклической свёртки спектральным методом (с помощью дискретного преобразования Фурье (ДПФ) или его модулярных аналогов (теоретикочисловых преобразований, ТЧП).

Развитием алгоритма Шёнхаге–Штрассена можно считать алгоритмы, приведённые в работах [14, 15], которые позволяют вычислять свёртку параллельно и без умножений. В настоящей работе исследуется обобщение метода этих работ на случай квазикано-нических систем счисления. Приведём полученные результаты.

Пусть Norm(a) = 3 . Э-М числом (числом Эйзенштейна–Мерсенна) будем называть целое рациональное число вида

Mn = (an - 1)(an -1) = 3n - (an + an) +1, а Э–Ф числом (числом Эйзенштейна–Ферма) – целое рациональное число вида

Fn = (a n + 1)(a n +1) = 3 n + (an + a n) +1.

Лемма 7. При n ^ 0(mod4) сомножители (an ± 1)

и (aⁿ ± 1) взаимно просты.

Лемма 7 даёт гарантии возможности параллельного вычисления циклической свёртки (или, согласно методу Шенхаге–Штрассена, умножения целых чисел) в кольцах по модулям (an ± 1), (an ± 1) с после -дующей реконструкцией результата по модулям Mn или Fn с помощью китайской теоремы об остатках при достаточно мягких дополнительных ограничениях на арифметическую структуру Mn или Fn. Непосредственный анализ этих ограничений показал, что при 1 < n < 100, m = (an ± 1)(an ± 1) , и a , равному одному из чисел множества i V3, - i V3,

-3 + iVS -3 - iVS

2,2

вычисление свёртки длины n=1, 2, 3, 4, 5, 7, 8, 11, 13, 16, 17, 19, 23, 29, 31, 32, 37, 41, 43, 47, 53, 59, 61, 64, 67, 71, 73, 79, 83, 89, 97 можно реализовать без умножений.

Заключение

В работе подробно рассмотрен алгоритм представления чисел и реализации основных арифметических операций в кольце целых чисел Эйзенштейна. Приведена полная классификация тернарных квази-канонических систем счисления в мнимых квадратичных полях. Подробно рассмотрен случай поля Q (i V3), для которого представлено доказательство классификационной теоремы для этого случая.

Предложенный подход достаточно легко обобщается на случай других квадратичных расширений, для элементов которых существуют алгоритмы деления с остатком по норме или их аналоги.

Кроме того, в работе рассмотрена возможность применения метода параллельного вычисления произведения больших чисел [10] для тернарных квази-канонических систем счисления. В результате получены длины свёрток, которые можно использовать для быстрого вычисления произведения.

Работа выполнена при финансовой поддержке РФФИ (гранты 13-01-97007-р_поволжье_а, 12-01-00822а, 12-01-31316 мол a).