Классы преобразований нестационарного сигнала в информационно-измерительных системах. III. Время-масштабные (вейвлет-) преобразования для спектрально-временного анализа
Автор: Меркушева А.В.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Оригинальные статьи
Статья в выпуске: 3 т.12, 2002 года.
Бесплатный доступ
Представлены задачи, связанные с время-масштабными (вейвлет-) преобразованиями для спектрально-временнóго анализа и локализации свойств нестационарных сигналов сложной формы в информационно-измерительных системах. Это - речевые сигналы, сигналы в области сейсмологии, изучения океана, в технике антенн и в других системах. Представлены основы теории и метода вейвлет-преобразования: базисы и фреймы, основные типы базисов и свойства преобразований. Признаки и свойства вейвлет-преобразований систематизированы и объединены классификацией.
Короткий адрес: https://sciup.org/14264252
IDR: 14264252 | УДК: 621.391.266.037.372
Текст научной статьи Классы преобразований нестационарного сигнала в информационно-измерительных системах. III. Время-масштабные (вейвлет-) преобразования для спектрально-временного анализа
Представлены задачи, связанные с время-масштабными (вейвлет-) преобразованиями для спектрально-вре-меннóго анализа и локализации свойств нестационарных сигналов сложной формы в информационноизмерительных системах. Это — речевые сигналы, сигналы в области сейсмологии, изучения океана, в технике антенн и в других системах. Представлены основы теории и метода вейвлет-преобразования: базисы и фреймы, основные типы базисов и свойства преобразований. Признаки и свойства вейвлет-преобразований систематизированы и объединены классификацией.
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Время-масштабные преобразования образуют отдельную группу преобразований, реализующих двумерное отображение нестационарного сигнала на плоскость время—масштаб. В отличие от вре-мя-частотного преобразования [1], при котором представление сигнала отображением на плоскость время—частота легко интерпретируется (в виде мгновенного частотного спектра сигнала, данного в динамике его изменения на определенном временнóм интервале), интерпретация преобразования время—масштаб требует знакомства с элементами теории его построения.
В терминах функционального анализа или теории матриц время-масштабное преобразование — это определенным образом упорядоченное множество коэффициентов разложения сигнала по базисным функциям. Однако базис, так же как и коэффициенты разложения, представляющие результат преобразования, является двумерным. При этом одной из переменных базисной функции является масштаб — параметр, определяющий деформацию (по шкале времени) материнской вейв-лет-функции, которая образует базис вейвлет-преобразования. Именно этот способ порождения вейвлет-базиса и позволяет локализовать свойства нестационарного сигнала. Переменная масштаба а может интерпретироваться как гиперболическое преобразование частоты а = ω 0/ ω , где ω 0 — постоянная, определяющая единицы измерения связанных переменных.
Разложение при время-масштабном (вейвлет-) преобразовании получается экономичным за счет того, что разрешение по переменной масштаба является равномерным в логарифмической шкале и ячейка относительного разрешения время—масш- таб является постоянной во всем диапазоне изменения сигнала:
at
Предварительные замечания относительно время-масштабного преобразования будут полно раскрыты в следующем ниже систематическом изложении принципов построения время-масштабных преобразований и их свойств, которые определяют практический выбор типа преобразования в соответствии с видом решаемой задачи обработки сигнала и интерпретации результата. Для этого необходимо рассмотреть теоретические основы метод*а время-масштабного (вейвлет-) преобразования *), его методическую базу — базисы и фреймы, определение основных типов вейвлет-преобразования, проанализировать и систематизировать их свойства.
БАЗИСЫ И ФРЕЙМЫ
Понятие базиса включает наличие ряда линейно независимых функций, с помощью которых функция-сигнал может быть выражена как линейная комбинация с постоянными коэффициентами.
Метод фреймов, введенный в [2] для представления сигнала, обеспечивает более гибкую схему анализа [3], [4]. Фреймы обобщают понятие базиса, т. к. при сходстве формы представления сигнала у фрейма сняты ограничения единственности разложения, не требуется линейной независимости компонент фрейма и ортогональности (почти всегда предполагаемой у базиса). Представление о базисах и фреймах относится к сигналам с непрерывным и дискретным временем. Поэтому принят формализм векторного пространства, где базис v = { v i( t ), v 2( t ),..., v n ( t )} и фрейм h = { h i( t ), h 2( t ),..., h n ( t )} — это векторы, а t е [ T 1 , T 2 ] или является множеством точек отсчетов t = t i, t 2,., tm .
Базис ортогонален при условии
( v i ’ v j > = k j • 5 j , где
5 y = 1 если i = j , (2)
5,., = 0 если i ^ j, ij и ортонормален, если все kj = 1.
Сигнал s ( t ), принадлежащий линейной оболочке базиса, определяется в виде разложения:
s ( t ) = С i V i ( t ) + c 2 V 2 ( t ) + ... + c n v n ( t ) + ... . (3)
При ортонормальном базисе коэффициенты разложения c i однозначно определяются по соотношению
C i =< f ( t ), V i ( t ) ) . (4)
Для представления сигнала применяются ортогональные схемы преобразования Фурье, Уолша, дискретное косинус-преобразование и вейвлет-преобразование.
Отказ от ортогональности может дать симметрию фильтров, обеспечивающих алгоритм преобразования, и важное для обработки сигналов свойство линейности фазы [5]. Однако для этого вводятся два (взаимно) биортогональных базиса, коэффициенты разложения определяются с одним базисом (анализ), а восстановленный сигнал (при его синтезе) представляется разложением по би-ортогональному базису [6-8]. Такой метод, основанный на биортогональности, реализуется во время-частотном преобразовании Габора [9-10] и в вейвлет-преобразовании [11-14]. Метод использует два базиса { v i( t ), v 2( t ),..., V n ( t ),...} и { u i( t ), u 2 ( t ),., u n ( t ),.}, называемых дуальными, или биортогональными, для которых выполняется только взаимная ортогональность
( u i ( t ), v j ( t ) > = k j • 5 ij . (5)
При биортогональности сигнал может быть представлен в двух формах разложения по любо- му из дуальных базисов, причем коэффициенты разложения определяются как скалярные произведения сигнала на дуальные базисные функции.
s = X civi’ ci = ^s’ ui ); (6) i s = X ci ui’ ci =^S’ vi ^ (7) z
Концепция дуальных базисов может быть использована при ортогональном и биортогональном представлениях сигнала. При ортогональном представлении базис и его дуальный базис идентичны, а представление сигнала рассматривается как частный случай неортогональной схемы [15].
Фрейм определяется как семейство векторов { h 1 , h 2 ,., h n ,.}, для которых выполняется условие
A||s||2 <^|< s, h.^ < BWs\?, (8) i где постоянные А и В — границы фрейма и не зависят от сигнала s.
Компоненты {h1, h2,., hn,.}можно организовать в оператор фрейма. С помощью этого оператора сигнал восстанавливается по коэффициентам {(f, h i)} i=12 n на основе итеративной процедуры. Размерность компонент фрейма соответствует размерности вектор-сигнала и для сегмента сигнала с m отсчетами равна m.. Тогда фрейм — это система m-мерных векторов hi = [ hn, hi2,..., him ]T,...,h n = [ hnl, hn 2,..., hnm Г,™’ (9) которая для любого m-мерного вектора-сигнала s из пространства, натянутого на {hi, h2 ., hn,.}, удовлетворяет условию (8) [3], [i6-i8].
Оператор фрейма S строится из компонент { h i } формированием матриц A i и их суммированием:
n
S = S A i ’ i - i
(i0)
где hii • hii hii • hi2
h i i • h im
A i = h i * hiT = .
h im • h i i h im • h i 2
h. -h.
im im
Оператор фрейма S и ему обратный S "1 ограничены:
A • I < S < B • I , (ii)
B - i • I < S - i < A - i • I . (i2)
Набор { S ^*h i } i =i_ n образует фрейм с границами В –1 и А –1, называемый дуальным. Сигнал s , представимый как линейная комбинация векторов { h i }, имеет два вида разложения: по компонентам фрейма и по компонентам его дуального фрейма. При этом коэффициенты разложения — это скалярные произведения сигнала на соответствующие компоненты дуального фрейма
n s = ∑〈s,S-1hi〉hi, (13)
i = 1
n s = ∑〈s,hi〉S-1hi. (14)
i = 1
Для фреймов и их операторов действует правило, которое позволяет вычислять нижнюю и верхнюю границы фрейма. Границами фрейма являются минимальное и максимальное значения собственных чисел оператора фрейма как матрицы, так что имеет место соотношение (15), в котором λ 1 — наибольшее, а λ m – наименьшее собственные числа матрицы S:
λ m || s ||2 ≤ ∑ | 〈 s , h i 〉 |2 ≤ λ 1 || s ||2. (15)
i
Ортогональным базисом являются фреймы с равными значениями границ А и В .
ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ КАК МЕТОД КРАТНО-МАСШТАБНОГО АНАЛИЗА
В качестве развития направления время-частотного анализа как метода двухпараметрического представления нестационарного сигнала сложной формы полезно систематизировать способы теоретического описания вейвлет-преобразования и проанализировать группу таких преобразований на основе метода кратно-масштабного анализа. Формирование теории вейвлет-преобразования основывается на работах [19–27].
Вейвлет-преобразование (ВП) обеспечивает представление сигнала s ( t ) в базисе { ψ a , b =|a| –1/2 . ψ (( t – b ) /a )} a,b с коэффициентами разложения w ( a,b ) = 〈 s , ψ a , b 〉 , где 〈 s , ψ a , b 〉 ≡
∞
≡ ∫ s ( t ) ψ a , b ( t )d t ≡ 〈 f , ψ a , b 〉 . -∞
В частотной области это представление выражается соотношениями
w(a, b) = 1 〈sˆ,ψˆab〉,(16)
2π
ψˆa,b(ω)=(a/|a |1/2)e-jωbψˆ(a⋅ω),(17)
где s ˆ — преобразование Фурье для s ( t ).
Если C ψ = ∫ ψ ( ω ) 2 d ω / ω ограничено, то ВП имеет обратное преобразование и сигнал определяется коэффициентами w ( a , b ) по соотношению (18):
s ( t ) = (1/ C ψ ) ∫∫ w ( a , b ) ψ a , b ( t )d a d b / a 2. (18)
Важным свойством ВП является время-частотная локализация. Она определяется дисперсией времени и частоты, т. е. размером ячейки, которая служит мерой разрешающей способности преобразования. Дисперсии ∆ 2 t , ∆ 2 ω выражаются соотношениями
∆2 = 1 (t-t)2. |ψ(t) |2 dt, t ||ψ ||2
t = 1 ⋅ t ⋅ | ψ ( t ) |2 d t ;
|| ψ ||2 ∫
∆ 2 ω = 1 ⋅ ( ω - ω )2 ⋅ | ψ ˆ( ω ) |2 d ω ,
|| ψ ||2
ω = 1 ⋅ ω ⋅ | ψ ˆ( ω ) |2 d ω .
|| ψ ||2
Ячейка разрешения ВП определяется интервалом ± ∆ t и ± ∆ ω и отражает элемент разложения сигнала [13].
ВП основывается на методе анализа сигнала с различным разрешением (multiresolution analysis), называемом также кратно-масштабным анализом (КМА). Схема построения метода включает набор множеств { V j }. Проекции сигнала на них являются последовательными его аппроксимациями. Структура последовательности { V j } такова, что удовлетворяет следующим свойствам.
-
1. V j ⊂ V j +1 .
-
2. Функция v ( t ) ∈ V j ⇔ (тогда и только тогда, если) v (2 t ) ∈ V j +1 .
-
3. 3. v ( t ) ∈ V 0 ⇔ v ( t +1) ∈ V 0 .
-
4. 4. ∪ V j = L2 (L2 — множество функций (сигналов) с ∫ s 2( t )d t < ∞ ) .
-
5. ∩ V j = {0}.
-
6. Существует масштабирующая функция φ ( t ) ∈ V 0 такая, что множество ее сдвигов { φ ( t – k ), k — целое} составляет базис V 0 [20, 21].
Масштабирующая функция удовлетворяет ряду свойств, которые лежат в основе схем полосовой фильтрации, сжатия сигналов и изображений:
ϕ ( t ) = 2 ⋅ ∑ h k φ (2 t - k ), ∑ h k = 1; kk
ϕ ( t )d t = 1, ∑ ( - 1) k ⋅ h k = 0.
k
Соотношение (21) представляет уравнение растяжения [26]. Набор
{ ф jk ( t ) = 2 j /2 ^ (2 jt - k )} k = 1,2,...
является базисом для множества V j .
Частотным эквивалентом соотношения (21) служит выражение (23):
k
Применение рекурсии к выражению для ф ( ш ) в (23) приводит его к виду (24):
∞ ф (to) = п H (2j • to), H (0) = 1. (24) j=1
Кроме масштабирующей функции в алгоритмах разложения и реконструкции участвует вейвлет-функция y (t) и базис { ^ j k ( t )} для W j на ее основе. Имеет место ортогональное разложение (25), (26).Функции { ^ ( t - k )} k = 1,2,... являются базисом в W 0, а { V jk ( t ), j , k — целые} базисом в L2 [20, 23,
24, 28]:
Vj+1 = Vj® Wj,(25)
U ®Wj = L2.(26)
Вейвлет-функция ^(t) удовлетворяет соотношениям (27)-(29), по структуре аналогичным выражениям (21)-(23):
^(t) = 2 Уgk^(2t - k),(27)
k
^(to) = G (toZ2^(to/2),(28)
G (to/2) = У gke j/2.(29)
k
Выполнение преобразования удобно при ортогональном базисе. В КМА это обеспечивается выполнением соотношений (30):
(Wj! Vj) с Vj+1, Wj® Vj, j * k.(30)
Проекции Q j сигнала на { W j } образуют ортогональное разложение
^ (t) = У {Qj[ s (t)]}.
Для ортогональности КМА достаточно условия (32) или эквивалентного ему условия (33) в частотной области [15, 29]:
Wо! Vо <^(t),ф(t - 1)) = 0,(32)
У ./(to - 2nk )ф^ + 2nk) = 0.(33)
k
Для масштабирующей функции условия ортогональности выражаются соотношениями
( ф ( t ), ф ( t - k ) ) = 8 k ,0 , ^Wto + 2 n k )|2 = 1. (34) k
Условие ортогональности в частотной области для фильтра, реализующего ВП, имеет вид
У hkhk _ 2 m = (1/2) 5 m ,0 , k (35)
| H ( to ) |2 + I H( to + n ) |2 = 1, V to .
Условие ортогональности КМА накладывает на вейвлет-функцию, которая определяет базис в W 0 , следующее условие [21]:
ф ( t ), ф ( t - k ) > = 8 k ,0 ,
У | ^( to + 2 n k )|2 = 1. (36)
k
Фильтр G ( ю ), выделяющий при ВП разницу в аппроксимациях сигнала на двух уровнях масштаба, удовлетворяет условию
| G ( to )|2 + | G( to + п )|2 = 1. (37)
Получение аппроксимации сигнала и деталей (неучтенного остатка аппроксимации) реализуют операторы P j , Q j проектирования сигнала на V j и W j . В силу ортогональности базисных функций Ф j k в V j и Y jk в W j имеются разложения (38):
P j [ s ( t )] = У < s , ф у^ )ф ^ , k (38)
Q j [ s ( t )] = У < s , W J k >¥ jk .
k
Лучшая разрешающая способность КМА достигается для базисных функций с наиболее компактным носителем [19]. В этом случае (38) имеет небольшое число членов. Показано, что ортогональные вейвлет-функции получаются из масштабирующей функции при использовании зеркального фильтра:
g k = ( - 1) kh 1 - k . (39)
В том случае, если масштабирующие функции { ф ( t - k )} образуют только неортогональный базис в V 0 (базис Рисса), то его можно ортонормировать, используя преобразование (40) в частотной области [15]:
< Р орт ( to ) = < p( to )/[ F( to )]1/2; F( to ) = У | ^( to + 2 k n ) |2 . k
Совместные свойства симметрии, компактно- сти, ортогональности и гладкости базиса могут быть получены только при биортогональном вейв-лет-преобразовании (БВП). БВП построено на паре дуальных масштабирующих (ф(t), ф~(t)) и вейв-лет-функций (v(t),V(t)). Дуальные наборы подмножеств КМА удовлетворяют условиям (41), а для функций ф(t), ф(t) и v(t), 1~(t) выполняются соотношения биортогональности (42):
V j L W j , V j L W j , W j L W j .; (41)
<
Ф
,
У
(о
-
k )
} = {W, ф
(
о
-
k
)
) =
0,
Ф ф
(о
-
k
)
) =
5
k
o
,
Эти же условия в частотной области представляются в виде соотношений
У 1 ~( m + 2 ^ k ) ф *( m + 2 п . k ) = 0, k
У ф! m + 2nk )^*(m + 2nk) = 0; k
^ ф ( ш + 2 n k ) ф ) * ( ш + 2 n k ) = 1,
* - (44)
^ ~ ( m + 2. k ) у л ( m + 2 n k ) = 1. k
Биортогональные фильтры H ( to ) и G ( to ) в частотной области определяются на основе дуальных для них фильтров H ( to ) и G ( to ) по соотношениям [7]
H(m)=Gm+nl, Gm)=-H (m+п’,
A ( m ) A ( m )
где
A ( to ) = det M ( to ),
M ( m )
H ( m ) H ( m + n ) G ( m ) G ( m + n )
Разложение сигнала при биортогональном вейвлет-преобразовании производится методом перекрестного использования взаимно дуальных базисных функций: коэффициенты разложения определяются по одной из них, а восстановление сигнала s (t) = ^< s V~ у > Xj^tj (t)
или s ( t ) ^< s , ф j > ~ j ( t )
i j
представляется по другой — биортогональной ей системе базисных функций. Так что имеется два вида представления сигнала. Для коэффициентов фильтров, биортогональных относительно фильтров, определяемых наборами {hi} t = 1,2,_ и {gk } t = 1, 2,_, справедливы соотношения hk-2 j =< ф(t - j), Ф(2t - k) >, ~ k-2 j =<>~( t- jXv(2 t- k )Y
Совокупность фильтров { h i }, { gk } и { h i },{ gk } лежит в основе алгоритмов реализации биортого-нального вейвлет-преобразования речевого сигнала.
Основные итоги проведенного анализа принципов построения время-масштабного (вейвлет-) преобразования можно сформулировать следующим образом.
Вейвлет-преобразование (ВП) имеет развитую структуру математической формализации и различные формы выражения двух основных функций (масштабирующей, или скейлинг-функции, и вейвлет-функции), которые определяют базис ВП и его виды. В основе построения и использования ВП лежит кратно-масштабный анализ, в конечном счете определяющий алгоритмы вейвлет-преобразования. Кратно-масштабный анализ порождает ортогональные и биортогональные формы ВП. При этом биортогональность обеспечивает симметрию базиса ВП и, следовательно, свойство линейно-фазовости преобразования. Анализ двух методов описания ВП — на основе базисов и на основе фреймов — показал, что метод фреймов приспособлен для теоретических исследований, а для практической реализации алгоритмов ВП в прикладных исследованиях информационно-измерительных систем следует использовать базисы.
ВИДЫ БАЗИСОВ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ
Вейвлет-преобразование (ВП) имеет ряд модификаций. В основном они определяются различием базисов, от свойств которых зависят характеристики ВП. При обработке многих видов сигналов (например, речевых сигналов и сигналов, характеризующих структуру гетерогенного потока) значимыми являются свойства ВП, которые могут обеспечить быстрый алгоритм, сжатие информации, полное восстановление сигнала (при обратном преобразовании), сохранение фазового соотношения частотных компонент, гладкость. Универсальное ранжирование базисов и свойств ВП по предпочтительности невозможно. Поэтому целесообразно найти виды ВП, адекватные задачам исследования.
Свойства базиса ВП отражаются на виде алгоритма преобразования различным образом. Ортогональность дает удобство вычисления коэффици- ентов разложения и минимальное отличие фильтров анализа и синтеза, что уменьшает объем вычислений [21]. Нулевые моменты базисных функций способствуют сжатию информации при вейв-лет-представлении сигнала [30]. Компактность обеспечивает малую длину фильтров, реализующих ВП, гладкость гарантирует отсутствие искажений при ВП гладких сигналов [31–34]. Симметрия соответствует сохранению фазовых соотношений при реконструкции сигнала [33].
Некоторые сочетания свойств не могут быть у ВП одновременно. Ортогональность, компактность и симметрия у вещественного ВП реализуются только в базисе Хаара, который непригоден из-за отсутствия гладкости. При этом доказано, что для других базисов эти свойства несовместимы [7]. Поэтому особенности и структура анализируемого сигнала требуют компромисса между набором хороших свойств базиса и адекватностью выбора базиса для решаемой задачи.
Таким образом, для выбора базиса вейвлет-преобразования, соответствующего задачам исследований, требуется достаточно полно рассмотреть совокупность видов ВП и их характеристик.
Выбор вида ВП, а фактически базиса, может облегчить систематизация его характеристик. Для этой цели классифицированы 12 типов базисов по 8 признакам, включающим ортогональность (или биортогональность), компактность носителя, наличие симметрии, возможность задавать желаемое количество нулевых моментов, полноту восстановления сигнала при обратном преобразовании, регулярность — принадлежность определенному классу гладкости С n , наличие КИХ-фильтра в алгоритмах анализа и синтеза и наличие явного выражения функций ϕ ( t ) и ψ ( t ) , образующих базис. Перечень основных типов базисов и наличие (или примерное наличие ≈) перечисленных свойств даны в таблице. Краткая характеристика отдельных типов базисов дополнена сводкой основных соотношений для вейвлет-преобразований, которая приведена в приложении (ссылка на них в тексте имеет перед порядковым номером букву П).
Базис Мейера
Это базис ортонормальный, с хорошей локализацией по частоте и с высокой степенью гладкости ( ψ ( t ) ∈ C k для любого k ) . Вейвлет-функция плохо локализована во временнóй области и имеет низкое временнóе разрешение. Принцип построения базиса Мейера дан соотношениями (П1) в приложении.
Базис Морлета
Базис Морлета [34] (один из первых) построен как модулированный гауссиан. Его вещественная часть — четная положительная функция (см. (П2)
в приложении). Масштабирующая функция у вейвлета Морлета отсутствует.
Мексиканская шляпа
Вейвлет-функция — четная, вещественная. Введена Габором как вторая производная от гауссиана. Аналитическое выражение определяется выражениями (П3).
Базисы Добеши
Это — ортогональные базисы, имеют компактный носитель и ограниченную гладкость. Их свойства определяются параметром N ( N — индекс базиса db N ). N равно количеству нулевых моментов у функции ψ ( t ) , образующей базис ( ∫ t k ψ ( t )d t = 0, k = 0,1,..., N - 1) . N определяет степень компактности и гладкость базиса: область определения (носитель) ϕ ( t ) и ψ ( t ) — интервал длины 2 N – 1, их гладкость равна 0.2 N , т. е. ϕ ( t ) , ψ ( t ) ∈ C0.2 N и имеют Ent(0.2 N ) непрерывных производных. Фильтры анализа ВП { h n },{ g n } имеют длину 2 N (то же относится к фильтрам синтеза). Базис несимметричный, не слишком гладкий, т. к. только при N ≥ 5 достигается непрерывность первой производной ϕ ( t ) и ψ ( t ). Наличие N нулевых моментов обеспечивает аппроксимацию без ошибок полиномов до ( N – 1) порядка или полиномиальной компоненты анализируемого сигнала. При больших N это соответствует экономичному представлению сигнала и сжатию информации ВП.
Базис Добеши не имеет явного аналитического представления и определяется итеративным методом на ЭВМ на основе уравнений связи масштабов (П4)–(П6). Фильтры анализа { hn },{ gn } для реализации ВП Добеши методом двухканального банка фильтров получены в [19].
Сплайновые вейвлеты
Вейвлет-базис называется полуортогональным, если для любого j уровня масштаба пространство W j ортогонально V j , однако базисы их могут быть неортогональны. Отсутствие требования полной ортогональности позволяет строить гладкие симметричные вейвлеты с компактным носителем. На этом виде базиса построены сплайновые вейвлеты [35–40]. Базис состоит из В-сплайнов m -порядка (с целочисленными узлами), которые образуют масштабирующие функции, и из кардинальных сплайнов (линейных комбинаций В-сплайнов со специальным выбором коэффициентов), из которых вейвлет-функции получаются дифференцированием.
Классификация вейвлет-базисов
|
Тип базиса |
Явное выражение |
Ортогональ-ность |
Компакт-ность |
Симмет-рич-ность |
Нулевые моменты |
Регу-ляр-ность |
Полное восста-нов-ление |
КИХ-фильтр |
|
Мейера |
+ |
+ |
+ |
+ |
||||
|
Морлета |
+ |
+ |
+ |
|||||
|
Мексиканская шляпа |
+ |
+ |
+ |
|||||
|
Добеши |
+ |
+ |
+ |
+ |
+ |
+ |
||
|
В-сплайны Чу и Ванга |
+ |
+ |
+ |
+ |
+ |
≈ |
||
|
Хаара |
+ |
+ |
+ |
+ |
+ |
+ |
||
|
Койфлет (Койфлет До-беши) |
+ |
+ |
≈ |
+ |
+ |
+ |
+ |
|
|
Биортогональ-ный Добеши |
+ |
+ |
+ |
+ |
+ |
+ |
||
|
Вальтера и Цханга |
+ |
+ |
≈ |
+ |
+ |
+ |
+ |
≈ |
|
Вильсона (двухмодальный) |
+ |
+ |
+ |
+ |
+ |
+ |
≈ |
|
|
Баттла—Лама-ри |
+ |
+ |
+ |
+ |
||||
|
Симлет |
+ |
+ |
= |
+ |
+ |
+ |
+ |
В-сплайны т- порядка N т ( t ) получаются итеративно из сплайнов ( т - 1)-порядка N т- i ( t ) путем свертки с N 1 ( t ) (П7) и удовлетворяют требованиям кратно-масштабного анализа. Поэтому они используются в качестве масштабирующих функций Ф = N т ( t ). Вейвлет-функция ^ ( t ) формируется т -кратным дифференцированием кардинального сплайна L2 т ( t ): ^ ( t ) = ^ " 2(2 t - 1). А сам кардинальный сплайн представляется линейной комбинацией В-сплайнов (49):
L2т (t) фЛт (t + " — i), (49) i где ai определяется из условия L2т (к) = 8k 0, к — целое, 8 — символ Кронекера.
Математические преобразования, определяющие схему алгоритма определения вейвлет-функции и фильтров вейвлет-преобразования с базисом сплайнов, показаны выражениями (П10)-(П14).
Базис Хаара
Простейшей разновидностью базиса сплайнов нулевого порядка является базис Хаара. Он компактен, симметричен, ортогонален. Спектр вейв-лет-функции ^ ( t ) медленно убывает с частотой (как ~1/ го ). Поэтому преобразование с базисом
Хаара дает плохое разрешение по частоте. Масштабирующая функция равна индикатору интервала [0, 1]. Базовые функции ф (t ) и ш ( t ) имеют минимальную гладкость, принадлежат пространству С0(К) и, следовательно, непрерывны только сами, но не их производные. Форма описания базиса Хаара представлена соотношениями (П15).
Койфлеты
Так названы вейвлеты, построенные на основе условий Койфмана [19], исходя из требований кратномасштабного анализа, ортогональности, компактности носителя (области определения) и равного числа нулевых моментов для базовой вейвлет-функции и масштабирующей функции — для ^ ( t ) и ф ( t ):
J tk ф ( t )d t = 0, k = 0,..., L - 1; (50) J ш ( t )d t = 1, J tk ^ ( t )d t = 0, k = 1,..., L - 1. (51)
В этом случае L считается порядком системы койфлет. В [15] и [19] условия (50), (51) преобразованы в условия для функции m0( f ) (преобразования Фурье для фильтра { h 1 , h 2,...}), определены койфлеты для L = 2,.. .,10 и коэффициенты фильтра { h 1 , h 2,...}. Степень симметрии и линейность фазы возрастают с увеличением порядка койфлета.
Биортогональный базис
Симметричный биортогональный базис введен, чтобы совместить полезные свойства симметрии и полного восстановления сигнала по его вейвлет-преобразованию. Эти свойства несовместимы для ортогонального базиса, у которого фильтры анализа и синтеза едины и имеют конечную импульсную характеристику (КИХ-фильтры). Биортогональность основана на двух дуальных базисах (П16), (П17) и двух парах фильтров. Каждому из дуальных базисов соответствует своя система множеств { V j } и {V j }, удовлетворяющая условиям кратномасштабного анализа (формулы (41), (42)). Для фильтров анализа и синтеза биортогональность соответствует условиям, аналогичным условиям ортогонального КМА, но в соотношения входят пары компонент дуальных фильтров (см. (П18)-(П20)). Представление дуальных базовых функциях в частотной области выражается согласно (П21).
Биортогональность соответствует взаимной ортогональности (52), (53) для дуальных базисов, основанных на парах основных функций ф (t ) ш ( t ) и Ф ( t Ш t ) :
Ш Ш'*^ 8 У8 kk ', (52)
Ф 0 k , P 0 ' k ,> = 8 kk- (53)
Поэтому биортогональное разложение речевого сигнала выражается альтернативно по одному из дуальных базисов в виде f (t) = X( f, Ш№ W^, j, k f (t) = x< f ,Ш jk Шк. j, k
Метод преобразования с биортогональным базисом реализуется на основе квадратурных зеркальных фильтров [24, 31, 32, 41, 42]. Для полного восстановления сигнала необходимо, чтобы модуль передаточной функции T ( го ) звена анализа— синтеза c биортогональными фильтрами Н ( го ) и Н( го ) был равен единице: | T( го ) | = = | Н( го ) Н( го ) - Н( го + п ) Н( го + п ) | = 1. При получении биортогонального базиса определение фильтра основано на требовании симметрии и достаточной гладкости на границе полосы. (В этом случае п является нулем определенного порядка: Н ( п ) = 0 для частоты, равной половине частоты дискретизации сигнала). Симметричный фильтр нечетной длины L представляется полиномом от cos( го )
L - 1
Н ( го ) = £ he п = n = 01
= e M f h M + 2 MM - h cos(( M - n) го )
( n = 0 J
L = 2 M + 1.
Если кратность нуля H ( п ) = 0 фильтра равна l , то Н ( го ) можно представить в виде
Н (го) = (1 + e) lQ 0(го) = f f го cosl Т
I V 2
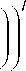
Q( го )•
Для симметрии базиса и фильтра нужно иметь зависимость от cos( го ), что возможно при четном l . Другими словами, кратность нуля должна быть четной. Если для Н ( го ) и Н( го ) выполняются условия l = 2 k и l = 2 k , то их можно представить в виде | Н( го ) | = (1 + cos го ) kQ (cos го ) и | Н( го ) | = (1 + cos го ) kQ ~(cos го ), где Q (cos го ) и Q (cos го ) — полиномы от cos( гo ).
Подстановка этих выражений в условие полного восстановления позволяет найти выражение
Н ( го ) Н ( го ) =
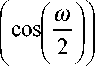
2( k + к ) m - 1
X n=0
f m
V
1 + n A
n
/
sin2 n
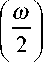
Варианты выделения двух множителей из этого выражения (факторизация) позволяют находить фильтры H ( го ) и H( to ) и определяемое ими био-ртогональное преобразование.
Значения базисных функций ф ( t ), ^ (t ) и им дуальных функций могут быть найдены как быстро сходящиеся произведения функций m( to ), m( to ) (П21) по методу [7].
Вейвлет-базис Вальтера
Особое место в системе базисов занимают конструкции с явным выражением образующих функций ф ( t ), < Х t ) и фильтров { h n }, { g n }, которые используются в алгоритме квадратурных зеркальных фильтров анализа и синтеза сигнала. Помимо простейших — базисов Хаара ( ^ ( t ) = х [0,1] ( t )), Шеннона ( ф ( t ) = sinc( t )), — а также выше описанных вариантов базисов с явным выражением (Мейера, Морлета, Мексиканская шляпа) и базисов сплайнов Чу и Ванга [35–38], к этой категории относится базис Вальтера и двухмодальный базис Вильсона.
Формирование вейвлет-базиса Вальтера [43] использует два метода:
— Метод h -функции, выбор которой обеспечивает гладкость масштабирующей функции в частотной области ф ( со ) и ее выражение через базовую h -функцию: (П22), (П23).
— Метод, использующий форму импульса с приподнятым косинусным спектром (ПКС) (который принят в кодировании для подавления межсимвольной интерференции). По этому методу получены два вида масштабирующих функций и фильтров, формирующих вейвлет-базис, один из которых приведен в соответствующем пункте приложения (П24).
Математическая схема алгоритма получения базовых функций и коэффициентов фильтров представлена выражениями (П25)–(П28).
Базис Вильсона
Вейвлет-преобразование с базисом Вильсона основано на двухмодальном варианте функции, образующей базис [44]. Эта функция f(t) для различных масштабов формируется в частотной области из функции ф(to) с хорошей локализацией по частоте и времени. Принцип формирования базиса Вильсона и алгоритм получения функции, образующей базис Вильсона, основанный на использовании преобразования Зака, дан выражениями (П29)–(П30). После перехода во временнýю область (обратным преобразованием Фурье) сдвиги по времени функции f(t) (П29) образуют вейвлет-базис.
ЗАКЛЮЧЕНИЕ
В качестве краткого заключения проведенного анализа принципов построения, структуры, типов и свойств класса время-масштабных (вейвлет-) преобразований можно сделать некоторые общие выводы.
— Существует достаточное разнообразие базисов и свойств вейвлет-преобразования (ВП), включающее наличие видов ВП с хорошей локализацией во временнóй и в частотной областях, возможность выбора симметричных базисов и использование быстрых алгоритмов. Это позволяет выбрать вид ВП, наиболее соответствующий задачам исследования.
— Желательные свойства: отсутствие искажений при восстановлении сигнала, экономное его представление со сжатием информации, сохранение фазовых соотношений частотных компонент, наличие быстрого алгоритма — соответствуют требованиям к базису ВП, которые включают компактность, гладкость (наличие нулевых моментов), симметрию.
— В наиболее развитой системе ВП Добеши нет симметричных базисов, повышение гладкости связано с ростом индекса базиса и длительности базисных функций, а как следствие, с ухудшением разрешения по времени. Вейвлеты на основе сплайнов имеют достаточно сложные алгоритмы реализации и неполную симметрию, а найденные фильтры ВП находятся в пока недоступных зарубежных работах.
— Требованиям исследования, в котором необходимо наряду с другими свойствами получить полное сохранение фазовых соотношений частотных компонент в восстановленном после преобразования сигнале, наиболее соответствуют биорто-гональные вейвлет-преобразования с базисами bior3.9 и bior6.8 [6, 15], имеющие симметрию, гладкость до первой производной, быстрые алгоритмы и систематизированные КИХ-фильтры для реализации вейвлет-преобразования.
ПРИЛОЖЕНИЕ . Основные соотношения, определяющие свойства базисов вейвлет-преобразований
Вейвлет Мейера те
V ( t ) = 2 j sin[ Q ( v )]cos[2 ^ ( t - 1/2) v ]d v ,
V ( v ) = exp( j nv )sin[ Q ( v )],
(П1)
где Q( v ) — четная, симметричная при v = 1/2 функция:
Q (1 - v ) = n /2 -Q ( v ) при 1/3 < v < 2/3, Q (1/2) = n /4.
Вейвлет Морлета
V ( t ) = exp( j to о t )exp( - t 2 /2),
V ( to ) = 2 n - exp
-
( to - to o )2
+ exp
-
( to + to 0)2
.
(П2)
Масштабирующая функция отсутствует.
Вейвлет Мексиканская шляпа
V ( t ) = (1 - 1 t 12 exp( - 1 t 12 /2), V to ) = to 2 exp( -to 2 /2).
Масштабирующая функция отсутствует.
(П3)
Базисы Добеши
Уравнения связи масштабов
^ ( t ) = X h M 2t - k ), v ( t ) = X g M 2t - k ).
kk
Частотная форма представления ^ (t ), v ( t )
( E V( EA „ ( E \.( E
Я ’( ^ ) = m о 1 1 ^ I 2 I , V ( E ) = m i l- V ^ I 2
(П4)
(П5)
где m 0 ( ξ ) и m 1 ( ξ ) — преобразования Фурье фильтров { h 1 , h 2 , … }, { g 1 , g 2, … }:
m 0 ( E ) = X hne ~jEn ,
0 2 n n
m i ( E ) = 4= X gne-jE n .
1 2 n n
(П6)
Базисы сплайны
Сплайн-функции m-порядка N m
N m ( t ) = (N m - 1 * N 1 )( t ) = j N m - 1 ( t - Z )N 1 ( Z )d Z ),
N 1 ( t ) = Z [0,1] ( t ) ^ N m ( t ) = j N m - 1 ( y )d y .
t - 1
Масштабирующая функция на основе m-сплайна
^ ( t ) = N m ( t ).
(П7)
(П8)
Кардинальный сплайн
L 2 m ( t ) = 5 a j N m ( t + m - j )•
(П9)
Значения a j определяются из условия L2 m ( t ) = 5 k 0.
Определение вспомогательных функций A ( z ) и Q ( z ) и производство замены
I to I z ^ exp l — I :
I 2 J
m
A ( z ) = 5 a j z j , Q ( z ) = l- m -P a ( z ). j z
(П10)
Определение частотной формы вейвлет-функции y /( rn ) v <( « ) = 1 Q (exp( j rn /2))^^ | ^2 J .
(П11)
Базисная функция щ (t ) получается обратным преобразованием Фурье.
Определение фильтров вейвлет-преобразования с базисом сплайнов
Из представления полиномов Эйлера—Фобениуса П ( z ) и A ( z2 )
те
П ( z ) = П 2 m - 1 ( z ) = (1 - z )2 m 5 ( j + 1)2 m - 1 z j ,
(П12)
j = 0
A(z2) = 5 ajz2 j определяются вспомогательные функции G(z) и H(z) (П13):
H ( z ) =
1 (1 - z ) m П ( z )
(2 m - 1)!2 m
2 m - 1 z
A( z 2 ) =
1 (1 - z ) m П ( z )
(2 m - 1)!2 m
2 m - 1 z
5a,z1'- j
G ( z ) =
- 1
(1 - z ) m П ( z ) П ( - z )
[(2 m - 1)!]222 m - 1
- 1
2 m - 1 z
A( z 2 ) =
(П13)
(1 - z ) m П ( z ) П ( - z )
[(2 m - 1)!]222 m - 1
Коэффициенты в представлении G ( z ) лет-преобразования:
H ( z ) = 5 h n z - n ,
n
2 m - 1 z
5 “'j j
•
и
H ( z ) по степеням z являются коэффициентами фильтров вейв-
G ( z ) = 5 g n z - n .
n
(П14)
Базис Хаара
щ ( t ) = rect[2( t - 1/4)] - rect[2( t - 3/4)],
Щ ( ю ) = 4 j
1 m
1 - cos —
to
e"j m /2
,
^ ( t ) = rect( t - 1/2), где rect( t - 1/2) = 1
при t e [0,1].
(П15)
Биортогональный базис
Биортогональные вейвлет- и масштабирующая функции
(П16)
Ф (t X Щ ( t ) ^ { ^ jk ( t )L { ^ jk ( t )};
ф ( t), V ( t ) ^ { V jk ( t )}, V , ( t )}.
Фильтры анализа и синтеза
{ h 1, h 2,..., hn ,...}, { g 1, g 2,..., gn ,...},
{ h 1 , h 2 ,..., h n ,...}, { g ~ 1 , g ~ 2 ,..., g ~ n ,...}.
Соотношения биортогональности для фильтров
S KK - 2 k = 8 k 0 , g n = ( - 1) n ■ h - n + 1, ~ n = ( - 1) n + 1 h - n + 1 .
n
Представление в частотной области дуальных базовых функций
A
<~ - ) = m0
I V I I I ’ v ( - ) = m 1
f - V f - ) , I 2 JI 2 J
m ~0, m ~1 составляются по правилу базиса Добеши из коэффициентов фильтров.
Базис Вальтера h - метод
h ( to ) > 0, to e [ - n / 3, n / 3],
n /3
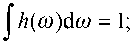
- p /3
to + n
I ф > )|2 - J h - )d - ф ( t ) = (БПФ) "»)].
- to - n
Компактность и гладкость базиса определяется выбором h- функции.
Метод импульса с приподнятым косинусным спектром (ПКС)
1 при 0 < to < n (1 - в ),
A x пкс
0"5 ' 1 + cos 2 в(l to 1 - n (1 - в )
0 при п (1 + в ) < to ;
I V ( to )|2 - x пкс ( to );
при п (1 - в ) < to < п (1 + в ),
( ) _ sin п (1 - в ) t + 4 в t • cos п (1 + в ) t .
ф (° " n t (1 - (4 в t )2) ;
4 <( to ) _ exp( - j to /2)[ V ( to + 2 п ) + q )( to - 2 n )]< p ( to /2);
V ( t + 1/2) _
[sin n (1 + в ) t - 4 в t cos n (1 - в )] n t ((4 в t )2 - 1)
sin 2(1 - в ) t + 8 в t cos 2 n ( в + 1) t n t [(8 в t ) 2 - 1]
(П17)
(П18)
(П19)
(П20)
(П21)
(П22)
(П23)
(П24)
(П25)
(П26)
(П27)
ФНЧ { h n }: h n
2 nn
—] sin л (1 - P )- + 2 P n cos n (1 + p )- mi [1 - (2 вп )2] I 2 2
.
(П28)
Базис Вильсона
Принцип формирования
¥ mn ( t ) = f m ( t - n ),
где : f m ( t ) = (БПФ) - 1[ f m ( to )],
f , ( to ) = Oto );
К ( to™ ) = ^[ ф ( to - п ) + ( - 1) k ф ( to + п )]exp( j n k to ), V 2
k = 0,1;
(П29)
Условия на ф : ф ( to ) < С (1 + to |) 1 b ; 2 ф ( to + k ) ф ( to + k + j ) = 8 j 0.
k
Алгоритм получения функции, образующей базис Вильсона, посредством ВЧП Зака
1) Задается базовая функция g ( t ) с локализацией по времени и частоте
g ( t ) < C i e
'я м, g ( to ) < C 2 e - ^tol
-
и выполняется преобразование Зака от g ( t ) — Z g ( t , ω ).
-
2) Вычисляется преобразование Зака от ф — Z ф ( t , to )
и определяется ф ( to ) как обращение этого преобразования:
Z ( t , to )
Z. (t, to) = V2----------—^2---2, ф |Zg (t, to )|2 +|Zg (t, to + 1/2)|2
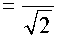
ф ( to ) J Z ф
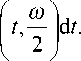
(П30)
Список литературы Классы преобразований нестационарного сигнала в информационно-измерительных системах. III. Время-масштабные (вейвлет-) преобразования для спектрально-временного анализа
- Меркушева А.В. Классы преобразований нестационарного сигнала в информационно-измерительных системах. II. Время-частотные преобразования//Научное приборостроение. 2002. Т. 12, № 2. С. 59-70.
- Duffin R.J., Schaeffer A.C. A Class of Nonparametric Fourier Series//Transactions of American Mathematical Society. 1952. V. 72. P. 341.
- Pei S.-Ch., Yeh M.-H. An Introduction to Discrete Finite Frames//IEEE Signal Processing Magazine. 1997. V. 14, N 6. P. 84-96.
- Zibulski M., Zeevi Y.Y. Oversampling in the Gabor Scheme//IEEE Transactions on Signal Processing. 1993. V. 41, N 8. P. 2679-2687.
- Oppenheim A.N., Lim J.S. Importance of Phase in Signals//Proceedings of IEEE. 1981. V. 69, N 5. P. 529-541.
- Cohen A., Daubechies I., Feauveau J.C. Biorthogonal Bases of Compactly Supported Wavelets//Communications on Pure and Applied Mathematics. 1992. V. 45. P. 485.
- Daubechies I. Painless Nonorthogonal Expansions//Journal of Mathematical. Physics. 1986. V. 27. P. 1271-1283.
- Morris J.M., Lu Y. Generalized Gabor Expansion of Discrete-Time Signal via Biorthogonal-Like Sequences//IEEE Transactions on Signal Processing. 1996. V. 44, N 6. P. 1378-1391.
- Bastiaans M.J. Decomposition of Signals in Gabor Series of Elementary Gaussian Signals//Proceedings of IEEE. 1980. V. 68, N 4. P. 123.
- Quian S., Chen D. Optimal Biorthogonal Functions for Window in Gabor Time-Frequency Analysis//IEEE Transactions on Signal Processing. 1994. V. 42, N 3. P. 694-697.
- Hess-Nielsen N., Vickerhauser M.V. Wavelets and Time-Frequency Analysis//Proceedings of IEEE. 1996. V. 84, N 4. P. 523-540.
- Kelly S., Kon M. Pointwise Convergence of Wavelet Expansions.//Bull. American Mathematical Society. 1994. V. 29. P. 87-94.
- Mallat S.G. Multifrequency Chanel Decompositions of Image and Wavelet Models//IEEE Transactions on Acoustic, Speech and Signal Processing. 1989. V. 37, N 12. P. 2091-2110.
- Rioul O., Vetterli M. Wavelet and Signal Processing//Signal Processing Technology and Applications./Ed. Ackenhausen J.G. IEEE Press, 1995.
- Daubechies I. Ten Lectures on Wavelets//Conference Board of Mathematical Sciences. Society of Industrial and Applied Mathematics (SIAM), 1991. P. 258.
- Morris J.M., Lu Y. Discrete Gabor Expansion of Discrete-Time Signal via Frame Theory//Signal Processing. 1994. V. 40, N 2, 3. P.155-181.
- Qian S., Chen D. Discrete Gabor Transform//IEEE Transactions on Signal Processing. 1993. V. 41, N 7. P. 2429-2438.
- Zibulski M., Zeevi Y. Frame Analysis of Discrete Gabor Scheme//IEEE Transactions on Signal Processing. 1994. V. 42, N 4. P. 942-945.
- Daubechies I. Orthogonal Bases of Compactly Supported Wavelets//Communications in Pure and Applied Mathematics. 1988. V. 41, N 7. P. 909-996.
- Daubechies I. Orthogonal Basis and Wavelets//SIAM Journal of Mathematical Analysis. 1993. V. 24, N 2. P. 499.
- Daubechies I. Wavelet Transforms and Orthogonal Wavelet Bases//Proceedings of Symposia in Applied Mathematics. 1993. V. 47. P. 1-32.
- Heil G.E., Walnut D.F. Continuous and Discrete Wavelet Transforms//SIAM Review. 1989. V. 31, N 12. P. 628.
- Mallat S.G. A Theory for Multiresolution Signal Decomposition: the Wavelet Representation//IEEE Transactions on Pattern Analysis and Machine Intelligence. 1989. V. 11, N 7. P. 674-693.
- Mallat S.G. Multiresolution Approximations and Wavelet Orthogonal Bases in L2(R)//Transactions of American Mathematical Society. 1989. N 315. P. 69-87.
- Strang G. Wavelet Transformations and Fourier Transformations//Bull. American Mathematical Society. 1993. V. 28. P. 288-305.
- Strang G. Wavelets and Diliation Equations//SIAM Review. 1989. V. 31, N 4. P. 614.
- Cohen A., Kovacevic J. Wavelets: Mathematical Background//Proceedings of IEEE. 1996. V. 84, N 4. P. 514-522.
- Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет. Л., 1999. 203 с.
- Уидроу Б., Стирнз С. Адаптивная обработка сигналов. М.: Радио и связь, 1989. 439 с.
- Villemois L.F. Energy Moments in Time and Frequency for 2-Scale Equations and Wavelets//SIAM Journal of Mathematical Analysis. 1992. V. 23. P. 1119-1153.
- Akansu A.N., Tazebay M.V., Medley M.I., Das P.K. Wavelet and Subband Transforms: Foundations and Communication Applications//IEEE Communication Magazine. 1997. V. 35, N 12. P. 104-115.
- Kurosawa K., Jamamoto J. A Simple Design Method of Perfect Reconstruction Quadrature Mirror Filter Banks//IEEE Transactions on Circuits and Systems, II -Analog and Digital Signal Processing. 1994. V. 41, N 3. P. 243-245.
- Lee J.H., Yang S.J. Perfect Reconsruction Filter Banks Having Linear Phase//IEEE Transactions on Acoustics, Sound and Signal Processing. 1986. V. ASSP-34, N 6.
- Grossman A., Morlet J. Decompositions of Hardy Functions into Square Integrand Wavelets of Constant Shape//SIAM Journal of Mathematical Analysis. 1984. V. 15. P. 723.
- Chui Ch.K., Li C. Nonorthogonal Wavelet Packets//SIAM Journal of Mathematical Analysis. 1993. V. 24. P. 712-738.
- Chui Ch.K.//Transactions of American Mathematical Society. 1992. V. 330. P. 907-909.
- Chui Ch.K., Wang J-Z. A Cardinal Spline Approach to Wavelets//Proceedings of American Mathematical Society. 1991. V. 113, N 3. P. 785-789.
- Chui Ch.K., Wang J.Z. Compactly Supported Spline-Wavelets and Duality Principle//Transactions of American Mathematical Society. 1992. V. 330. P. 903-907.
- Unser M. A Family of Polinomial Spline Wavelet Transformations//Signal Processing. 1993. V. 30. P. 141-162.
- Unser M., Aldroubi A. Shift-Orthogonal Wavelet Basis Using Splines//IEEE Signal Processing Letters. 1996. V. 3, N 3. P. 85.
- Yang R.H., Lim Y.C. Novel Efficient Approach for the Design of Equiripple Quadrature Mirror Filters//IEE Proceedings on Vision, Image and Signal Processing. 1994. V. 141, N 2 (April). P. 95-100.
- Nemer E., Goubran R., Mahmoud S. SNR Estimation of Speech Signal Using Subbands and Forth-Order Statistics//IEEE Signal Processing Letters. 1999. V. 6, N 7. P. 171-174.
- Walter G.G. A Sampling Theorem for Wavelet Subspaces//IEEE Transactions of Information Theory. 1992. V. 38, N 2. P. 881-884.
- Daubechies I., Jaffard S., Journe J.L. A Simple Wilson Orthonormal Basis with Exponential Decay//SIAM Journal of Mathematical Analysis. 1991. V. 22, N 2. P. 554.


