Кластеризация диагностических тестов при изучении предлогов английского языка в соответствии с таксономией Блума

перечислением возможных значений с поверхностным объяснением связи между пространственным значением и непространственными расширениями [5]. Исключением данной тенденции является работа [8], которая для представления предлогов использует когнитивный подход, частично опираясь на теорию метафоры. Как отмечают авторы [5], несмотря на недостатки, связанные с отсутствием анализа концептуальной теории метафоры и полисемии, а также привязыванием метафорических значений к ряду предлогов без достаточных объяснений, использование полисемической модели [9,10] позволяет значительно улучшить подход к изучению языка.

Другая потенциальная трудность связана с тем, что однокоренные слова, принадлежащие к разным частям речи, и слова со связанными или близкими значениями зачастую требуют различных предлогов [1]. Дополнительную трудность создает также и тот факт, что наблюдаются случаи срастания предлога со связываемой им знаменательной частью речи в единое смысловое целое, например at night, angry with, look for [4]. Употребление предлога в данных сочетаниях часто немотивировано и требует механического запоминания.

Анализируя английский как иностранный, описанные трудности являются дополнением к потенциальной неопределенности, вызванной отсутствием связи между системами предлогов в родном и иностранном языках [1,5]. В частности, такие кросс-культурные вариации включают разницу в типе грамматической формы и сегментации пространственных сцен при использовании предлогов места [5]. Все это делает предлоги чрезвычайно сложными в обучении и преподавании. Учитывая сложность данного языкового явления, была поставлена задача создания адекватной модели, которая бы сформировала грамматическую основу для представления предлогов и способствовала бы его корректному выбору в новом контексте.

Одним из решений данной проблемы является применение адаптивного метода обучения, который основан на корректировке обучающего контента и способов его представления, исходя из действий обучаемого. В качестве основы предлагается использовать таксономию [11-15], созданную Б. Блумом в 1956 [11] и впоследствии доработанную Л. Андерсоном [12]. В этой теории уровни мышления описываются по возрастанию сложности задачи с помощью следующих глаголов: помнить, понимать, применять, анализировать, оценивать, создавать. Каждый уровень представляет собой набор мыслительных операций для решения определенной образовательной задачи. В этом смысле, таксономия Блума может являться основой при формировании образовательного контента, создания заданий и их оценивания. Применяя данную теорию к проблеме изучения предлогов, необходимо на каждом этапе предлагать материал, соответствующий заданному когнитивному уровню для повышения эффективности обучения.

Неотъемлемой частью адаптивного обучения является диагностическое тестирование, позволяющее оценить текущий уровень знаний в изучаемой области. Прежде чем определить стартовый уровень освоения материала, необходимо разработать банки диагностических тестов [16-19], что является трудоемкой задачей ввиду необходимости соответствия контента строго определенному когнитивному уровню, учета схожести вопросов в рамках одного банка заданий и последовательности их представления согласно таксономии. В целях упрощения данной задачи, было сделано множество попыток автоматизировать этот процесс [17-19] с помощью алгоритмов машинного обучения в рамках создания систем адаптивного обучения [20,21].

Важным аспектом, который необходимо учитывать при тестировании, является инструмент анализа, который определяет тип вопросов. В работе [21] автор указывает на «multiple choice» как на универсальный инструмент для формирования пары «вопрос-ответ» даже на высоких когнитивных уровнях. Данная точка зрения в последующем получила подтверждение в работах [22-25], однако, требует проведения дополнительного анализа случайности выбора правильных ответов с учетом психологических факторов [26-28].

Таким образом, целью данной работы является кластеризация банка диагностических тестов при изучении предлогов английского языка в соответствии с таксономией Блума.

ФОРМАЛИЗАЦИЯ ЗАДАЧИ

Анализ проведенных исследований в области адаптивного обучения показал, что существует множе ство подходов для решения поставленной задачи [2935], среди которых используются алгоритмы машинного обучения без учителя (кластеризации). Данные алгоритмы позволяют разбить множество объектов на группы схожих, сократить объем данных, оставив по одному типичному представителю, а также выделить нетипичные объекты, неподходящие ни одному из кластеров. Ввиду известного значения числа кластеров I, заданного числом когнитивных уровней таксономии, наиболее целесообразным является применение следующих методов [36-40]:

• 1)    k-means с четким разбиением на уровни;

• 2)    c-means с определением степени принадлежности через задание коэффициента нечеткости;

• 3)    иерархическая кластеризация, имитирующая структуру таксономии Блума.

Для представления методики кластеризации банка диагностических тестов в соответствии с таксономией Блума, введем ряд определений.

Определение 1. Пусть U – конечное множество ответов обучаемых, X – конечное множество когнитивных уровней. Тогда отображение x 0: U ^ X называется задачей диагностического тестирования.

Определение 2. Отображение r : U ^ D_r , где D_r = { 0,1 } , называется корректностью ответа.

Определение 3. Пусть {^m }m =1.M - M банков с N тестовых заданий qm = \t и } , „ m      m,n ^n =1. n в каждом. Тогда вектор ur =(r(q 1), ...,r(qm)) называется результатами оценки ответов и е U на вопросы q е Q.

Определение 4. Пусть q x е Q - банки тестов , соответствующие когнитивным уровням x е X .

Тогда отображение q^x : Q ^ X называется задачей кластеризации банка вопросов Q с мерой р ( и , и ') .

С учетом приведенной формализации, представим методику кластеризации банка тестов в следующем форме:

• 1)    формирование набора тестовых заданий

• 2)    задание метрического пространства в виде результатов оценки ответов U r е [ 0,1 ] в пределах одного банка на основе всей совокупности и е U ;

• 3)    выбор меры р ( и , и ') в метрическом пространстве u^r е [ 0,1 ] ;

• 4)    оценивание косинусных мер сходства векторов

( r ( t m,1 ),..., r ( t m , n )) g D_r , n = 1. N для каждого банка q m G Q с построением симметричной матрицы сходства между парами векторов через нахождение скалярного произведения r ( t_m i ) • r ( t_m j ) , i, j = 1. N ;

• 5)    реализация алгоритмов кластеризации значений u^r g [ 0,1 ] с мерой p ( u, u ').

Сформируем банки диагностических тестов

{ q_m } _m = ₁ M , где M = 9 , и зададим алгоритмы функционирования инструмента «multiple choice» для формирования вектора ( r ( t m ₁ ), ... , r ( t_{m n} )) g D r , n = 1. N для каждого банка q_m G Q в виде таблицы 1, где для компактности представления введены следующие обозначения:

L – возможное количество вариантов ответа, предоставляемых «multiple choice»;

P – множество всех предлогов;

O – множе ство всех предлогов, обладающих омонимичностью O с P ;

C – множество всех предлогов, имеющих коллокации с заданным словом C с P ;

О ф - множество всех предлогов, обладающих омонимичностью, с пространственными значениями

• ^ф : P ^ О _ф ^;

О _ф - множество всех предлогов, обладающих омонимичностью, с метафорическими значениями

Ф : P ^ ° _v

Таблица 1. Банки диагностических тестов и алгоритмы анализа ответов

	Инструкция	Алгоритм «multiple choice»
1	Choose the correct preposition in brackets, if necessary.	N = 5 , L = 3 ({ u r | u r = o } n ) , n = 1.. N , l = 1.. L
2	In the text field below, write the numbers of the sentences in which there is no preposition.	N = 5 , L = 5 ({ u r | u l = o } n ) , n = 1.. N , l = 1.. L
3	Choose appropriate prepositions from the list below to complete the sentences. in, at, on, of, on, -	N = 5 , L = 6 ({ u r | u l = 0 } n ) , l = 1.. L , n = 1.. N
4	Complete the sentences with correct prepositions if necessary or write ‘-’ instead.	N = 5 , L = |P| ({ u r | u r = 0 } n ) , n = 1.. N , l = 1.. L
5	Correct mistakes in prepositions if necessary. Write the correct preposition or ‘-’ instead.	N = 5 , L = P ({ u r | u r = 0 } n ) , n = 1.. N , l = 1.. L
6	Fill in the blanks using the best choice(s) from the suggested lists.	N = 5 , L = C ({ u r | u r = 0 } n ) , n = 1.. N , l = 1.. L
7	Reorder the sentences on your right so that they have the same preposition in each line with the sentences on the left. Write these prepositions in the text field below one by one separating them by commas.	N = 5 , L = | O| ({ u r | u r = 0 } n ) , n = 1.. N , l = 1.. L
8	What picture best describes the sentence ‘The cat jumped over the wall.’? Write the appropriate letter(s) in the text field below.	N = 4 , L = | 0 j ({ u r | u r = o } n ) , n = 1.. N , l = 1.. L
9	Read the text below. Paraphrase each preposition OVER, using a phrase or a word, which is similar in meaning. Write these phrases or words in the text field, separating them by commas.	N = 4 , L = | O y| ({ u r | u r = o } n ) , n = 1.. N , l = 1.. L

ВЫЧИСЛИТЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ

С целью проверки адекватности предложенной методики, была проведена серия вычислительных экспериментов для каждого из перечисленных выше методов кластеризации, чтобы повысить качество полученных результатов. Ниже представлен код, реализованный в пакете R.

install.packages(«e1071») install.packages(«lsa») # инициализация n<-10; N1<-5; N2<-4; t<-0:1 # моделирование ответов matrix_t1<-c(); matrix_t2<-c(); matrix_t3<-c(); matrix_t4<-c(); ma-trix_t5<-c()

matrix_t6<-c(); matrix_t7<-c(); ma- trix_t8<-c(); matrix_t9<-c()

for(i in 1:N1){ matrix_t1 <- cbind(matrix_t1, sample(t, n, replace = TRUE))

matrix_t2 <- cbind(matrix_t2, sample(t, n, replace = TRUE))

matrix_t3 <- cbind(matrix_t3, sample(t, n, replace = TRUE))

matrix_t4 <- cbind(matrix_t4, sample(t, n, replace = TRUE))

matrix_t5 <- cbind(matrix_t5, sample(t, n, replace = TRUE))

matrix_t6 <- cbind(matrix_t6, sample(t, n, replace = TRUE))

matrix_t7 <- cbind(matrix_t7, sample(t, n, replace = TRUE)) } for(i in 1:N2){ matrix_t8 <- cbind(matrix_t8, sample(t, n, replace = TRUE))

matrix_t9 <- cbind(matrix_t9, sample(t, n, replace = TRUE)) }

• #    меры сходства

t1_sim<-cosine(matrix_t1); t2_sim<-cosine(matrix_t2)

t3_sim<-cosine(matrix_t3); t4_sim<- cosine(matrix_t4)

t5_sim<-cosine(matrix_t5); t6_sim<- cosine(matrix_t6)

t7_sim<-cosine(matrix_t7); t8_ sim<-cosine(matrix_t8); t9_sim<-cosine(matrix_t9)

• #    матрица ответов в метрическом пространстве

vec_q1<-c(); vec_q2<-c(); vec_q3<-c(); vec_q4<-c(); vec_q5<-c()

vec_q6<-c(); vec_q7<-c(); vec_q8<-c(); vec_q9<-c(); matrix_q<-c()

for(i in 1:n){ vec_q1 <- c(vec_q1, sum(matrix_ t1[i,])/N1)

vec_q2 <- c(vec _q2, sum(matrix_ t2[i,])/N1) vec_q3 <- c(vec _q3, sum(matrix_ t3[i,])/N1) vec_q4 <- c(vec _q4, sum(matrix_ t4[i,])/N1) vec_q5 <- c(vec _q5, sum(matrix_ t5[i,])/N1) vec_q6 <- c(vec _q6, sum(matrix_ t6[i,])/N1) vec_q7 <- c(vec _q7, sum(matrix_ t7[i,])/N1) vec_q8 <- c(vec _q8, sum(matrix_ t8[i,])/N2) vec_q9 <- c(vec _q9, sum(matrix_ t9[i,])/N2) } matrix_q<-cbind(vec_q1,vec_q2,vec_ q3,vec_q4,vec_q5,vec_q6,vec_q7,vec_ q8,vec_q9)

• #    задание меры

dtest <-apply(dtest, 2, diff); dtest <-t(dtest)

• #    k-means

  dtest_km<- kmeans(dtest, 6, 10000); print(dtest_km)

• #    c-means

  dtest_cm<-cmeans(dtest,6,10000, verbose=TRUE,method=»cmeans»,m=6); print(dtest_cm)

• #    иерархическая кластеризация

dtest_hc <-hclust(dist(dtest)); print(dtest_hc)

plot(dtest_hc)

groups <- cutree(dtest_hc, k=6)

Приведем основные результаты проведенных экспериментов. Смоделированные ответы на тестовые вопросы в метрическом пространстве представлены в таблице 2. В таблице 3 – результаты работы алгоритмов k-means и c-means, на рисунке 1 – дендрограмма с результатами иерархической кластеризации, построенная в пакете R.

С учетом того, что порядок уровня не привязывался к заданному диагностическому банку тестовых заданий, результаты, полученные с помощью каждого из рассмотренных уровней, можно считать идентичными.

Из полученных результатов следует, что, на- пример, тестовый банк q4 выделен в отдельный кластер. Ниже представлены матрицы ответов на

⁽{ ^{Г ( t}m , n ^)} v ) , где m = ⁴, с

тестовые задания в банке

количеством испытаний v = 10, N = 5, n = 1. N, и матрица косинусных мер сходства между заданиями r(tm,i) • r(tm, j ), i, j = 1. N, соответственно:

v

	r 0	1	0	1	1 ^
	i	1	0	0	0
	0	0	1	1	0
	1	1	1	1	1
	1	0	0	1	1
) =	1	1	1	1	1	,
	1	1	0	1	1
	0	0	0	1	0
	0	0	0	0	0
	1 1	1	1	1	1 7
r	1	0,833		0,612		0,722 0,833 )
0,833		1		0,612		0,722 0,833
0,612		0,612		1		0,707 0,612
0,722		0,722		0,707		1    0,866
( 0,833		0,833		0,612		0,866     1 J

.

Таблица 2. Смоделированные ответы в метрическом пространстве

	tb1	tb2	tb3	tb4	tb5	tb6	tb7	tb8	tb9
1	0,2	0,4	0,8	0,6	1,0	0,4	0,2	0,75	0,5
2	0,4	0,4	1,0	0,4	0,4	0,4	0,4	0,5	0,25
3	0,6	0,4	0,6	0,4	0,8	0,6	0,4	0,5	0,75
4	1,0	0,6	0,6	1,0	0,4	0,6	0,2	0,25	0,5
5	0,8	0,2	0,6	0,6	0,8	0,8	0,8	0,5	0,5
6	0,6	0,4	0,6	1,0	0,2	0,4	0,6	0,0	0,25
7	0,2	0,4	0,6	0,8	0,4	0,2	0,4	0,5	0,25
8	0,4	0,8	0,4	0,2	1,0	0,6	0,6	0,5	0,5
9	0,2	0,4	0,6	0,0	0,6	0,6	0,8	1,0	1,0
10	0,6	0,2	0,6	1,0	0,8	0,2	0,6	0,5	0,25

Таблица 3. Результаты кластеризация с помощью k-means и c-means

	tb1	tb2	tb3	tb4	tb5	tb6	tb7	tb8	tb9
k-means	5	5	1	3	2	4	4	6	6
c-means	5	5	1	4	3	2	2	6	6

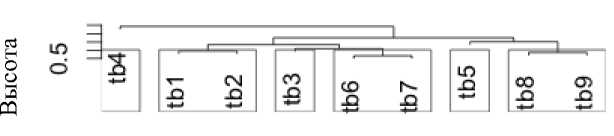
Рис. 1. Дендрограмма с иерархической кластеризацией банка диагностических тестов

Представленные значения матрицы схожести позволяют сделать вывод об аналогичности тестовых заданий, представленных в одном банке.

ВЫВОДЫ

В рамках данной работы были сформированы банки диагностических тестов при изучении предлогов английского языка и создана методика их кластеризации на основе таксономии Блума.

С целью формального описания поставленной задачи кластеризации были сформулированы определения задач классификации и кластеризации, а также корректности ответа и результата оценки ответа на заданный тестовый вопрос. Предложенные определения позволили описать структуру алгоритма «multiple choice», который, в свою очередь, формирует матрицы ответов для определения меры сходства и задания метрического пространства, необходимого для реализации алгоритмов кластеризации методами k-means, c-means и иерархической кластеризации. Серия вычислительных экспериментов подтвердила целесообразность полученных теоретических результатов и адекватность предложенной методики.

Дальнейшее направление исследований связано с проведением тестирования на совокупности обучаемых с их последующей классификацией на когнитивные уровни и с построением оптимальных обучающих траекторий с помощью деревьев решений.

ФИНАНСИРОВАНИЕ

Работа выполнена при государственной поддержке Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013-2020 годы.