Кластеризация управляемых объектов на основе сходства их траекторий и скоростных режимов

Современное развитие приборов систем теле- и видеонаблюдения, в том числе использование космических спутников, способствует накоплению огромного количества данных о траекториях перемещения различных объектов (людей, наземного, морского, воздушного транспорта, и т.п.). Классификация траекторий движущихся объектов, т.е. построение моделей для предсказания классов таких объектов (согласно их траекториям и различным дополнительным характеристикам), используется в ряде практических приложений для анализа, транспортных сетей [1, 2], создания военных систем наблюдения [3], морского пограничного контроля [4], оптимизации загруженности взлётно-посадочной полосы и обеспечения безопасности воздушного пространства в крупных аэропортах [5]. Задача кластеризации траекторий движения возникает и при управлении мультиробототехнически-ми системами. Она. обусловлена, необходимостью предсказания движения для организации взаимодействия объектов системы на. основе выделяемых паттернов в траекториях движения [6]. Кластеризация объектов робототехнических систем также упрощает контроль их согласованного перемещения [7, 8].

Для кластеризации кривых, представляющих траектории движения, применяются различные методы, из которых наиболее эффективен метод локальной полиномиальной регрессии [9]. Затем решается задача, выравнивания кривых методами динамического программирования. В настоящей работе для кластеризации траекторий движущихся объектов применяется подход, использующий полиномиальную модель, который позволяет выполнить кластеризацию и выравнивание одновременно. Анализ дополнительных характеристик, таких как скоростные режимы наблюдаемых объектов, позволяет проявить тонкую структуру кластера и оценить его однородность, т.е. отклонение кривых от тренда.

Для кластеризации траекторий при обучении полиномиальной регрессии используется итеративный алгоритм ожидания и максимизации правдоподобия (ЕМ-алгоритм) [10]. Задача выравнивания кривых с использованием модели априорных вероятностей, заданных на. множестве возможных выравниваний, решается ЕМ-алгоритмом, что формализует так называемый подход Прокруста, для анализа, кривых [11]. Априорные вероятности выравнивания интегрируются в модель смеси конечного числа, распределений, на. основе которой выполняется кластеризация.

Ранее модель смеси гауссовых распределений с обучением посредством ЕМ-алгоритма использовалась для совместной кластеризации и выравнивания при корректировке изображений, которые подвергались различным линейным преобразованиям [12]. Однако та- кая модель рассматривает преобразования в дискретном пространстве пикселей, в то время как подход, применяемый в настоящей работе, направлен на моделирование кривых и допускает произвольное и непрерывное их выравнивание в пространстве и во времени. Эффективность такого подхода демонстрируется на примере анализа данных радаров международного аэропорта г. Сан-Франциско, находящихся в свободном доступе на сайте

2.    Модель одновременной кластеризации и выравнивания одномерных временных рядов

Рассмотрим одновременную кластеризацию и выравнивание одномерных временных рядов, т.е. векторов переменной длины, представляющих координатные временные зависимости. Каждый вектор Zi G R^WiX1, г = 1, 2,..., состоит из последовательности измерений координатной зависимости Zi = Zi (t) в моментьi времени t i G R^WiX1. В [13] модели смеси регрессий эффективно используются для кластеризации одномерных векторов переменной длины. Вектор Z i моделируется регрессионной моделью

Z i = Т i 3 + E i, (1)

где 3 ~ вектор коэффициенте в регрессии размерности (q + 1) х 1 и E i — гауссов шум с нулевым средним, а Т і — регрессионная матрица. Матрица Т і зависит от типа используемой регрессионной модели. В случае полиномиальной регрессии Т і имеет вид стандартной матрицы Вандермонта:

	■ 1 ti[1]	(ti[1])2     .	.  №])9 '
Т i =	...    ... ...    ... . 1     ti[Ni]	...       . ...       . (ti[Ni])2 .	..       ... ..       ... . (ti[Ni ])9.	.                                  (2)

В основе модели одновременной кластеризации и выравнивания лежит модель смеси регрессий, в которую вводятся четыре независимых параметра преобразований выравнивания и масштабирования во времени и пространстве { Ф і } = {di, bi, Ci, di} (параметры di и bi описывают масштабирование и сдвиг во времени, а параметры Ci и di описывают масштабирование и смещение в пространстве измерений). Полиномиальная регрессия для одномерного случая имеет вид

Z i = Ci^i 3 _k + di + E i,                                     (3)

где и матрица Ті получается из Ті (4) подетановкой ti ^ dit — bi, 3k определяет модель регрессии для k-ro кластера (k = 1, А), Ei — гауссов шум с нулевым средним и дисперсией ^I. Поэтому распределение плотности условной вероятности имеет вид pk (zi|di, bi, Ci, di) — N (zi |CiTi/3k + di, CTkI).                                (4)

Плотность вероятности для кривой Z i однозначно задаётся соответствующим множеством параметров { Ф і }, которые подлежат определению. Задача кластеризации кривых решается как стандартная задача оценки скрытых данных. Каждый из параметров преобразования в (5) и (4) рассматривается как характерная для z _i случайная переменная с заранее известным распределением вероятности для кластера. Параметры преобразования и параметры модели оцениваются одновременно посредством ЕМ-алгоритма.

3.    Априорные распределения вероятностей для параметров преобразования

Априорные распределения вероятностей для параметров преобразования выбираются таким образом, чтобы тождественное преобразование являлось наиболее вероятным. С уче- том этого эффективной априорной вероятностью является гауссово распределение плотности вероятности Н(ц, с2) со средним ц и дисперсией ст2. Поэтому априорные распределения плотности вероятности для параметров преобразования времени определяются как нг -Н(1,т2), bi -Н(0, Sg),                              (5)

и априорные распределения вероятности для параметров преобразования координаты задаются как

С -Н (1,4 ), di -Н(1,^).                          (6)

В (6) параметры дисперсии п2 и -и2 зависят от кластера. Однако любое подмножество этих параметров может быть выровнено («сшито») между кластерами, если это требуется для конкретного приложения. Отметим, что априорные распределения вероятности технически допускают отрицательное масштабирование во времени и в пространстве измерений. Хотя этот результат не типичен, можно задать другие априорные распределения вероятности, например логарифмически нормальные, чтобы не допустить отрицательного масштабирования. Следует заметить, что дисперсии для параметров априорных вероятностей выводятся на основе данных, полученных в результате работы ЕМ-алгоритма. Ниже модель (5) - (6) совместной кластеризации и выравнивания кривых обобщается на случай многомерного пространства измерений.

• 4.    Кластеризация и выравнивание многомерных кривых

• 4.1.    Регрессионные модели выравнивания в многомерном пространстве

Рассмотрим выравнивание кривых в многомерном пространстве. Ранее предполагалось, что вектор Zi G R^Ntx1 состоит из последовательности измерений одномерной координатной зависимости в моменты времени t i G R^Ntx1. Однако во многих приложениях такие зависимости от времени являются многомерными. Таким образом, каждому моменту времени Zi[j]) 3 = 1,Ni, соответствует многомерный вектор D измерений. Обозначим многомерные кривые как Z i G R^NtxD, полученные в результате измерений в моменты времени t i G R^Ntx1. Тогда матрица Z i = { Д [j; Z], j = 1, Ni, I = 1, D} состоит из D столбцов, таких, что каждый Z-й столбец z^ = {Д[3; Z], j = 1,N_i}, I = 1,D, содержит последовательность измерений Z-й одномерной координатной зависимости для Тй рассматриваемой переменной. То есть столбец z ⁽\ соответствующий одномерному вектору Z i G R^Ntx1 в (3), оказывается вложенным в матрицу многомерной кривой Z i G R^NtxD.

Для многомерной кривой Z i G R^⁰ измерения каждой координаты описываются независимой регрессионной моделью:

• z^ = Т іЗ_ы + du + E i, du ^Н (0,v2) , Ei ^Н (О^хц оЦ NtxNt ) ,       (7)

где Т i — матрица Вандермонта (4). Матрица З ы задаёт коэффициенты регрессии для Z-ro измерения (т.с. коэффициенты регрессии для Z-ro столбца Z i G R^{n xD}) и d_il задаёт смещение для Z-ro измерения, 0N_{t x}i — вектор с нулевыми компонентами размерности Ni х 1 и I Nt _XNi ~ тождественная матрица размерности Ni х Ni. Использование параметров 4, н^ позволяет рассматривать дисперсию по каждому измерению независимо.

На основе модели (7) плотность вероятности многомерной кривой Z i G R ^{n xD} и D параметров смещения { du, Z = 1,D} определяется следующим образом:

D

• р ( Z i, dil, ..., diD ) = П Н (z^(l) I Т іЗы + dil, 4l I Nt xN,) Н ( dil | 0, 4l ) .         (8)

l=1

Плотность вероятности (8) учитывает два необходимых условия: во-первых, все координаты пространства кривых Zi G RNtxD и, во-вторых, предполагается, что для каждого измерения l существует собственное множество параметров смещения {Ф»}/. Далее предполагается, что эти два условия всегда выполняются.

Плотность безусловного распределения (компонента многомерной случайной величины) р (Z») представляется в виде произведения р (Z») = П р Zz^V поэтому логарифм ____)/=1

правдоподобия Z = {Z», г = 1,W} имеет вид

N           ND,х log (р (Z)) = Е 1og(р (Z»)) = ЕЕlog Г / р ( z(/) | d»^ р (du) ddu\ .

»=1                  »=1 /=1

Интегрирование в (9) может быть выполнено аналитически, что приводит к следующему виду логарифма правдоподобия:

N D

»=1 /=1

где 1NixNi ~ единичная матрица размерности N» х N».

• 4.2.    Регрессионные модели выравнивания многомерных кривых во времени

Поскольку независимые координаты многомерного пространства смещаются и масштабируются независимо, для выравнивания в пространстве рассматриваются D отдельных параметров преобразования. Однако изменение во времени каждой координаты траектории происходит в одном и том же временном масштабе, следовательно, параметры преобразования времени должны быть распределены одинаково по всем D измерениям. Поэтому каждому из векторов z^ Е R^NiX1 соответствует единственный параметр Ь». Тогда условная плотность вероятности Z » Е R^NiXD определяется как

DD

• р(Z»|ь») = Пр^^Іь») = Пw(z(/)| T^,a2/1nXN.),(11)

  /=1/=1

где используется одно Ь» для всех l = 1, D и матрица Т» получается из Т » (4) подстановкой t » ^ t » — Ь». Условная плотность вероятности разлагается на множители, а безусловная плотность вероятности р ( Z ») не разлагается, поскольку различные измерения в пространстве оказываются связанными через параметр смещения Ь». Следовательно, для логарифма правдоподобия Z = {Z », г = 1,W} имеем

N           N

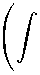
log (р (Z)) = Е log (р (Z»)) = Е log

»=1                 »=1

Под знаком интеграла в формуле (12) находится произведение вероятностей по всем измерениям пространства, что приводит к сложным вычислениям логарифмической функции правдоподобия. Однако с помощью методов Монте-Карло можно вычислить аппроксимацию этой функции следующим образом:

N     М D log (р (Z)) та Е log ( Е П р (Z»W| Ь»Н) ) — N log(M),             (!3)

»=1    \т=1 /=1

где

Ь^(т) х W (0, ту²) , ттг = 1, М.

5.    ЕМ-алгоритм

Сложность ЕМ-алгоритма, обеспечивающего одновременное обучение параметров модели и преобразования, является линейной функцией от полного числа точек N = ^2 N г многомерных траекторий Z г. Пусть тг_г — принадлежность Z г к некоторому кластеру. Параметры {Фг} и принадлежности к кластеру рассматриваются как скрытые переменные. В таком случае логарифмическая функция правдоподобия для полного набора данных определяется как совместная логарифмическая функция правдоподобия множества Z = {Z г, г = 1,N} и скрытых переменных Ф = {Фг, тт^}. Что в соответствии с формулой (11) может быть записано в виде суммы по всем N кривым логарифма от произведения а^ и совместного распределения вероятности (8), зависящего от кластера

N D

^Lc = ^^ ^log («^ Р_Ті ^(z/ ^ФЛ/Г (^фг)) .                     (15)

г=1 1=1

На Е-шаге оценивается распределение вероятности р(Фг , tt^ I Z г) и затем используется в качестве следующего ожидаемого распределения в (15). На следующей итерации это ожидаемое распределение используется на М-шаге для оценки параметров модели в p_{T i} ( z^ |Ф_г).

6.    Численный эксперимент

Описываемый в настоящей работе подход к кластеризации кривых тестируется на реальных данных радара TRACON (Terminal Radar Approach Control), регистрирующего траектории полётов воздушных судов над заливом Сан-Франциско (данные находятся в открытом доступе на сайте . Рассматривается область воздушного пространства над тремя крупными аэропортами: Окленда, Сан-Франциско и Сан-Хосе (Oakland, San Francisco and San Jose International Airports). Это пространство ограничивается цилиндром радиуса 80 км с центром над аэропортом Окленда и высотой б км. Данные содержат трехмерные координаты и абсолютные скорости воздушных судов с момента обнаружения радаром и до самой нижней регистрируемой радарами высоты. Помимо основной информации в записях указываются дополнительные сведения о типе совершаемой операции (прибытии или отправлении), о пункте вылета и назначения и др. В настоящей работе анализируются траектории и скоростные режимы первых 30 самолетов, которые приземлились в аэропорту 1 января 2006 года. Чтобы их случайные маневры до начала снижения не искажали общей тенденции движения, анализируются только 160 последних точек каждой траектории. Разница между моментами времени последовательной регистрации самолета (~ 5 с) определяется угловой скоростью вращения радара. Начало координат (0, 0, 0) совпадает с положением радара.

На рис. 1а показано трёхмерное представление для 30 анализируемых траекторий самолётов (идущих на посадку в трёх международных аэропортах, в пространстве над заливом Сан-Франциско). В численном эксперименте эти траектории разделяются на пять кластеров. В каждом из пяти кластеров, с помощью описанной выше регрессионной модели (11) выравнивания кривых в многомерном пространстве, определяется собственный тренд.

На рис. 16 вдоль вертикальной оси показано изменение скорости самолётов, происходящее со снижением высоты г, в то время как координаты (х, у) остаются неизменными. Сравнительный анализ рисунков 1а и 16 позволяет увидеть характер изменения скорости самолётов с высотой полёта. Снижение высоты происходит достаточно гладко, но оно сопровождается существенными колебаниями скорости движения самолётов.

Рисунок 2 детализирует общую картину движения самолётов (см. рис. 1), идущих на посадку. На рис. 2а, б, в показано изменение координат самолётов отдельно по каждой оси х, у, г в соответствии с индексом времени регистрации радаром. На рис. 2г представлено изменение скорости самолётов, идущих на посадку, в зависимости от этого же индекса. Количество временных точек регистрации и интервалы между ними (5 с) одинаковые для всех траекторий движения самолётов. Разница в реальном времени для самолётов, начинающих снижение, не учитывается, поэтому, на рис. 2а г по горизонтальным осям отложен индекс времени регистрации радаром. Это позволяет увидеть сходство траекторий самолётов, принадлежащих одному кластеру при изменении каждой координаты во времени. Кривые трендов, выделенные жирным, на рис. 2а г представляют собой обобщённую форму проекций траекторий кривых в кластере на соответствующие оси в зависимости от времени.

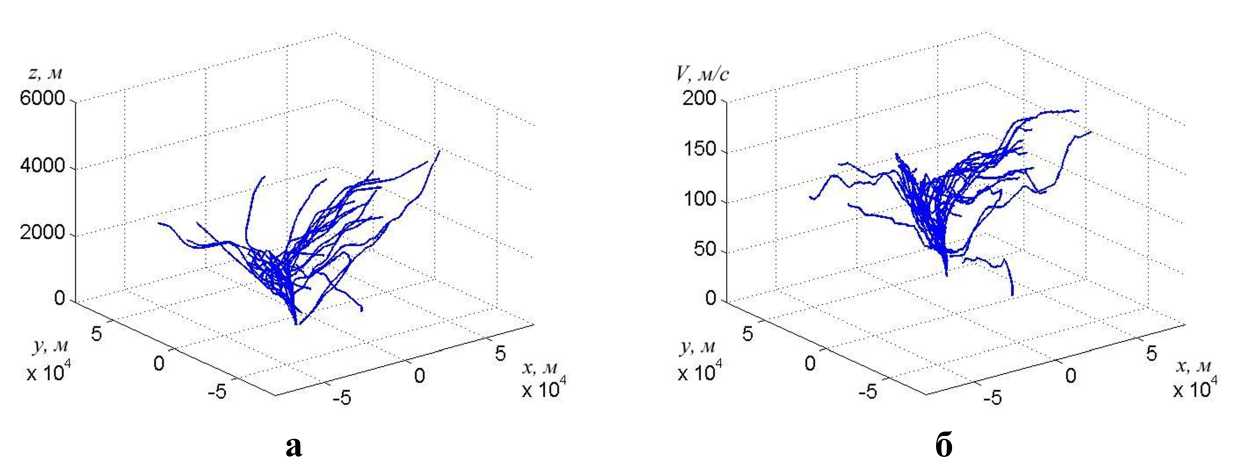
Рис. 1. Изображение для 30 траекторий самолётов, идущих на посадку: а) расположение треков в пространстве координат (х, у, г), б) расположение треков в пространстве (х, у, V), где V — скорость самолётов

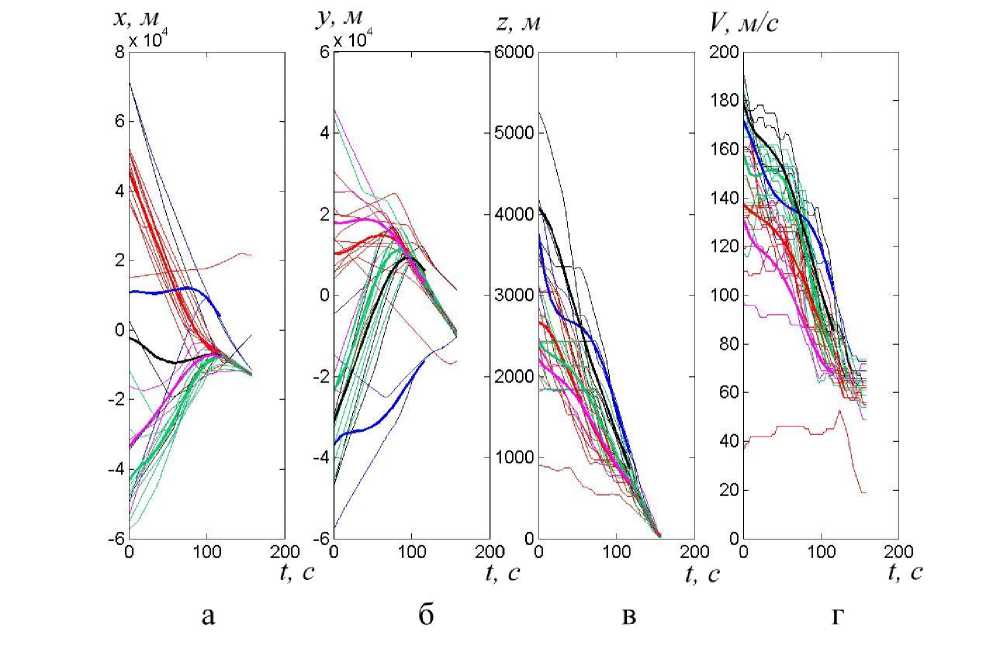
Рис. 2. а), б), в) проекции траекторий самолётов и кривых трендов (выделены жирной кривой) для пяти кластеров на координаты трёхмерного пространства в зависимости от индекса момента времени регистрации радаром, г) кластеризация самолётов, идущих на посадку, в соответствии с изменением скорости от времени

Например, на рис. 2а два кластера имеют почти линейную форму кривой тренда. На рис. 26 для этих же самых кластеров форма кривой тренда напоминает прямой угол. На рис. 2в можно заметить кривые тренда с выраженной s-образной формой кривой. Несмотря на то, что снижение самолётов происходит не синхронно в реальном времени, их сходные траектории отражают типичные маршруты посадки, когда самолёты выстраиваются в «ка- раван», ожидая своей очереди приземления на посадочную полосу. На рис. 2г показаны зависимости изменения скорости самолётов при снижении высоты. Как можно видеть из рисунков 2в и 2г, кривые трендов для изменения высоты и изменения скорости достаточно хорошо коррелируют. Рисунок 2г демонстрирует наличие случайных отклонений кривых в кластерах от кривой тренда, определяемых, по-видимому, субъективными факторами. В рассматриваемом случае такие отклонения свидетельствуют об однородности полученных кластеров, в которых невозможно выделить подгруппы кривых. В общем случае рассмотрение дополнительных характеристик при кластеризации объектов движения может способствовать более точному приписанию объекта к кластеру или поиску нового числа кластеров.

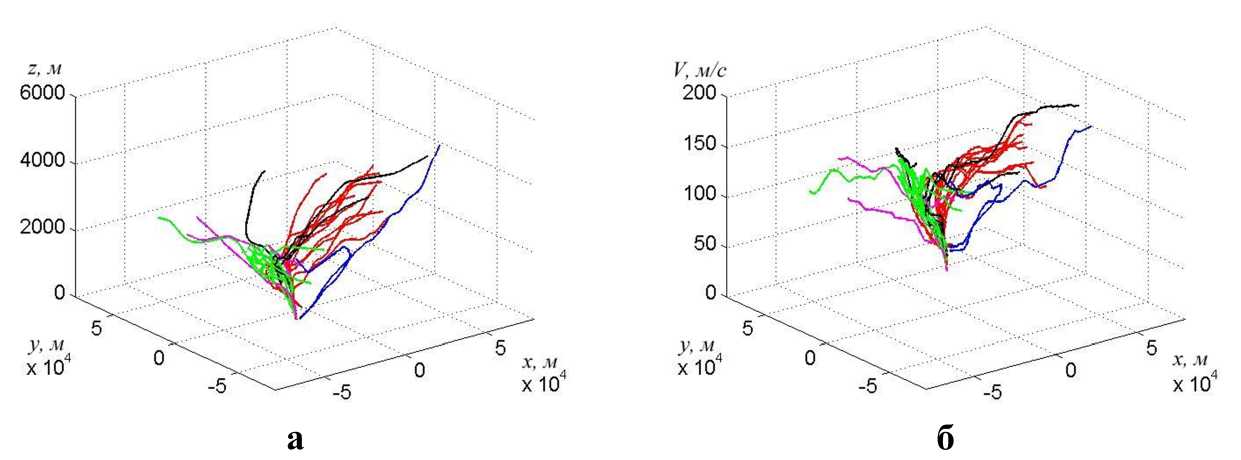
Рис. 3. Разбиение траекторий 30 самолётов, идущих на посадку, на кластеры. Каждому кластеру соответствует свой цвет: а) кластеры траекторий в пространстве координат (х,у, г), б) кластеры в пространстве (х,у, V ), где V — абсолютная скорость

На рис. 3 показан результат кластеризации траекторий самолётов, идущих на посадку, в пространстве координат и с учётом скорости, выполненной с помощью подхода, изложенного в настоящей работе. Рис. 3 является иллюстрацией эффективности метода кластеризации кривых, представленного в настоящей работе.

7.    Заключение

В настоящей работе метод одновременной кластеризации и выравнивания кривых во времени и пространстве демонстрируется на примере кластеризации траекторий самолётов, идущих на посадку в зоне крупного международного аэропорта. Эффективность кластеризации траекторий в трехмерном пространстве достигается благодаря использованию модели полиномиальной регрессии с обучением параметров посредством ЕМ-алгоритма. Дополнительное рассмотрение скоростных режимов при кластеризации объектов движения подтверждает корректность разбиения траекторий на кластеры.