Кластерный анализ на основе качества репрезентативных оценок цифровых изображений

Кластерный анализ решает задачу разбиения некоторой выборки объектов на подмножества (кластеры). При этом объекты из одного кластера должны быть подобны, а объекты разных кластеров – достаточно сильно отличаться. Алгоритмы кластеризации можно включить в более широкий класс алгоритмов обучения без учителя.

Область применения кластерного анализа включает разнообразные классы задач, такие как: интеллектуальный анализ данных, разработка классификации, сегментация изображений, сжатие данных, обнаружение нетипичных, «новых», объектов и др.

В данной работе применяется кластерный анализ для разбиения на группы выборки изображений. Кластеризация изображений, в нашем случае, является всего лишь предварительным этапом для дальнейших прикладных исследований, конечной целью которых является разработка «регулятора алгоритма распознавания» – программно-аппаратного комплекса, способного адаптировать систему распознавания образов (например, лиц) к меняющимся условиям захвата фото/видео сигнала, определяющим, в конечном счете, качество полученных изображений.

Условия работы устройства захвата сигнала могут определяться погодными факторами и степенью освещенности места, где осуществляется съемка, электромагнитными помехами в передающей среде, скоростью движения объектов захвата. Все эти и многие другие факторы вносят вклад в качество получаемых цифровых изображений. Общими критериями качества изображений могут быть яркость, контрастность, резкость, зашумленность и др.

Как известно, результаты работы алгоритмов распознавания образов, так или иначе, зависят качества входных изображений. Кроме того, оптимальные параметры этих алгоритмов могут варьироваться от изображения к изображению в зависимости от качественных характеристик исходных изображений.

Таким образом, можно выделить классы изображений (по их качественным характеристикам), для которых оптимальными будут различные наборы параметров алгоритма распознавания. Приведем пример. В качестве алгоритма распознавания рассмотрим алгоритм Кэнни ( детектор границ Кэнни) [1, 4]. В дисциплине компьютерного зрения это оператор обнаружения границ изображения. Детектор границ Кэнни до сих пор является одним из лучших детекторов. Кроме особенных частных случаев трудно найти детектор, который бы работал существенно лучше, чем детектор Кэнни.

Работа алгоритма основана на подавлении не максимумов ( Non-Maximum Suppression ), которое означает, что пикселями границ объявляются пиксели, в которых достигается локальный максимум градиента в направлении вектора градиента, а также двойной пороговой фильтрации. Параметрами алгоритма являются пороговые значения α и β , определяющие чувствительность алгоритма. Для изображений, отличных по качеству, оптимальные параметры α и β (например, с точки зрения формирования наиболее гладкого контура распознаваемого объекта) будут отличаться [1].

Таким образом, для различных изображений необходимо использовать различные наборы параметров алгоритма распознавания, а если речь идет о системе, функционирующей в режиме реального времени, то необходимо уметь динамически переключать эти наборы в зависимости от характеристик качества входного изображения, т.е. мы должны спроектировать интеллектуальный регулятор. В дальнейших работах мы планируем разработать нечеткий регулятор (НР), входные переменные которого будут определять качество исходного изображения (захватываемого видеокамерой, либо хранимого на компьютере), а выходные переменные – параметры алгоритма распознавания (например, α и β алгоритма Кэнни).

Основное преимущество НР в сравнении с другими регуляторами состоит в том, что нет необходимости знать многомерной зависимости параметров алгоритма распознавания от параметров качества изображений. Кроме того, вычисление такой зависимости потребовало бы гораздо больше вычислительных ресурсов, нежели требует работа типичного НР.

Главная компонента НР – нечеткая база знаний (БЗ).

Имеется два основных способа разработки БЗ [5]:

• 1.    Ручной. В этом случае функции принадлежности входных и выходных переменных, а также правила, описывающие поведение системы задаются непосредственно экспертом;

• 2.    Автоматизированный. БЗ формируется посредством интеллектуальной обработки обучающей выборки (так называемого «обучающего сигнала», представляющего набор пар значений типа «вход/выход») с помощью генетических алгоритмов и нейронных сетей.

Второй способ более предпочтительный, т.к. влияние субъективных знаний эксперта на конечный результат гораздо меньше (при автоматизированном способе эксперт лишь задает некоторые параметры алгоритмов обработки данных, контролирует процесс выполнения алгоритмов, дает оценку полученной БЗ). Реализации автоматизированного способа получения БЗ требует наличие обучающего сигнала.

Для нашей задачи таким сигналом будут пары: «значения параметров качества входных изображений – оптимальные параметры алгоритма распознавания». Нет смысла в качестве левых частей обучающего сигнала брать параметры качества конкретных изображений всей выборки, т.к. разброс точек обучающего сигнала будет слишком велик, а полученная зависимость сложна для аппроксимации даже с помощью НР.

Кроме того, большой размер обучающего сигнала усложняет процессы обработки данных. Поэтому предполагается выделить кластеры изображений и их центры, для каждого из которых в дальнейшем будут найдены оптимальные параметры алгоритма распознавания. Это и будет обучающим сигналом для проектирования БЗ НР системы распознавания образов.

В этой работе проводится кластерный анализ подготовленной заранее выборки изображений.

Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы:

• -    отбор выборки для кластеризации;

• -    определение множества переменных, по которым будут оцениваться объекты в выборке, то есть признакового пространства;

• -    собственно оценка значений введенных параметров для объектов выборки;

• -    выбор той или иной меры сходства между объектами выборки;

• -    выбор и применение метода кластерного анализа для создания групп сходных объектов;

• -    проверка достоверности результатов кластерного решения.

Отбор выборки для кластеризации

На начальном этапе выбраны и обработаны изображения, представляющих исходную выборку: 51 изображение различного качества, каждое размером 400*400 пикселей (см. рис. 1).

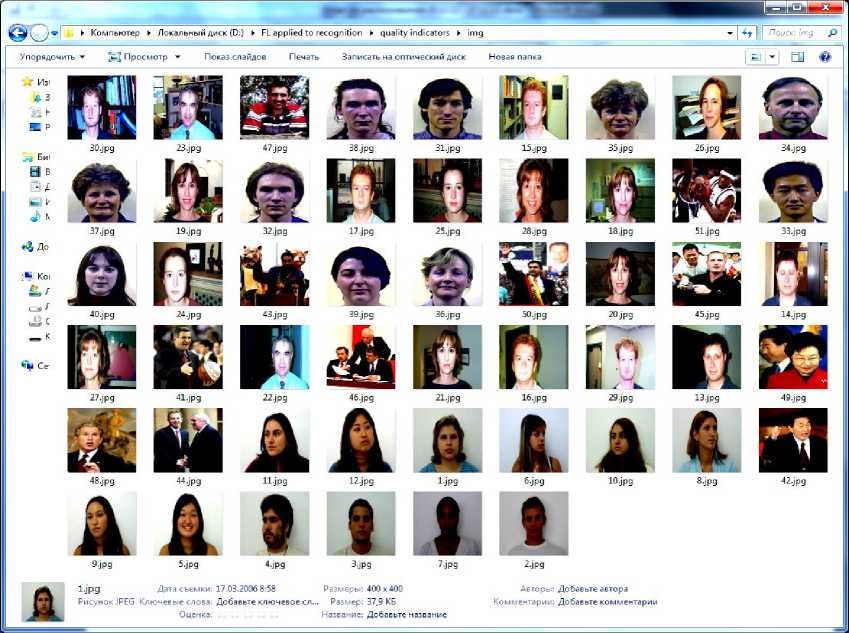
Рис. 1. Исходная выборка изображений

Определение пространства признаков

Качество аналогового изображения определяется большим количеством технических характеристик системы захвата изображения: соотношением сигнал/шум и статистическими характеристиками шума, градационными характеристиками, спектральными характеристиками, интервалами дискретизации и т.д. Эти характеристики влияют на качество оцифрованного изображения – яркость, контрастность, зашумленность и т.д. Нам необходимо найти способ вычисления этих характеристик, а также выбрать минимальное и максимальное значения шкалы их измерения, удобнее всего использовать отрезок [0, 1].

Таким образом, там, где это возможно, будет использоваться относительная яркость, относительная контрастность и т.п.

Ниже мы подробнее опишем некоторые из этих параметров качества и введем методы их оценки [4, 6].

Относительная физическая яркость

Так называемая «физическая» яркость всего изображения вычисляется по формуле:

N

Y P = 77 Z R p + ^G p + B p •

N p = 1

где R _p , G _p , B _p – значения яркости красной, зеленой и синей компонент соответственно для пикселя p .

Переход к относительным значениям осуществляется делением значения яркости всего изображения на максимально возможное значение яркости.

Относительная видимая яркость

«Видимая» яркость всего изображения вычисляется по формуле:

N

Y_P = — У 0.299 R + 0.587 G„ + 0.114 B, .

P N p = i       p         p         p

Переход к относительной видимой яркости осуществляется также как и в предыдущем случае.

Яркостная контрастность

Удобным критерием яркостной контрастности будет дисперсия яркости пикселей изображения:

N

1 ² =   f ⁽Y, - Y )².

¹ * p = 1

Более универсальный безразмерный критерий яркостной контрастности – отношение среднеквадратического отклонения к максимально возможному значению яркости:

C = 21

.

У max

Необходимо отметить, что яркостную контрастность можно вычислить как для физической, так и для видимой яркости.

Тоновая контрастность

Тоновая контрастность может быть вычислена как «средний тон»:

1N d = N f dp’ где dp = ^(Rp - R)2 + (Gp - G)2 + (Bp - B)2, a R, G, B - усредненные значения яркости красной, зеленой и синей компонент соответственно.

Тоновая насыщенность

Тоновая насыщенность – это отличие цвета от ахроматического при их одинаковой яркости. В цветовой модели RGB тоновую насыщенность пикселя можно выразить как расстояние до диагонали ахроматических цветов:

h p = V R p ² + G p ¹ + B p² - ( R p + G p + B p )²/3.

Для всего изображения оценка тоновой насыщенности может быть выражена как среднее значение тоновой насыщенности для всех пикселей:

N h = — УК • N fl p

«Блочность» – средняя абсолютная разность между блоками 8*8 пикселей

B

M ( N /8 - 1)

M N /8 - 1

£ £ | d ( i ,8 j )l, i = 1 j = 1

где d – разность интенсивностей соответствующих пикселей полутонового изображения.

Отклонение средней абсолютной разности на границе блоков от той же ве личины, вычисленной для всего изображения

1 ( ⁸

7 ( M ( N - 1)

M N - 1             A

££ d ( i , j )l - в i = 1 j = 1                     J

Кроме того, можно еще оценить среднюю длину переходных участков (участков перехода от одного цвета к другому) и среднюю высоту («крутизну») переходных участков для всего изображения. Эти два показателя позволяют оценить «резкость» исходного изображения [4, 6].

Оценка значений введенных показателей качества изображений

Мы реализовали расчет введенных показателей качества изображений для всей выборки в программной системе Matlab . Таблица расчета приведена в Приложении .

Выберем наиболее репрезентативные показатели, как показатели, у которых наибольшее расстояние между минимальным и максимальным значениями на всей выборке изображений. Так как все показатели находятся разной шкале, то необходимо нормировать всю разность на значение максимума соответствующего показателя (см., Приложение ).

Таким образом, критерий отбора наиболее репрезентативных показателей следующий:

max i - min i max _i

^ MAX , где i — номер показателя .

По этому критерию отобраны следующие 3 (из 10) показателя: относительная видимая яркость; яркостная контрастность (для физической яркости); средняя высота («крутизна») переходных участков для всего изображения («резкость»). Эти показатели отмечены в Таблице П1 Приложения зеленым цветом. Красным цветом в таблице выделен показатель с наихудшим значением критерия (1).

Следующим этапом исследования будет выбор меры сходства изображений (на множестве значений введенных показателей качества) и алгоритма кластеризации изображений.

Кластерный анализ выборки изображений

Для больших выборок и большой размерности признакового пространства сложно выполнить кластеризацию вручную, чаще используются алгоритмы кластеризации.

Для решения задачи нам из наиболее распространенных алгоритмов, подходят следующие:

• -    метод k -средних [3];

• -    кластеризация с помощью модели гауссовых смесей [2].

Широкий класс методов иерархической кластеризации мы отвергаем, т.к., в конечном счете, нас интересуют группы изображений, не связанных вертикальными связями.

Кластеризация методом k-средних

Действие алгоритма таково, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров [3].

Для работы алгоритма важна выбранная мера сходства между объектами-изображениями. Для простоты мы будем использовать меру SAD ( Sum of absolute differences ), вычисляемую по следующей формуле:

SADj^qi" - q(2) I, i=1, N где qi(1) , qi(2) – значения i-го показателя качества для первого и второго изображений.

Эта мера проста в реализации и для ее подсчета нужно немного вычислительных ресурсов.

Поскольку центры кластеров выбираются произвольно, то необходимо несколько раз выполнять алгоритм с различными координатами центров кластеров. В качестве оптимального разбиения выбирается разбиение с минимальным суммарным расстоянием точек кластера от соответствующего центра кластера. Мы будем запускать алгоритм 5 раз.

Количество выделяемых кластеров задаем произвольно. Рассмотрим работу алгоритма с различным количеством кластеров разбиения.

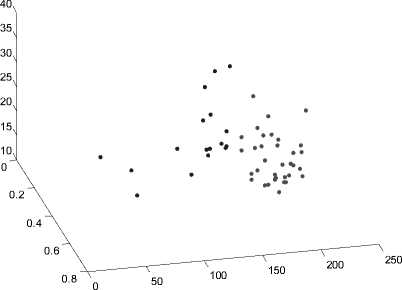
Количество выделяемых кластеров – 2. На рис. 2а представлено соответствующее разбиение.

0         0.2        0.4        0.6        0.8

Silhouette Value

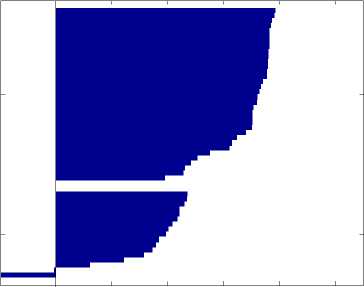
а. Разбиение выборки изображений на 2 кластера

б. График силуэтов для разбиения на 2 кластера

Рис. 2.

Для того чтобы иметь представление о том насколько хорошо выполнено разбиение, мы можем построить график силуэтов кластеров, используя выходные значения алгоритма k -средних. Этот график показывает как близко каждая точка в одном кластере близка к точка соседних кластеров. Эта мера находится в диапазоне от +1 (показывает, что точка сильно удалена от соседних кластеров) до -1 (показывает, что точка, вероятно, была приписана к данному кластеру неверно). Значение 0 показывает, что точка данного кластера неотличима от точек других кластеров.

На рис. 2б ниже изображен график силуэтов двух выделенных кластеров. Из рисунка видно, что более половины точек в первом кластере имеют большие значения силуэта (большее 0,6). Это говорит о том, что кластер 1 можно поделить еще на несколько кластеров (один из которых будет весьма большим). Второй кластер содержит только точки с малым значением силуэта и несколько точек с отрицательными значениями, что говорит о неудачном разбиении.

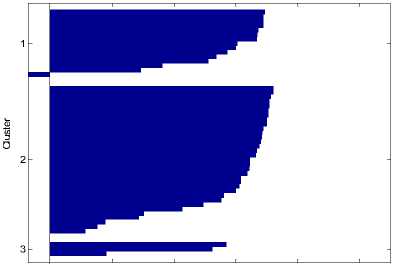
Количество выделяемых кластеров – 3. На рис. 3а представлено соответствующее разбиение. На Рис. 3б график силуэтов для этого разбиения.

0.2

0.4

0.6

0.8

Silhouette Value

• а.    Разбиение выборки изображений на 3 кластера

• б.    График силуэтов для разбиения на 3 кластера

Рис. 3.

Из рис. 3б видно, что более половины точек в первом и втором кластерах имеют большие значения силуэта (большее 0.6). Но в первом кластере есть отрицательные значения. В третьем кластере все значения силуэта менее 0.6. Теперь разделим исходную выборку на 4 кластера.

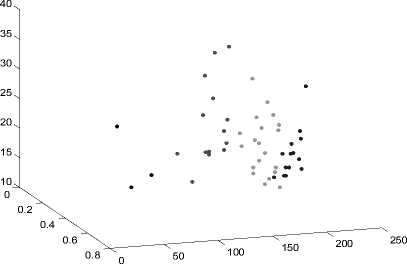
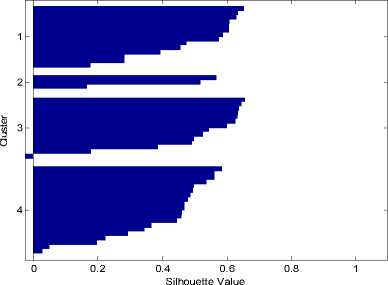
Количество выделяемых кластеров – 4. На рис. 4а представлено соответствующее разбиение. На Рис. 4б график силуэтов для этого разбиения.

• а.    Разбиение выборки изображений на 4 кластера

• б.    График силуэтов для разбиения на 4 кластера

Рис. 4.

Из рис. 4б видно, что более половины точек в первом и третьем кластерах имеют большие значения силуэта (большее 0.6). Но в третьем кластере есть отрицательные значения. Во втором и четвертом кластерах большинство значения силуэта менее 0.6. Выполним разбиение на 5 кластеров.

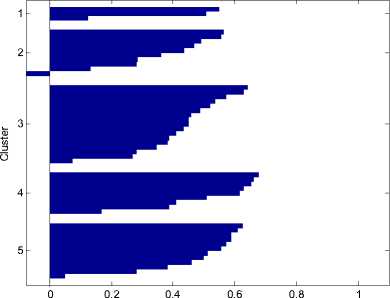
Количество выделяемых кластеров – 5. На рис. 5а представлено соответствующее разбиение. На рис. 5б график силуэтов для этого разбиения.

а. Разбиение выборки изображений на 5 кла-

стеров

Silhouette Value

б. График силуэтов для разбиения на 5 кластеров

Рис. 5.

Из рис. 5б видно, что в кластерах 3-5 только несколько точек имеют большие значения силуэта (большее 0.6). Во втором кластере есть отрицательные значения. В первом и втором кластерах большинство значения силуэта менее 0.6. Разобьем исходную выборку на 10 кластеров.

Количество выделяемых кластеров – 10. На рис. 6а представлено соответствующее разбиение. На рис. 6б график силуэтов для этого разбиения.

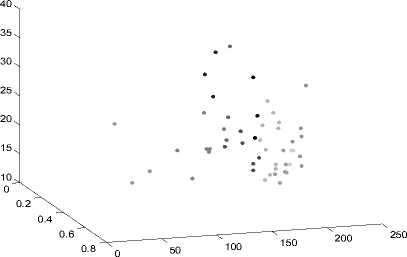
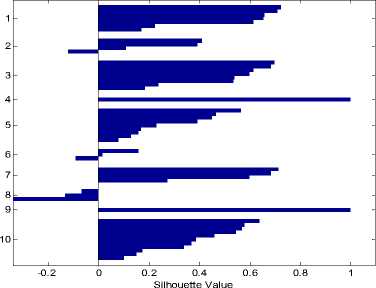
а. Разбиение выборки изображений на 10 кластеров

б. График силуэтов для разбиения на 10 кластеров

Рис. 6.

Очевидно, что при данном разбиении есть 6 - 7 удачных кластеров. Кластеры 2, 6, 8 – выделены плохо. Такое количество кластеров достаточно для получения обучающего сигнала приемлемой длины (при таком разбиении будет 7 точек в обучающем сигнале), поэтому остановимся на нем.

Кластеризация на основе модели гауссовых смесей

Данный метод реализуется на основе EM-алгоритма (Expectation-maximization algorithm) – алгоритм, используемый в математической статистике для нахождения оценок максимального правдоподобия параметров вероятностных моделей, в случае, когда модель зависит от некоторых скрытых переменных. Каждая итерация алгоритма состоит из двух шагов. На E-шаге (expectation) вычисляется ожидаемое значение функции правдоподобия, при этом скрытые переменные рассматриваются как наблюдаемые. На M-шаге (maximization) вычисляется оценка максимального правдоподобия. Таким образом, увеличивается ожидаемое правдоподобие, вычисляемое на E-шаге. Затем это значение используется для E-шага на следующей итерации. Алгоритм выполняется до сходимости [2].

EM -алгоритм используется для разделения смеси гауссовых распределений исходных значений параметров качества изображений.

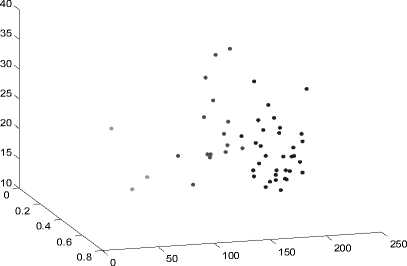
Количество выделяемых кластеров – 2. На рис. 7 представлено соответствующее разбиение.

10 0

0.8   _{0           50}          100        150         ²⁰⁰

Рис. 7. Разбиение выборки изображений на 2 кластера

Количество выделяемых кластеров – 7. На рис. 8 представлено соответствующее разбиение.

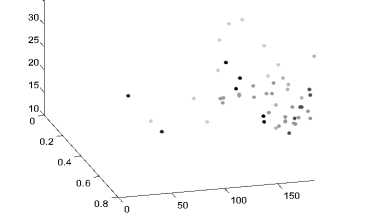
0.8

Рис. 8. Разбиение выборки изображений на 7 кластеров

Семи кластеров достаточно для последующей разработки обучающего сигнала, необходимого для проектирования БЗ НР [5], поэтому можно завершить процесс дальнейшей кластеризации. Необходимо отметить, что для модели гауссовых смесей некорректно строить график силуэтов, т.к. этот алгоритм использует функцию правдоподобия вместо функции меры сходства.

Выводы

Для разработки нечеткого регулятора, который позволит адаптировать систему распознавания образов к меняющимся условиям захвата изображений, необходимо, в первую очередь, различать изображения по качеству, а также оценивать значения показателей их качеств.

Кроме того, показатели качества изображений должны быть репрезентативными и позволять разграничивать пространство признаков изображений на характерные области.

Введенные в работе показатели качества изображений обладают вышеупомянутым свойством и их можно использовать:

• -    для предварительного отбора изображений из больших массивов в автоматическом режиме;

• -    для кластеризации выборки изображений с целью последующего получения обучающего сигнала, необходимого для проектирования базы знаний нечеткого регулятора;

• -    для расчета значений, используемых в качестве входных значений нечеткого регулятора в процессе нечеткого вывода, реализующего решение прикладных задач распознавания образов.

В данной работе мы использовали значения показателей качества изображений для кластеризации с помощью двух методов: метода k -средних и метода модели гауссовых смесей.

Метод k -средних позволяет выполнять кластеризацию для произвольного количества кластеров, а также проводить оценку качества разбиения. Для нашей выборки мы выбрали разбиение на 10 кластеров (из которых 7 выделены успешно).

При кластеризации с помощью модели гауссовых смесей мы ограничились разбиением на 7 кластеров.

Следующим шагом (после разбиения на кластеры) будет получение выходных частей обучающего сигнала для соответствующих центров выделенных кластеров (например, α и β алгоритма Кэнни).

Таким образом, мы получим два обучающих сигнала для реализации НР с 3 входами – показателями качества выходного изображениями. Данная часть обучающего сигнала является независимой от используемого алгоритма распознавания образов. Вторая (правая) часть обучающего сигнала будет зависеть от параметров выбранного алгоритма распознавания.