Кластерный анализ в геологии: метрики и меры

Недавняя статья [2] обратила внимание читателей на неисчерпанный методический ресурс кластерного анализа, активно применяемого в естественных науках. Справедливо замечено, что именно введение метрики (расстояния) превратило его в количественный анализ распределения точек в многомерном пространстве. В то же время следует подчеркнуть, что метод диалектичен: выделяя кластеры точек (что бы ни понималось под таковыми), он не только классифицирует (разделяет), но и связывает подмножества исходного точечного множества в иерархически упорядоченную структуру с нестрогим отношением порядка. В этой статье обращено внимание на то, что результат кластерного анализа существенно зависит от применяемой метрики, а расстояния между кластерами можно определять непосредственно или через меры покрывающих множеств.

Метрики

Множество называется метрическим пространством, если для любых двух его элементов i и j определено вещественное число h ij , называемое метрикой (расстоянием) и обладающее свойствами: (1, неотрицательность) h jj > 0, причём h jj = 0 тогда и только тогда, когда i = j; (2, симметричность) h jj = h ji ; (3, неравенство треугольника) для любых трёх элементов — i, j и k — выполнено h ij + h j _k > h ik [1].

На одном множестве могут быть заданы разные метрики, порождающие разные метрические пространства. Так, расстояния между точками на плоскости можно измерить привычной евклидовой (впрочем, столь же пифагоровой и декартовой, поскольку 46

основана на теореме Пифагора в декартовой ортогональной системе координат) метрикой:

h ij = [(X i - X j )² + (y_f - y j )²]^1/2 .

Непривычна, но корректна и другая метрика: h ij* = |x i - X j | + |y i - y j |.

Здесь расстояние измеряется не длиной гипотенузы, а суммой длин катетов того же треугольника. Выполнение свойств 1 и 2 очевидно. Свойство 3 легко проверяется для различных взаимных положений точек. Обе метрики обобщаются на многомерные пространства.

Ситуация получает новый акцент, если нужно найти расстояние между двумя точечными множествами, в том числе перекрывающимися по координатам точек. Нередко считается, что оно равно расстоянию между ближайшими точками множеств. Ошибочность такого решения видна из примера. Пусть совпадают две точки, принадлежащие различным множествам. Тогда расстояние между ними равно нулю. Но свойство 1 требует, чтобы в этом случае множества совпадали тождественно, т. е. всеми своими точками. Легко показать, что при указанном (неправильном) способе измерения нарушается и свойство 3. Между тем он практикуется, например, во всех компьютеризованных анализаторах петрографических структур, где под расстоянием между минеральными зёрнами понимается евклидово расстояние между точками (например, геометрическими центрами тяжести), взятыми в пределах сечений.

Для измерения расстояний между точечными множествами годится на первый взгляд странная, устроенная иерархически, рассчитываемая поэтапно минимаксная метрика Хаусдорфа:

H(I,J) = max {{max Z(i,J) | ie I}, {max Z6,I) I je J}}, где Z(i,J) = min {hy | je J}, Z6,I) = min {hji | ie I} (рис. 1). Здесь max Z(i,J) I ieI — длина отрезка [1, 1’], max Z6,I) | je J — длина отрезка [2, 2’]. Расстояние между точечными множествами I и J равно длине отрезка [2, 2’] как большей из двух. Вместо hy можно использовать hij* или другую метрику, заданную на парах точек.

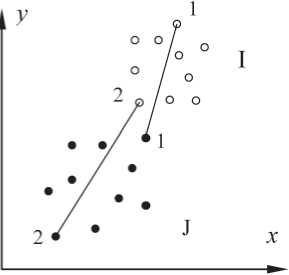
Рис. 1. Метрика Хаусдорфа

Fig. 1. The Hausdorff metric

Меры

Множество элементов называется измеримым пространством, если на его подмножествах (вообще говоря, образующих алгебру, но мы не будем углубляться в эти тонкости) определена вещественная ограниченная функция, называемая мерой и обладающая свойствами: (1, неотрицательность): p(I) > 0; (2, монотонность): если I с J, то p(I) < p(J); (3, аддитивность): если I ∩ J = ∅ , то μ(I ∪ J) = μ(I) + μ(J) [1].

Определение метрики через меры возможно и целесообразно, когда точечное множество тем или иным способом оконтуривается, т. е., по сути, покрывается фигурой с ненулевой мерой. В качестве метрик можно предложить:

p(I,J) = P(I и J) - P(I n J)

и p (I,J)* = 1 - p(I n J) / p(I и J).

В обоих случаях относительную трудность представляет проверка свойства 3 метрики. На рис. 2 для простоты точечные множества I и J оконтурены прямоугольниками. Здесь под мерами естественно понимать площади их объединения и пересечения, вычисляемые по координатам крайних точек:

p(I и J) = |max x i — min x i | x |max y i — min y i | + + |max x j — min x j | x |max y j — min y j | — — |max x j — min x i | x |max y j — min y i |,

p(I n J) = |max x j — min x i | x |max y j — min y i |.

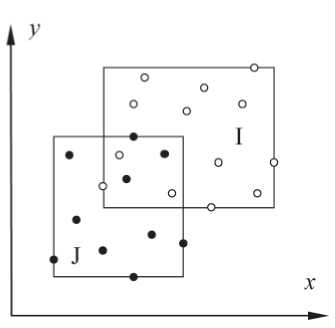
Рис. 2. Определение метрики через меру

Fig. 2. Definition of metric by measure

Заключение

Сказанное может породить вопросы: какую метрику следует применить в том или ином случае, зависит ли выбор главным образом от предметного содержания задачи или от конфигурации точечного множества. По-видимому, категорических ответов на них нет. С одной стороны, математика бесстрастна, как скальпель хирурга. С другой стороны, применяя математические методы, хорошо бы как можно лучше знать специфику изучаемого явления. Лучшим решением представляется последовательное применение в кластерном анализе нескольких метрик. Они редко приводят к полному совпадению результатов. Здесь и наступает самое интересное — попытка содержательной интерпретации различий, через которые просвечивает нечто искомое.