Кодирование изображений с использованием квадратичных кривых Безье

Одним из методов цифровой стеганографии является фрактальное кодирование изображений. Идея фрактального кодирования состоит в замене самого изображения некоторым сжимающим отображением, для которого исходное изображение (или некоторое близкое к нему) является неподвижной точкой, а для восстановления достаточно многократно применить это отображение к любому стартовому изображению. По теореме Банаха, такие итерации всегда приводят к неподвижной точке, то есть к исходному изображению [2, с. 48].

В качестве системы итерируемых функций используем систему отображений с помощью квадратичных кривых Безье:

_v JФ)=ч о - # + ^(l --01 -у? +2?>0-j) + V‘ (1)

где a0, a1, a2, b0, b1, b2 Î[0,1].

Исследование проведём в пакете прикладных математических программ SciLab. В качестве исходного изображения возьмём изображение размерности 256х256. Применим к нему базовый алгоритм фрактального кодирования [1, с. 3].

Разобьём изображение на неперекрывающиеся ранговые блоки методом квадродерева. Установим максимальную глубину квадродерева равной 6.

Покрываем изображение размерности 128х128 (после применения к нему выборки) последовательностью доменных блоков — прямоугольников. Количество строк и столбцов устанавливаем равными 16, горизонтальное и вертикальное перекрывания — половинными.

Для каждого рангового блока находим домен и соответствующее преобразование, которое наилучшим образом покрывает ранговый блок (рис. 1).

56x256

Сжимающее отображение

РмНЛЖЫК Ь:ЮХ1>

Рис. 1. Отображение доменных блоков изображения в ранговые блоки

Посредством интерполяции определяем значения пикселов в доменном блоке после отображения. Вычисляем контрастность, яркость и значение ошибки. Если значение ошибки оказывается меньше допустимой погрешности, значит, ранговый блок покрыт с допустимой погрешностью, записываем в текстовый файл номер домена, коэффициенты преобразования Безье, значения яркости и контрастности. Переходим к следующему ранговому блоку.

Для реализации итерационной схемы декодирования определим два массива изображений: domen и im. В качестве массива domen можно взять любое начальное изображение. Содержимое каждого рангового блока вычисляется применением преобразования к соответствующему доменному блоку и хранится в массиве im. Одна итерация завершается, когда обработаны все ранговые блоки. Перед началом новой итерации необходимо заменить массив domen массивом im, массив im очистить.

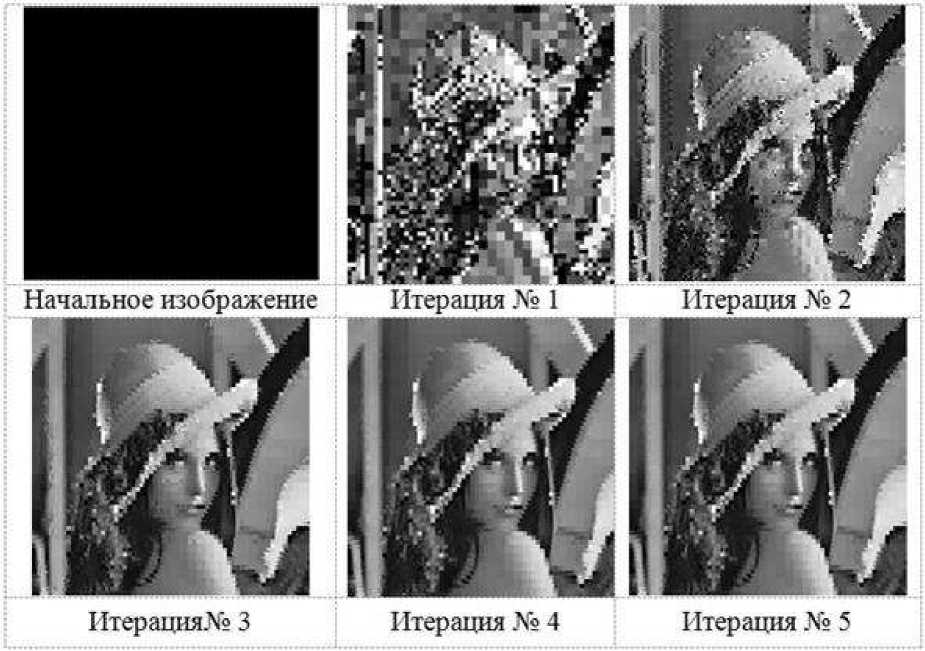
Рис. 2. Декодирование изображения с начальным однородным изображением

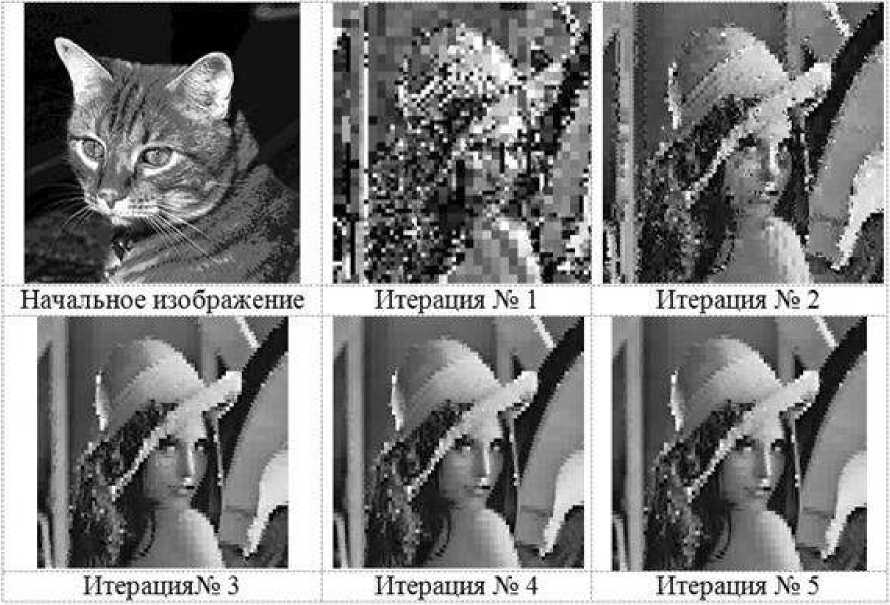
Рис. 3. Декодирование изображения с произвольным начальным изображением

Вне зависимости от начального изображения, итерации сходятся к одной и той же неподвижной точке (рис. 2, 3).

Средняя пиксельная ошибка после предварительного сжатия обоих изображений (исходного и декодированного) до размеров 64х64 равна 0,026. Стандартная количественная оценка искажений 25,4Дб.

Таким образом, было проведено фрактальное сжатие изображения с использованием среды SciLab на основе квадратичных кривых Безье, вычислены количественные оценки искажений.