Когерентная суперпозиция пучков Лагерра-Гаусса с разными длинами волн: цветные оптические вихри

Вихревые пучки или оптические вихри известны в оптике с 80-х годов, но многие фундаментальные теоретические вопросы, связанные с этими пучками, до сих пор не разрешены. И некоторые из этих нерешенных вопросов связаны с такой важной характеристикой оптических вихрей, как топологический заряд (ТЗ) [1]. Например, только недавно было показано [2], что ТЗ суперпозиции двух параллельных пучков Лагерра–Гаусса (ЛГ) с азимутальными номерами разной четности разный, в зависимости от того, кто в этой «паре» слева, а кто справа. Если пучки в суперпозиции переставить местами, то ТЗ изменится на 1. Но если про ТЗ монохроматических оптических вихрей стали появляться работы, то про расчет ТЗ «цветных» или полихроматических оптических вихрей почти нет работ. Проанализируем кратко, что известно про ТЗ полихроматических вихрей. В работе [3] освещали пучком белого света спиральную фазовую пластинку (СФП) и показали, что формируется радуга, так как разные длины волн в пучке белого света образуют после СФП световые кольца разного радиуса. В работе [4] с помощью одноосных кристаллов, освещенных полихроматическим светом, были сфор- мированы оптические вихри первого и второго порядков. Их ТЗ был экспериментально измерен с помощью цилиндрической линзы. С помощью фильтров, выделяя из белого вихря разные спектральные составляющие, было показано, что ТЗ каждой цветной составляющей в пучке одинаковый и равен 1 или 2 [4]. В [5] освещали белым светом многосекторную спиральную отражающую метаповерхность, сформированную на поверхности пленки золота и состоящую их бинарных субволновых решеток, поворачивающих вектор поляризации падающего света. Было экспериментально показано, что такая поверхность формирует при отражении вихри первого порядка во всем видимом диапазоне с почти одинаковой эффективностью (около 60 %). В [6] цветные оптические вихри формировались с помощью решетки Брегга с вилочкой, сформированной в холестерическом жидком кристалле. Такая решетка Брегга работает как «толстая» голограмма, которая обладает существенной угловой селективностью. Меняя угол падения белого света на поверхность жидкого кристалла, на выходе получали цветные (красные и синие) оптические вихри первого и второго порядков. В [7] белым светом от светодиода освещали отражающий модулятор, на котором сформирована спиральная картина фазы, наложенная на пилообразную дифракционную решетку. Решетка отражает свет разных длин волн под разными углами. Экспериментально были получены цветные (красный, зеленый и синий) оптические вихри с топологическим зарядом 3. Белый оптический вихрь в [7] получали, помещая в оптическую схему призму, которая компенсировала дисперсию решетки модулятора.

Работ по «цветным» оптическим вихрям (ЦОВ) не много, тем более мало работ (или почти нет) по расчету ТЗ суперпозиции ЦОВ. В данной работе на примере осевой когерентной суперпозиции однокольцевых (радиальный индекс равен нулю) пучков ЛГ с одинаковым радиусом перетяжки, но разными весовыми коэффициентами, ТЗ и длинами волн, мы покажем теоретически и численно, что в топологической конкуренции выигрывает более «красный» пучок ЛГ и ТЗ всей суперпозиции равен ТЗ того пучка ЛГ, у которого больше длина волны.

Заметим, что в отличие от орбитального углового момента ТЗ является дискретной характеристикой вихревых пучков. Поэтому для изменения ТЗ требуются более сильные искажения светового поля и, следовательно, ТЗ – более устойчивая величина [1], которую можно использовать для идентификации сигналов в оптической передаче информации. Результаты данной работы, таким образом, призваны установить теоретические значения ТЗ для задач передачи информации в многоцветных световых пучках.

1. Топологический заряд суперпозиции двух цветных оптических вихрей

Под цветными оптическими вихрями в работе понимается осевая когерентная суперпозиция однокольцевых пучков ЛГ с одинаковыми перетяжками, но разными топологическими зарядами (ТЗ) и разными длинами волн. Комплексная амплитуда таких цветных оптических вихрей описывается выражением:

N

E ( r , ф , z , t ) = £ c s q sn s -1

s =1

( z )

w

x exp

r ² w ² q s ( z )

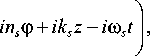
где ( r , φ, z ) – цилиндрические координаты, t – время, w – радиус перетяжки Гауссова пучка, с s – весовые постоянные, n s – топологические заряды каждого пучка в суперпозиции,

z        ksW2

qs (z) = 1 + i—, Zs = ——, ks =— ,(2)

zs 2

z s – длина Рэлея, k s – волновое число света, λ s – длина волны монохроматического света, а ω s – его частота ( k s = ω s / c , c – скорость света в вакууме). На практике

суперпозиция (1) сформируется, если в перетяжке осевой суперпозиции Гауссовых пучков с определенными длинами волн разместить спиральную фазовую пластинку (СФП) порядка n с глубиной рельефа, рассчитанного на длину волны λ 0 . Длины волн λ s у Гауссовых пучков должны быть такими, чтобы порядок СФП оставался целым числом n s : X _sn_s = X 0 n , s = 1, 2, 3,…, N . Строго говоря, после СФП сформируется в этом случае не пучок ЛГ, а Гауссов оптический вихрь [8]. Но в ряде работ показано, что Гауссов вихрь в дальней зоне почти совпадает с пучком ЛГ [9, 10].

Далее для простоты выкладок рассмотрим только два слагаемых в (1). Топологический заряд будем рассчитывать по формуле Берри [11]

1 г T 2T ^{d E} ( r , ф ^, z ) / ^дф TC = —limIm d ф ——-- ——.

2 n r ^ ^ю *        E ( r , ф , z )

Из (3) кажется, что правая часть зависит от расстояния z . Однако ниже будет показано, что топологический заряд от z не зависит.

Подставим (1) при N = 2 в (3), получим:

TC =

x exp

n

r ²

----—+ in ф+ ik 1 z - i tot + w ² q ( z )

m imc2 I V2r I exp qm+1 ( z)( w J

r ²                          ,

----—+тф+ikz-itot rx wq2(z)         2 J

I

I Ci I V2r I rr, x< —   exp--—+inф+ikz - i to, t

|qn+1 (z)( w J P[ w2qi(z)

C 2    I V2 r ) m

+------ exp q ™ ⁺¹ ( z ) ( w J

r ²

w ² q 2 ( z )

+

+ 1т ф+ ik₂ z - i ® 2 1

-1

> d ф.

Предполагая, что у обоих пучков ненулевая амплитуда: c 1 ≠ 0, c 2 ≠ 0, и делая замену переменной r = w ρ / 2^1/2, это выражение можно переписать в следующем виде:

1            2 ^Л

TC =—lim Re | d ф{ m exp( imф) + n exp( шф) x xP(z)pn-mexp[-Q(z)p2 + i(k1 -k2)z-i(«1 -©2)tJ}x (4) x {exp (imф) + exp (in ф) x xP(z)pn-mexp[-Q(z)p2 + i(k1 -k2)z-i(©1 -©2)tJ} ,

где

^P ( z ) =

C 1 qTM , C 2 q n ^{+ 1} ( z )

Q ( z ) = 2

q 1 ( ^z ) q 2 ( ^z )

Из (4) следует, что если | q 1 ( z )| < | q 2 ( z )|, то в показателях экспонент с ρ² стоит число с отрицательной вещественной частью, и при стремлении ρ к бесконечности вторые слагаемые под интегралом в числителе и знаменателе стремятся к нулю, независимо от отношения номеров n и m и независимо от весовых множителей c 1 и c 2 . Оставшиеся первые слагаемые после сокращения подобных сомножителей дают результат TC = m . И наоборот, если | q 1 ( z )| > | q 2 ( z )|, то в показателях экспонент с ρ² стоит число с положительной вещественной частью, и при стремлении r к бесконечности вторые слагаемые тоже стремятся к бесконечности. И первыми слагаемыми можно пренебречь. Тогда, сокращая подобные сомножители в числителе и знаменателе под интегралом, получим, что TC = n. Из (2) следует, что | q 1 ( z )| < | q 2 ( z )|, если X 1 < X 2 (и TC = m ), и | q i ( z )| > | q 2 ( z )|, если X 1 > X 2 (и TC = n ). Таким образом, можно утверждать, что ТЗ суперпозиции из двух цветных оптических вихрей равен ТЗ того пучка, у которого длина волны больше («красные» выигрывают у «синих»). Если учитывать соотношение X s n s = Х 0 n , s = 1,2,..., N , то у пучка с большей длиной волны топологический заряд будет меньше.

Заметим, что в случае большего числа пучков ( N > 2) доказательство более громоздкое, но аналогичное – одна из экспонент преобладает над другими и ТЗ суперпозиции равен ТЗ пучка с большей длиной волны.

Также заметим, что если вместо однокольцевых пучков ЛГ в суперпозиции (1) взять пучки ЛГ с ненулевыми радиальными индексами p s :

очень трудно, так как нужно, чтобы в перетяжках каждого из цветных Гауссовых пучков были расположены разные СФП, у которых максимальная глубина рельефа h s согласуется с длиной волны λ s падающего света: 2 п h_s ( n 0 -1) = n X _s , где n 0 - показатель преломления материала СФП (считаем, что дисперсии показателя преломления нет).

2. Топологический заряд белого оптического вихря

Рассмотрим практически важный случай, когда в перетяжку белого оптического вихря (непрерывный спектр из видимого диапазона) помещается одна СФП порядка n , рельеф которой согласован с длиной волны λ 0 . Тогда комплексная амплитуда суперпозиции в зоне дифракции Френеля будет иметь вид:

E ( p , 9 , z , t ) = — JX^{- 1} f ( X ) d X j rdr J d фx z                      0

1,2л z x exp< z--

I X

. 2п ct

1-----------

X

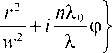
x

x exp

,

где f (λ) – огибающая спектра источника белого света (например, светодиода). Так как ТЗ каждого монохроматического (одноцветного) вихря ц = n X ₀/ X будет, вообще говоря, дробный, то интегрировать по φ в (6) нельзя, и мы разложим экспоненту в ряд по оптическим вихрям с целым ТЗ:

N

E ( r , ф , z , t ) = У cq n ^{- 1}

s =1

n s

2 r 1

w

n s L p s

2 r ²

w ² q s ⁽ z )|²

[ . nXo    ]

exp l z ----ф I =

V X J

_ e* ^{п n X o/ X}X sin( n n X _o / X )

п

j        ,>un ф

У "T ern =-j n X o - m X

x exp

r ²

——— + m_s ф - 2 z^ s arg q s ( z ) + k s z - 1 ® s t w ² q s ( z )

Подставив (7) в (6), получим:

где Lⁿ_p (.) – присоединённый многочлен Лагерра, то аналогичный вывод приведёт к точно такому же ТЗ, поскольку он определяется доминирующей экспонентой (Гауссовой огибающей пучка), а не степенями при радиальной координате.

Пусть в (1) ТЗ всех пучков в суперпозиции равны n , тогда вместо (1) запишем:

E ( r , ф , z )

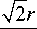
w

e^{n ф} x

N x^ c.q.n-1( z) exp s=1

r ² w ² q s ( z )

+ zk_sz

И так как производная от (5) будет равна d E ( r , ф , z )/ дф = znE ( r , ф , z ), то из (3) сразу следует, что ТЗ суперпозиции (5) с любой комбинацией цветов равен ТЗ каждого пучка: TC = n . Это простой результат, но сформировать на практике суперпозицию (5)

-j

E ( p , 9 , z , t ) =---- У ( - i ) e *m ⁹x z X o m t-„^V

^j e^{i (n/X)( n X o +p2/ z + 2 z - 2} ct ) sin ( п n X _o/ X ) f ( X ) d _X

0            nXo - mX

j xj exp

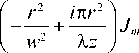
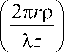
rdr ,

где J m ( x ) – функция Бесселя первого рода m -го порядка. Интеграл по переменной r в (8) можно вычислить, используя справочный интеграл [12]:

j , Г r2 znr2) . ( 2пrp) rdr expl--- ■ — I Jm l —-- I =

o V w2   Xz J V X z J

_ n^3/2 p w ³ ( X z )^1/2(sgn m )l m l

=                 :    7x3/2      ^x

4 (X z -z п w2)

x e ^Ч[ I (| m |-1)/2 ( ^ ) - I (I m |+1)/2 ( ^ ) ] ,

где t =          " ) 2    ..

2Xz (Xz - i п w2)

Подставляя (9) в (8), окончательно получим:

/ „ х   - i п ^3,2 р w ³

En (p,9,z,t) =------------x

n ⁽          ) 2 z ^1/2 X ₀

да x £ (-i)m(sgnm)meim9Dm,n (p,z,t), m =-да

,      , да e ^[I(|m|-1)/2© I(|m+1)/2©J где Dm,n (p, z, t) = J-----------------372-------->

о       (X z - i п w2)

e i (ⁿA⁾⁽ n a ² z +2 z -2 ct ^m sin( n _n х _о / x) f ( X ) x------------------------------------------- d X.

nX0 - mX

Интеграл (11), скорее всего, нельзя свести к справочному интегралу и поэтому нельзя вычислить в явном виде, кроме тривиального случая монохроматического света, когда f ( X ) = 5 ( X - X ₀). В этом случае выражение (10) совпадает с уравнением (45) в работе [13]. Но и без вычисления (11) можно сделать некоторые выводы из полученных выражений (10) и (11). А именно, если в знаменателе функции под интегралом будет ноль, тогда из всего ряда в (10) останутся только слагаемые с номерами m , которые обеспечивают этот ноль в знаменателе:

m = —°, Xe[X0-AX, X0+AX], (12) X где 2AX - ширина спектра цветного Гауссова пучка. Например, если n = 10, Хо = 532 нм, AX = 100 нм, то в сумме (10) останутся всего 4 слагаемых с номерами m = 9, 10, 11, 12. Далее можно пользоваться выражением (1), которое показывает, что в суперпозиции эффективно имеются всего 4 пучка и ТЗ всей суперпозиции будет равен максимальному ТЗ, то есть TC = 12. Если увеличить порядок СФП в 2 раза, пусть n = 20, то в рамках того же примера в сумме (10) останутся уже 8 цветных оптических вихрей с номерами m от 17 до 24. То есть в суперпозиции (10) эффективно будут распространяться 8 оптических вихрей (1) и ТЗ такой суперпозиции будет равен TC = 24. И наоборот, если уменьшить порядок СФП, например, взять n = 3, как в работе [7], для пучка с любой длиной волны из диапазона [432 нм, 632 нм] в сумме (10) только одно слагаемое будет давать вклад при m = 3. Это объясняет результат эксперимента в [7], после прохождения одной СФП порядка n = 3 все цветные вихри (белый, синий, красный и зеленый) имели ТЗ, равный m = 3.

• 3.    Моделирование

  • 3.1.    Моделирование двухцветных вихрей

Рассмотрим когерентную суперпозицию двух пучков ЛГ разного цвета. Согласно (1), такое световое поле не является стационарным и зависит от вре- мени. Допустим, что в некоторой точке пространства комплексная амплитуда первого пучка равна A, а комплексная амплитуда второго пучка равна B. Тогда поле в этой точке зависит от времени следующим образом: E = A exp(– iω1t) + B exp(– iω2t), где ω1 и ω2 – частоты обоих пучков. В простом случае, когда A = B, это поле может быть представлено как E =2A cos[(ω1 – ω2)t /2] exp[– i (ω1 + ω2) t /2]. Этот простой пример показывает, что если частоты ω1 и ω2 не близки друг к другу, то интенсивность поля меняется от нуля до максимума с частотой, гораздо большей, чем способен воспринимать человеческий глаз. Поэтому эта точка пространства воспринимается как точка с постоянной интенсивностью | A|2 и с усреднённой частотой (ω1 + ω2) /2. Соответственно, если пучки имеют, например, синий и красный цвет, то при равенстве амплитуд в некоторой точке она выглядит как фиолетовая и при визуализации двух интерферирующих пучков может быть отображена как (255, 0, 255) (в формате RGB). Что касается фазы, то в отличие от монохроматических пучков она не определена, так как в каждой точке пространства колебания не гармонические. Поэтому визуализировать можно только мгновенную фазу, в некоторый конкретный момент времени.

На рис. 1 показана суперпозиция двух пучков ЛГ разного цвета. Распределения интенсивности (рис. 1 а , г , ж ) показаны усреднёнными по времени, а распределения фазы (рис. 1 б , в , д , е , з , и ) – мгновенные (в два разных момента времени). Для расчётов были выбраны следующие параметры: длины волны λ 1 =400 нм, λ 2 =700 нм, радиус перетяжки Гауссова пучка w = 500 мкм, топологические заряды пучков соответственно n 1 =4 и n 2 =3, радиальные индексы p 1 = p 2 =0 (однокольцевые пучки), весовые коэффициенты суперпозиции c 1 = [ p 1 ! /( n 1 + p 1 )!]^1/2 ≈ 0,2 и c 2 = [ p 2 ! /( n 2 + p 2 )!]^1/2≈ 0,4 (при таких коэффициентах энергии обоих пучков равны), расстояние вдоль оптической оси z =0,2 м (рис. 1 а – в ), z = 1 м (рис. 1 г – е ), z =2 м (рис. 1 ж – и ), время регистрации фазы t 1 =60 с (рис. 1 б , д , з ) и t 2 = 61 с (рис. 1 в , е , и ).

Так как ТЗ синего пучка больше, чем красного, то на небольшом расстоянии радиус синего кольца больше радиуса красного (рис. 1 а ). Однако красный пучок расходится сильнее, чем синий. Поэтому на расстоянии примерно 1 м радиусы колец выравниваются (одно фиолетовое кольцо на рис. 1 г ) и далее, на расстоянии около 2 м, красное кольцо становится внешним, а синее – внутренним (рис. 1 ж ).

Согласно теории, общий топологический заряд всей суперпозиции не зависит от того, какого цвета кольцо является внешним, и определяется только топологическим зарядом пучка с большей длиной волны. Тогда для пучка с рис. 1 он должен быть равен трём ( TC =3). Расчёт топологического заряда по мгновенным распределениям фазы на рис. 1 это подтверждает: при расчёте по формуле М.В. Берри (3) вдоль окружности радиуса

R 1 =7,5 мм были получены значения 2,986 (рис. 1 б ), 2,982 (рис. 1 в ), 2,874 (рис. 1 д , е ), 2,907 (рис. 1 з , и ).

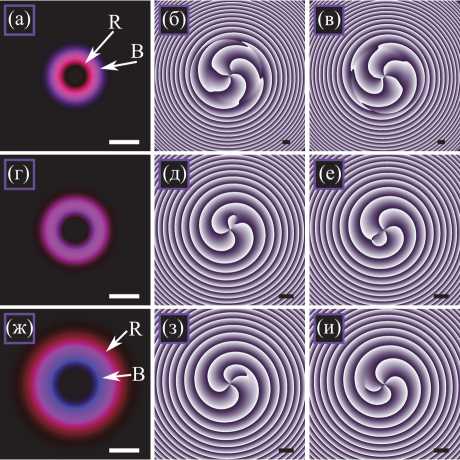
Рис. 1. Усреднённые распределения интенсивности (а, г, ж) и мгновенные распределения фазы (б, в, д, е, з, и) суперпозиции двух однокольцевых пучков ЛГ разного цвета (λ 1 = 400 нм, λ 2 = 700 нм) на расстоянии z = 0,2 м (а – в), z = 1 м (г – е), z = 2 м (ж – и) в моменты времени t 1 = 60 с (б, д, з) и t 2 = 61 с (в, е, и). Другие параметры расчёта: радиус перетяжки Гауссова пучка w = 500 мкм, ТЗ n 1 = 4 и n 2 = 3, радиальные индексы p 1 = p 2 = 0, весовые коэффициенты суперпозиции c 1 ≈ 0,2 и c 2 ≈ 0,4 (для выравнивания энергии пучков). Масштабная метка на каждом рисунке показывает 1 мм. Тёмный и светлый цвет на распределениях фазы означают соответственно 0 и 2π.

Символы ‘R’ и ‘B’ (а,ж) показывают области доминирования соответственно красного и синего пучка

В начальной плоскости и в начальный момент времени оптические вихри в сечении пучка распределены так. В центре пучка на оптической оси находится оптический вихрь с меньшим ТЗ 3, а на некотором радиусе от оси находится вихрь с ТЗ +1 и на большем радиусе вихрь с ТЗ –1. При эволюции суперпозиции во времени и пространстве на оптической оси по-прежнему остается вихрь с ТЗ +3, а оптический «диполь» с ТЗ на краях +1 и –1 приближается к оптической оси. То есть ТЗ суперпозиции равен 3. Эту эволюцию можно видеть на распределениях мгновенной фазы на рис. 1. По-другому вели бы себя вихри, если бы, наоборот, у большей длины волны был ТЗ 4, а у меньшей 3. Тогда при эволюции суперпозиции вихрь с ТЗ –1 «почти мгновенно» ушел бы на бесконечность, а вблизи оси сформировался бы вихрь с ТЗ 4 и у всей суперпозиции ТЗ был бы равен 4.

Аналогично и для многокольцевых пучков ЛГ. На рис. 2 показана суперпозиция двух пучков ЛГ разного цвета с теми же параметрами, что и на рис. 1, но радиальные индексы пучков равны p1 = p2 =2 (у каждого пучка три кольца). Соответственно, для выравнивания энергии весовые коэффициенты суперпозиции выбраны равными c1 = [p1! /(n1 + p1)!]1/2 ≈ 0,053 и c2= [p2! /(n2+ p2)!]1/2 ≈ 0,129.

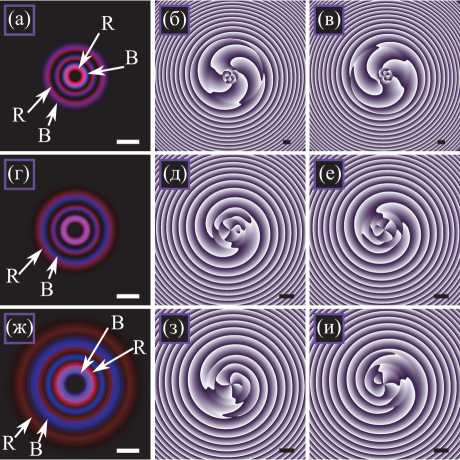
Рис. 2. Усреднённые распределения интенсивности (а, г, ж) и мгновенные распределения фазы (б, в, д, е, з, и) суперпозиции двух трёхкольцевых пучков ЛГ разного цвета (λ 1 = 400 нм, λ 2 = 700 нм) на расстоянии z = 0,2 м (а – в), z = 1 м (г – е), z = 2 м (ж – и) в моменты времени t 1 = 60 с (б, д, з) и t 2 = 61 с (в, е, и). Другие параметры расчёта: радиус перетяжки Гауссова пучка w = 500 мкм, ТЗ n 1 = 4 и n 2 = 3, радиальные индексы p 1 = p 2 = 2, весовые коэффициенты суперпозиции c 1 ≈ 0,053 и c 2 ≈ 0,129 (для выравнивания энергии пучков). Масштабная метка на каждом рисунке показывает 1 мм. Тёмный и светлый цвет на распределениях фазы означают соответственно 0 и 2π. Символы ‘R’ и ‘B’ (а, г, ж) показывают области доминирования соответственно красного и синего пучка

Так как ТЗ синего пучка больше, чем красного, то на небольшом расстоянии радиусы всех трёх колец у синего пучка больше радиусов соответствующих трёх колец красного пучка (рис. 2 а ). Так как красный пучок расходится сильнее, чем синий, на расстоянии примерно 1 м радиусы внутренних (самых ярких) колец выравниваются и получается одно фиолетовое кольцо (рис. 2 г ), в то время как у двух внешних красных колец радиусы уже больше, чем у синих. Далее на расстоянии около 2 м все три красных кольца становятся внешними по отношению к трём синим кольцам (рис. 2 ж ).

Согласно теории, наличие нескольких колец и их радиусы не влияют на общий топологический заряд всей суперпозиции и, как и на рис. 1, он должен быть равен трём ( TC =3). Расчёт топологического заряда по формуле М.В. Берри по мгновенным распределениям фазы на рис. 2 это подтверждает. Численно получены значения 2,987 (рис. 2 б ), 2,982 (рис. 2 в ), 2,874 (рис. 2 д , е ), 2,907 (рис. 2 з , и ).

• 3.2.    Моделирование трёхцветного вихря

Возникает вопрос, а могут ли аналогично три пучка Лагерра–Гаусса трёх разных цветов быть пространственно разделены в начальной плоскости, за- тем сложиться в одно кольцо и сформировать оптический вихрь, который выглядит белым или серым (суперпозиция красного, зелёного и синего пучков), и затем снова разделиться? На расстоянии z от начальной плоскости радиус кольца максимальной интенсивности каждого из этих трёх вихрей равен

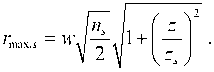
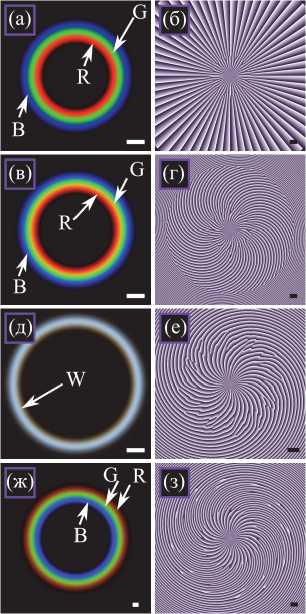
Если эти радиусы примерно равны для всех трёх вихрей, то должно выполняться условие:

n 1

1 +

z

* n 3

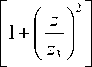
Отсюда видно, что три вихря не могут сложиться на малых расстояниях ( z <<  z 1 , z 2 , z 3 ), так как в этом случае их топологические заряды должны быть примерно одинаковы и потому в начальной плоскости эти три кольца не могут быть пространственно разделены. Допустим теперь, что пучки складываются в зоне дифракции Френеля и пройденное расстояние равно, например, среднему расстоянию Рэлея трёх пучков. Положим для определённости λ 1 < λ 2 < λ 3 . Тогда с учётом одинакового радиуса перетяжки у всех трёх пучков, положив в (14) z = z 2 , получим соотношение для топологических зарядов:

n 2 1

n 1 * 2

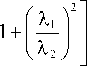
n 2 1

n T * 2

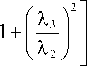
Допустим, что длины волн интерферирующих пучков равны λ 1 = 400 нм, λ 2 = 550 нм, λ 3 = 700 нм. Тогда n 2 / n 1 ≈ 0,76 ≈ 3 / 4 и n 2 / n 3 ≈ 1,31 ≈ 4 /3. Например, можно выбрать n 1 = 16, n 2 = 12, n 3 = 9. Однако эти топологические заряды невелики, и согласно (13) радиусы колец максимальной интенсивности в начальной плоскости близки друг к другу: r max,1 ≈ 2,83 w , r max,2 ≈ 2,45 w , r max,3 ≈ 2,12 w . Учитывая, что толщина каждого кольца сопоставима с радиусом перетяжки w , эти три кольца в начальной плоскости не разделены. Поэтому для расчёта увеличим порядок каждого пучка в четыре раза: n 1 = 64, n 2 = 48, n 3 = 36.

На рис. 3 показаны усреднённые распределения интенсивности и мгновенные распределения фазы суперпозиции трёх однокольцевых пучков ЛГ разного цвета (λ 1 =400 нм, λ 2 =550 нм, λ 3 =700 нм) на расстояниях z =0 м, z = z 3 /2 ≈ 0,56 м, z = z 2 ≈ 1,43 м, и z =2 z 3 ≈ 3,93 м в момент времени t =60 с. Другие параметры расчёта: радиус перетяжки Гауссова пучка w =500 мкм, топологические заряды n 1 =64, n 2 =48 и n 3 =36, радиальные индексы p 1 = p 2 = p 3 =0, весовые коэффициенты суперпозиции c s = 1 / ( n s !)^1/2, s = 1,2,3 (для выравнивания энергии пучков).

Рис. 3. Усреднённые распределения интенсивности (а, в, д, ж) и мгновенные распределения фазы (б, г, е, з) суперпозиции трёх однокольцевых пучков ЛГ разного цвета (λ 1 = 400 нм, λ 2 = 550 нм, λ 3 = 700 нм) на расстоянии z = 0 м (а, б), z = z 3 / 2 ≈ 0,56 м (в, г), z = z 2 ≈ 1,43 м (д, е), и z = 2z 3 ≈ 3,93 м (ж, з) в момент времени t = 60 с. Другие параметры расчёта: радиус перетяжки Гауссова пучка w = 500 мкм, топологические заряды n 1 = 64, n 2 = 48 и n 3 = 36, радиальные индексы p 1 = p 2 = p 3 = 0, весовые коэффициенты суперпозиции c s = 1 / (n s !)^1/2, s = 1, 2, 3 (для выравнивания энергии пучков). Масштабная метка на каждом рисунке показывает 1 мм. Тёмный и светлый цвет на распределениях фазы означает соответственно 0 и 2π. Символы ‘R’, ‘G’ и ‘B’ (а, в, ж) показывают области доминирования соответственно красного, зелёного и синего пучка. Символ ‘W’ (д) показывает белое (светлосерое) кольцо, образованное сложением трёх пучков

Так как при заданных параметрах топологический заряд пучков убывает с длиной волны, в начальной плоскости и на небольшом расстоянии от неё красное кольцо находится внутри зелёного, а зелёное – внутри синего (рис. 3 а , в ). Также видно, что из-за расширения пучков при распространении границы между пучками (кольца низкой интенсивности) на рис. 3 в становятся менее отчётливыми, чем на рис. 3 а . Так как расходимость пучков увеличивается с длиной волны, красный пучок расходится сильнее всех, а синий – слабее. За счёт подбора топологических зарядов с помощью условия (15) на расстоянии Рэлея зелёного пучка ( z = z 2 ≈ 1,43 м) во всех трёх пучках формируется кольцо одинакового радиуса, и потому дифракционная картина выглядит как одно белое (светло-серое) кольцо (рис. 3 д ). Далее за счёт разной расходимости кольца

снова разделяются, но уже синее кольцо становится внутренним, а красное – внешним (рис. 3 ж ).

Согласно теории общий топологический заряд всей суперпозиции равен топологическому заряду пучка с большей длиной волны. Для выбранных параметров он должен быть равен TC =36. При численном расчёте по мгновенным распределениям фазы с рис. 3 по формуле М.В. Берри (3) вдоль окружности радиуса R 1 ≈ 9,3 мм были получены значения 63,944 (рис. 1 б ), 35,847 (рис. 1 г ), 35,775 (рис. 1 е ), 35,934 (рис. 1 з ), то есть расчёт подтверждает теоретическое значение TC =36 во всех поперечных плоскостях, кроме начальной. В начальной плоскости получено значение TC =64, потому что периферийные вихри –1-го порядка находятся за пределами расчётной области, но уже при z = z 3 /2 (половина самого меньшего из трёх расстояний Рэлея – для красного пучка) на распределении фазы (рис. 3 г ) присутствуют 28 вихрей –1-го порядка, поэтому итоговый топологический заряд оказался равен 36 (64–28).

• 3.3.    Моделирование трёхцветного вихря

с разными сочетаниями цветов световых колец

Во всех рассмотренных случаях (рис. 1 –3) топологический заряд пучков убывал с длиной волны. Поэтому может показаться, что топологический заряд всей суперпозиции равен не топологическому заряду пучка с наибольшей длиной волны, а наименьшему из топологических зарядов. Чтобы подтвердить теоретический вывод, что топологический заряд определяется исключительно длиной волны, рассмотрим всевозможные сочетания трёх цветов и трёх топологических зарядов. Таких сочетаний шесть.

На рис. 4 показаны усреднённые распределения интенсивности и мгновенные распределения фазы этих шести различных суперпозиций трёх однокольцевых пучков ЛГ разного цвета (λ 1 =400 нм, λ 2 =550 нм, λ 3 =700 нм) на расстоянии z = z 2 /2 ≈ 0,71 м в момент времени t =60 с. Другие параметры расчёта: радиус перетяжки Гауссова пучка w = 500 мкм, топологические заряды n 1 = 1, n 2 =2 и n 3 =4 (рис. 4 а , б ), n 1 = 1, n 2 =4 и n 3 =2 (рис. 4 в , г ), n 1 =2, n 2 = 1 и n 3 =4 (рис. 4 д , е ), n 1 =2, n 2 =4 и n 3 = 1 (рис. 4 ж , з ), n 1 =4, n 2 = 1 и n 3 =2 (рис. 4 и , к ), n 1 =4, n 2 =2 и n 3 = 1 (рис. 4 л , м ), радиальные индексы p 1 = p 2 = p 3 =0, весовые коэффициенты суперпозиции c s = 1 / ( n s !)^1/2, s = 1,2,3 (для выравнивания энергии пучков).

Согласно теории топологический заряд должен быть равен 4, 2, 1 на тех рисунках, на которых красное кольцо является соответственно внешним (рис. 4 а , б , д , е ), средним (рис. 4 в , г , и , к ), внутренним (рис. 4 ж , з , л , м ). При численном расчёте по мгновенным распределениям фазы с рис. 4 по формуле М.В. Берри (3) вдоль окружности радиуса R 1 ≈ 5 мм были получены значения 3,996 (рис. 4 а , б , д , е ), 1,998 (рис. 4 в , г , и , к ), 0,999 (рис. 4 ж , з , л , м ), то есть расчёт подтверждает соответствующие теоретические значения. Кроме того, топологический заряд на распределениях фазы может быть определён и визуально. На рис. 4 б , е имеется по четыре оптических вихря порядка +1 и потому топологический заряд равен TC =4. На рис. 4 г , к в дополнение к четырём вихрям порядка +1 имеется два вихря порядка –1, то есть топологический заряд равен TC =2. На рис. 4 з , м таких вихрей порядка –1 уже по три, и потому топологический заряд равен TC = 1.

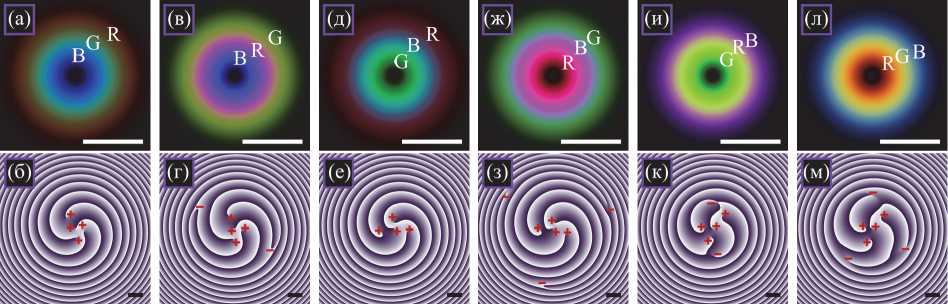
Рис. 4. Усреднённые распределения интенсивности (а, в, д, ж, и, л) и мгновенные распределения фазы (б, г, е, з, к, м) шести разных суперпозиций трёх однокольцевых пучков ЛГ разного цвета (λ 1 = 400 нм, λ 2 = 550 нм, λ 3 = 700 нм) на расстоянии z = z 2 / 2 ≈ 0,71 м (половина расстояния Рэлея пучка со средней длиной волны) в момент времени t = 60 с. Другие параметры расчёта: радиус перетяжки Гауссова пучка w = 500 мкм, топологические заряды n 1 = 1, n 2 = 2 и n 3 = 4 (а, б), n 1 = 1, n 2 = 4 и n 3 = 2 (в, г), n 1 = 2, n 2 = 1 и n 3 = 4 (д, е), n 1 = 2, n 2 = 4 и n 3 = 1 (ж, з), n 1 = 4, n 2 = 1 и n 3 = 2 (и, к), n 1 = 4, n 2 = 2 и n 3 = 1 (л, м), радиальные индексы p 1 = p 2 = p 3 = 0, весовые коэффициенты суперпозиции c s = 1 / (n s !)^1/2, s = 1, 2, 3 (для выравнивания энергии пучков). Масштабная метка на каждом рисунке показывает 1 мм. Тёмный и светлый цвет на распределениях фазы означает соответственно 0 и 2π. Символы ‘R’, ‘G’ и ‘B’ (а, в, д, ж, и, л) показывают области доминирования соответственно красного, зелёного и синего пучка. Красные символы ‘+’ и ‘–’ на распределениях фазы показывают оптические вихри порядков +1 и –1

Заключение

В работе рассмотрены разные варианты осевой когерентной суперпозиции пучков Лагерра–Гаусса с разными длинами волн. По известной формуле Берри рассчитан топологический заряд осевой суперпозиции двух пучков Лагерра–Гаусса разных «цветов», у каждого из которых своя длина волны и разный ТЗ.

Оказалось, что ТЗ такой суперпозиции равен ТЗ пучка ЛГ с большей длиной волны, независимо от величины весового коэффициента этого пучка в суперпозиции и от величины его ТЗ. Этот расчет ТЗ можно обобщить на суперпозицию произвольного конечного числа пучков ЛГ с разыми длинами волн, как однокольцевых, так и многокольцевых. При этом ТЗ всей суперпозиции будет равен ТЗ того пучка ЛГ, у которого длина волны больше. Этот результат подтвержден численно для суперпозиции из трёх пучков и для суперпозиции трехкольцевых пучков. Из-за того, что фазовые скорости пучков разные, распределение интенсивности в сечении пучка будет меняться со скоростью, пропорциональной разности максимальной и минимальной длин волн. При этом мгновенный ТЗ такой суперпозиции сохраняется, а распределение интенсивности (усредненное по времени) «цветного» оптического вихря меняет свою световую «гамму». Например, для двухцветной суперпозиции, если в ближней зоне с ростом радиуса цвета световых колец (радуга) меняются согласно их ТЗ в суперпозиции от меньшего к большему, то при распространении в пространстве (в дальней зоне) с ростом радиуса цвета колец в радуге располагаются в обратном порядке от большего ТЗ к меньшему. Показано также, что специальным подбором длин волн (синего, зеленого и красного) в трехцветной композиции однокольцевых пучков ЛГ можно получить на некотором расстоянии усредненное по времени световое кольцо белого цвета.

Заметим, что, хотя при распространении суперпозиций параксиальных световых полей в свободном пространстве могут появляться или исчезать дополнительные вихри [14], в непараксиальном случае ТЗ при распространении сохраняется [15]. Поэтому при малых радиусах перетяжки, сравнимых с длиной волны, пучок распространяется непараксиально, но полученные выражения для ТЗ должны оставаться верными. Но, так как пучки Лагерра–Гаусса аналитически описываются в параксиальном приближении и для оптической передачи информации практический интерес представляют только параксиальные пучки, численное моделирование в работе выполнено в параксиальном приближении.

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) (параграфы «Топологический заряд суперпозиции двух цветных оптических вихрей», «Топологический заряд белого оптического вихря»), а также Министерства науки и высшего образования РФ в рамках выполнения работ по

Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (параграф «Моделирование»).