Коэффициент диффузии хрома и ближний порядок в сплавах Fe-Cr

В связи с обнаружением [1,2] у ОЦК «-сплавов Fe-Cr начального участка концентраций хрома, для которого энергия смешения компонентов £См имеет отрицательный знак, представляется интересным обсудить концентрационную зависимость коэффициента диффузии хрома. Дело в том, что уравнение Даркена [3]

Ясг=Д>(1 + ^^Д           (О

Cr с\ Slnx У связывающее парциальный коэффициент диффузии компонентов (здесь хрома) с производной

----L, где f - коэффициент активности компо-Э1пх/ нента i в растворе с железом, ах,- его концентрация (в атомных долях), может быть легко преобразовано [4] к виду, содержащему энергию смеше

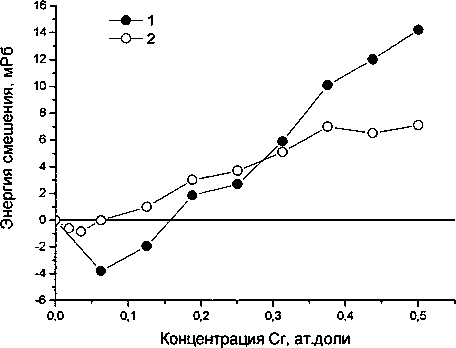
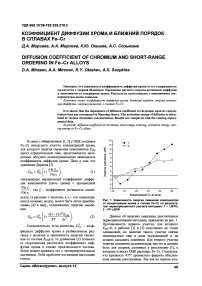
Рис. 1. Зависимость энергии смешения компонентов от концентрации хрома в сплаве Fe-Cr по результатам первопринципного расчета методами: 1 - LMTO; 2-FPLAPW

ния:

^Сг ” ^Сг

х(1 х) а £см

RT дх2

Следовательно, если известны D*_Cr - коэф

фициент диффузии хрома в разбавленном растворе с железом и зависимость энергии смешения от состава E_CmW, то уравнение (2) позволяет теоретически рассчитать коэффициент диффузии хрома в сплаве произвольного состава. Затем можно сравнить его с экспериментальным значением. Этой проблеме посвящена настоящая статья.

Данные об энергиях смешения, рассчитанные первопринципными методами, приведены на рис. 1. Протяженность первого участка, для которого ^см<0, в работах [1] и [5] получилась не точно одинаковой, но наличие такого участка сейчас подтверждено еще в ряде исследований и не должно вызывать сомнения. Для второго участка энергия смешения положительна, как это и должно быть для сплавов, склонных к расслоению [1], к которым относят ОЦК растворы Fe-Cr. Считается, что хрупкость 475° хромистого феррита обусловлена именно расслоением. Так как на первом уча-

стке кривая вогнута вверх, то ----- > 0 (разуме-

8xz ется, между точками перегиба). Тогда из уравнения (1) следует, что коэффициент диффузии хрома должен возрастать с ростом концентрации х. Напротив для участка II, где кривая £cmW вогнута вниз, а вторая производная---< 0, коэффици-8х2

ент диффузии должен уменьшаться с увеличением содержания хрома.

Рассмотрим экспериментальные данные [611] для коэффициента диффузии хрома, представленные на рис. 2.

выражения для коэффициентов диффузии. Применительно к сплавам Fe-Cr формулы Маннинга имеют следующий вид:

'  х(1-х)82Есм t RT 8х2

iji-x^-D^ '

^Cr

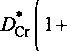
х(1-х) S2^

RT бх2 .

(За)

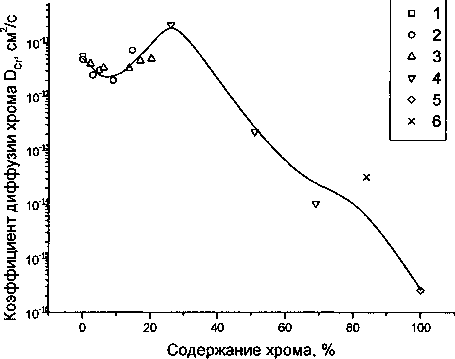
Рис. 2. Влияние концентрации на коэффициент диффузии хрома в сплавах с железом при 7=1073 К по данным 1 - [6]; 2 - [7]; 3 - [8]; 4 - [9]; 5 - [10]; 6 - [11]

где Мо=5,33 [4, с. 279] для ОЦК кристаллов.

Если х=0, то D_Cl = Ь^_т, а при х -»1

D_Fe = П^_е . Таким образом, D*_Ct и D^_e представляют коэффициенты диффузии атомов хрома в железе и атомов железа в хроме, когда они образуют разбавленные растворы. Если принять, что коэффициенты диффузии D^_T и D^_e не зависят от

состава, то при х=0 D_Fe = D_¥e

Г 2^-^))

1+—---;—-

М0^е

Следовательно, коэффициент диффузии железа не переходит и в теории Маннинга в коэффициент самодиффузии железа; а при х=1 коэффициент

диффузии хрома D_Cl = D^_T

Характер изменения D_Ct оказался почти зер

Л^Сг

так

кально отраженным по отношению к ожидаемому. Вместо начального возрастания и максимума величины D наблюдается ее снижение до минимума с последующим возрастанием для второго участка. Но и там возрастание не простирается до х=1. Наблюдается максимум значений D_Ct в районе 25 ат. %, а затем снижение, обусловленное, вероятно, тем, что коэффициент самодиффузии хрома Z>q,

же не переходит в коэффициент самодиффузии хрома. Основываясь на данных [11] о диффузии

меченых атомов, можно принять

(в хроме) = 0,47 ехр

-79 300

RT

(в железе) = 2,33 ехр

-57 070^ . RT J

, см2/с.

равный по [11] Dq_t =0,2 8 exp

73 850 ^

RT J

, резко

Различие этих величин столь велико, что в формулах (За, 36) можно пренебречь слагаемым (l-x)Dp_e в знаменателе и D^_e в числителе. Тогда

отличается от коэффициента диффузии хрома в очень

разбавленном

D^ = 2,33 ехр

растворе в железе:

^Сг

= ^г

57 070^

RT J

см2/с[11],хотя согласно

x(l-x)d²£_CM Y₁ 2х"

_< RT дх² Д ^о.

(2) и при х -> 0 и при х -> оо коэффициент диффузии хрома должен стремиться к D_Cl . Таким об

разом, формула Даркена, отражающая термодинамический эффект легирования, плохо согласуется с данными экспериментов по диффузии хрома в Or железо. Маннинг [12] дополнительно учел, что диффузия атомов в растворе замещения происходит с помощью вакансий, и получил более точные

Таким образом, первая поправка Маннинга не меняет теоретического характера изменения коэффициента диффузии хрома.

Интересно рассмотреть концентрационную зависимость энергии активации диффузии Q по экспериментальным данным [5, 7-10, 13] (рис. 3), так как изменение коэффициента диффузии

DCr=Doexp(-^),

при возрастании содержания хрома обусловлено,

Мирзаев Д. А., Мирзоев А.А., Оки шее К.Ю., Созы кина А.С.

прежде всего, изменением энергии активации. Она возрастает примерно до 6 % хрома, затем, перейдя через максимум, начинает уменьшаться до содержания 27 ат. %. Затем наблюдается новый сильный подъем энергии активации до максимума в районе х_Сг⁼0,7, а далее новое снижение, минимум и очередной подъем вплоть до чистого хрома. Маннинг считает, что изменение концентрационной зависимости энергии активации диффузии для постоянной температуры может быть связано с сильной температурной зависимостью еще одного введенного им корреляционного множителя ф . Он оказывает существенное влияние на коэффициент диффузии, если атомы разного сорта сильно отличаются по частоте обмена местами с вакансией; быстродиффундирующие атомы будут многократно обмениваться местами с вакансией, удерживать ее практически на одном месте. Оговорив значительное влияние ближнего порядка на коэффициент диффузии, Маннинг приводит выражение для Ф в случае неупорядоченного раствора [12], которое для системы Fe-Cr имеет следующий вид:

(Мо +2)((1-х)£^е +xDcr)-2£>cr =-----------------;-----------------------г-----, (6)

(^о + 2) ((1 - х) В^_е + xZ>cr)

но в силу огромного различия между D*Cx и Dpe множитель ^Сг =----— и от температуры не за-

М_о +2

висит.

Таким образом, учет второго множителя Маннинга также не может объяснить концентрационную зависимость D_Cl и энергии активации.

В ходе проведенного анализа мы считали, что величины Dq и z£_e остаются независящими от концентрации. Теперь становится ясным, что они должны существенно изменяться с повышением концентрации хрома. В работе [3] отмечена корреляция между энергией активации диффузии данной примеси и температурой плавления сплава:

бсг⁼^пл Fe ^XFe ⁺ _RTCr ^ХСт ’        О)

где Тпд - температура плавления сплава, a Qq и Q^ - энергии активации диффузии атомов хрома в железе и хроме (самодиффузия). М.А. Штремель также подтверждает существование подобной связи [14]. Он приводит для хрома значение

.......—” = 24,8, откуда следует, что энергия актива ции само диффузии хрома ^г =105,3 ккал/моль. В тексте монографии [14] отмечается существование излома на температурной зависимости коэффициента самодиффузии хрома, в силу чего существуют два значения энергии активации. Од

73 850^ RT J

нако уравнение 0,28 ехр -

[11] относит

ся именно к высокотемпературной ветви зависимости D^x = ДТ). Поэтому в данной работе при- йсг 73700

нято значение—— =-----= 17,34, а тогда для

RT^ 2136R диффузии в неупорядоченных сплавах Fe-Cr: 6Cr=7?TnjI(15,88(l-x) + 17,34x).         (8)

Расчеты по этому выражению были проведены в предположении, что 7^ есть температура солидуса сплава. Результаты расчетов сравниваются с экспериментальными на рис. 3.

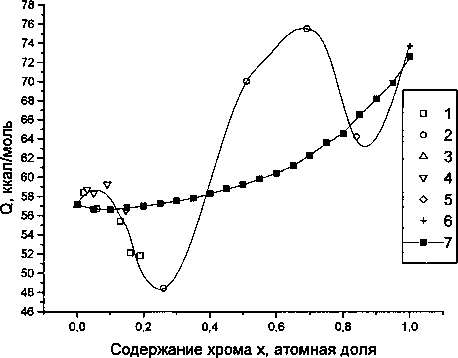
Рис. 3. Зависимость энергии активации диффузии Q от концентрации хрома в сплаве Fe-Cr. Экспериментальные данные: 1 - [8]; 2 - [9]; 3 - [5]; 4 - [7J; 5 - [10]; 6 - [13]; 7 - расчет по выражению (8)

В области концентраций, близких к х=1, совпадение результатов для Q неплохое. При малых концентрациях расчетные значения Q расположены ниже экспериментальных, но в области концентраций 0,12<х<0,37 экспериментальные значения энергии активации расположены существенно ниже расчетных, а в интервале 0,37<х<0,8 наблюдается противоположная ситуация. При этом необходимо обратить внимание, что оба отмеченных интервала принадлежат к той области концентраций хрома, где наблюдается ближний порядок типа расслоения. Таким образом, влияние ближнего упорядочения на энергию активации и коэффициент диффузии оказалось очень сложным. Несомненно, что наблюдающиеся отклонения экспериментальных значений энергии активации от результатов расчета по уравнению (8) связаны со специфической концентрационной зависимостью коэффициента корреляции в условиях сильного ближнего порядка, поэтому дальнейшей задачей исследования должен быть анализ эффекта корреляции перескоков атомов разного сорта.

Работа поддержана грантами РФФИ 07-0396021, НШ - 643.2008.3 и грантом АВЦП «Развитие научного потенциала высшей школы» 2.1.1/1776.