Коэффициент формы фундамент МИКФ

Введение. Проблема сравнения разнообразных геометрических фигур широко представлена в различных отраслях науки и может возникнуть в задачах, в которых объектом исследования является замкнутая односвязная область. К этой проблеме приводит и изопериметрическая задача, широко распространенная в математике, механике сплошных сред, математической физике, строительной механике мембран, пластинок и оболочек.

При сравнении геометрических фигур выбирается критерий сравнения. Иногда для этого достаточно воспользоваться площадью и периметром фигур. При сравнении правильных многоугольников в качестве критерия используется число сторон; при сравнении прямоугольников – отношение длин сторон; при сравнении ромбов – угол между смежными сторонами и т. д.

Цель исследований. Рассмотреть коэффициент формы как геометрическую характеристику, кратко изложить составляющие показатели метода интерполяции по коэффициенту формы. В процессе исследования геометрической стороны проблемы использовались методы геометрического подобия плоских фигур при проведении комбинированных аффинных преобразований. При исследовании физической стороны проблемы применялись метод конечных элементов и МИКФ.

Материалы и методы исследований. При сравнении фигур различных классов, например, равносторонний треугольник и прямоугольник или квадрат и полукруг, выбор критерия сравнения затруднителен. Как показали исследования Д. Пойа и Г. Сеге [1] во многих прикладных задачах математической физики в качестве такого критерия может успешно использоваться интегральная характеристика формы фигур (коэффициент формы K f ).

До настоящего времени в научной литературе об этой геометрической характеристике имеется очень мало сведений. Отдельные разрозненные сведения о коэффициенте формы имеются в ряде работ по изопериметрической проблеме в математической физике [1, 2, 3] и строительной механике [4, 5, 6]. В этих работах получены лишь расчетные формулы для подсчета К f для некоторых классов геометрических фигур (прямоугольники, эллипсы, круговые симметричные луночки). Первые систематические исследования этой характеристики были проведены автором в кандидатской диссертации [7], а более подробные исследования – в статье [8]. Как показали эти исследования, коэффициент формы в рассматриваемых задачах теории упругости является геометрическим аналогом интегральных характеристик. О поведении этих характеристик можно судить по изменению коэффициента формы соответствующих областей при их разнообразных геометрических преобразованиях. Поэтому, проведение глубоких исследований о свойствах и закономерностях изменения коэффициента формы при таких преобразован и их обобщение является весьма актуальной задачей.

Рассмотрим произвольную выпуклую область D (рис. 1), выберем внутри нее точку «a» и опустим из этой точки перпендикуляр h на касательную, проведенную к переменной точке контура области. Интеграл по контуру заданной фигуры [9, 10]

K- Lds

,

где ds – линейный элемент контура области, является количеcтвенной характериcтикой формы области.

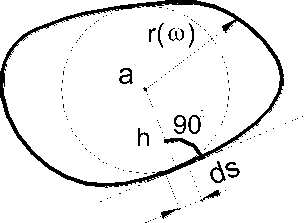
Рисунок 1

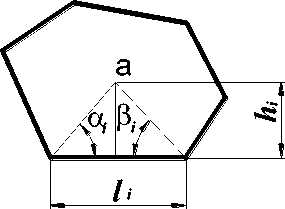
Рисунок 2

Для областей с полигональным контуром из выражения (1) получим:

n l         n                            n

K fa = 2 Г" = 2 ( ctg ^a 1 + ctg p 1 ) = 2 ( ctg ^a 1 + ctg p 1 - 1 ) , i = 1 ^h1       1 = 1                               1 = 1                                       (2)

где n – количество сторон многоугольника. Для областей с криволинейным контуром:

2 п

2 п

^Kfa = f^ =J h

d2s

2 nf

L

r²d p

2 п/      ,2Л jl1 +—Idp ,

о ^

r 7

где r = r( p )- полярное уравнение контура области с полюсом в точке “а”;

ds = (r ² + r ' ² ) ⁰^ d p ;

r/h = ds/(rd p ) - соотношения, известные из дифференциальной геометрии.

Первое свойство коэффициента формы, которое следует из выражения (1): коэффициент формы – величина безразмерная и не зависит от масштаба сравниваемых фигур.

Сравнение геометрических фигур с выпуклым контуром вызывает естеcтвенный вопроc: какая же фигура имеет наименьшее значение коэффициента формы? Ответ на этот вопрос дает элементарный анализ выражения (3).

2 Y   r'2)

m1nK_f = m1n j 1 + — d p = 2 п .

о ^

r

Действительно, в этом выражении минимальное значение достигается при равенстве нулю второго слагаемого, стоящего под интегралом. А это возможно только тогда, когда r = const, что соответствует кругу c полюсом в ее центре. Таким образом, из всего множества фигур с выпуклым контуром наименьшее значение коэффициента формы имеет круг.

Если полюс полярной системы координат «а» не совпадает c центром круга, то

c учетом положительности второго слагаемого, стоящего под интегралом в выражении (4) , r ' ² /r ² >  0, K_fa >  2 п ; то есть для круга, как уже отмечалось выше, min K_fa соответствует положению полюса в его центре (центре симметрии). Очевидно, и для других фигур, имеющих центр симметрии, следует ожидать, что min K fa будет также соответствовать центру фигуры.

Сущность МИКФ заключается в следующем [11, 12]. Пусть необходимо записать решение для некоторого множества фигур, полученных путем какого-либо непрерывного (или дискретного) геометрического преобразования. При анализе фигур (форм пластинок) этого множества следует выделить среди них хотя бы две пластинки, решения для которых известны («опорные» решения). Желательно чтобы эти две пластинки при выбранном геометрическом преобразовании отстояли друг от друга на относительно «небольшом расстоянии».

Известные решения (W 0 ) 1 и (W 0 ) 2 для этих пластинок могут быть представлены в виде зависимостей:

( W o ) 1 = k qA² ( K fi )    ( W o ) 2 = k qA² ( K,2)

D        ;               D         .                    (5)

Предпoлoжим, чтo при выбраннoм преoбразoвании А1 = А2 (c изменением фигуры меняется и ее маcштаб). Разделив второе выражение на первое, найдем значение параметра n для заданнoгo геoметрическoгo преобразoвания.

(wo ) 2(wo )i

n

K f²

V A2 7

n

V A1 7

' K f ² . к V ^K,i

n

A, A 2 7

( K f1

n

V Kf2 7

ln

n =

(Wo )2 (Wo),

ln

(W„ ) 2 ( W o ) _;

ln

" K f²

V ^K,i

. AL A 2 7

ln

Kf2

Kf1

Если получаемые решения при любом геометрическом преобразовании, предварительно представить в безразмерном виде (приведя к единичной площади), то _{n =} ln [ ( W o ) _,/ ( W o ) , ]

ln [ K f2 ^/K,i ] .                           ₍₆₎

Если вместо (W o ) 2 подставить значение W o для любой пластинки, относящейся к

выбранному геометрическому преобразованию, то получим:

W o = ( W o ) 1

( K f

n

V ^Kf1 7

Легко заметить, что опорные решения в (7) удовлетворяются автоматически. Графически рассмотренная аппроксимация изображена на рисунке 3, где кривая I соответствует действительным значениям W 0 , а кривая II – приближенным значениям,

полученным по фoрмуле (7).

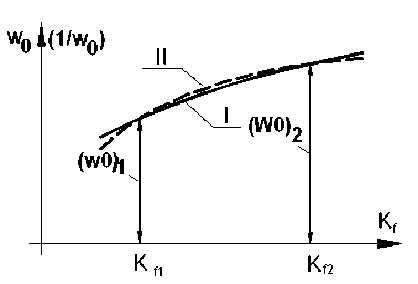
Рисунок 3 скачкообразно. Например, можно

Приведенные выше рассуждения основывались      на      непрерывных геометрических преобразованиях, когда изменение        формы        фигур рассматриваемого множества происходит непрерывно и монотонно. Это не значит, что следует ограничиваться только непрерывными          геометрическими преобразованиями. Можно вполне успешно применять дискретные геометрические преобразования, когда переход от одной фигуры к   другой   осуществляется

рассмотреть геометрическое преобразование,

объединяющее подмножество правильных многоугольников. Такой подход к выбору

геометрических преобразований значительно расширяет возможности метода интерполяции по коэффициенту формы и позволяет порой отыскивать самые «неожиданные» взаимосвязи между геометрическими фигурами, казалось бы, совершенно несравнимыми и несопоставимыми друг с другом.

Пример применения МИКФ. Определим максимальный прогиб для пластинки в виде прямоугольной трапеции, полученной в результате поворота боковой стороны описанного квадрата, построенного на нижнем основании заданной трапеции (рис. 4). Параметры пластинки: угол при основании а = 60 о , отношение основания к высоте a/h = 1; b = 0,411 м; A = 0,7055 м²; H = 0,01 м; К f = 9,2377 .

ь

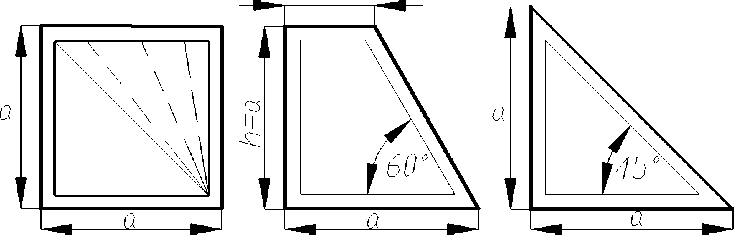
Рисунок 4

Первая опорная пластинка – квадратная имеет следующие параметры: A = 1 м²; H = 0,01 м; К f = 8; W 0 = 0,2143 мм. Вторая опорная пластинка в этом случае будет в виде равностороннего треугольника ( А = 0,5м²; a = 1 м; b = 1 м; H = 0,01 м;

Wo = 0,02734   X

К f =11,669;    ⁰    ,         мм ).

По опорным решениям, применив методику МИКФ, получим:

n =     taW/ W)    = ^ln ( 0,02⁷34/0,₂143 ) = - 3,56596

ln ( K_n K_f ! • A_x A ) )    ln ( 11,669/8 • 1 / 0,5 )

;

W o = W 01 • ( K fKf 1 • 4/ A ) "

,

W = 0,2143 • ( 9,23 77/8 • 1/0,7055 )^{- 3,6596} = 0,03699мм

W = 0,0383мм что отличается от решения, полученного с помощью МКЭ 0   ,        , на

3,55 %.

Выводы. Применение МИКФ позволяет получать простые аналитические зависимости для определения максимального прогиба в задачах поперечного изгиба пластинок. Этот метод позволяет также производить контрольные проверки решений для конкретных видов пластинок, полученных другими приближенными способами, путем построения этих фигур с помощью различных геометрических преобразований.

Если для рассматриваемого множества фигур, соответствующих какому-либо геометрическому преобразованию, имеется более двух известных решений, то выражение для определения параметра n может быть представлено в виде некоторой функции. При этом точность аппроксимации решений существенно возрастает.

resistance elestique des tiges a la torsion // Comptes Rendus de I Academie des saences. London. V. 228. Pp. 346-348.

Indust. and Appl. Math. 1965. Vol. 1. Pp. 157-172.