Коэффициент поперечной деформации и нелинейность силы межатомного взаимодействия

Автор: Мантатов В.В., Бадмаев С.С., Сандитов Д.С.

Журнал: Вестник Бурятского государственного университета. Химия. Физика @vestnik-bsu-chemistry-physics

Статья в выпуске: 1, 2017 года.

Бесплатный доступ

Рассмотрена взаимосвязь параметра Грюнайзена и коэффициента Пуассона (ко- эффициента поперечной деформации) кристаллических и стеклообразных твер- дых тел. Показано, что коэффициент Пуассона µ однозначен функции параметра Грюнайзена γD. Сопоставление результатов расчетов показывает однозначную связь между гармоничной и ангармоничной γD величины, что не характерно для теории упругости.

Ангармонизм колебаний решетки, коэффициент пуассона, параметр грюнайзена, теория упругости, поперечная деформация, межатомное взаимодействие

Короткий адрес: https://sciup.org/148316668

IDR: 148316668 | DOI: 10.18101/2306-2363-2017-1-31-36

Текст научной статьи Коэффициент поперечной деформации и нелинейность силы межатомного взаимодействия

Коэффициент Пуассона ц , который иногда называют коэффициентом поперечной деформации, по определению равен отношению относительной поперечной деформации тела e z = A r/r к его относительному продольному удлинению e x = A l/l при одноосном растяжении

A r/r Ц =--©.

A l/l

Согласно работе [1], у изотропных твердых тел диапазон разрешенных значений ц определяется по известной формуле теории упругости из условия положительности упругих модулей (B > 0, G > 0)

1 ( 3 B - 2 G / Ц ⁼

21 3 B + G /

В соответствии с этим соотношением при равенстве нулю модуля объемного сжатия B = 0 коэффициент Пуассона равен нижнему пределу ц =

-1, а когда модуль сдвига равен нулю G = 0, получаем верхний предел ц = %.

Таким образом, по Ландау и Лифшицу величина µ может меняться в интервале

- 1 ≤ µ ≤0.5

Разберем связь коэффициента поперечной деформации µ с параметром Грюнайзена γ D , который входит в уравнение состояния твердых тел и служит мерой ангармонизма колебаний решетки и нелинейности силы межатомного взаимодействия. Грюнайзен вывел формулу:

β BV

Yd = ^, CV

с помощью которой можно вычислять γ D из экспериментальных данных о коэффициенте объемного теплового расширения β , изотермическом модуле объемного сжатия В , молярном объеме V и молярной теплоемкости C V .

Наряду с уравнением Грюнайзена (4) предложены другие способы расчета γ D . Опираясь на теорию упругости, молекулярную акустику и термодинамику, Леонтьеву [2] удалось усреднить частоту колебаний решетки и непосредственно из определения параметра Грюнайзена вывести следующее соотношение для величины γ D

( о Л B A

Yd = 2l o^ Г2 к рик 7

где B A — адиабатический модуль объемного сжатия, ρ — плотность, υ К — средняя квадратичная скорость, квадрат которой является инвариантом суммы квадратов скоростей распространения продольных ( υ L ) и поперечных ( υ S ) упругих волн

υ _К

2 _ ^u l + 2 ^u ₅

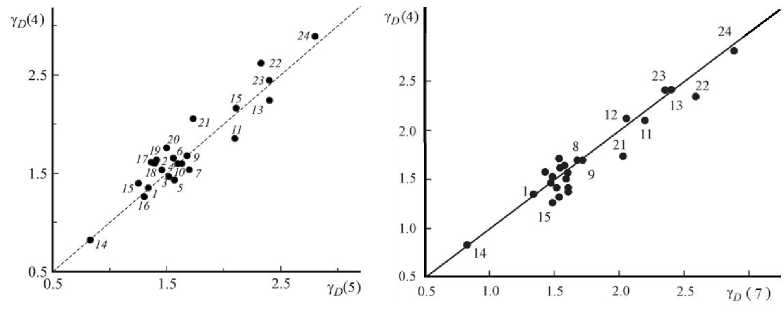
Рис. 2. Сравнение значений параметра Грюнайзена, рассчитанных по уравнению Грюнайзена γ _D (4) и по формуле Беломе-стных-Теслевой (7). Номера точек соответствуют номерам твердых тел в табл. 1.

Рис. 1. Сравнение значений параметра Грюнайзена, рассчитанных по уравнению Грюнайзена γ _D (4) и по формуле Леонтьева γ _D (5). Номера точек соответствуют номерам твердых тел в табл. 1.

Таблица 1

Сопоставление результатов расчета параметра Грюнайзена γ D по уравнениям (4), (5) и (7) [3, 4]

№	Элементы и соединения	µ	Параметр γ D по уравнению
№	Элементы и соединения	µ	Грюнайзена (4)	Леонтьева (5)	Беломестных- Теслевой (7)
1	LiF	0.214	1.34	1.35	1.34
2	NaCl	0.243	1.46	1.53	1.47
3	LiCl	0.245	1.52	1.47	1.48
4	KCl	0.259	1.60	1.60	1.54
5	NaF	0.234	1.57	1.44	1.43
6	NaBr	0.270	1.56	1.65	1.60
7	LiBr	0.256	1.70	1.53	1.53
8	KBr	0.283	1.68	1.67	1.67
9	Fe	0.292	1.68	1.68	1.72
10	KI	0.265	1.63	1.60	1.57
11	Co	0.357	2.10	1.85	2.19
12	Al	0.340	2.11	2.16	2.05
13	Ag	0.379	2.40	2.24	2.40
14	Be	0.034	0.83	0.83	0.82
15	Y	0.245	1.25	1.40	1.48
16	NaNO 3	0.257	1.31	1.27	1.53
17	NaClO 3	0.270	1.37	1.61	1.60
18	Th	0.254	1.40	1.61	1.52
19	Mg	0.270	1.41	1.64	1.60
20	RbBr	0.267	1.50	1.76	1.59
21	Ta	0.337	1.73	2.05	2.03
22	AgBr	0.396	2.33	2.65	2.58
23	Pd	0.374	2.40	2.44	2.35
24	Au	0.420	2.80	2.90	2.88

На рис. 1 сопоставляются результаты расчета γD по уравнениям Грюнайзе-на (4) и Леонтьева (5) для ряда твердых тел (табл. 1) [3]. Как видно, наблюдается удовлетворительное согласие между этими соотношениями. Отклонения от данной корреляции для некоторых твердых тел обусловлены, по-видимому, главным образом разбросом значений γD, полученных разными исследователями.

Используя выражение для модуля сдвига G = ρν S² и формулу (6) для ν K² , преобразуем уравнение Леонтьева (5)

3 ( Вл ) и 2 3 (Вл 3

Yn = —I —— I = -А ----------.

21PUS J иК 2 V G JUl/vs )2 + 2

Далее, с помощью известных выражений теории упругости [1]

B = 2 — 1 f-I = 2-2^ 1G 3 V1 - 2ц J V US ) V 1 - 2Ц J в приближении A приходим к формуле Беломестных-Теслевой [10]

Таблица 2

Упругие свойства и параметр Грюнайзена натриевоалюмосиликатных стекол (использованы данные [6])

№	Состав по синтезу, мол. %			ρ, 10^-3кг/м³	v L , м/с	v S , м/с	B , 10^-8Па	µ	γ D
№	Na 2 O	Al 2 O 3	SiO 2	ρ, 10^-3кг/м³	v L , м/с	v S , м/с	B , 10^-8Па	µ	γ D
1	15	0	85	2.339	5430	3340	342	0.196	1.28
2	15	5	80	2.358	5570	3390	370	0.206	1.31
3	15	10	75	2.410	5697	3510	386	0.194	1.26
4	15	15	70	2.465	5737	3469	416	0.212	1.34
5	15	20	65	2.428	5850	3540	425	0.211	1.34
6	15	25	60	2.472	6000	3568	470	0.226	1.40
7	25	0	75	2439	5280	3140	359	0.226	1.40
8	25	5	70	2.455	5480	3240	394	0.231	1.41
9	25	10	65	2.461	5610	3330	411	0.228	1.40
10	25	15	60	2.480	5640	3350	418	0.227	1.39
11	25	20	55	2.470	5680	3450	405	0.208	1.32
12	25	25	50	2.499	5790	3490	432	0.215	1.35
13	25	30	45	2.519	6026	3556	490	0.233	1.43
14	35	0	65	2.497	5340	3070	398	0.253	1.52
15	30	5	65	2.486	5500	3200	413	0.244	1.47
16	20	15	65	2.450	5670	3490	390	0.195	1.28
17	17.5	17.5	65	2.447	5746	3458	418	0.216	1.35

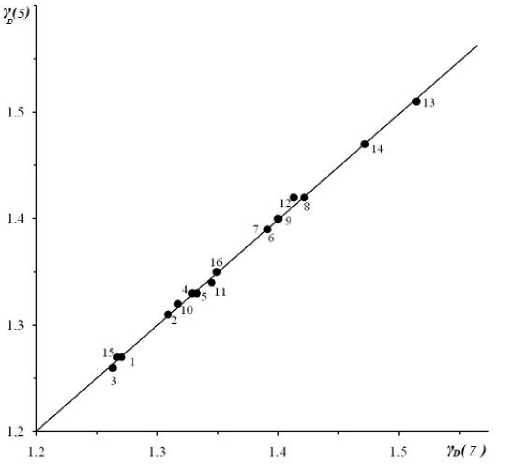
Рис. 3. Сравнение значений параметра Грюнайзена, рассчитанных по уравнению Леонтьева (5) и по формуле Беломестных-Теслевой (7), для натриевоалюмосиликатных стекол. Номера точек соответствуют номерам стекол в табл. 2.

3 । 1 + ц । yd =t| ~ P

2 V 2 - 3 ц )

которая была получена авторами [3] из иных исходных посылок.

Эта формула привлекательна тем, что позволяет рассчитывать γD по данным только о коэффициенте Пуассона µ. Оценка γD с ее помощью для многих металлов, ионных и молекулярных кристаллов удовлетворительно согласуется с расчетом по уравнению Грюнайзена (4) (табл. 1) [4, 5]. Рис. 2 подтверждает согласие между уравнениями Беломестных-Теслевой и Грю-найзена.

На рис. 3 приводится зависимость параметра Грюнайзена γ D , рассчитанного по формуле Леонтьева (5), от функции коэффициента Пуассона по Беломе-стных-Теслевой (3/2)(1+ µ )/(2-3 µ ) для натриевоалюмосиликатных стекол с различным содержанием окислов (табл. 2 [5]). Видно, что уравнения Леонтьева (5) и Беломестных-Теслевой (7) хорошо согласованы с экспериментальными данными. Такие же результаты получаются для других стекол.

Таким образом, коэффициент Пуассона µ оказывается однозначной функцией параметра Грюнайзена γ D .

Отмечая согласие формулы Беломестных-Тесловой (7) с уравнением Грю-найзена (4), необходимо обратить внимание на тот факт, что эта формула однозначно связывает между собой гармоническую (линейную) µ и ангармоническую (нелинейную) γ D величины, что не характерно для теории упругости.

Известны попытки качественного объяснения наличия взаимосвязи между линейными и нелинейными величинами [6].

Работа выполнена при финансовой поддержке Министерства образования РФ (грант № 1932).

Список литературы Коэффициент поперечной деформации и нелинейность силы межатомного взаимодействия

Ландау Л. Д., Лифшиц Е. М. Теория упругости. - М.: Наука. - 1965. - 204 с.
Леонтьев К. Л. О взаимосвязи между упругими и тепловыми свойствами твердых тел // Акустический журнал. - 1981. - Т. 47, Вып. 4. - С. 554-561.
Беломестных В. Н., Теслева Е. П. Взаимосвязь ангармонизма и поперечной деформации квазиизотропных поликристаллических тел // ЖТФ. - 2004. - Т. 74, Вып. 8. - С. 140-142.
Сандитов Д. С., Беломестных В. Н. Взаимосвязь параметра теории упругости и усредненный модуль упругости твердых тел // ЖТФ. - 2011. - Т. 81, Вып. 11. - С. 77-81.
Лившиц В. Я., Теннисон Д. Г., Гукасян С. Б., Костанян А. К. Акустические и упругие свойства стекол системы Na2O-Al2O3-SiO2 // Физика и химия стекла. - 1982. - Т. 8, № 6. - С. 688-693.
Сандитов Д. С. Коэффициент поперечной деформации стеклообразных твердых тел. Германия: международный издательский дом LAP Lambert Academic Publishing. - 2016. - 72 р.

Статья научная