Коэффициент Пуассона и упругие модули многокомпонентных оптических стекол

Представляет определенный интерес природа произведения плотности ρ на квадрат среднеквадратичной скорости волн деформации v_k ² [1, 2]

K = ρν k² ,                                                     (1)

где v k ² для кубических кристаллов является инвариантом суммы квадратов скоростей распространения продольных ( v L ) и поперечных ( v s ) акустических волн [3, 4]

Б.Д. Сандитов, М.В. Дармаев, Д.С. Сандитов. Коэффициент Пуассона и упругие модули многокомпонентных оптических стекол

v

2 k

vL + 2v2 3

Настоящая работа посвящена исследованию природы величины K и установлению связи K с упругими модулями и коэффициентом Пуассона применительно к оптическим стеклам.

Теоретическая часть

Обратимся к формуле для модуля объемного сжатия B кубических кристаллов

B _     11 ⁺ ~ 12

и к соотношению для квадрата среднеквадратичной скорости звука v k ² , представленному в виде [3, 4]

C + C

PV2 _    '13 44 , где С11, С12 и С44 – упругие постоянные 2-го порядка.

Из этих двух выражений видно, что при выполнении условия Коши: С ₁₂= С ₄₄, когда между однородно деформированными областями кубической решетки действуют центральные силы, величина K =ρ v k ² совпадает с модулем объемного сжатия K = B . Во всех других случаях произведение ρ v k ² отлично от B .

Убедимся, что, так же как и отношение упругих модулей изотропных тел, в частности, отношение модуля сдвига G к модулю объемного сжатия B [5],

G _ 3 f 2ц),(5)

B 2 ( 1 + ц J величины G/K и B/K являются однозначными функциями коэффициента Пуассона µ.

Разделив модуль сдвига G =ρ v s ² на рассматриваемую величину K =ρ v k ² , получаем соотношение

G _ v!.

Kv

С помощью формулы (2) правую часть данного равенства ( v_s ² / v_k ² ) выразим через отношение квадратов продольной и поперечной скоростей звука ( v L ² / v s ² )

v

v

S v L

2    3 _V2 ^{+ 2}

k V ^v s

- 1

где ( v L ² / v s ² ) у изотропных тел является функцией коэффициента Пуассона µ [5]

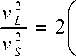
1 - ц

1 - 2 ц

Подставив (8) в выражение (7), а затем в соотношение (6), приходим к заключению, что отношение G / K является функцией только коэффициента Пуассона

G _ 3 f 1 ^{- 2} ц ^                                   (9)

K ~ 2 V 2 - 3 ц J

Из комбинации данной формулы с равенством (5) следует, что отношение B / K есть однозначная функция µ

B _ 1 + ^ц .                                        (₁₍

K 2 - 3 ц

Этот результат был получен ранее иным способом [1].

Таким образом, во-первых, как и модуль сдвига, величина K =ρ v k ² выражается через произведение плотности на квадрат скорости звука, и, во-вторых, при выполнении условия Коши она совпадает с модулем объемного сжатия. В-третьих, так же как и отношения упругих модулей, отношения G / K и B / K оказываются однозначными функциями коэффициента Пуассона. Величина K =ρ v_k ² , обладающая характерными признаками упругих модулей, была названа усредненным модулем упругости [1]. Это название является не совсем удачным, поскольку известные модули упругости E , G и B также относятся к усредненным характеристикам. Поэтому целесообразно назвать K эффективным модулем упругости (подошло бы также название: характерный упругий модуль).

При установлении зависимости B / K от коэффициента Пуассона в виде (10) были использованы соотношения для изотропных кристаллов с кубическими решетками. Тем не менее эта зависимость (10) оказалась оправданной для кристаллических твердых тел с другими решетками [1].

Сравнение с экспериментом. В работе рассмотрено применение выражения (10) к многокомпонентным промышленным оптическим стеклам. Необходимые экспериментальные данные взяты из [6-8]. Как видно из рис. 1, зависимость отношения B / K от функции коэффициента Пуассона (1+µ)/(2-3µ) является линейной, причем в соответствии с равенством (10) прямая проходит через начало координат с наклоном, равным единице, что подтверждает справедливость формулы (10) для оптических стекол.

Таким образом, взаимосвязь эффективного модуля упругости с коэффициентом Пуассона и модулем объемного сжатия в виде (10) оправдана для многокомпонентных оптических стекол.

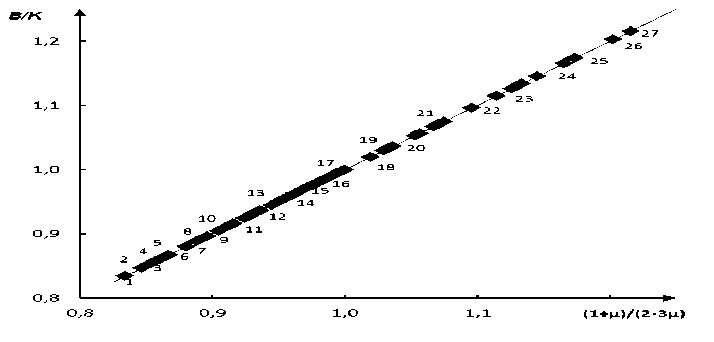
Рис. 1. Зависимость отношения модуля объемного сжатия к эффективному модулю упругости ( B / K )

от функции коэффициента Пуассона (1+µ)/(2-3µ) для многокомпонентных оптических стекол. 1 – ЛК7, 2 – КФ6, 3 – Ф6, 4 – КФ7, 5 – К14, 6 – ЛФ5, 7 – К8, 8 – КФ4, 9 – Ф13, 10 – К19, 11 – Ф4, 12 – ТФ1, 13 – БК6, 14 – БФ21, 15 – БФ8, 16 – БК10, 17 – ТФ7, 18 – ФК14, 19 – ТК13, 20 – ТК23, 21 – БФ11, 22 – ТК17, 23 – ОФ2, 24 – СТК7, 25 – СТК9, 26 – ЛК4, 27 – ТБФ4.

Данные взяты из [6-8]

Обсуждение результатов

Характерной особенностью эффективного модуля упругости K является его связь с параметром Грюнайзена γD, который служит мерой ангармонизма колебаний решетки и нелинейности силы межатомного взаимодейст- вия. Тесная связь между K и γD следует из сравнения соотношения (10) с формулой Беломестных – Теслевой [9]

3 I 1 + Ц Y D = T I T

,

2 ( 2 - 3 ц которая находится в соответствии с уравнением Грюнайзена [1, 9].

Как видно из равенств (10) и (11), эффективный модуль упругости определяется отношением модуля объемного сжатия к параметру Грюнайзена ( B /γ D )

K = ³ 1 B- ) .                                (12)

² I Y d J

При выполнении условия Коши B = K в данном выражении параметр Грюнайзена равен γ D =1.5. По уравнению (11) этому значению γ D соответствует коэффициент Пуассона µ=0.25. Величины γ D =1.5 и µ=0.25 характерны для ансамбля частиц с центральными силами взаимодействия. У натриевосиликатных стекол Na 2 O-SiO 2 при увеличении содержания окиси натрия Na 2 O (ионов натрия Na ⁺ ) от 0 до 30 мол.% µ и γ D возрастают от µ=0.17 и γ _D =1.2 до значений µ=0.25 и γ _D =1.5, присущих к структурам со сферически симметричным взаимодействием частиц [10]. При росте содержания ионов щелочных металлов R ⁺ (содержания R 2 O, R=Li, Na, K) в щелочноси-ликатных стеклах R₂O-SiO₂ возрастает степень ионности межатомных связей и происходит переход от сеточной структуры (у кварцевого стекла SiO 2 ) с направленными силами межатомного взаимодействия к преимущественно ионной разветвленной структуре с центральными силами взаимодействия ионов (у стекол R 2 O-SiO 2 ) [10].

Ангармонизм колебаний решетки и нелинейность силы межатомного взаимодействия проявляются, например, в пластической деформации стеклообразных твердых тел [11, 12]. Предел текучести σ y – напряжение, выше которого наблюдается пластичность стекла, – является функцией отношения модуля упругости E к параметру Грюнайзена E /γ D , аналогичного отношению B /γ D в равенстве (12) [11, 12]

1 I E " y  ⁶ 1 Y d

В процессе пластической деформации аморфных полимеров усиливается ангармонизм (растет γ D ) и снижаются потенциальные барьеры межмолекулярного происхождения в сравнении с недеформированным состоянием, которое характеризуется межмолекулярным взаимодействием, определяемым модулем упругости E [11, 12].

Из соотношений (12) и (13) следует, что у стеклообразных твердых тел, у которых µ≈const ( E / B≈ const), предел текучести пропорционален эффективному модулю упругости:

I ¹ - 2 ц V CT =             K .

y I 3 J

Н.А. Романов, А.В. Номоев, Г.М. Жаркова. Полимерно-дисперсные жидкие кристаллы, допированные наночастицами Ag, Cu, Si

По формулам (11)-(13) можно вычислять параметр Грюнайзена на основе данных только механических испытаний, тогда как по известному уравнению Грюнайзена величина γ _D рассчитывается главным образом по теплофизическим характеристикам. Можно убедиться, что эти формулы находятся в удовлетворительном согласии с уравнением Грюнайзена [1, 9].