Коэффициенты активностей компонентов зародышей продуктов химических реакций в сталеплавильных процессах

Неметаллические включения являются вредными примесями в стали. Поэтому изучению процессов образования и роста зародышей неметаллических включений всегда уделялось большое внимание [1–12]. Однако при изучении термодинамики роста зародышей неметаллических включений обычно не учитывалось отличие химических потенциалов компонентов наночастиц от химических потенциалов соответствующих макрообъектов. Ранее [13] нами была разработана методика расчета, учитывающая повышенные значения давления в нанофазах и зависимость поверхностного натяжения наночастицы от ее размера. Для зародышей сферической формы была получена формула m-1

ц nano = ц 0 ₊--- l ₊ _ £ ст j ( 5 j - X j ) + RT ln 4.                                        (1)

r r j =1

Здесь ц "ano - химический потенциал i -го компонента рассматриваемой наночастицы; m - число ее компонентов; r – ее приведенный радиус; X _j – мольная доля ее j -го компонента. Остальные величины относятся к макрофазе того же состава и при той же температуре T , что и рассматриваемая наночастица: ц ⁰ - стандартный химический потенциал i -го компонента; a i - активность i -го компонента; v – средний мольный объем; V_i – парциальный мольный объем i -го компонента; ст - коэффициент поверхностного (межфазного) натяжения; ст’ - производная коэффициента поверхностного натяжения по массе j -го компонента; R – универсальная газовая постоянная; 5 j - символ Кроненкера ( 5 j = 1 при i = j , 5 j = 0 при i ^ j ).

Считая для простоты, что активности компонентов в макрофазе, имеющей тот же состав и температуру, что и зародыш, равны их мольным долям, получим m - 1

ц nano = ц 0 +----L + _ £ CT j ( 5 j - X j ) + RT In X i .                                         (2)

r r _} = 1

Сравнивая это выражение с формулой nano 0           nano цi    =цi + RT ln ai   ,                                                                         (3)

где ainano – активность i-го компонента наночастицы зародыша (в отличие от ai из (1) – активности i-го компонента, в макрофазе, имеющей тот же состав и температуру, что и зародыш), заклю- чаем, что lnainano

i (             m - 1

=---- 2ст V - + 3 v V ст’(5.-- X j

rRT i £ j( J j)

k              j = ¹

+ In X i

и логарифм коэффициента активности f™™⁰ = a™"⁰ /Xi компонента зародыша равен

m - 1

ln f_i

nano

-I                       m -1

=---- 2стV- + 3vY ст',(5,, rRT i £ j( iJ k             J=1

k

- Xj )

Окончательно коэффициент активности i-го компонента зародыша равен f a = exp

1 rRT

2 ст V - + k

m - 1

3 v Ё£(5 -j j'=1

- Xj)

В качестве примера рассчитаем коэффициенты активности компонентов зародышей продуктов раскисления кислородсодержащего железа алюминием.

Зародыши продуктов раскисления кислородсодержащего железа алюминием

При введении алюминия в кислородсодержащее железо возможны (в зависимости от концентраций кислорода и алюминия) три варианта образования продуктов раскисления: образование включений глинозема Al 2 O₃, включений герцинита Al 2 O₃ • FeO и шлаковых включений переменного состава Al₂O₃ –FeO .

Рассмотрим наиболее сложный для расчета третий случай. При этом происходят химические реакции

2 [ Al ] +3 [ O ] = ( Al 2 O₃ ) ; [ Fe ] + [ O ] = ( FeO )

и образуются зародыши продуктов реакций. Зародыши растут, и на их поверхности протекают химические реакции. Растущие наночастицы состоят из раствора Al2O3 –FeO . Вблизи наночастицы концентрации компонентов расплава (Al, O, Fe) стремятся к локальному равновесию с концентрациями компонентов наночастиц.

Концентрации компонентов расплава вблизи частицы не равны объемным концентрациям в расплаве. Это вызывает диффузионные потоки компонентов, которые доставляют вещества для роста частиц. Таким образом, если мы хотим исследовать рост наночастицы, мы должны знать локальные равновесные концентрации компонентов расплава вблизи поверхности нано- частицы.

Чтобы определить равновесные концентрации, мы должны знать химические потенциалы компонентов растущих наночастиц. В нашем случае количество компонентов m = 2, индексы 1 и 2 обозначают Al2O3 и FeO соответственно. Для простоты предположим, что активности компонентов в макрофазе, идентичной по составу и температуре исследуемой наночастице, равны их мольным долям:

a А1 2 0 з = X А1 2 0 з ^;

a FeO = X FeO .

Обозначим долю оксида алюминия в частице через x (x = XA^O ). Теперь мы можем пере- писать уравнения (1) в виде fAao" = exp rR1T (и x) %о3 +3 v(x )^'(x )(1—x))

nano f FeO3 = exp

rRT ⁽ !’( ^x ) V FeO ,

- 3 xv ( x ) c ' ( x

Пусть температура составляет 1873 К. Мы использовали следующие значения [14]: ° Al 2 O₃ = 1,40 H/м; ° FeO = 0,18 H/м;

V A l₂O₃ = 3,433 - 10 — 5 м³/моль, V _FeO = 1,562 - 10 — 5 м³/моль.

Положим зависимость среднего мольного объема наночастицы от состава линейной: v = ( vA_hO - V_FeO ) x + V_FeO = 1,871 - 10 ^{- 5} x + 1,562 - 10 ^{- 5} ( м³/моль ) .

Также положим линейной зависимость поверхностного (межфазного) натяжения для макротела, имеющего тот же состав, что и рассматриваемый зародыш (наночастица) линейной:

° = (Aa| . O_; - ^ff FeO ) x + ^ FeO = 1,22 x + 0,18 ( H/м ) .                                              ⁽¹²⁾

Тогда

° ' = ( ° Al₂O₃ " ^ff FeO ) = ^1,22.                                                                         ⁽¹³⁾

Используя уравнения (9) с уравнениями (10)–(13), мы рассчитали химические потенциалы компонентов наночастиц (рис. 1, 2).

Рис. 1 показывает, что поверхностные эффекты оказывают существенное влияние на физикохимические процессы в зародышах лишь для частиц менее 100 нм. Для более мелких частиц их роль очень велика. Так, для частиц радиусом 1 нм коэффициент активности достигает для некоторых составов величин 0,926–1,2 для Al₂O₃ и 0,0057–1,42 – для FeO .

Рис. 2 показывает, как меняются коэффициенты активности компонентов наночастиц (зародышей) в зависимости от состава. Чем меньше частица, тем существеннее влияние поверхностных эффектов.

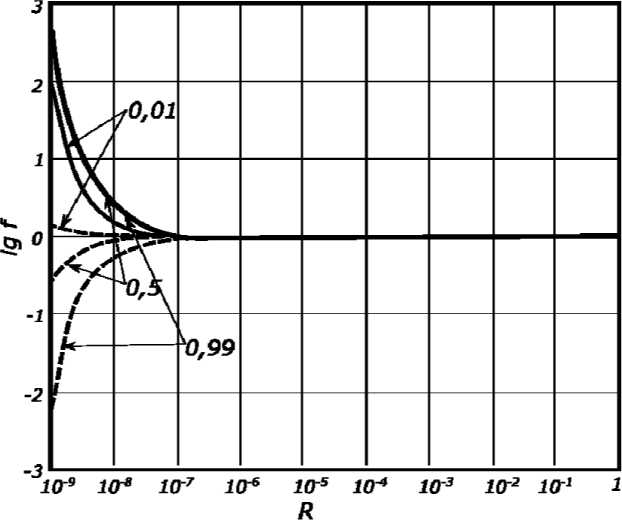
Рис. 1. Коэффициенты активности f компонентов зародышей Al₂O₃ – FeO в зависимости от их размера. Сплошные линии относятся к Al₂O₃ , пунктирные – к FeO .

Числа у кривых – доли Al₂O₃ в зародыше. R – радиус частицы, м

Fig. 1. The activity coefficients f of the components of the nuclei, depending on their sizes. Solid lines refer to Al₂O₃ , dotted lines refer to FeO . The numbers near the curves are the fractions Al₂O₃ in the nuclei. R is the radius of the particle, m

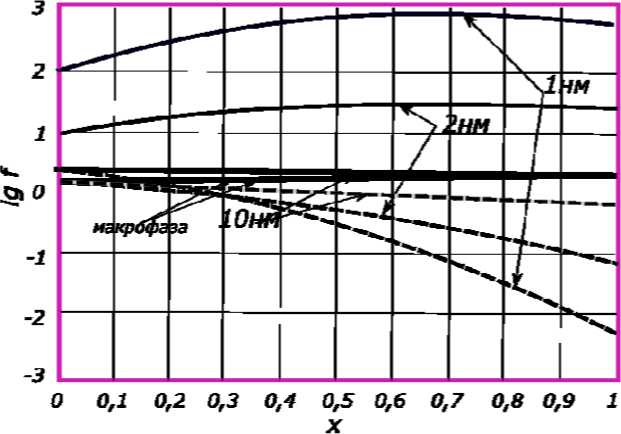
Рис. 2. Зависимости коэффициентов

Al₂O₃ – FeO различного размера от

активности f компонентов зародышей состава. Сплошные линии относятся к Al2O3 , пунктирные – к FeO . Числа у кривых – радиусы зародышей, x – доля

Al₂O₃ в зародыше

Fig. 2. The dependences of the activity coefficients f of the components of the nuclei Al₂O₃ – FeO of various sizes on the composition. Solid lines refer to Al₂O₃ , dotted lines refer to FeO . The numbers near the curves are the radii of the nuclei, x is the fraction Al₂O₃ in the nuclei

Выводы

• •    Поверхностные эффекты играют очень важную роль в поведении наночастиц. Результаты работы показывают, что они могут изменять активности компонентов наночастиц в ту или иную сторону в сотни раз. Применение обычных формул для расчета активностей компонентов в макрофазах недопустимо при исследовании взаимодействия наночастиц с окружающей средой, в частности, при изучении роста зародышей продуктов химических реакций.

• •    В работе приведена формула для расчета химических потенциалов компонентов наночастиц и показана ее важность.

• •    Влияние поверхностных эффектов на химические потенциалы мелких частиц важно только для частиц размером менее 100 нм.

• •    Формула (1) позволяет изучать измене-

• ния в составе растущих наночастиц. Она полезна для металлургии (образование неметаллических включений), аналитической химии (образование осадков), нанотехнологий (образование нанокристаллов в аморфных металлах) и других отраслей науки и техники.

• •    Предлагаемый метод может быть обобщен для анизотропных нанокристаллов и газовых пузырьков. Предлагаемый метод может быть скорректирован в зависимости от уровня наших знаний о свойствах наночастиц (физических и химических свойствах, поверхностном (межфазном) натяжении и других). Метод может быть использован, если мы знаем только средние значения требуемых свойств и если мы знаем их как функции переменных состояния. Чем точнее данные, которые мы используем, тем точнее будет результат.