Коэффициенты отражения и передачи слоистой среды и возможность определения комплексной диэлектрической проницаемости одного или двух слоев

При интерпретации данных полученных дистанционными методами необходимо знать комплексную диэлектрическую проницаемость (КДП) среды в широком интервале частот и температур. Для измерения КДП в диапазоне от 100 МГц до 20 ГГц используют ячейки в виде отрезков коаксиальных линий. В качестве измерителей применяют векторные анализаторы цепей, измеряющие матрицу коэффициентов рассеяния. Для восстановления КДП чаще всего используют модуль и фазу коэффициента прохождения, так как он измеряется точнее и процедура калибровки ячейки проще, чем при измерении коэффициента отражения [1–3]. Также применяется метод восстановления КДП с использованием модулей коэффициентов отражения и прохождения [4; 5]. Однако при проведении долгосрочных температурных измерений ячейки приходится подключать к прибору при каждой температурной точке по очереди. Это приводит к возрастанию времени измерения, так как необходимо ждать, пока в термостате снова установится нужная температура. Для повышения скорости проведения температурных измерений рассмотрена возможность определения КДП при подключении в тракт двух измерительных ячеек с различными образцами. При определении параметров нужно будет использовать и модули, и фазы коэффициентов отражения и прохождения, а также знать априорные значения КДП.

Образцы 2 и 6 (рис. 1) размещался между двумя шайбами из фторопласта 1, 3 и 5, 7. Диэлектрическая проницаемость фторопласта е = 2,05 ± 0,05 - j ■ 6 ■ 10-4. Средой 5, как и средами перед границей 1 и после границы 7, является воздух с диэлектрической проницаемостью е = 1 - j ■ 0. Комплексный коэффициент отражения (параметр S11) данной структуры от границы «воздух–шайба» (0–1) [6]:

7  — 7

S = Z вх1   Z 0

Z вх1 ⁺ Z 0

где

Z = Z вх2 + Z 1 th ( jk_xd j Z вх¹    Z 1 + Z вх 2 th ( jk i d j 1 ,

Z вх i вычисляются по аналогичным формулам:

Z _ Zвх^+1) + Zth(jkd) Z ™ Zi+ Z вх^+1) th (jkd) i, где i – индекс слоя; Zвх8 = Z8 = Z0, Z0 = 50 Ом – волновое сопротивление линии; ki = k0,Js"i - комплексное волно вое число i-го слоя, где еi - КДП i-го слоя; k0 = 2пf /c -волновое число в вакууме ( f – частота; с – скорость света); di - толщина i-го слоя; Zi = Z0 /-J^i . Комплексный коэффициент передачи (параметр S12) определяется как обратная величина произведения [6]:

¹ = T i T   ^Zi ^{+ Z} вх( i + 1)     - jk i d i

S П        , е

S 12     i = 0 Z ( i + 1) ⁺ Z вх ( i + 1)

где размеры d i показаны на рис. 1, кроме d 0 и d 8 , значения которых принимается равными нулю. Действительную ε′ и мнимую ε″ части КДП образца можно определять как из (1), так и из (2) методами оптимизации.

При проведении измерений использовались переходники для подключения разъема ZNB8 типа N к линии сечением 16/7. Для коррекции фазы коэффициента отражения необходимо определить физическую длину переходника, а затем вычислить фазу волны, которая набегает при прохождении волны до первой границы, и вычесть ее удвоенное значение из измеренных данных. Длину отрезка легко рассчитать, поставив перед слоем 1 короткозамыкатель, и измерив параметр S 11 . Для коррекции фазы коэффициента прохождения нужно определить физические длины переходников, рассчитать набегающую на них фазу и вычесть ее из измеренной фазы.

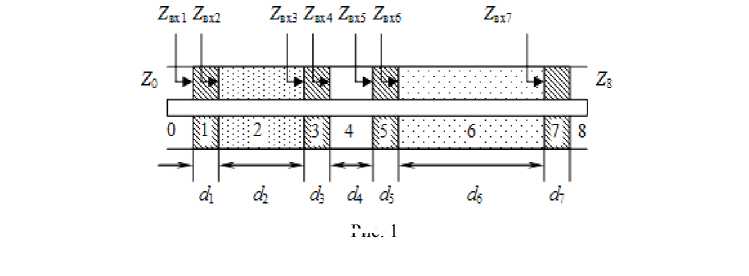
Рис. 1

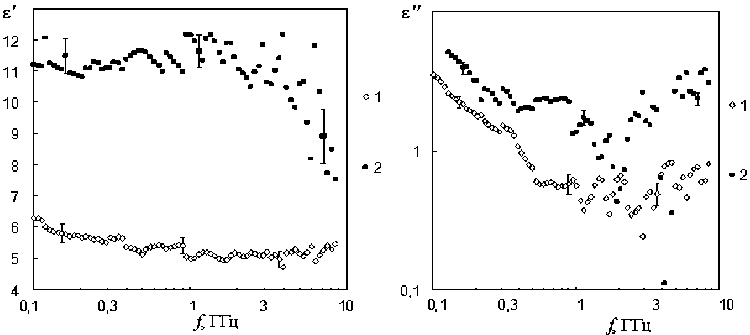
Рис. 3

Рис. 2

Методика расчета КДП одного образца аналогична, только нужно учитывать только три первых слоя, а для расчета достаточно взять или коэффициент отражения, или коэффициент прохождения. Априорные значения КДП на частоте 100–150 МГц определяются при помещении ячейки в бокс в разрыв центрального проводника коаксиальной линии. Метод измерения и расчета при таком подключении подробно приведен в [7].

Образцом был выбран речной песок с различной влажностью. В длинной ячейке находился образец объемной влажностью W об = 0,06 см³/см³, в короткой ячейке образец с W об = 0,22 см³/см³.

На рис. 2 приведены частотные зависимости действительной части КДП ε′ для образцов, восстановленных при одновременном измерении. Видно, что значения для образца в длинной ячейке восстановились лучше, чем для образца в короткой ячейке. Погрешности определения ε′ составили 5 и 5–10 % соответственно. Наибольший разброс значений наблюдается в области от 0,5 ГГц до 3 ГГц в областях интерференционных максимумов и минимумов, где как отмечено в [8] погрешность измерения существенно возрастает. На рис. 3 приведены частотные зависимости действительной части КДП ε′ для этих же образцов. Погрешности восстановления составляют 10–18 и 10–12 % соответственно.

Исследуемые образцы были также измерены по отдельности. Сравнение диэлектрических проницае-мостей показало, что значения для более сухого образца совпадают в пределах погрешности до 8,5 ГГц для действительной части КДП и до 4 ГГц для мнимой части КДП. Для более влажного образца удовлетворительное совпадение наблюдается до частоты 4 ГГц.

Многие программные пакеты компьютерной алгебры (например, Maple и Mathcad) и технических вычислений (например, Matlab) имеют встроенные средства оптимизации функций. Табличный процессор Excel не обладает гибкостью применения и широким функционалом как программы компьютерной алгебры, однако его несомненным достоинством является широкое распространение и низкая цена. Расширить возможности Excel, можно с помощью макросов, созданных во встроенной среде VBA, имеющей много общего с VBA.

Основным средством оптимизации в Excel является Solver, применяемый как в «ручном» режиме, так и в макросах VBA [9]. При увеличении числа переменных в оптимизируемой функции, полученный результат во многом зависит от начальных значений переменных. Используя VBA и Solver, была написана программа автоматического расчета диэлектрической проницаемости. Для проверки возможности определения диэлектрической проницаемости применение Solver осуществлялось в широком диапазоне начальных условий. Анализ восстановленных данных показал, что программа корректно восстанавливает значения КДП, если априорные значения отличаются от истинных не более чем на 10 %. Погрешность определения КДП при помещении ячейки в бокс не превышает 10 %, поэтому их можно выбирать как начальные.

Таким образом, показано, что метод восстановления КДП сразу двух образцов с использованием коэффициентов отражения и прохождения применим в диапазоне частот от 0,1 до 4 ГГц. Реализован алгоритм автоматического расчета КДП.