Коэффициенты переноса для трехкомпонентного деформируемого сплава

Описание процессов переноса в неравновесных условиях привлекает внимание многих исследователей, что связано в первую очередь с практическими приложениями. В неравновесных условиях поверхно- стной обработки материалов с использованием потоков частиц, обладающих высокой энергией (ионов, электронов), лазерного излучения, при осаждении покрытий из газовой фазы и плазмы, диффузия, связанная с иными видами переноса, зависит от эволюции всех переменных состояния. Даже если все протекающие в неравновесных условиях явления разной физической природы имеют разные характерные пространственные и временные масштабы, они оказывают влияние друг на друга, и это необходимо учитывать при математическом моделировании.

Известно, что диффузионные потоки элементов зависят не только от градиентов концентраций. Перенос массы может быть связан и с наличием в системе градиента температуры или градиента давления. Внешние поля (электрическое, магнитное, гравитационное) также оказывают влияние на механизм массопереноса. Выражения для диффузионных потоков с использованием аппарата термодинамики необратимых процессов выводились неоднократно как для газов и жидкостей, так и для твердых тел.

Тем не менее при исследовании частных задач возникают вопросы, которые связаны как с невозможностью найти все коэффициенты переноса в имеющейся в распоряжении справочной литературе, так и с невозможностью их непосредственного расчета из так называемых первых принципов, за которым не стояли бы достаточно жесткие ограничения. Излишняя поспешность в выводе формул часто приводит к «переопределенности» систем коэффициентов переноса: независимых среди них оказывается много больше, чем должно быть вследствие принципов симметрии в перекрестных явлениях [1]. Но даже принципа симметрии Кюри, который авторы [ 1 ] называют четвертым постулатом термодинамики необратимых процессов (ТНП), оказывается недостаточно для уменьшения числа коэффициентов, которые требуется определить из дополнительных предположений. В теории диффузии в сплавах для этой цели привлекают приближения «идеального», «неидеального», «регулярного» растворов; теорию Вагнера [2] (кстати, также обладающую внутренней симметрией) и т.д.

Покажем далее, что «симметрия» дифференциальных уравнений состояния, следующих из уравнения Гиббса (записанного в любой форме), также приводит к сокращению числа независимых коэффициентов. Последовательный вывод формул для диффузионных потоков позволяет продемонстрировать, что учитывать прямой эффект (ска- жем, термодиффузию) и «отбрасывать» как несущественную вещь эффект обратный (диффузионную теплопроводность) некорректно.

Переопределение потоков в ТНП

Производство энтропии, связанное с явлениями теплопроводности и диффузии, имеет вид as = — т

^V T

J т ■ _т + Х J к

T      к = 1

(

T V

gk

^^^^^^^в

\

к

T

F k

n

IJ к = 0, к=1

где J т — поток тепла, J к - диффузионные потоки компонентов, число которых n; gk - их химические потенциалы или парциальные хими ческие энергии (энергии Гиббса), Fк - составляющая вектора внешних массовых сил, действующих на компоненту с номером к. Обобщенная сила, сопряженная потоку тепла, есть

Х_т =

V т

T

Потоку массы соответствует обобщенная сила

Х к =

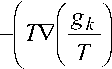
I

" F к

В соответствии со вторым законом термодинамики a s >  0.

Для удобства представления результатов и записи уравнений переноса потоки и «обобщенные термодинамические силы», входящие в (1), переопределяют [3, 4].

Так как

T V| gx I = т к т 7

^{( v} дк "Г_т

T

+ _! | °gk_ |vт - gk VT k тк отJ       т

)

к д т L

C

^{- s}x »

(ддк ^v т ткдт 7

^^^^^^^е

V т

8к т^т =

- Д [ S k T + 8 к ] V т = - hL V т , 22

то

° s = "  t

Jq ^T + E Jk ((Vgk ) T " F ) -

T      k = 1

где S k - парциальные энтропии, h k - парциальные энтальпии компонентов, C k - их массовые концентрации.

n

J q = J T " E h k J k                       (3)

k = 1

новое определение потока тепла. Очевидно, что такое переопределение не меняет ни производства энтропии (оставляя его инвариантным), ни потока энтропии.

Принимая гипотезу Онзагера о линейной связи потоков и сил, обеспечивающую неотрицательность производства энтропии, запишем

n

J q = L H X T + £ L qk X k ,                (4)

k = 1

^J k = L kq X q +

n

E ^Lj X j

j = 1

где

X q =" T^ ’ ^X k = ^{[ f} k "^{(v g} k ⁾ t 1 T•

В рамках расширенной термодинамики [5] и теории термоупругой диффузии [6] обобщением (4), (5) будут соотношения

n

J q = Lqq X T + E Lqk X ‘ + t k=1

dJ q q dt ’

n

^J k = L kq X q ⁺ E ^Lkj X j ⁺ t k j = 1

dJk dt ’

где t_q ,t k - времена релаксации к равновесному протеканию соответствующих процессов, k = 1,2,..., n . Наиболее распространенными являются теории с одним временем релаксации:

t k t q t r ‘

Феноменологические коэффициенты (коэффициенты Онзагера), обладающие свойством симметрии

Lkj = Ljk; Lqk = Lkq , могут быть определены на основе эксперимента или рассчитаны с использованием тех или иных гипотез о структуре вещества и характере взаимодействия частиц. Матрица коэффициентов является положительно определенной, что опять же есть следствие неотрицательности производства энтропии.

Так как не все потоки независимы, вместо (6), (7) найдем

J k = ^ L ki ( X i - X „ ) + L kq X q + t k J ,            (8)

i = 1

J q = Tq L qi ( X i - X n ) + L q, X q + t q J ■            (9)

i = 1

При описании неизотермической диффузии вводят в рассмотрение теплоты переноса Q так, чтобы они удовлетворяли системе уравнений n-1

L iq = ^L qi = ^, L ik Q k • k = 1

В силу свойств матрицы коэффициентов Онзагера эта система уравнений имеет единственное решение.

Определение коэффициентов переноса дадим для самых простых систем - бинарных и трехкомпонентных. Обобщение не представляет особого труда и может быть сделано аналогично.

Заметим, что в литературе имеются многочисленные описания явлений термодиффузии и диффузионной теплопроводности для условий p = const, а также явлений бародиффузии или диффузии под действием градиента напряжений в условиях T = const. Простое «суммирование явлений» приводит к потере слагаемых или к появлению «лишних» независимых коэффициентов.

Бинарная система

Пусть t q = t k = 0 и имеется два компонента. Тогда из (7), (8) найдем J 1 = L 11 ( X 1 ^- X 2 ^{) +} L 1 q X q , J q = L q 1 ( X 1 - X 2 ) + L qq X q .

Подставим в последние равенства выражения для термодинамических сил:

J 1 = T" ( F 1 - F 2 + ( V g 1 ) т - ( V g 2 ) т ) + L q | T ,

J q = T" ⁽ F 1 - F 2 +^{( V} g 1 ⁾ t -^{( V} g 2 ⁾ t ⁾+ L qq V T .

Энергия Гиббса g системы является функцией температуры, компонент тензора напряжений и состава. В этом случае [7, 8] можем записать

(V g 1 )t = -р-1а j Vaj + P11 V C + P^V C 2, (Vg 2 )T = -р 1a 2 Va ej +P12V C1 +P 22V C 2, где

R к     ⁵ g k

^P ' = C

V ^j 7 T , a i

il

= RTg kj m_kC_k ^,

P k = P k (как смешанные производные от непрерывной функции). Термодинамические множители g kj зависят от типа раствора, соединения и т.д.

_ C ⁵ In у j g" ^{jk +} C_t 5 In Ck ’

где у j - коэффициенты активности, m_k - молярные массы компонентов.

Следовательно, с учетом того, что V C 1 =-V C ₂, термодинамическая сила, вызывающая диффузию, будет иметь вид

X

D -

F 1 - F 2 + ° ij “ ij Va « - ( p l -p 2 — p 2 + p 2 ) v C 1 p

. T

Термодинамическая сила, сопряженная потоку тепла, не изменяется.

Для изотропной среды тензор коэффициентов концентрационного расширения имеет простой вид a ij - a k 8 ij •

Так как коэффициенты p k - симметричны, найдем g12

^g 21

m ₁ C ₁    m ₂ C ₂

или

C 1 ⁵ In Y 1 _ C 2 ⁵ In Y 2

.

C 2 5 In C 2    C 1 5 In C 1

Следовательно,

X

D ^-

F 1

^- F 2 ⁺

^a 1

^-a 2

P

e a ij

RT m ₁ C ₁

g 11

V

- ² g 12 + -CT g 22 V C m 2 ^C 2    )

_T ¹ . (13)

В частном случае идеального раствора (это приближение хорошо работает при малых значениях концентрации примеси, но часто с успехом используется и для неидеальных систем)

g 11 ^- g 22 ^- 1; g 12 ^- g 21 ^- 0.

В соответствии с теорией [3] феноменологический коэффициент Ln определяется через коэффициент самодиффузии (на основе сравнения с законом Фика):

L 11 ^-

P D 11 — A C 1

R

Аналогично вводим коэффициент теплопроводности (на основе сравнения с законом Фурье):

L qq

T 2 “^ т •

Тогда в приближении идеального раствора получаем следующие соотношения для потоков:

J i -

Р D 01 m i C l

RT

(

F 1

к

« 1 ^—a 2 _v —в

F 2 ^{+        va} kk

p

^^^^^^^s

RT

^f 1 + m 1 C L)

mC i к m 2 C 2 7

к v C + L

v T

1 q _{T 2} ^,

J, - — F q_T

^^^^^^^s

F ₂ + « 1

—I

к

p

« 2 V er e ^va kk

RT

^^^^^^^s

• ^f 1 + m l C L)

mC i к m 2 C 2 7

^v C i

• — X _T v T.

Коэффициент мый равенством

переноса под действием напряжений, определяе-

Bl - ЧА;1 («1 —a2 )’ RT производный от других параметров.

Коэффициент диффузии в приближении идеального раствора

D l - D l

i+mC к m 2 C 2 7

.

Коэффициент L_q обычно представляют так [4]:

> - Cidtp - где Dt - коэффициент термодиффузии. Иногда более удобным оказы вается введение коэффициента Соре (размерность коэффициента Соре есть К-1)

S

DT

T   _{D 1}

Следовательно,

L q i ^{- T} 2 C i d t ^{p - T} C l D l S T ^p •

В результате имеем

J i -—p D i V C i + B i C i Va kk

— C i D i S t pV T + ^p DRm¹ c ¹ ( F i — F 2 ) , (l7)

J q -—X T v T — D l Q * V C 1 + C 1 d i TS t [ ( « 1 —a 2 ) Va k _t +p ( F i — F 2 ) ] ,(18)

где Q * =

P 5I 1 s_t Г 1 + ^mC )

- теплота переноса (Дж/кг).

m l     I ^m 2 C 2 )

Если раствор - неидеальный, то внешне уравнения (17), (18) не изменяются, но появляется функция концентраций в коэффициентах:

D 1 = D 01 f ( C l ) ; 6 * =— $ т { ( C l ) , m *

f (C1) = g 11 - 2 g 12 +   Л1 L \ g 22 • m 2 (1 - C1)

Вид коэффициента B 1 не изменяется. Пользуясь разнообразными теориями, разработанными для сплавов, например [9,10], можем определить функцию f ( C ) с учетом достаточно тонких физических эффектов.

Интересно отметить, что в уравнении для потока тепла имеется слагаемое, которое формально можно трактовать как перенос тепла под действием градиента напряжений. Коэффициент переноса при градиенте напряжений является производной величиной - вычисляется через коэффициент Соре, коэффициент самодиффузии и коэффициент концентрационного расширения. Из шести коэффициентов переноса совершенно независимыми являются только три: коэффициент самодиффузии, коэффициент теплопроводности, коэффициент термодиффузии (или коэффициент Соре). Действие внешней силы связано с теми же коэффициентами.

Трехкомпонентная система

В этом случае имеем три уравнения для потоков:

J 1 = L 11 ⁽ X 1 ^- X 3 ^{) +} L 12 ⁽ X 2 ^- X 3 ^{) +} L 1 q X q ,

J 2 = L 21 ⁽ X 1 ^{- X} 3 ^{) +} L 22 ⁽ X 2 ^- X 3 ^{) +} L 1 q X q ,           ⁽¹⁹⁾

J q = L q 1 ( X - X 3 ) + L q 2 ( X , - X 3 ) + L qq X q .

Диагональные коэффициенты определим через коэффициенты самодиффузии:

т _ ^р D 11 ^m1^C1  _т _ ^р D 02 ^m 2 CC 2

.

^L         _ , L 77        _

• ¹¹ R ²² R

В теории диффузии часто принимают [8] | L 121 « L 11 , L 22 •

Это позволяет с учетом равенств

।v gk )t—-a kp1 v.-. ej+pk vC,+p kvC2+pk vCз -— -akp-lvae +(pk -p3)vC1 + (p2 -P3)vC2, к — 1,2,3

определить обобщенные силы X k и фузионных потоков в виде

представить уравнения для диф-

J 1 ^{— -p} D 11 ^v C 1 ^{- p} D 12 ^v C 2

+ ^p D ¹ " ¹ m¹ C ¹ [ F - F ] +

RT         ³

D 1⁰1 m 1 C 1 1

+ RT   (а ij

a 3 ) va ej - C j D u S t j pv T,

J 2 ^{— -p} D 21 ^v C 1 ^{- p} D 22 ^v C 2 ⁺

DmC^ [ F 2 - F 3 ] +

RT

+ D 22 m 2 C 2 ( „ 2

RT ij

^a J ^v ^ e ^- C 2 D 22 S T 2 ^{pv T} -

где введены коэффициенты Соре, связанные с коэффициентами термодиффузии соотношениями

^DT 1        ^DT 2

S —       , S 7 —       ,

T 1 _{D 11}     T 2 _{D 22}

и

D kj - D kk g kj

^^^^^^^в

g kn + V^ ( g nn

Cnmn

^^^^^^^в

g nj ^{) —} D kk f kj ^{- па}рц^иальны^е д^иф-

фузионные коэффициенты.

Аналогично предыдущему определим коэффициенты переноса массы под действием напряжений и феноменологические коэффициенты в уравнении для потока тепла:

^Dk ⁰ k^mk^Ck k

RT ij

^^^^^^^в

a n ) — D kk m k C k ( a k -a n ) — B k C k , RT

L q 1 - ^{T 2} C 1 D 11 S T 1 ^{p и} L q 2 “ ^T 2 C 2 D 22 S T 2 ^p •

Следовательно,

J i = -р D _nV C i -p D 12 V C 2 + B i CVa«„ -- C i Ai S t i PV T + C 1 DTm^{i P} ( F - F . ) ,

J 2 = -p D 21 V C i -p D 22 V C 2 + B 2 C 2 Va^ -

• - C 2 D 22 S t 2 PV T + CDm ^p ( F 2 - F . ) ,

J = -XV T - A V C - A V C ₂ + A Vo L + q T                   2    2 q kk

+ T p [ D i i cS t i ( F i - F 3 ) + D 22 C 2 S t 2 ( F 2 , - F 3 ) ] , где

Q k = P RT ² W»»^- ,

A i = D„ Q * + D ₂₁ Q 2 ,

A 2 = D i2 Q * + D 22 Q * ,

^Aq ^{= T [ D} ii ^C i S T i ( ^a i “ ^a 3 ^{) + D} 22 ^C 2 S T 2 ^{( a} 2 “ ^a 3 ^)] -

Из всего множества коэффициентов у нас независимы только четыре: D ,⁰, , D 22 , S_{t i5} S_t 2 , так как коэффициенты концентрационного расширения легко оцениваются на основе знаний о мольных или атомных объемах диффузантов. Более того, в связанных моделях эти же коэффициенты определяют величины напряжений в диффузионной зоне, связанные с неоднородным распределением концентраций.

В уравнении для потока тепла (22), как и в (I8), последнее слагаемое описывает перенос тепла при наличии градиента напряжений- Встречается ли такое явление в природе? Можно ли его «выделить» при экспериментальных исследованиях? Вопрос остается открытым. Соответствующий коэффициент переноса зависит от состава, теплот переноса и коэффициентов концентрационного расширения диффузантов.

Из (20)-(22) с учетом выражений для коэффициентов в них видно, что условие а, = A2 = 0 в общем случае возможно только тогда, когда теплоты переноса тождественно равны нулю. Это, в свою очередь, означает, что равны нулю коэффициенты Соре или коэффициенты термодиффузии. В соответствии с полученными формулами нельзя пренебрегать перекрестными эффектами по очереди: если есть прямой эффект, то обязательно есть и обратный эффект. Условие малости коэффициентов A1, A2 и Aq по сравнению с другими коэффициентами переноса не следует явно из каких-либо рассуждений и не может быть использовано вследствие их различной размерности.

Как правило, величина коэффициента Соре для электролитов, неэлектролитов и газов [4] 10 ^{- 2} - 10 ^{- 3} К^-1. Для полимеров этот коэффициент существенно выше. Для твердых тел данных найти не удается. Примем для сравнительной оценки всех коэффициентов переноса в системе Fe + C + N при малой концентрации примесей внедрения (C 1 = 0,03 -

-3 т,-1

углерод; C 2 = 0,03 - азот) 8_Т 1 = 8_Т 2 = 10 К . В этом случае можем воспользоваться приближением идеального раствора. В соответствии с данными [11, 12], при температуре 900 °С можно принять

D 0 = 3 , 6 - 10 ^{- 6}, D 0 ₂ = 2 , 3 - 10 ^{- 6} см²/с.

Молярные массы (г/моль) m ^ = 12 , 011 ; m 2 = 14 , 007 ; m 3 = 5 5 , 847 .

Следовательно, D 11 = 3,63 - 10 ^{- 6}, D₂₂ = 3,32 - 10 ^{- 6}, D ₁₂ = 2,47 - 10 ^{- 8}, D ₂₁ = 1 , 84 - 10 ^{- 8} см²/с; D_T 1 = 3 , 63 - 10 ^{- 9}, D_{T 2} = 3 , 32 - 10 ^{- 9} см²/(с<К).

Для оценки коэффициентов переноса под действием напряжений воспользуемся приближенными формулами для коэффициентов концентрационного расширения

• 1       ^to к

^а к -                 ,

• 3    to ^ + to 2 + to 2

где to к - атомные объемы. Учитывая величины атомных радиусов [12], находим а1 * 0,071; а2 * 0,073; а3 * 0,189.

Следовательно, B 1 =- 1 , 72 - 10 ^{- 11}, B 2 =- 1 , 26 - 10 ^{- 11} (см²-г)/(с^Дж).

Теперь можем определить оставшиеся величины:

Q 1 * 6433; Q * * 5424 Дж/см³;

A 1 * 0 , 0234; A ₂ * 0 , 0182 Дж/(см-с); A_q * 2 , 62 - 10 ^{- 4} см²/с.

Как и следовало ожидать, по абсолютной величине коэффициенты переноса, описывающие перекрестные эффекты, малы. Но в неоднородных системах с высокими локальными градиентами температу- ры, концентраций и напряжений возможны особенности, которые нужно исследовать с помощью специальных примеров. Перекрестные эффекты могут проявиться и в существенно неравновесных условиях обработки материалов высокоэнергетическими источниками, например в условиях электронно-лучевой обработки, ионной имплантации, лазерного воздействия, когда скорости роста температуры в поверхностном слое превышают сотни и даже тысячи градусов в секунду, что приводит к генерации механических возмущений и связанных с ними особых механизмов переноса.

Заключение

Таким образом, в работе осуществлен последовательный вывод уравнений для потоков тепла и массы для деформируемой среды. Показано, что в уравнении для потока тепла появляется дополнительное слагаемое, отвечающее за перенос тепла под действием градиента напряжений. Этот эффект отличен от того, который приводит к появлению эффекта связанности в уравнении теплопроводности, но вопрос о возможности экспериментального обнаружения эффекта остается открытым. В некоторых ситуациях, по-видимому, роль дополнительного слагаемого сводится к некоторой добавке к коэффициентам теплопроводности и теплотам переноса, подобно тому как иногда сводят роль диффузии под действием градиента напряжений к изменению диффузионных коэффициентов. Использование в качестве уравнений состояния дифференциальных соотношений, следующих из уравнения Гиббса при условии, что энергия Гиббса (или иной производящий термодинамический потенциал) - положительно определенная функция соответствующих переменных состояния, позволяет свести к минимуму число независимых коэффициентов. Так, в трехкомпонентной системе с учетом разнообразных перекрестных эффектов можно выделить как независимые величины коэффициенты самодиффузии, коэффициенты Соре и коэффициенты концентрационного расширения. Все остальные физические величины (теплоты переноса, парциальные коэффициенты диффузии, коэффициенты переноса под действием градиента напряжений и т.п.) легко рассчитать на основе представленных в работе формул. Это возможно, если приняты соглашения о структуре раствора (или сплава), позволяющие на основе известных теорий определять зависимости активностей или химических потенциалов компонентов от состава.

Результат легко обобщается на многокомпонентные системы, на системы с неравновесными вакансиями, на среды с иными реологическими свойствами.

Работа выполнена в рамках Государственного контракта № 16.740.11.0122, заключенного в рамках федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы по лоту «Проведение научных исследований научными группами под руководством докторов наук по следующим областям: математика; механика; информатика» (шифр «2010-1.2.1-102-017») по теме «Комплексное исследование взаимовлияния процессов переноса и деформирования в условиях воздействия потоков частиц на поверхность металлов» (шифр заявки «2010-1.2.1-102-017-075»).