Колебания консольно-защемленной толстой пластины
Автор: Папков С.О.
Статья в выпуске: 2, 2021 года.
Бесплатный доступ
В работе впервые представлено аналитическое решение задачи о свободных колебаниях консольно-защемленной толстой ортотропной пластины. Данная задача является достаточно громоздкой для использования точных методов теории упругости, в связи с чем для ее решения разрабатывались методы на основе вариационного подхода. В статье предлагается использовать метод суперпозиции для построения общего решения уравнений колебаний пластины в виде ряда по частным решениям, полученным на основе разделения переменных. При этом частные решения по одной из координат выбираются в форме тригонометрических функций специального вида (модифицированная тригонометрическая система). Построенное решение, в отличие известных в литературе решений на основе вариационного подхода, точно удовлетворяет уравнениям колебаний. Использование модифицированной тригонометрической системы функций позволяет получить единообразные выкладки для четных и нечетных форм колебаний и уменьшить число граничных условий на сторонах пластины с 12 до 9, при этом 5 из 9 граничных условий также выполняются точно. Структура представленного решения такова, что на границе пластины каждая из кинематических или силовых характеристик пластины представляется в виде суммы двух рядов - тригонометрического ряда и ряда по гиперболическим функциям. Относительно неопределенных коэффициентов рядов, представляющих решение, из оставшихся граничных условий, получена бесконечная система линейных алгебраических уравнений. Сходимость решения бесконечной системы по методу редукции исследуется численно. Приведены примеры численной реализации, на основе полученного решения выполнены численные исследования спектра собственных частот консольно-защемленной толстой пластины, как при вариации упругих характеристик материала, так и при вариации геометрических параметров.
Консольно-защемленная пластина, теория рейснера - миндлина, колебания, собственные частоты, собственные формы, аналитическое решение, бесконечная система линейных уравнений
Короткий адрес: https://sciup.org/146282041
IDR: 146282041 | УДК: 539.3 | DOI: 10.15593/perm.mech/2021.2.10
Текст научной статьи Колебания консольно-защемленной толстой пластины
ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2021PNRPU MECHANICS BULLETIN
Проблема колебаний консольно-защемленных пластин относится к одной из наиболее давних задач механики деформированного твердого тела. Элементы в форме консольно-защемленных по одному из краев прямоугольных пластин можно встретить во многих технических и строительных конструкциях, они являются неотъемлемыми элементами зданий, авиационного и автомобильного транспорта, различных приборов. По этой причине первые работы, посвященные проблеме колебаний подобных пластин, в рамках теории тонких пластин относятся к середине ХХ в. Young [1], используя произведения балочных функций в качестве базиса метода Релея – Ритца, одним из первых получил достаточно точные верхние оценки собственных частот колебаний изотропной квадратной консольно-защемленной пластины. В работах [2, 3] для решения той же проблемы было предложено использовать метод, основанный на вариационном принципе Рейснера. Заметим, что при этом подходе граничные условия на свободных сторонах пластины выполнялись не полностью, в частности условия на сдвиговые силы игнорировались. В работах [4–6] развиты модификации метода Релея – Ритца для анализа колебаний прямоугольных изотропных пластин в случае консольного защемления, которые позволили с достаточной точностью найти первые собственные частоты пластины и построить собственные формы колебаний. Можно заметить, что во всех упомянутых работах используются методы, основанные на вариационном подходе.
Однако, как известно, в ряде прикладных задач теория тонких пластин зачастую не позволяет адекватно описать структурный элемент, что привело к развитию теорий толстых пластин, в частности теории Рейснера – Миндлина [7]. Одно из первых теоретических и экспериментальных исследований колебаний толстых консольно-защемленных пластин представлено в [8]. В работе Lim и др. [9] был развит метод Ритца для анализа колебаний толстых изотропных пластин для ряда классических граничных условий, в том числе для консольного защемления. В качестве базиса метода Ритца авторами выбирается тригонометрическая система функций, обеспечивающая как выполнение граничных условий, так и достаточно быструю сходимость метода. Метод Ритца и его модификации остаются основой для теоретического анализа консольно-защемленных пластин и на сегодняшний день. Среди недавних работ можно отметить работы Liew и др. [10], где получены собственные частоты колебаний на основе pb-2 метода Релея – Ритца, в работе Cheung и Zhou [11] в качестве базиса метода Релея –Ритца предлагается взять статические балочные функции. Вариационный DSC – element method был предложен [12] для анализа свободных колебаний толстых пластин при различных граничных условиях. В работе [13] строится решение задачи о колебаниях консольно-защемленной пластины на основе вариационного подхода применительно к трехмерным уравнениям теории упругости.
На основе аналитических решений [14] в работах [15–17] развит Dynamic Stiffness method для колебаний изотропных толстых пластин. В статье [18] развит асимптотический подход к анализу высокочастотных колебаний прямоугольных пластин при различных граничных условиях. Для получения численного решения исследуемой задачи в [19, 20] используется метод конечных разностей, развитый с использованием теории степенных рядов. Численный подход на основе метода конечных разностей и метода конечных элементов также можно найти в работах [21-24]. В статье [25] авторы фактически используют метод суперпозиции для сведения задачи о колебаниях консольно-защемленной изотропной тонкой пластины к бесконечной системе линейных алгебраических уравнений.
В представленной статье на основе подхода [26-28] предлагается аналитическое решение задачи о колебаниях консольно-защемленной толстой ортотропной пластины. В отличие от предыдущих работ, посвященных колебаниям консольно-защемленной толстой пластины, построенное решение точно удовлетворяет разрешающим уравнениям колебаний. Выполнение граничных условий приводит к бесконечной системе алгебраических уравнений относительно неопределенных коэффициентов в общем решении.
1. Основные уравнения и структура общего решения задачи
где Q 4
k = —
2 D ’
phto 2
h 2
h
, Qh = — Q - частотные параметры;
A k = A”
4 D i ’
Упругие константы
V - A 55 i _ D 66 k _ D 66 + D 12
k^ , k^ , k
5 D i 6 D i D i
.
D i , D 2 , D 12 , D 66 , A 44 и A 55 сВяЗаны с
техническими константами (модулями Юнга Ex и E 2, модулями сдвига О12 и Ог3, О23, и коэффициентами Пуассона v12 и v2j) посредством соотношений
h3 E D _ h 3 E2 .
12(1 -V i2 v 21 ); 2 = 12(1 -v i2 V 21 ) ’
D 12 =
h 3 v i2 E 2 .
12(1 -v i2 v 2i ) ’
h 3 G
D 66 = "^y ; A 44 = K hG 13 ; A 55 = K hG 23 .
При этом граничные условия консольного защемления можно записать следующим образом:
x =
— a :
W = ф x = ф y = ° ,
x = a : M x = M xy = Q x = °,
y = ± b : M y = M xy = Q y = °,
Рассмотрим свободные колебания однородной толстой ортотропной пластины {( x , у ) е [ - a ; a ] х [— b ; b ]} постоянной толщины h . Согласно гипотезе теории толстых пластин Рейснера - Миндлина [7] элемент пластины смещается в прямолинейном направлении относительно срединной поверхности пластины, что приводит к следующему представлению компонентов вектора смещений:
где моменты и сдвиговые силы имеют вид
M x
D i
k °
дф°х (T , 5ф° My _ - dф X , yxy
--+ ( k — kG )----; ---- = ( k — kr )-- + k2---- a x 6 d y D a x 2 dy
дф.
;
M
xy
- = k 6
D i
dФX +дфУ l ay ax
;
U ( x, y,z,t ) = и 0 ( x, у, t ) + z ф ° ( x, y, t ), V ( x, у, z, t ) = v 0 ( x, y, t ) + z ф ° ( x, y, t ),
Qx , I dw ( y= = kJ —+ф
D 4 ( a x
>° ] . Qy. = k { d wL +ф ° x J’ D 5[a y фу
•
W ( x , у , z, t ) = w ° ( x , у, t )
Четное решение относительно оси у (индекс j =0) или же нечетное решение по у ( j =1) краевой задачи (2)-(3)
В случае гармонических колебаний углы поворота Ф ° ( x , у , t ) = ф x ( x , у )e‘ ю t , ф°, ( x , у , t ) = ф у ( x , у )e '™t и прогиб пластины w ° (x , у , t ) = W ( x , у )e1 ™ t должны удовлетворять уравнениям колебаний толстой ортотропной пластины:
|
I W ) |
1 |
I W k ] |
|
ф x [ ф у J |
= E k = 0 |
ф xx 1ф у» и |
d 2 ф x , a 2 ф x ,a'Ф y _ WW ] ^4 _n
"1+k + k6^X" + kX^T — k4 I + ф x l + Q h ф x = °, ox ay axoу [ax J
a 2 ф a 2 ф ~ a 2 ф I aw ]
k2 —y- + k6 —y- + k---- - k5 --- + ф + Q 4 фу = °, (2)
2 a у 2 6 a x 2 dxdy 5 [ a у y J h y
k 4
I a 2w aф]
I + -^x l
V a x 2 a x J
+ k
a 2W дф у aу2 dy
+q 4 w = °,
строится в форме суммы рядов с неопределенными коэффициентами Хы и Yln по модифицированной тригонометрической системе функций { T (a ^ x } и
{ T ( enjy ) } . Используя подход, представленный в статье [28], можно получить
W j = ^ k ° ( X 1,° k A 1,° kHj ( pl, °ky ) + X 2,° k A 2,° kHj ( p 2,° ky ) ) +
+ ^ j ° ( Y 1,° kE 1,° jHk ( q 1° j x ) + Y 2,° kE 2,° jHk ( q 2,° j x ) ) +
+ZZ Xi, *A, ^fl Pi, y T (a nkX) + n=1 l=1
+ ZZ Y , nk E i , n H k ( q l , n- x j n y ); n = 1 l = 1
Ф x , kj = 0 j 0 ( Y 1,0 k H k ( q 1,0 j X ) + Y 2,0 k H k ( q 2,0 j X ) ) +
+ ZZ X , nk B i , nk H j ( Pl , nky № nk X ) + n = 1 l = 1
+ ZZ Y , .H ( 4 l , nj X j n y ) n = 1 l = 1
Ф y , kj = 0 k 0 ( X 1,0 k H j ( p 1,0 k y ) + X 2,0 k H j ( p 2,0 k y ) ) +
+ ZZ X l , nk H j ( Pl , nky )Tk ( a nk X ) + n = 1 l = 1
+ ZZ Y , nk G l . nj H k ( q, , nj X )Т’(в „У ), (5)
n = 1 l = 1
где Tk ( z ) = (1 - k ) cos z + k sin z ; Hk ( z ) = (1 - k ) cosh z +
, . , я r, nf k )
+ k sinh z ; о mn - символ Кронекера; ank = — I n — I;
a I 2 /
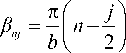
Величины q , p ( n =1, 2, …) являются корнями ветви l следующих характеристических бикубических уравнений:
cop 6 + cp 4 + c2p 2 + c3 = 0, (6)
doq 6 + dq 4 + d2q 2 + d3 = 0, (7)
d2 = в4 ( k5 ( k 2 + k 6 2 - k 2) + k2k4k 6) +
+ в2 (2k4k5 (k6 + k) - n4 (k^ + k62 - k2) --n: ( k2 k4 + k5 + k4 k6 + k5 k6)) + +n4 (n: (1+k6)-k5 - k4 k6)+k4 n: (n: - k5), d3 = -в6 k2k5k6 + в4 (-k2k4k5 + k2k6 n4 + ks n4 (k2 + k6)) +
+ p2 (n 4 ( kk + k5k 6 - k 2n 4 ) +
+n 4 ( k 4 ks - k 6 n 4 - k 5n 4 ) ) +n 4 ( n : - k 4 )( n : - k 5 ) .
Для случая n = 0 уравнения (6), (7) вырождаются [28] в биквадратные уравнения вида k2k5P04+(k2n4+k5n:) P02+n4 (n: - k5 )=0, (8)
k 4 q 0 + ( n 4 + k 4 n ; ) q 0 +n 4 ( n : - k 4 ) = 0. (9)
Заметим, что все представленные характеристические уравнения (6)–(9) допускают точное решение.
При этом значения величин A , E , B и G , l,nk , l,nj , l,nk l,nj , входящих в решение (5), могут быть выражены следующим образом для каждой ветви l характеристических уравнений:
kk 5 p l , nk k 4 ( k 2 p l , nk k 6 a nk k 5 +n : )
Pl, nk ( kk5 Pl, nk - kk4 ank + k4 k5 + k n4 ) , k5 Pl, nk + ( k2 Pl, nk - k6 a nk - k5 + n к ) ( k5 Pl, nk - k4 a nk + n ) ankPl,nk (kk5Pink - kk4“nk + k4k5 + kn4 )
где c0 = k2 k5 k6 ,
C 1 = a 2 ( k 5 ( k 2 - k 62 ) - k 2 ( k 5 + k 4 k 6 ) ) +
+ n4k5 (k2 + k6) + n4k2k6 - k2k4k5, c2 = a4 (k^ (k2 + k62 - k2) + k5k6) +
+ a 2 ( n 4 ( k2 - k 6 2 ) - k 5 П 4 ( 1 + k 6) - k 2 ( n 4 + k 4 n 4 ) +
+ k 4 ( 2 k 5 ( k 6 + k ) - k 6 П Л ) ) +
+ n4 (n: (k2 + k6 ) - k2k4 ) + k5 (^ (П - k4 ) - k6n4 ) , c3 = -a6 k4k6 + a4 (- k4k5 + k6 n4 + k4 n4 (1 + k6)) +
+ a 2 ( n 4 ( k 5 + k 4 k 6 - n : ) +
+n : ( k 4 k 5 - k 6 n 4 - k 4 n : ) ) +n 4 ( n : - k 4 )( n : - k 5 ) ;
d 0 = k 4 k 6
d1 = в2 (k4 (k2 - k62 - k2) - k5 k6) + n4 k4 (1 + k6) + n4 k6 - k4 k5, kk4 ql2 nj - k5 ( ql2 nj - k6 Pnj - k4 + n 4 ) ql, nj (kk4 qL - kk5 Pn+ k4 k5+ k n4),
G l , nj =
k 2 ql, nj + ( q l 2 nj - k 6 Pn j - k 4 +n 4 )( k 4 qk nj - k 5 P nj +n 4 ) q l,nj p nj ( kk 4 q^ nj - kk 5 P nj + k 4 k 5 + k n 4 )
k 5 pl ,0 k k 4 ql ,0 j
Al ,0 k z 2 , ^4 ; E l ,0 j 7 2 , ^4 .
k 5 Pl ,0 k + ^ k 4 q l ,0 j + ^
2. Сведение к бесконечной системе линейных алгебраических уравнений
Прежде всего, можно заметить, что с учетом четности решения по переменной y , из 12 граничных условий (3) достаточно выполнить девять (граничные значения кинематических и силовых характеристик для сторон y = b и y = - b совпадают с точностью до знака). Далее, из данных 9 условий 5 условий можно выполнить тождественно, так как в этом случае на границе пластины соответствующая характеристика пластины представляются полными тригонометрическими рядами с неопределенными коэффициентами. Например, из условия фх ( - a , y ) = 0 и формул (5) получаем
Ф х ,0, j ( - a , y ) + Ф x ,1, j ( - a, y ) =
= -^ j 0 ( Y ,00 H 0 ( q 1,0 j a )+ Y 2,00 H 0 ( q 2,0 j a ) ) +
+ 5 j 0 ( Y y)1 H 1 ( q 1,0 j a ) + Y 2,0l H 1 ( q 2,0 j a ) ) -
- ZZ Y , n 0 H 0 ( q , nj a ) T -(p nj y ) + n = 1 l = 1
да 3
+ ZZ Y , n 1 H 1 ' ( q . , n a ) ^ -( P n y ) = °- n = 1 I = 1
Отсюда, очевидно, следуют соотношения между неизвестными коэффициентами Y
- Y ,00 H 0 ( q j ) - Y 2,00 H j ( q ; a ) + Y , 0 1 H ( q^ j a ) + Y^ H ( q 2,0 j a ) = 0,
3 3 (10)
- Z Yi n 0 H 0 ( V ) + Z Y .n 1 H 1( V ) = 0. I = 1 I = 1
Кроме упомянутого граничного условия, аналогичным образом можно выполнить также условия M = Qx = 0 при x = a , если положить
( q 1,0 j E 1,0j - 1 )( Y 1,00 H 0 ( q 1,0 j a ) + Y 1,01 H 1 ( q 1,0 j a ) ) +
+ ( q 2,0 j E 2,0 j - 1 )( Y 2,00 H k ( q 2,0 j a ) + Y 2,01 H 1 ( q 2,0 j a ) ) = 0,
Z ( q , , nj G l , ny +P n )( Y , n 0 H j( q , nj a ) + Y , „ 1 H ( q , , .a ) ) = 0, (11)
l = 1
Z ( q- , nj E l , nj -1 )( Y , n 0 H 0 ( 4 t , nj a ) + Y , n 1 H ( q, , ^ a ) ) = 0. l = 1
Аналогично, на сторонах пластины y = ± b можно точно выполнить условия M = Q = 0 , если для неизвестных X выполняются следующие соотношения:
X 1,00 ( p 1,00 A 1,00 - 1 ) H j ( p 1,00 b ) +
+ X 2,00 ( p 2,00 A 2,00 - 1 ) H j ( p 2,00 Ь ) = 0,
Z X l , nk ( P l , nk B l , nk +a nk ) H j( P l , nk b ) = 0, (12)
l = 1
Z X l , nk ( P l , nk A l , nk -1 ) H ' ( P l , nk b ) = 0. l = 1
Уравнения (10)–(12) позволяют явно выразить неизвестные коэффициенты у,,n 1 через коэффициенты у,,n0, а неизвестные X2,nk, X3,nk - через X1,nk.
Действительно, введем для удобства новые неизвестные у,,nk = Y,nkHk (ql,nja) и xl,nk = X1,nkHj(Pl,nkb) , (13)
S nk
' 1
P 1, nk A 1, nk - 1
v P 1, nk B 1, nk + a nk
1 1 "
P 2, nk A 2, nk - 1 P 3, nk A 3, nk - 1
P 2, nk B 2,nk + a nk P 3nnk B 3,nk + a nk j
тогда из (10) и (11) получаем следующие соотношения:
2T 3
2T 1l , n
У1 , n 1 =7TT Z У / , n 0 - у , , n 0 , det T n i = 1
S
'l , nk = X 1, nk ( l = 2,3),
^ 11, nk
где T и S – алгебраические дополнения к элементам с индексами (1, l ) соответственно матриц T и S .
Аналогичные соотношения можно найти и для случая n = 0:
y 1,01 y 2,01
= T
* 0
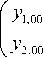
X 2,00 = 5 0 X 1,00 ,
где
q 1,0 j E 1,0 j q 2,0 j E 2,0 j
q 1,0 j E 1,0 j q 2,0 j E 2,0 j + 2
2 q 1,0 j E 1,0 j - 2
2 q 2,0 j E 2,0 j + 2 q 1,0 j E 1,0 j + q 2,0 j E 2,0 j
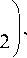
s 0
P 1,00 A 1,00 1
P 2,00 A 2,00 - 1
Таким образом, для решения поставленной задачи остается выполнить 4 граничных условия на сторонах пластины, используя неопределенные коэффициенты y ( l =1, 2, 3) и x ( k = 0, 1). При этом структура
представленного решения такова, что на границе пластины каждая из кинематических или силовых характеристик пластины представляется в виде суммы двух рядов – тригонометрического ряда и ряда по гиперболическим функциям. Используя схожесть разложения [29] на отрезке t e [ -т ; т ] гиперболических функций
п n t cosh qt по тригонометрическим функциям cos--- т
и sinh qt по системе функций sin
п (2 n - 1) t 2 т
согласно
а также матрицы, соответствующие левым частям систем (11), (12):
H k ( qt ) = 5 ^ 0 +2 q ^ H k ( qt ) т ч т m=*\
( - 1) m + kTk ( nf m - k ) t) т V 2 J
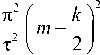
1 1 1
T n = q 1, nj E 1, nj - 1
q 2, nj E 2, nj 1 q 3, nj E 3, nj 1
a Q +B
^ q 1, nj 1, nj Vnj
q 2, nj G 2,nj +P nj q 3, nj G 3,nj +P nj J
получаем из краевых условий (3) бесконечную систему линейных алгебраических уравнений относительно неизвестных коэффициентов решения следующего вида:
5 ; о
A 1,00
+ s p 1,00
A 2,00 p 2,00 j
x 1,00
+ b ( E 10 j Coth 0 ( q i,0 j a ) -
2 k -5 j 0
22 q 1,0 j y 1,00 + q 2,0 j y 2,00
v q 20 j +a m 0 q 22,0 j +a m 0,
+
T 11,0 E 1,0 j COth 1 ( q 1,0 j a ) T 21,0 E 2,0 j COth 1 ( q 2,0 j a ) ) y 1,00 +
+ Ь ( E 2,0 j C0th 0 ( q 2,0 j a )- T 120 E 1,0 j COth 1 ( q i,0 j a ) -
' Z ( k 2 P l , m 0 l = 1
да
- k '« m 0 B l , m 0 ) COth j ( P l , m 0 b ) S 1 l , m 0 X m 0 +
T 22,0 E 2,0 j Co th 1 ( q 2,0 j a ) ) y 2,00
1 да 3 J С A
+ ZZ x nk Z = 0, (16)
к = 0 n = 1 l = 1 p l , nk v
+ 2 Z ( - 1 ) n + j Z
q l , nj ( k * qt , nj - k 2 P nj G l , n )
a m 0 + q 1, nj
-У1 , n 0 = 0, (22)
^ j 0 ( k ( 1 + s 0 ) ^ 1,00 + b ( q 1,0 j Coth 0 ( q 1,0 j a ) +
+ q 1,0 j T 11,0 Coth 1 ( q 1,0 j a ) + q 2,0 j T 21,0 COth 1 ( q 2,0 j a ) ) y 1,00 +
+ b ( q 2,0 j Coth 0 ( q 2,0 j a ) + q 1,0 j T 12,0 Coth 1 ( q 1,0 j a ) +
+ q 2,0 j T 22,0 COth 1 ( q 2,0 j a ) ) y 2,00 +
2 k ‘3 j 0
Л" a2 T л2 T q1,0jT11,0 q2,0 jT21,0
2 2 + 2 2
V_ q 1,0 j +a m 1 q 2,0 j +a m 1
2 q 1,0 j T 12,0 22 q 1,0 j + a m 1
q 2,0 j T 22,0
22 q 2,0 j + a m 1
y 1,00 +
I y2,00 +
)
1 ” 3 ( В a A I
+ ZZ(-1)kXnkZ k* - S11,nk = 0, k=0 n=1 l=1 V pl, nk ) )
- a Z ( k 2 Pl , m 1 - k ‘a m 1 B l , m 1 ) COth j ( P l , m 1 b ) S 1l , m 1 X m 1 + l = 1
да 3
+2Z(-1) n+jZ n=1 l=1
" 2 л q i,n/ ( k * q , n- k 2 P nj G i,n )
det T V
2 2
« m 1 + q t, nj
t -
ak 2 ( P 1,00 COth j ( P 1,00 b ) + s 0 P 2,00 COth j ( P 2,00 b ) ) X X- V 1,00 + k ^ j 0 ( y 1,00 + y 2,00 ) +
q l , n, -( k * q l , n- k 2 P n G l , nj )' “ m 1 + q l , nj J
y l , n 0
= 0,
” 3 Г R G 3
+ Z ( - 1) n + j Z k - k 2 j* y. , n 0 = 0, n = 1 l = 1 V q l , nj )
. - Hj( z ) ( - 1) nx 1
где к = к - k 6 , COth j ( z ) = —'— , X nk = —5— Hj ( z ) S 11, nk
A 1,00 P 1,00 S 0 A 2,00 p 2,00 | OV у1 A , nk S 11 , nk
R2 + n2 + R 2 n2 X 1,0 0 + 2 ZZX nk Z R2+ n2
Vе mj + p 1,00 P mj + p 2,00 ) k = 0 n = 1 l = 1 P mj + pl , nk
+ b ( - 1) j Z ( E l , mj ( COth 0 ( q l , mj a ) + COth 1 ( q , mj a ) ) -
3. Численные результаты
I --УЕ- Coth. fq -a)T- y „= 0, (19) i,mj 1 i,mj 1i,m l,m0 , det Tn i=1 )
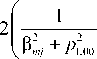
s 0
P mj + p 2,00
( - 1) m + j 3
x 1,00
1 да 3
2 ZZ X nk Z k = 0 n = 1 l = 1
S 1 l , nk
P mj + pl , nk
+ b— R---- Z ( G l , mj (C Oth0 ( 4 l , mj a ) + C Oth1 ( qi , mj a ) ) -
P mj l = 1
2 det T n
ZGi,mjCOth1 (qi,ma)Tu>m Iу.,m0 = 0,(20)
i=1
2 k *
2 p 1,00
VP mj + p 1,00
s 0 p 2,00
P mj + p 2,00
1,00
1 да , 3
2ZZ(-1)k Xnk Z k=0 n=1 l=1
pl , nk ( k pl , nk a nk B l , nk ) S 1 l , nk
p mj -+ P l 2 , nk
+
+ b (- 1 ) m+j Z ( ( q l , m - k * в mj G l . mj ) E l , m ( COth 0 ( q l , mj a )-
+ ^7 ^Z ( qi, mj- k *P mjG, mj) COth1 ( q, mja ) T1„ m jx x У., m 0 = 0, (21)
Для исследования и решения полученной бесконечной системы использовался пакет Mathematica. Согласно методу редукции полученная бесконечная система (16)–(23) сводилась к конечной системе относительно первых N неизвестных x^ и Ук„ о, при этом в расчетах удерживались первые (5 N + 3) уравнения системы в случае симметричных относительно оси Oy колебаний ( j = 0) и (5 N + 1) уравнений в случае антисимметричных колебаний ( j =1). Определитель конечной системы служил в качестве дисперсионного уравнения для определения собственных частот колебаний, а нетривиальное решение – для определения собственных форм колебаний. В табл. 1 представлена сходимость метода редукции при увеличении порядка аппроксимирующей системы.
В табл. 2 приведены первые собственные частоты квадратной изотропной пластины в сравнении с результатами [10] и [12]. Заметим, что в [10] используется модифицированный вариационный подход (DSC метод), в работе [12] классический метод – Релея – Ритца. Полученные результаты оказываются в хорошем соответствии с данными [10] и [12], что позволяет сделать вывод об адекватности предложенного подхода.
На основе полученного решения проводились численные исследования спектра собственных частот консольно-защемленной толстой пластины, как при вариации упругих характеристик материала, так и при вариации геометрических параметров.
Таблица 1
Сходимость метода редукции на первой собственной частоте Q: = 0.9301 для изотропной квадратной пластины при v = 0,3, к = 5/6, h / a = 0,1
Table 1
Convergence of reduction method for the first fundamental natural frequency Q: = 0.9301 of the isotropic square plate with v = 0.3, к = 5/6, h/a = 0.1
|
n |
1 |
2 |
3 |
5 |
|
y 1, n 0 при N = 10 |
-0,32742 |
0,195743 |
-0,152986 |
-0,114373 |
|
y 1, n 0 при N = 20 |
-0,351037 |
0,209318 |
-0,164008 |
-0,124418 |
|
y 1, n 0 при N = 40 |
-0,357335 |
0,212983 |
-0,167122 |
-0,127549 |
Таблица 2
_ A 4^2 -
Первые собственные частоты Q = —— изотропной п квадратной пластины при v = 0,3, к = 5/6, h/a = 0,1
Table 2
4Q2
First fundamental natural frequencies Q = —— п of the isotropic square plate with v = 0.3, к = 5/6, h / a = 0.1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Представленное решение |
0,3505 |
0,8170 |
2,0350 |
2,5839 |
2,8621 |
4,8172 |
5,4788 |
5,7741 |
|
[10] |
0,3735 |
0,8403 |
2,0502 |
2,5997 |
2,8752 |
4,8285 |
5,4885 |
5,7860 |
|
[12] |
0,3476 |
0,8168 |
2,0356 |
2,5836 |
2,8620 |
4,8162 |
5,4834 |
5,7769 |
В табл. 3 представлены первые десять собственных частот пластины из эпоксидного стекла при вариации ее толщины. Можно заметить, что при малой толщине пластины h / a = 0.01 собственные частоты колебаний в рамках теории Рейснера – Миндлина мало отличаются от соответствующих частот, вычисленных согласно теории тонких пластин. С увеличением толщины пластины различие между собственными значениями согласно теории толстых пластин и теории тонких пластин несколько увеличивается, но не превосходит 3 %.
Нетривиальное решение бесконечной системы (16)– (23) на собственной частоте колебаний позволяет построить согласно (5) собственные формы колебаний пластины. На рис. 1 представлены первые собственные формы колебаний квадратной консольно-защемленной пластины в случае ортотропного материала, представленного в табл. 3. Первая, третья и десятая формы колебаний соответствуют симметричным относительно оси Oy колебаниям (в приведенных формулах j = 0), вторая, пятая и седьмая формы колебаний – антисимметричным колебаниям (j = 1). Сверяя узловые линии построенных собственных форм с известными в литературе формами для тонких пластин [30], можно заметить, что отличия незначительны.
Таблица 3
Первые собственные частоты консольно-защемленной квадратной пластины при к = 0,8601 Вх = 60,7 ГПа,
Gn = G13 = G23 = 12 ГПa, v12 = 0,23,, v21 = 0,094
Table 3
First fundamental natural frequencies of the cantilevered square plate with к = 0.8601 E = 60.7 GPa ,
G 12 = G13 = G23 = 12 GPa , v12 = 0.23 , v21 = 0.094
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
h / a = 0,01 |
0,9363 |
1,3124 |
2,1443 |
2,3484 |
2,6147 |
3,2433 |
3,2674 |
3,9217 |
4,1035 |
4,4660 |
|
h / a = 0,05 |
0,9357 |
1,3080 |
2,1368 |
2,3417 |
2,6021 |
3,2202 |
3,2540 |
3,8955 |
4,0708 |
4,4362 |
|
h / a = 0,10 |
0,9346 |
1,2998 |
2,1212 |
2,3218 |
2,5725 |
3,1693 |
3,2197 |
3,8198 |
3,9877 |
4,3885 |
Заметим, что схожая ситуация наблюдается и для других граничных условий (например, полностью защемленной пластины и пластины со свободными краями [28]). Более того, соответствующие по номеру собственные формы в случае изотропного материала имеют тот же качественный характер, что и формы на рис. 1, количественные различия можно увидеть, например, на рис. 2, где представлены линии уровня первых двух собственных форм для ортотропного и изотропного материалов. Можно заметить, что в приведенном случае собственные формы колебаний почти совпадают.
Чтобы оценить, насколько ортотропные свойства материала влияют на спектр собственных значений консольно-защемленной пластины, рассмотрим пластину с защемлением по стороне y = — b из того же материала E = 60,7 FHa, G12 = G 13 = G23 = 12 Faa,[nW1] v12 = 0,23, v21 = 0,094, что и в предыдущих примерах. В этом случае материал уже оказывается более жестким в направлении, перпендикулярном защемленной стороне, что сказывается как на значениях собственных частот (табл. 4), так и на отвечающих им собственных формах колебаний (рис. 3[ПW2]).
Действительно, если первая частота колебаний в табл. 4 почти совпадает для обоих случаев защемления, то для второго типа защемления (по y = — b ) собственные частоты лежат существенно выше. Кроме этого, меняется и четность ряда форм колебаний; так, четвертая и пятая моды колебаний являются антисимметичной и симметричной, в то же время при защемлении пластины по стороне x = — a они соответственно симметричная и антисимметричная. На рис. 3 представлены вторая, третья, четвертая и пятая формы колебаний, соответствующих случаю защемления ортотропной пластины по стороне y = — b .
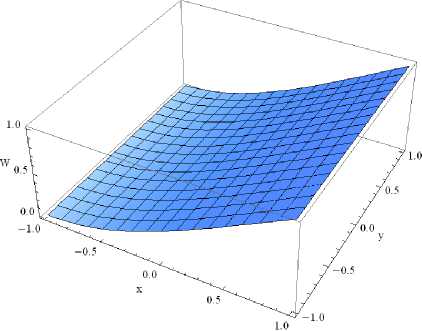
Ω 1 = 0.9346
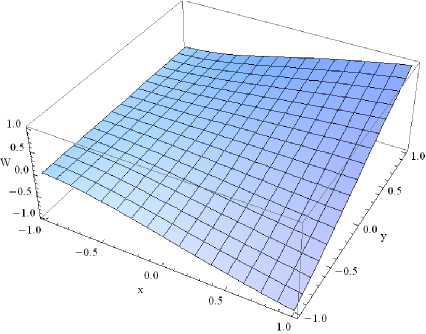
Ω 2 = 1.2998
б
а
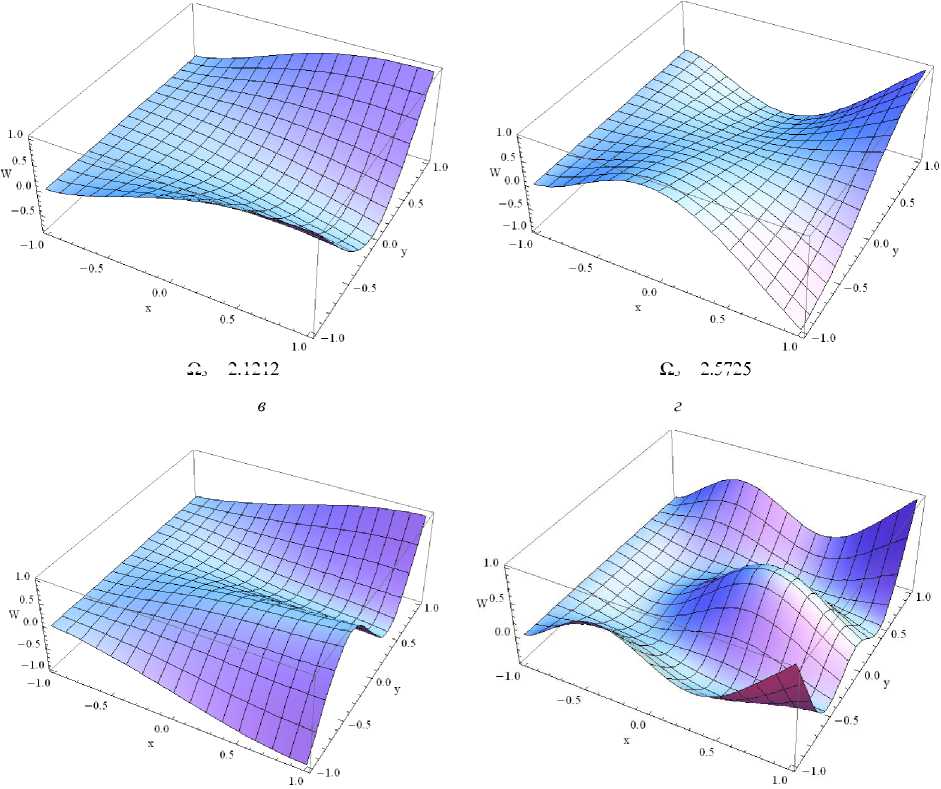
Ω 3 = 2.1212
Ω 5 = 2.5725
Ω 7 = 3.2197
Ω 10 = 4.3885
д
е
Рис. 1. Собственные формы колебаний консольно-защемленной толстой пластины: а , б , в , г , д , е – первая, вторая, третья, пятая, седьмая и десятая формы колебаний
Fig. 1. The natural modes of the cantilevered thick plate; (a), (b), (c), (d), (e), (f) are the first, second, third, fifth, seventh and tenth shape modes, respectively[ПW3]
1.0 -O’ 00 0..’ 1.0
а
б
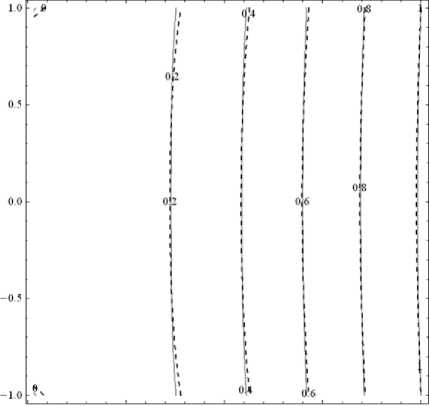
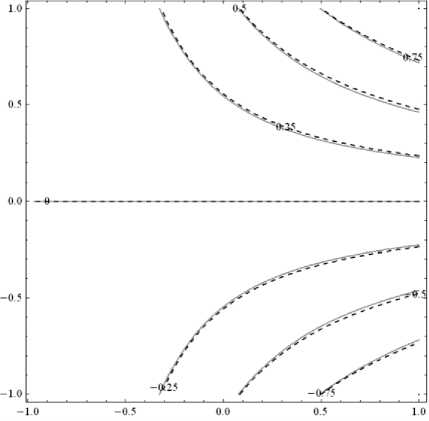
Рис. 2. Линии уровня собственных форм колебаний консольно-защемленной толстой пластины: а , б – первая и вторая формы колебаний (сплошная линия – ортотропный материал с данными из табл. 3, пунктирная линия – изотропный материал при ν = 0.3)
Fig. 2. Level lines of natural vibration modes of the cantilevered thick plate; (a), (b) are the first and second shape modes (the solid line shows the orthotropic material with data from Table 3, the dotted line shows the isotropic material at ν = 0.3)
Таблица 4
Первые собственные частоты консольно-защемленной толстой квадратной пластины
(Ex = 60,7 ГПа, Gn = G13 = G23 = 12 ГПа, v12 = 0,23, v21 = 0,094; h/a = 0,10) в случае защемления различных сторон пластины
First fundamental natural frequencies of the cantilevered thick square plate for the case of different clamped sides ( к = 0.8601 E = 60.7 GPa , G 12 = G13 = G23 = 12 GPa , v12 = 0.23, v21 = 0.094)
Table 4
|
1 |
2 |
3 |
4 |
5 |
|
|
f ♦ t__________ |
0.9346 |
1.2998 |
2.1212 |
2.3218 |
2.5725 |
|
0.9348 |
1.5301 |
2.3255 |
2.8626 |
3.0903 |
Таким образом, можно предположить, что при консольном защемлении пластины на спектр колебаний большее влияние оказывают упругие свойства материала в направлении, перпендикулярном защемленной стороне.
Заключение
Таким образом, в работе впервые на основе метода суперпозиции построено аналитическое решение задачи о свободных колебаниях консольно-защемленной ортотропной пластины. Данное решение, в отличие от вариационного подхода, точно удовлетворяет уравнениям колебаний, 5 из 9 граничных условий также выполнены точно. Оставшиеся граничные условия приводят к бесконечной системе линейных алгебраических уравнений, сходимость решения которой по методу редукции исследована численно. Решение, представленное в статье, имеет самостоятельное практическое значение, состоящее в том, что высокочастотные колебания консольно-защемленных пластин встречаются в различных прикладных задачах технического характера (микро- и наноэлектронике, в задачах строительной механики, при моделировании технических систем, в геофизике и др.), также данные решения могут быть использованы для параметрической оптимизации, для анализа устойчивости к вибрации технических систем.
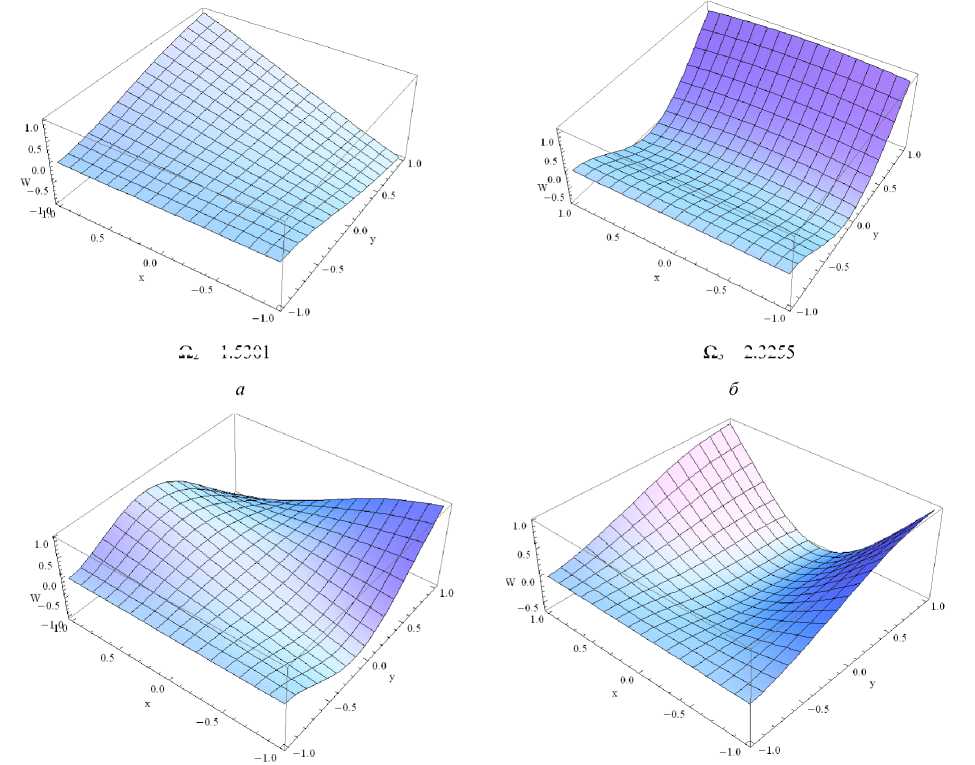
Ω 2 = 1.5301
Ω 3 = 2.3255
Ω 4 =2.8626
Ω 5 = 3.0903
в г
Рис. 3. Собственные формы колебаний консольно-защемленной толстой пластины: а , б , в , г – вторая, третья, четвертая и пятая
Fig. 3. The natural modes of the cantilevered thick plate; ( a ), ( b ), ( c ), ( d ) are the second, third, fourth, fifth shape modes
Исследование выполнено при финансовой поддержке РФФИ и города Севастополя в рамках научного проекта № 18-41-920001.
Список литературы Колебания консольно-защемленной толстой пластины
- Young D. Vibration of rectangular plates by the Ritz method // J. Appl. Mech. - 1950. Vol. 17, no 4. - P. 448-453.
- Plass H.J., Gaines J.H., Newsom C.D. Application of Reissner's variational principle to cantilever plate deflection and vibration problems // J. Appl. Mech. - 1962. - Vol. 29, no 1. -P. 127-135.
- Austin R.N., Caughfield D.A., Plass H.J. Application of Reissner's variational principle to the vibration analysis of square flat plates with various root support conditions // Developments in theoretical and applied mechanics. - N.Y.: Plenum press, 1963. -P. 1 -24.
- Barton M.V. Vibration of rectangular and skew cantilever plates // J. Appl. Mech. - 1951. - Vol. 18, no 1. - P. 129-134.
- Martin A.I. On the vibration of a cantilever plate // Quart. J. Appl. Math. - 1956. - Vol. 9. - P. 94-102.
- Claassen R.W., Thome C.J. Vibrations of a rectangular cantilever plate // J. Aerospace Sci. - 1962. - Vol. 29, no 11. -P. 1300-1305.
- Mindlin R. Influence of rotatory inertia and shear on fleuxural motion of isotropic elastic plates // ASME Journal Applied Mechanic. - 1951. - Vol. 18. - P. 31-38.
- Plunkett R. Natural frequencies of uniform and nonuniform rectangular cantilever plates // J. Mech. Eng. Sci. -1963. - Vol. 5, no 2. - P. 146-156.
- Lim C. W., Liew K.M., Kitipornchai S. Numerical aspects for free vibration of thick Part I: Formulation and verification plates // Comput. Methods Appl. Mech. Eng. - 1998. - Vol. 156. -P. 15-29.
- Liew K.M., Xiang Y., Kitipornchai S., Transverse vibration of thick rectangular plates - I. Comprehensive sets of boundary conditions //Computers& Structures - 1993. - Vol. 49(2). -P. 1-29.
- Chung J.H., Zhou D. Vibration of moderately thick rectangular plates in terms of a set of static Timoshenko beam functions // Computers& Structures. - 2000. - Vol. 78(6). -P. 757-768.
- Xiang Y., Lai S.K., Zhou L. DSC- element method for free vibration analysis of rectangular Mindlin plates // Int. J. of Mech. Science. - 2010. - Vol. 52. - P. 548-560.
- Seok J., Tiersten H.F., Scarton H.A. Free vibrations of rectangular cantilever plates. Part 1: out-of-plane motion // Journal of Sound and Vibration - 2004. - Vol. 271, no. 22. - P. 131-146.
- Gorman D. J. Free vibration analysis of Mindlin plates with uniform elastic edge support by the superposition method // Journal of Sound and Vibration. - 1997. - Vol. 207, no. 3. -P. 335-350.
- Kolarevic N., Nefovska-Danilovic M., Petronijevic M. Dynamic stiffness elements for free vibration analysis of rectangular Mindlin plate assemblies // Journal of Sound and Vibration. -2015. - Vol. 359 - P. 84-106.
- Shear deformable dynamic stiffness elements for a free vibration analysis of composite plate assemblies - Part I: Theory / M. Nefovska-Danilovic, N. Kolarevic, M. Marjanovic', M. Petronijevic // Composite Structures. - 2017. - Vol. 159. -P. 728-744.
- Free vibration study of sandwich plates using a family of novel shear deformable dynamic stiffness elements: limitations and comparison with the finite element solutions / M. Marjanovic, N. Kolarevic, M. Nefovska-Danilovic, M. Petronijevic // Thin-Walled Structures. - 2016. - Vol. 107. - P. 678-694.
- Иванова Е.А Асимптотический и численный анализ высокочастотных свободных колебаний прямоугольных пластин // МТТ. - 1998. - № 2. - C. 163-174.
- Usarov М. Dynamic Design of Thick Orthotropic Cantilever Plates with Consideration of Bimoments // World Journal of Mechanics. - 2016. - No. 6. - P. 341-356.
- On the Simple and Mixed First-Order Theories for Plates Resting on Elastic Foundations / A.M. Zenkour, M.N.M. Allam, M.O. Shaker, A.F. Radwan // Acta Mechanica - 2011. -Vol. 220. - P. 33-46.
- Torabi K., Afshari H. Vibration analysis of a cantile-vered trapezoidal moderately thick plate with variable thickness // Engineering Solid Mechanics. - 2017. - Vol. 5(1). - P. 71-92.
- Huang C.S., Leissa A.W., Chang M.J. Vibrations of skewed cantilevered triangular, trapezoidal and parallelogram Mindlin plates with considering corner stress singularities // International Journal for Numerical Methods in Engineering. - 2005. -Vol. 62. - P. 1789-1806.
- Free vibration analysis of plates using least-square-based on finite difference method / M. Huang, X.O. Ma, T. Sakiyama, M. Matuda, C. Morita // Journal of Sound and Vibration. - 2005. -Vol. 288. - P. 931-955.
- Nguyen-Xuan H., Liu G.R., Thai-Hoang C. An edge-based smoothed finite element method (ES-FEM) with stabilized discrete shear gap technique for analysis of Reissner-Minslin // Computer Methods in Applied Mechanics and Engineering. -2010. - Vol. 199. - P. 471-489.
- Sukhoterin M., Baryshnikov S., Aksenov D. Free Vibration Analysis of Rectangular Cantilever Plates Using the Hyperbolic-Trigonometric Series // American Journal of Applied Sciences. - 2016. - Vol. 13 (12). - P. 1442-1451.
- Papkov S.O. A new method for analytical solution of inplane free vibration of rectangular orthotropic plates based on the analysis of infinite systems // Journal of Sound and Vibration. -2016. - Vol. 369. - P. 228-245.
- Papkov S.O., Banerjee J.R. A new method for free vibration and bucking analysis of rectangular orthotropic plates // Journal of Sound and Vibration. - 2015. - Vol. 339. - P. 342-358.
- Papkov S.O. New analytical solutions for vibration problem of thick plates // PNRPU Mechanics Bulletin. - 2019. -№ 4. - P. 145-156.
- Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Элементарные функции. - М.: Наука. Глав. ред. физ.-мат. лит-ры, 1981. - 800 с.
- Leissa A.W. Vibration of Plates (NASA SP-160). -Washington, DC: Govement Printing office, 1969. - 353 p.


