Колебательное возбуждение молекул кислорода в активной среде кислородно-йодного лазера
Автор: Азязов В.Н., Пичугин С.Ю., Сафонов В.С., Уфимцев Н.И.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Лазерная техника и технология
Статья в выпуске: 1 т.4, 2002 года.
Бесплатный доступ
Проведен расчет заселённостей колебательных уровней кислорода в активной среде химического кислородно-йодного лазера. Показано, что имеет место существенно неравновесное заселение колебательных уровней кислорода. Относительная заселенность колебательных уровней кислорода в активной среде может достигать нескольких десятков процентов. Менее половины убывшей энергии от запасенной в синглетном кислороде идет на нагрев газовой смеси, остальная часть поступает на диссоциацию йода, в электронные и колебательные степени свободы компонентов среды. Электронно-возбужденные состояния йода I2 (А' и А) могут служить промежуточными состояниями в процессе диссоциации йода, которые заселяются при столкновениях с колебательно-возбужденными молекулами синглетного кислорода.
Короткий адрес: https://sciup.org/148197678
IDR: 148197678 | УДК: 621.373
Текст научной статьи Колебательное возбуждение молекул кислорода в активной среде кислородно-йодного лазера
Отличительной особенностью химического кислородно-йодного лазера (ХКЛ) является существенно неравновесное заселение электронных и колебательных состояний компонентов его активной среды. Более половины молекул кислорода находятся в электронно-возбужденном синглетном состоянии, а несколько десятков процентов в колебательно-возбужденном состоянии [1, 2]. Активная среда лазера формируется в результате протекания нескольких десятков реакций, компонентами которых, как правило, являются возбужденные частицы. Хорошо известно, что колебательная энергия может увеличивать скорость передачи электронной энергии [3]. В работах [1, 2] предложен механизм диссоциации молекулярного йода в среде синглетного кислорода (СК). Активную роль в диссоциации играют электронно-возбужденные состояния йода I2(A ‘ ) и 1 2 (A) и колебательно возбужденные молекулы СК. В настоящей работе I2(X), I2(A ‘ ), I2(A) обозначают молекулы йода в электронных состояниях X1 ^ , A ‘ 3 n 2 u и A3 n iu соответственно; O2(X), O2(a), O2(b) - молекулы кислорода в электронных состояниях X: E , а1 А и b1 ^ ; I, I * - атомы йода в состояниях 2P3/2, 2P1/2.
Колебательное возбуждение молекул в среде ХКЛ может быть важным не только в процессе диссоциации молекул йода, но и в процессах дезактивации электронной энергии. В реакциях пуллинга (1) и (2) (табл.) происходит убыль СК на вышестоящий электронно-возбужденный уровень O2(b), который эффективно тушится на парах воды по реакции (5). В работах [4-6] найдены температурные зависимости констант скоростей этих реакций. В [4] измерена константа скорости реакции (1) в интервале температур 300 + 1850 К. Измеренная константа очень быстро растет с температурой. Реакция пуллинга (2) - это один из основных процессов тушения синглетного кислорода. Температурная зависимость данной реакции была измерена в диапазоне T=259 - 353 К [5]. Было найдено, что отношение К2/К1 постоянно в этом температурном диапазоне. Можно предположить, что это отношение постоянно и при более высоких температурах.
Результаты эксперимента [4] указывают на то, что возрастание энергии в поступательных степенях свободы сталкивающихся партнеров увеличивает константу скорости реакций пуллинга. Энергия колебательных степеней свободы молекул среды может также увеличивать константы скоростей этих реакций. Влияние колебательной энергии молекул на скорость реакции может быть существенным. Это наиболее просто описывается моделью Парка [7]. В этой модели вместо температуры T в выражение для констан-
Таблица. Список реакций
Таким образом, процессы с участием колебательно-возбужденных молекул O2(a, v) могут быть определяющими в ходе тушения синглетного кислорода и приводить к заметному снижению лазерной эффективности. Поэтому представляет несомненный интерес определение заселенностей колебательных уровней O2(a, v) в среде ХКЛ. Настоящая работа посвящена теоретическому исследованию распределения молекул кислорода по колебательным уровням в лазерной среде и его влияния на коэффициент усиления ХКЛ.
Расчётная модель
Мы предполагаем, что газовый поток на входе в лазерный реактор состоит из молекулярного кислорода в электронных состояниях XX, a ' A bX с концентрациями NX, Na, Nb, паров воды с концентрацией N w и молекулярного йода в основном электронном состоянии I2(X,X) с концентрацией NI2. Рассмотрим поток с постоянным поперечным сечением с дозвуковой скоростью (при числе Маха M 2 = U 2 /а 2 << 1 ) в предположении мгновенного смешения газовых потоков (U и a - скорости газа и звука соответственно).
Молекулярный йод быстро диссоциирует в присутствии синглетного кислорода. Процесс диссоциации не достаточно ясен. К настоящему времени предложено несколько каналов диссоциации I 2 [1, 15, 23, 24]. Каждый канал может вносить свой вклад в процесс диссоциации. Основная проблема - это определение доминирующего канала среди них.
В настоящей работе мы используем механизм диссоциации, в котором электронновозбужденные промежуточные состояния I2(A ‘ ) или I2(A) заселяются при столкновениях с колебательно-возбужденными молекулами O2(a, v=1 или 2) (реакции (10) и (11)) [1,2]. Последующие столкновения с O2(a) вызывают диссоциацию I2 (процесс (12)). Значения констант скоростей K10 и Кн не известны. В [15] наблюдалось, что O2 гораздо эффективней тушит I2(A ‘ ), чем Ar и H 2 O, поэтому в [15] сделан вывод, что это тушение обусловлено в основном ЕЕ процессом (22), разрешенным принципом Франка-Кондона, а также тушение I2(A ‘ ) на O2 обусловлено доминированием обратной реакции (10). Реакция (10) не удовлетворяет принципу Франка-Кондона. Однако, известны быстрые реакции EE-обмена, запрещенные этим принципом. Если предположить, что константа скорости обратной реакции (10) равна константе скорости тушения I2(A ‘ ) на O 2 -Кщ =6,3 х 10-12 см3/с, измеренной в [15], то из принципа детального равновесия мы можем оценить верхний предел константы скорости прямой реакции (10), то есть K + = 2 х 10-12 см3/с.
Заметим, что энергии возбуждения состояний O2(a, v=2) и I2(A) почти одинаковы: 10823 и 10847 cm-1 соответственно. Можно предположить, что резонансный EE обмен энергий между этими состояниями происходит в ходе процесса (11). Константа скорости этой реакции не измерена, поэтому мы проводили расчеты для трех значений этой константы: K1I1 =0, KI =2х10-11 и K™ =2х10-10 см3/с. В настоящей работе мы предполагаем, что I2(A) тушится компонентами среды ХКЛ, так же как и I2(A‘). Реакции (1, 2, 4-7, 9, 13, 14) -это реакции релоксации. Колебательные уровни кислорода заселяются по реакциям пуллинга (1, 2), (4) и при тушении O2(b) парами воды (реакция (5)). В реакции (1) образуются в основном колебательно- возбужденные молекулы O2(b, v=2) [26]. О колебательном возбуждении продуктов реакции (2), (4) и (5) известно мало. Вероятность колебательного возбуждения H2O(001) в реакции (5) равна 0,1 [27]. Возможно, основная часть высвобождающейся энергии в реакциях (2), (4) и (5) идет на возбуждение колебательных уровней кислорода [28]. Обмен колебательными квантами между молекулами синглетного кислорода происходит в процессах (15), а между молекулами кислорода в различных электронных состояниях - в процессах (16) и (17).
Изменение долей компонентов
П j = g j / g ox , газовой температуры T и коэффициента усиления g в среде ХКЛ вдоль координаты Х описываются следующими уравнениями:
dna „(Nox X Г To ]2 х dx U 0 ( T J х (-2Kin 2 - K 2П an I * - K А an I +
+ K 3 - n X n I * + K 5 П ь П w - ^ о П а 1 П 1 2 +
+ К1 о П X n A - К п П a 2 П 1 2 + К и П X n A -
+ Кп П а ( Л A ' + n A )) ;
d n b ( N ox ) 0 Г T o )'
= 1 х dx U 0 ( T J х (Kin a2 + K 2n an I * - K 5n ьП w -
- k 8 n ь П i 2 - k 9 n ь П i 2 ) ;
d n I * ( N ox ) o ( T o )2
= 1 х dx U 0 ( T J х (-K 2П an I * + K л an I - K 3-n X ПI * -- K 4П xni *- K бП 12П i *- K 7П wni *);
|
d n A ' _ ( N ox ) о ( T O 1 1 X dx U 0 ( T J Х ( ^ Л a 1 n 1 2 - K -n X n A ' - - К 12 П a n A ' - Кв П а П w - K -. n а П N 2 ) ; |
n i n i — ( n + l) + 1 ’ 1 — °’1’2’3’- _ B - B B 2 - 4 ( C 1 - 1 ) C 1 nan1 . „., n a 1 " 2( C 1 - 1) • (24) |
|
d n A _ ( N ox ) 0 ( T O 1v — 1 X dx U 0 ( T J X ( Кп П а 2 n 1 2 - Кп П X n A - - К 12 П a n A - Кв П A n w - К 14 П A n N 2 ) ; |
n — C2n 2 n a 0 . a 2 n 0 + n a 0 ( C 2 - 1)’ C 1 — exp ( 104/ T ), C 2 — exp ( 213/ T ); |
|
d n 1 2 ( N ) о ( T o 12 — 1 X dx U 0 ( T J X ( - K 8 n ь П 1 2 - К 12 П a ( n A- + n A )) ; |
C 3 — exp ( 324/ T ), B — n a ( C 1 - 1 )+ C 1 n 1 + n 0 ; n a 0 = n a - n a 1 ; n x + n a + n ь — 1; |
|
dn v — ( N ox ) 0 f T o. 1 2 X dx U 0 ( T J X № / 2,1 + 7V)K 1 n a 2 + (2 / 2,2 + / 1,2 ) K 2 n a n I * + +(3 y 3,4 + 2 / 2,4 + 7 1, 4 )K 4 Л x n i * + + (3 Y 3,5 + 2 7 2,5 + y 5 )K 5 Л ь П w -
|
n io — n i + n i * — 2{( n 1 2 ) 0 - n 1 2 } ; 7 a( N .x ) 0 T 0 g — 24 Tl(3 n i * n io ); T U — FU 0 ; T 0 к 3 -— k 3 + / K eq ; |
|
d n . 1 ( N ) 0 f T 1 2 dx U 0 ( T , X { в 1,7 K 7 n w n I * + £ 1,5 K 5 n ь П w + + K 20 П v n w - K 20 П w 1 ex P ( A E / kT ) - - K 21 П w n w + K 21 П w ex p ( - E w / kT )} ; |
K eq — 0,75exp(402/ T ); ( т 0.5 0 — 1,3 X 10 - 17 1-0- cm 2 ; I T J ( N ox ) 0 — 9,66 X 10 P ( T°° ) cm - 3 ; - 0( K ) |
|
dT : ( N o, ) 0 f T> 1 2 X dx C p (1 + h)U 0 ( T , X ( q 1 К 1 П a + q 2 K 2 П а П i * + q 4 K 4 П x n i * + + q 5 K 5 n ь П w + q s K 6 n 1 2 n i * + q 7 K 7 n w n i * + + q g K 9 n ь П 1 2 + q 13 K 13 n w ( n A + n a ) + q 14 K 14 n n 2 ( n A ' + n a ) + q 18 K 18 n v n w + + q 19 K 19 n v + q 21 K 21 n w 1 n w ) ; |
K. — 9,5 X 10 - 28 T 3- 8 exp ( 700 /Te )^ 1 eJJ eJJ K — 4 X 10 - 24 T 3, 8 exp ( 700/T, „,) ; 2 eJJ eJJ rp rp s rp 1 - s T eJJ — T T v ; T — • v k ln ( 1 + 1/ n v ) Индексы a, b, X обозначают электронные состояния кислорода a1 A , b1 ^ и X3 L , соответ- |
ственно; I*, I - атомы йода в электронны х состояниях 2P1/2 и 2P3/2; А ’ и A - молекулярный йод в электронных состояниях А’3 П 2и и А3 П 1и соответственно; I2 - молекулярный йод во всех состояниях; w - пары воды; 0 обозначает начальное состояние; gox = NoxU - суммарный поток кислорода; g . - поток j-той компоненты; q . - энергия, выделяющаяся в j-ой реакции; C p - молярная теплоемкость газовой среды; п . - доля кислорода на i- том колебательном уровне; п w1- доля молекул H2O(010); П v - средний запас колебательных квантов в молекулах кислорода; Y i. - вероятности возбуждения i-го колебательного уровня О2 в j-ом процессе; в 1. - среднее количество колебательных квантов в изгибной моде молекул воды, которое возбуждается в j-том процессе; K e q - константа равновесия реакции (3); о - сечение индуцированного излучения для перехода I(2P1/2, F = 3) ^ I(2P3/2 = 4) при T=T 0 ; E 2 и E 1 - колебательные энергии H2O(010) и O2(a, v = 1) молекул; h - степень разбавления буферным газом; P - давление газа.
Уравнение (23) описывает изменение среднего запаса колебательных квантов О2 вдоль координаты X. Если скорость возбуждения колебательных уровней молекул кислорода намного меньше, чем скорость V -обмена в процессах (15)-(17), то распределение молекул О2 по колебательным уровням будет Больтцмановским (формулы (24)) [29].
Результаты расчетов и их обсуждение
Для среды состава O2(X):O2(a):H 2 O:I2:N2 = k:l:m:n:s имеем следующие начальные значения долей компонентов:
(П a ) 0 = ТГ1 ; П1 2 ) 0 = 777 ;
k + l k + l
(n I * ) o = ( n A ' ) o = ( n A ) o = 0;
П w
ms
1+7; n N 2 = k+7'
Начальное значение среднего запаса колебательных квантов O 2 принимаем равным доле молекул кислорода на первом колебательном уровне на выходе генератора синглетного кислорода [2]:
( П v ) 0 = ( П 1 ) о = ( 2 / 2,1 + 7 1,1 ) -K^ +
К 20 П w
+ ( 2 Y 2,1 + 7 ц + Д,5 ) f ^ y X
K 21 n w
( А Е ) (
X exp l — + exp l -
I kT J A
] . kT J
Аналогично для начального значения доли колебательно-возбужденных молекул воды имеем [2]:
(П w 1 ) о = ( 2 / 2,1 + / 1,1 + 3 1,5 ) 4K1 n a- + ex P К 21 n w
( w
I kT J
Начальное значение доли молекул O2(b) можно с высокой точностью найти из равенства скоростей их образования в процессе (1) и убыёи в реакцин (5): ( n ь ) о = К 1 П 2 / ( К 5 П w ) ■
Мы рассчитывали средний запас колебательных квантов молекул O 2 , доли синглетного кислорода, атомарного и молекулярного йода, коэффициент усиления и температуру в зависимости от координаты х для среды состава O2(X):O2(a):H2O:I2:N2=300:700:20:10:0 при следующих параметрах: U 0 =100 м/с; T0=300 ° K; P0=1 Тор; Cp=29,085 Дж/моль; y , 1 =i; Y 11 =i; y , 2 =i; y 2 =°; y „ =1; Y 4 =0; Y 4 =0; y„=0,8; Y 2,5 =0; Y 1,5 =0; ■ P 1,5 =°.2; P 1,7 =3; q^q-’Y q4=37717 Дж/моль; q5=16216 Дж/моль; q6=90996 Дж/моль; q7=33731 Дж/моль; q9=37490 Дж/моль; q13=q14= 119570 Дж/моль; q18=q19= 17763 Дж/моль; q21=19092 Дж/моль.
На рис.1 представлена расчетная зависимость доли O2( 1 А ) от координаты х для трех значений параметра модели Парка: s=1; 0,5; 0,2. Значение s=1 соответствует случаю, когда колебательное возбуждение молекул кислорода не влияет на скорость реакций пул-линга. Видно, что потери электронной энергии быстро увеличиваются с расстоянием при s < 0,5. Для примера, при x=10 см и s=0,2 расчетная доля синглетного кислорода составляет 39 %, а при s=1 она равна 61%. Таким образом, колебательное возбуждение молекул 0 2 может существенно увеличить скорость потерь электронной энергии в ХКЛ.
На рис.2, 3 представлены расчетные зависимости коэффициента усиления от коор-
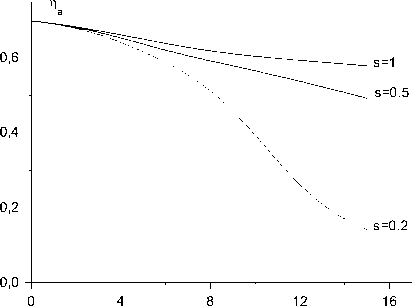
Рис.1. Расчетная зависимость доли синглетного кислорода от координаты х для трех значений параметра модели Парка s=1; 0,5; 0,2 при
K™ = 2 х 10"10 см3/с динаты х. Максимальное значение коэффициента усиления и соответствующее ему значение координаты xmax изменяются незначительно при изменении s и K11. Быстрые потери электронной энергии при s<0,5 приводят к резкому падению коэффициента усиления активной среды в потоке после xmax. Процесс (11) при K ™ < 2 х10 "11 см3/с не оказывает влияние на скорость диссоциации йода (рис.3). На рис.4 представлена расчетная зависимость среднего запаса колебательных квантов O2 от х при трех значениях параметра модели Парка: s=1; 0,5; 0,2. Учет влияния колебательной энергии на скорость реакций пуллинга (1) и (2) увеличивает скорость заселения колебательных уровней O2. Энергия
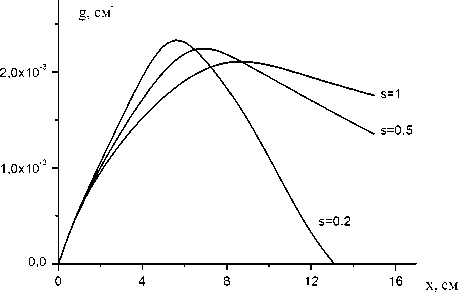
Рис.2. Расчетный коэффициент усиления ХКЛ g в зависимости от координаты х при трех значениях параметра модели Парка: s=1; 0,5; 0,2 и K™ = 2 х 10 "10 см3/с
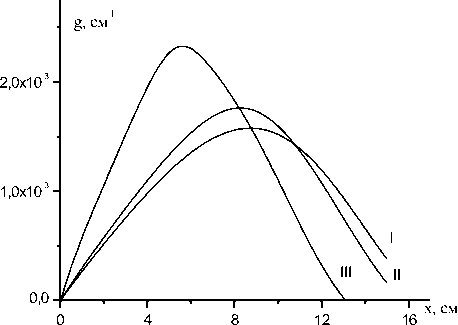
Рис.3. Коэффициент усиления g ХКЛ в зависимости от координаты х, рассчитанный при s= 0,2 для трех значений константы скорости K11: кривая I - K11 = 0 см3/с; кривая II-K" = 2х 10"11 см3/с; кривая III -KЦ = 2х 10"10 см3/с синглетного кислорода при его релаксации идет на возбуждение поступательных, колебательных и электронных степеней свободы атомов и молекул среды.
Доли энергии, идущие на возбуждение различных степеней свободы, определяются следующими формулами:
£ T = C p ( T - T 0 ) / A Q a - доля, идущая на термический нагрев, £ v = E 1 n v / A Q a - доля, идущая на колебательное возбуждение молекул кислорода, £ b = E b n b / A Q a - доля электронной энергии, приходящаяся на состояние O2(b), где
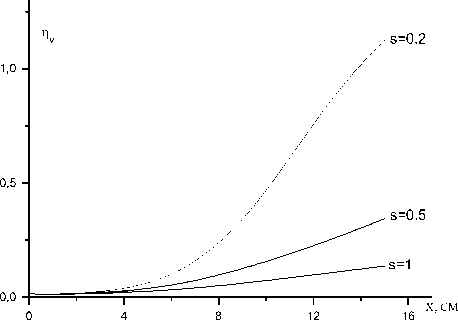
Рис.4. Расчетные зависимости среднего запаса колебательных квантов молекул кислорода от х при K™ = 2 х 10 "10 см3/с для трех значений параметра модели Парка: s=1; 0,5; 0,2
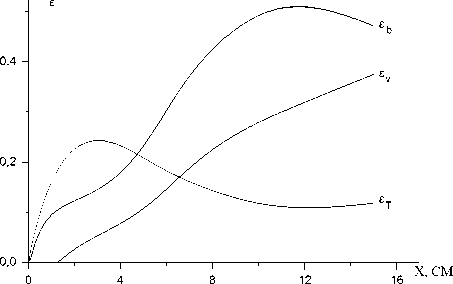
Рис.5. Доли электронной энергии синглетного кислорода, идущие на поступательные ет, колебательные ev и электронные еь степени свободы, в зависимости от координаты x при s=0,2 и K 1 III = 2 х 10 - 10 см3/с
A Q a = E a [ ( П a ) o - n a ] - потери электронной энергии, запасенной в синглетном кислороде, Ea, E b - энергии электронно возбужденных состояний O2(a) и O2(b) соответственно. Рис.5 показывает, что большая часть энергии синглетного кислорода идет в электронную и колебательную энергию. Например, при x = 10 см £ b=0,49, £ v=0,28 и только 11 % идет на поступательные степени свободы.


