Колебательные процессы в камере горения доменных воздухонагревателей

В теплонапряженных камерах горения доменных воздухонагревателей возможно возникновение и развитие динамических процессов различного амплитудно-частотного диапазона, что сказывается на надежности и эффективности работы всей системы подготовки доменного дутья. Условия возбуждения колебаний в камере горения, соединенной с подкупольным объемом, определяется соотношением инерционных, упругих и диссипативных свойств среды в элементах системы горения топлива, а также наличием существенных акустических импедансов в отдельных участках тракта. Поддержание колебаний обеспечивается существованием обратной связи, действие которой подчиняется условию Рэлея: фазовое соотношение между пульсациями давления и колебательной составляющей тепловыделения должно подчиняться зависимости:

^h-bpdx>0, (1) т где h - интенсивность тепловыделения при горении, В т/м3; Зр - колеблющаяся компонента давления, Па; dx - время, с; Г - длительность цикла, с.

Условие Рэлея, не совсем точно называемое критерием Рэлея [1], дает удовлетворительное объяснение механизма перехода тепловой энергии в механическую при пульсирующем горении с точки зрения термодинамики. Но использование этого условия в качестве критерия устойчивости системы, как показал Б.В. Раушенбах [2], неправомерно: система горения в процессе развития колебательного процесса реализует такие амплитудно-фазовые соотношения и такой механизм обратной связи, которые обеспечивают в заданных условиях максимум акустической энергии, излучаемой областью горения. Самопроизвольное движение системы горения топлива к максимуму потерь акустической энергии отвечает поведению системы при увеличении энтропии.

При большой величине акустической емкости подкупольного объема Са_к =V_K( ре² и большой относительной длине С_{к г} = /_{к г} /d_{K г} камеры горения, в последней устанавливается, при соблюдении условия Рэлея, режим пульсирующего горения. Как показано в монографии Б.В. Раушенбаха [2], в этом случае в камере горения теплоподводом возбуждаются устойчивые колебания давления Ьр , Па, и объемной скорости Зи, м³/с, которые можно описать системой дифференциальных уравнений:

об   бо ф

— + М — + — = 0;

5т      с5с 5х

= 0, бт мот имеющей решения й = [ЛФ1(^) + ^<Р2 (^

P = VA>4>3A^xV^Ap4>iV^x)\^e , (5) где комплексная частота р = v + /ю определяется в соответствии с акустическими свойствами камеры горения со =0,5лс/7_кг.

В формулах (2)-(5): Ay, Ар - коэффициенты краевых условий, определяемые при х = 0, т = 0 ; х = х//к г - безразмерная продольная координата; х=хс(1кт - безразмерное время; М = и]с число Маха; и = Зи/с - безразмерная вариация объ- емной скорости и, м3/с; р = 8р/ ж = ср jcv — показа тель адиабаты.

Функции

Ф1 (х) = 0,5

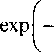
рх

М + \ J

+ ехр

Рх

М-\

;(б)

Ф2(х) = 0,5

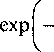
Вх ।      (

--- -ехр -

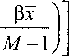
отражают изменение амплитуды колебаний вдоль координаты х .

Решения (4) и (5) дают возможность определить качественную картину стоячих волн давления и скорости в камере горения воздухонагревателя высотой Z_{K г} при условии Са_к —> оо и со =0,5лс//_кг (рис. 1). Из рис. 1 можно определить, что пучность давления 8р и узел скорости би расположены у закрытого конца камеры горения, а узел давления 5р и пучность скорости би -у ее открытого конца. Расположение горелочного штуцера вблизи пучности давления, то есть у закрытого конца камеры горения, обеспечивает энергетический источник автоколебаний при пульсирующем горении.

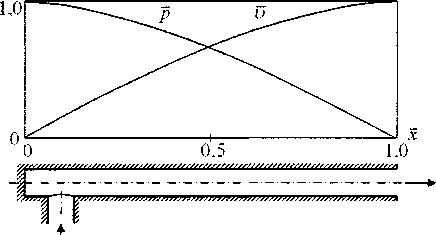
Рис. 1. Эпюра вариаций давления р и скорости V [2]

Модель Б.В. Раушенбаха весьма точно отражает действительный ход процесса при Са_к —> со и о = О,5лс/7_кг ; в основу ее положено представление о камере горения как об элементе с распределенными параметрами: массовые и упругие свойства потока газов распределены по длине камеры горения.

Если представить камеру горения, составленной из сосредоточенной акустической емкости у закрытого конца и массы газов в горловине, то можно получить уравнение для возмущений давления 8р, связанных с изменением объемного расхода продуктов сгорания 6G = s'8p, отвечающее модели В.Б. Штейнберга [3]:

-^-Bp + ^k-s^— 6p + [®Q -ks\<5p = 0 . (8) dv dx ^v '

В уравнении (8) величина к отвечает коэффициенту потерь на трение в горловине при колебани ях, который можно назвать «динамическим коэффициентом трения». Величину 5 = s'^pjo можно определить как «коэффициент отрицательного трения», так как 5 через s' = 8и/8р связывает прямой пропорциональной зависимостью возмущения давления 8р с возмущениями объемной скорости би. Физического аналога «отрицательному трению» в природе нет, поэтому следует признать, что под видом параметра s в модель В.Б. Штейнберга введен механизм обратной связи, подчиняющийся условию Рэлея. Модели В .Б. Штейнберга отвечает камера сгорания сосредоточенного объема V с выходной горловиной длиной / и площадью поперечного сечения F. Привести камеру горения доменного воздухонагревателя, где обычно I/d = 10-12, к модели В.Б. Штейнберга весьма трудно, однако анализ этой модели весьма полезен с точки зрения изучения природы пульсирующего горения.

Устойчивость системы по уравнению (8) определяется по соотношению величин к и s: при к> s колебания в системе затухают, при к < s -растут, значению к = s соответствует граница устойчивости. Зависимости подобного рода определяются для камер сгорания газотурбинных установок и напорных парогенераторов. Попытку применить подобные зависимости для камеры сгорания доменного воздухонагревателя нельзя признать удачной, так как в работе [4] и акустическая масса Ма , и акустическая емкость С а определены по полной длине камеры горения /_{к г}, таким образом, полная длина камеры горения входит и в упругий, и в массовый элемент, что лишено физического смысла.

При малых значениях параметров s -» 0 , к —> 0 потеря устойчивости проявляется в виде колебательного процесса с частотой ю₀, которая приближается к собственной частоте резонатора Гельмгольца. Рассчитанные при этих условиях собственные частоты /₀=т₀ /2л изображены на рис. 2, где половина длины камеры горения отнесена к сосредоточенному объему, вторая половина -к сосредоточенной массе. На графике нанесена точка А , соответствующая камере горения высотой 33 м и гидравлическим диаметром d = 3,2м (Г = 8,1м²) при температуре 1200 °C. Расчетная частота для этих условий /₀ ^ 7,65 Гп, фактические частоты при пульсирующем горении /= 3,3-3,5 Гц [5]. Расчетные условия для кривых на рис. 2: 1-Z= 1500 °C, Z = 2Z=23 м; 2 - ф= 1300 °C, £ = 28м; 3 - ф_р =1100 °C, Г=36м; 4 -ф_р = 900 °C, L = 40 м; 5 - ф_р = 700 °C, L = 44 м. На рис. 2, кривая 6, также нанесены значения собственных частот для бесшахтных воздухонагревателей Калугина ВНК при температуре в зоне горения ф_р = 1500 °C.

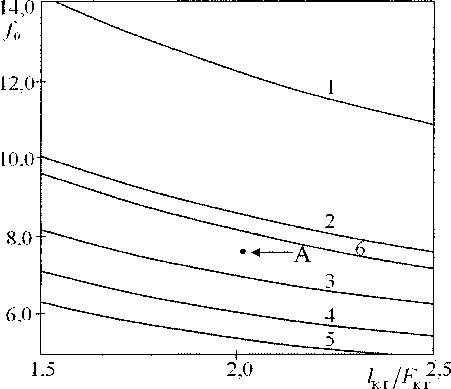
Рис. 2. Собственная частота /₀ (Гц) камеры горения с размерами /_кг и F_Kr в приближении ее резонатором Гельмгольца (1-6 в тексте)

При уменьшении акустической емкости подкупольного объема Сак упругие силы, вызываемые сжатием газов в объеме Гк, влияют на дина мические процессы в камере горения; эти процессы могут быть описаны однородным уравнением второго порядка в вариациях d2 NT 2Л GBX —^-8р + —2— + —1-^-dT2 [СакР Мак.г .

:б]

d , — бр + di

2k_xk_YG_BX 1

Met, _тСа_Кй Ма_{К г}Са„ . Л.1 Л*              К.1 к. .

5р = 0.

Здесь MaKY = plKT/F, кг/м4 - сосредоточенная акустическая масса потока газа в камере горения длиной /кг ис площадью поперечного сечения FKT; Car=VK/pc2, м^сЧкг - сосредоточенная акустическая емкость объема Гк при скорости звука с, м/с, в этом объеме; ^ - коэффициент потерь давления в камере горения; р - крутизна напорной характеристики камеры горения в рабочей точке. Величина F связывает объемный расход газовой среды на входе в камеру горения GBX с расходом на выходе GBMX kY=Gsx/GBMX в рав новесном режиме.

Частота колебаний в этом случае определяется по формуле г                            л0,5

1 2кхкG ю= --------+---1 т вх =

_      К.1      К           К.1 КI _ передаточная функция колебательного звена - камеры горения в области изображений по Лапласу будет иметь вид

s

Д

(И)

Коэффициент затухания колебаний 8 определяется по формуле

8 =

kT kxGBX

2CaKP MaK r

Перенос возмущений звеньями «к.г» (камера горения) и «к» (подкупольный объем) в этом случае можно описать зависимостями:

Здесь переносные свойства звеньев отражены их передаточными функциями W_XY (s) ; W^ (s);

W_XY (s) ; W_x (s), определяемыми по зависимостям, подобным (11).

В уравнении (10) принято, что камера горения обладает сосредоточенной акустической массой Ма_кт без учета ее упругих свойств, что справедливо при небольшой длине 1_КТ. С увеличением /_кг становится существенной сжимаемость газа, это приводит к появлению стоячей волны в камере горения с узлом давления у выхода в подкупольный объем и пучностью в начале камеры горения. Учет влияния сжимаемости газа в камере горения в этом случае можно произвести введением в Ма_{к г} приведенной длины /_пр = 0,5/_{к г} ив Са_к приведенного объема Г_пр = Г_к + 0,5/_кгГ_кг.

Граница устойчивости системы, состоящей только из звеньев «к.г» и «к» может быть определена при 8 = 0 из (12); так как все величины в правой части (12) существенно положительны, за исключением р, то при р > 0 система безусловно устойчива. При р < 0 граница устойчивости опре деляется равенством ^т _ kxGBX

2Сакр ~ Мзкт

таким образом, полное условие устойчивости имеет вид

₽>

kYMaK г 2kxCaxGBX

При уменьшении Сак -> 0 возрастает акустический импеданс выходного конца камеры горения до величины, соответствующей «акустически закрытому» концу.

На рис. 3 приведены кривые зависимости частоты Д собственных колебаний в камере горения от ее длины /кг при различных условиях возбуждения. Чисто акустическому возбуждению, когда

/₀ =0,25с//_кг, соответствуют кривые 5, 6, 7 при разной средней температуре в камере горения F = 1100-1500 °C.

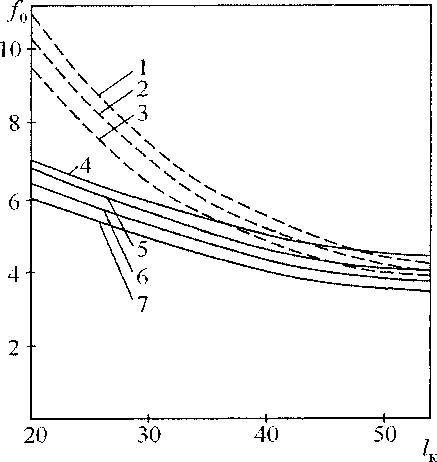
Рис. 3. Собственные частоты fQ (Гц) камеры горения длиной /кг при различных условиях возбуждения

(1-7 в тексте)

Кривая 4 рассчитана для условий возбуждения камеры горения совместно с подкупольным пространством как системы с сосредоточенными параметрами по формуле (9). Как показали расчеты, частота собственных колебаний в этом случае для камеры горения длиной /_кг = 35м составляет /₀ = 5,3 Гц и на 12 % выше соответствующей частоты для чисто акустического возбуждения. В расчетах принято: к, = 100; к_Т = 0;2; G_BX =10⁵ м³/ч.

Эксперименты с установкой датчиков пульсаций давлений в поднасадочном пространстве и в подкупольном объеме показали, что возбуждение часто распространяется на массу газов, находящихся в насадке. Величина акустической массы Ман = 1,2, то есть соизмерима с MaKt, и «подключение» Ман к колебаниям существенно сни жает частоту примерно в отношении 1/72 =0,708. При этом частота колебаний для случая кривой 4 рис. 3 снизится с 5,3 до 3,75 Гц.

Представлению о камере горения как о системе, имеющей акустические емкость и массу, определяемые по приведенным значениям Гпр и /пр, отвечают кривые 1, 2, 3 рис. 3. Здесь приведенные величины определяются по формулам:

у _ у ₊ О^т ^кт .

пр                          ,

—+1

I F

ЧТ¹ V Г

0,5 + —

/ F

• 7        7    __________ К.Г

^;пр ~ ^к.г         у *

1+—

I F

К.Г К.Г

На рис. 4 представлены результаты расчетов собственной частоты при возбуждении камеры горения с подкупольным объемом при повышении тепловой нагрузки, что соответствует увеличению GBX . Снижение /0 при увеличении GBX приводит к тому, что при повышенных тепловых нагрузках частота колебаний согласно (9) становится равной частоте акустических колебаний. Этим частично объясняется тот факт, что режим пульсирующего горения наступает при повышенных тепловых нагрузках.

Выводы

• 1.    Проведенный анализ возможных механизмов возникновения колебательных процессов в системе горения топлива доменных воздухонагревателей позволил определить частотный спектр

  

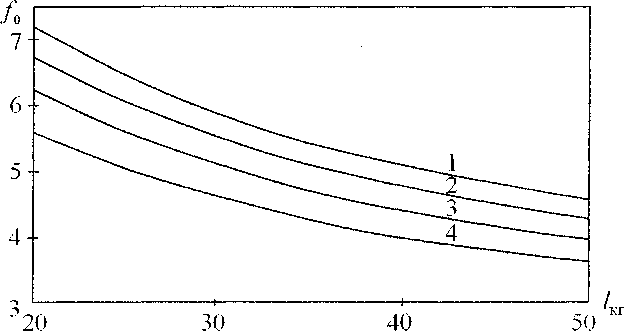
  Рис. 4. Собственные частоты /₀ (Гц) при возбуждении камеры горения длиной /_кг (м) совместно с подкупольным объемом: 1 - G_BX = 0,7-10⁵ м³/ч;

  2 - G = 0,8-10⁵ м³/ч; 3 - G = 0,9-Ю⁵ м³/ч; 4 - G = 10^s м³/ч

  
  

• 2.    Реализация конкретного механизма зависит от сигнала обратной связи по каналам подачи компонентов горения и движения продуктов сгорания; для развития и поддержания колебаний требуется выполнение условия Релея.

• 3.    Фактически наблюдаемый спектр частот при пульсирующем горении топлива в доменных воздухонагревателях является результатом взаимодействия сигнала обратной связи с рассмотренными в работе механизмами возникновения колебательных процессов.

собственных колебаний при различных конструктивных и режимных параметрах.