Количественная оценка потерь информации и характер построения очередей в пакетных сетях

Традиционные методы преобразования сетевого трафика направлены на то, чтобы обеспечить гарантии достаточной пропускной способности для достижения ожидаемого качества обслуживания. Степень, с которой это возможно в реальных условиях функционирования мульти-сервисной сети, до конца не выяснена. Это связано с самоподобностью трафика и обусловленных этим трудностей моделирования процессов в сетевых структурах.

Очевиден тот факт, что изначально не проявляющие свойства самоподобия потоки данных, пройдя обработку на узловых серверах и активных сетевых элементах, начинают проявлять ярко выраженные признаки самокорреляции [1].

Это оказывает влияние, прежде всего, на производительность сети и на качество обслуживания, которое существенно зависит от двух факторов: модели обслуживания, которая определяет различные классы пользователей и устанавливает распределение сетевых ресурсов и процедур определения свойств трафика, необходимых для распределения этих ресурсов, и эффективности их использования.

Мультисервисные сети, имеющие дело с самоподобными трафиковыми объединениями (например, пакетами), передаваемыми из одной сети в другую, не в состоянии предоставить гарантии требуемого качества, за исключением тех случаев, когда трафик имеет определенную форму в четко заданной области. Модель обслуживания в этом случае основывается на промежуточном объекте, называемом потоком, который представляет собой последовательность пакетов определенного приложения.

Путем распределения ресурсов на потоковом уровне обеспечение качества обслуживания разделяется на две части:

• 1.    Механизмы обслуживания, гарантирующие удовлетворительное качество услуг.

• 2.    Механизмы управления, обеспечивающие высокую эффективность использования сетевых ресурсов.

В этом случае удобно различать три характеристики качества обслуживания: прозрачность, доступность и предоставляемая пропускная способность. Чтобы соответствовать требованиям прозрачности, сеть должна реализовывать определенную модель обслуживания. Требования доступности обеспечиваются заданием объема сетевых ресурсов с учетом случайной структуры пользовательского спроса. Предоставляемая пропускная способность, прежде всего, определяется тем, как модель обслуживания распределяет эти ресурсы между различными потоками, и определяется как скорость передачи, доступная пользователю данной службы.

Состояние вопроса

Ключевым понятием в описании широкополосных сетей связи является скорость передачи службы, определяемая в рекомендациях ITU-T, как скорость передачи, доступная пользователю данной службы. Эта скорость представляет собой стохастический процесс x ( t ) и имеет вероятностное описание [2].

Из физических соображений всегда существует ограничение максимальной скорости

Хиюх = max x^t), при этом средняя скорость передачи за время сеанса связи Т задается следующим образом

1 т xCp = m = Л/[х(О] = — J x^dt.

p          To

На рис. 1 приведена реализация случайного процесса x t         Т одного сеанса.

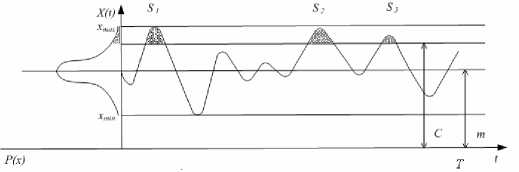
Рис. 1. Преобразование источника с изменяющейся скоростью в источник с постоянной скоростью передачи

Например, с помощью кодирования можно преобразовать скорость передачи, генерируемую источником с изменяющейся скоростью передачи (ИСП) в скорость с фиксированным значением. В результате этого в те промежутки времени, когда скорость, необходимая источнику, превышает скорость, представляемую сетью, происходит снижение качества обслуживания, и наоборот – если скорость передачи, предоставляемая источнику, больше требуемой, то это приводит к нерациональному расходу сетевых ресурсов.

Выбор величины разрешенной скорости передачи в данном случае является оптимизационной задачей, решение которой не может быть осуществлено в общем виде в силу невозможности определить нижнюю границу этой скорости ( x_min ). Чтобы оценить уровень снижения качества, связанного с потерей информации, установим заданный уровень разрешенной скорости передачи С, превышение которого случайным процессом и определяет потерю информации в сети.

Постановка задачи

В первом разделе показано, что снижение качества обслуживания происходит при ограничении пиковой скорости С<х , а снижение эффективности использования пропускной способности канала путем передачи фиктивной информации при выборе скорости передачи равной С =х (см. рис. 1). В реальных условиях разрешенную скорость передачи можно выбрать в виде уровня С при условии x_min <  C <  x_max , поддерживая эффективность и качество сети в определенных пределах.

Целью статьи является определение аналитических значений величины потерь информации, как вероятности пребывания процесса x ( t ) над заданным уровнем С . Вероятность пребывания процесса над уровнем С можно определить произведением среднего числа пересечений уровня С процессом x ( t ) в единицу времени N ( c ) на среднюю площадь выброса S , если принять общую площадь под кривой x ( t ) за единицу:

P(S > С) = N⁺(с) ■ S ср, (1) где условие S > C означает площадь процесса над уровнем С . В этом случае вероятность P(S > C )оп-ределяет величину потерь информации.

Определение среднего числа выбросов в единицу времени

Такая задача может быть решена на основе теории выбросов случайных процессов [3]. Ре- ально случайные процессы представляют собой непрерывные функции времени с ограниченным спектром в силу инерционных свойств, как самого источника сообщений, так и устройств обработки, действующих как фильтр нижних частот. В частности, понятия краткие и длительные сообщения и паузы между ними относительны и зависят от быстродействия средств реализации систем коммутации. Источник трафика считается пульсирующим, если суммарное время на установление и разъединение сквозного канала меньше интервала появления следующего сообщения. Эти соображения дают основания при выводе основных формул пользоваться параболической аппроксимацией. Такие функции имеют конечное число максимумов и минимум на ограниченном интервале времени Т. Это означает, что реализация x(t) может несколько раз пересекать уровень С (с положительной производной). Число таких пересечений соответствует числу положительных выбросов над уровнем С, для которого существует достаточно строгое математическое выражение [4]

Т со

Л' (С,Т) = \dt \x(t)P(c,x) d х,      (2)

о о где точка над независимой переменной x означает дифференцирование по t.

Для стационарных случайных процессов формула (2) значительно упрощается

ОО

N4C.T) = Р(С) \хр (jt) dx .        (3)

о

Это выражение позволяет определить среднее число выбросов в единицу времени для произвольного закона распределения стационарного случайного процесса x ( t ).

Если стационарный процесс имеет гауссово распределение, то среднее число выбросов в единицу времени составит [3]:

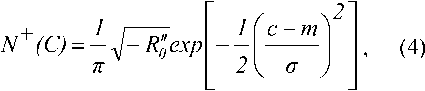
МтА где R^ = ^ – коэффициент корреляции; R" – вторая производная от коэффициента корреляции в точке г = 0; а – среднеквадратическое отклонение рассматриваемого процесса.

Определение средней площади выброса

Исходя из общих соображений,можно утверждать, что среднее число выбросов равно среднему числу максимумов, превышающих уровень С и при высоких уровнях основная часть выбросов имеет малую длительность .Дифференцируемый случайный процесс x(t) в небольшой окрестности максимума можно аппроксимировать параболой. В момент появления положительного выброса t0 справедливо равенство x(t0) = C при x(t0) > 0.

Разлагая функцию x ( t ) в ряд Тейлора в окрестности точки t₀ и ограничиваясь квадратичным членом, получим

P(S,C)ds =

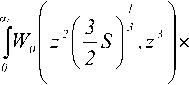
xz4 dz-

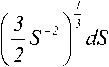
Получим искомую плотность вероятности

i 3 p H Г

P ( S , C )

7 0

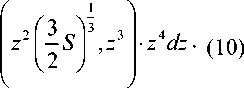
х(П = Ж) +х(У (/-/₀) +-x(z_o) kt — t^ ². (5)

Обозначив через длительность положительного выброса, получим                   и с учетом (5)                               отку да получаем

, _: 2х(/₀) , Ж)

Площадь выброса S можно определить так

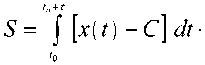
При нормальном стационарном процессе и высоких положительных уровнях С плотность распределения площади выброса

1 -

P(S,C) = -23S 3

exp --^(/LS1^ ,

где x =--;----, при (С » ст i^^r;

Для вычисления уравнения (9) использовано условие, что первая производная в момент начала выброса при нормальном исходном процессе распределена по релеевскому закону,

Пользуясь параболической аппроксимацией с учетом (5), получаем

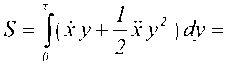
2^

а также условие i0 =

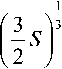
•«су.

Плотность вероятности площади выбросов P ( S , С ) ищется в предположении, что известна совместная плотность вероятности для первой и второй производных в момент начала положительного выброса на заданном уровне С . Путем замены переменной на S согласно равенству                 которая следует из

(7), имеем

Найдем среднее значение площади выброса

SCP = M[P(S,C)L

Формула (1) с учетом (2) и (12) примет вид:

т ^

В = P(S > С)= ^dt- ^У х(1) P(C,x)dх х

Wo( хо,хо Ydx-d х = W

з

Л,

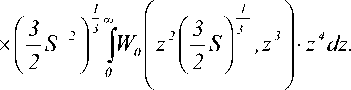
L\ls-2r

3 2     "

з dS dxo.

Для стационарного нормального процесса выражение (1) с учетом (4) и (12) принимает достаточно компактный вид:

Заменим переменную

и проинтегри-

руем правую часть равенства (8) по всем возмож-

74S >0=1,81^

^ГС-mY¹ 2 у o' J

ным значениям z :

Особенностью выражения (14) является независимость от корреляционных свойств нормального (гауссовского) процесса.

Учет сглаживающего влияния буферов на характер построения очередей

Рассмотренная методика позволяет определить потенциальные возможности сети по передаче информации с заданной скоростью (уровень С ),учи-тывая связанные с этим потери информации,зада-ваемые величиной превышения заданного уровня С (формула (13)).Однако в реальных условиях передача информации должна быть своевременной и без существенных потерь.Традиционно снижение потерь информации осуществляется путем буферизации. При коммутации флуктуирующий процесс оказывается всегда сглаженным в силу интегрирующих свойств коммутационных устройств,тем более,что при пакетной коммутации для организации процесса состязаний создаются искусственные буферы памяти для организации очередей пакетов.В этом контексте интересует поведение хвостов распределения длины очереди Q для каждого сервера в состоянии P ( Q ≥ B ) при заданном объеме буфера В .Рассмотрим трафи-ковый поток,подаваемый на детерминированный сервер,и поставим задачу,чтобы при этом выдерживались заданные ограничения производительности. Ограничения производительности,связанные с построением очередей,включают ограничения на такие статистические характеристики,как величина средних значений,вероятности переполнения буферов и др.Данный подход имеет преимущества в том,что он основывается на реальных критериях производи-тельности,а не на статистических характеристиках трафика.

Пусть трафиковый поток использует канал с вместимостью буфера В и пропускной способностью С . Рассмотрим очередь отдельного сервера (рис.2),при-чем ИСП – трафик в виде потока пакетов выступает в качестве стохастического процесса F ( t ) поступлений; m ( t )– размер очереди буфера.Если очередь обслуживается с постоянной скоростью V ,то в любой момент времени ее можно вычислить по формуле

Интегрируя (15), найдем время переполнения буфера где F cp             – среднее значение трафика

4 0

за время tk, m₀ – начальное состояние буфера.

Анализ показывает, что уже в процессе преобразования битового потока в поток пакетов, выходной трафик оказывается самоподобным, что оказывает существенное влияние на производительность сети. Более того, в [5] утверждается, что если на узел, обладающий памятью, поступает поток пакетов заведомо пуассоновского характера, то на выходе узла формируется процесс, обладающий фрактальными свойствами. Пусть поток пакетов представляет собой самоподобный процесс с плотностью распределения Р ( τ ), показанной на рис. 3.

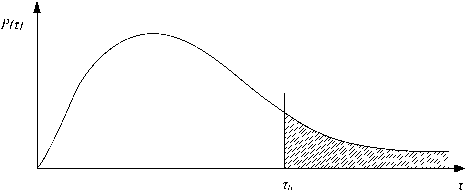
Рис. 3. Плотность вероятности с тяжелым хвостом

Вероятность превышения уровня τ > τ ₀ согласно рис. 3 равна

P(r > r₀) = jP(r)dT.

Трафиковые потоки с долговременной зависимостью с учетом (16) при условии, что 4 ^{T T}0’ приводят к распределениям вероятностей хвостов

A вейбулловского типа при mo = 0, где           – показатель качества,                   Fcp c

^^- = F(t)-C dt

полученной из модели, приведенной на рис. 2.

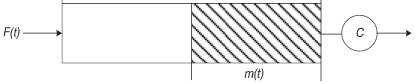
Рис. 2. Очередь отдельного сервера

P(Q > В) = exp(-y В^р), при 5 —»■ co. (17)

При β = 1 формула (17) приводит к экспоненциальному распределению хвостов.

Полученная зависимость ставится в основу концепции эффективной пропускной способности, когда управление доступом или распределяемая емкость канала обслуживания основана на распределении вероятностей хвостов. В этом случае предполагаемая емкость буфера определяется соотношением (13).

Заключение

Наосновеисследованийхарактерапостроений очередей, когда на сервер подается долговременно зависимый трафик (ДВЗ), в [5] делается вывод о том, что ДВЗ имеет незначительное влияние на емкость буфера и Q0 S в реальных условиях. Это объясняется тем, что уменьшение емкости буфера снижает память системы, и, следовательно, устраняет последствия воздействия на систему ДВЗ. Эти результаты являются дискуссионными, однако исследования, проведенные авторами, подтверждают сделанные в [5] предположения. Результаты этих исследований опубликованы в [4] для системы массового обслуживания M/M/m/n, осуществленные классическим методом, и для трафика-ДВЗ – методом статистических испытаний (Монте-Карло). Проведенные испытания показали, что при моделировании систем связи для достижения положительного эффекта необходи- мо варьировать не объемом буферов m, а числом каналов n в каждом направлении передачи информации.