Количественное сравнение дуальных схем электрических цепей

Для количественного сравнения дуальных схем сначала нормируются, а потом приравниваются соответствующие коэффициенты систем уравнений контурных токов исходной и узловых напряжений дуальной схем, что приводит к обратным схемам электрических цепей. Также приводятся вытекающие из обратности свойства 1×2- и 2×2-полюсни-ков.

Постановка задачи

Дуальными будем называть схемы, система уравнений контурных токов одной и узловых напряжений другой дуальны при выборе системы контуров и независимых узлов в соответствии с алгоритмом Кирхгофа. При этом ограничимся планарными схемами без магнитных связей.

Система уравнений контурных токов исходной схемы имеет вид:

[ Zik ][ - i ] = [Ei ],                    (1)

где Z ik — собственное контурное при i = к и взаимное контурное при i Ф к сопротивления, I i и E i соответственно контурный ток и контурная ЭДС i -го контура.

Система уравнений узловых напряжений дуальной схемы имеет вид:

[ y:. ][ u , ] = [i« ] . (2) где Y k — собственная узловая при i = к и взаимная узловая i ^ к проводимости, U i и 1 _3i - узловое напряжение и узловой задающий ток i -го независимого узла (штрихом отмечаются проводимости и элементы дуальной схемы).

Схемы электрических цепей можно сравнить по структуре и количественно. Структуры дуальных схем дуальны, соответственно дуальны графы этих схем, а матрицы инциденции узлов и ветвей [ A ] и контуров и ветвей [ B ] равны:

[A]=[B] ■ (3)

Количественное сравнение можно было бы установить между элементами матриц [ Z _k ] и [ Хк ] в уравнениях (1) и (2), однако элементы этих матриц имеют разные (противоположные) размерности.

Решение

Это препятствие можно устранить путем нормирования элементов матриц (матрицы [ Z ik ] по сопротивлению, а матрицы [ Y k ] - по проводимости).

С целью нормирования разделим обе части уравнений (1) на нормирующее сопротивление R 0 , а уравнение (2) – на нормирующую проводимость G 0 :

[zik ]=[y ],              (8)

откуда следует и выражение нормированных ве-

личин элементов

Rz  -   Lz  -- ikik

„    Rik,  „     Lik, CikR 0

R 0

Ст'         Г'-

G

G ik ’         Cik ’ LikG

G0

где чертой сверху отмечены нормированные элементы.

Выразим элементы дуальной схемы через элементы исходной схемы и коэффициенты нормирования:

G ik = ^0 Ra , C k = ^0 La , L k =    Ca ■ (9)

R ₀ R ₀ R ₀

Если приравнять

G0 ■1^0 ■

то формулы (9) принимают вид соотношений

между элементами обратных схем

1 R ₀           2

ik                  „    , ik 0 ik ,

^G ik    ^R ik

C' - Lik ik    R20

■

где

E i

R 0

^I зi

,

G′0 ⎥⎦

Такимобразом,свойствомобратныхсхеммож-но считать наличие двух матричных равенств: равенства матриц инциденции (3) и равенство нормированных матриц контурных сопротивлений и узловых проводимостей (8) при обратности нормирующих коэффициентов (10).

Итак, две схемы обратны, если их матрицы находятся в соотношении:

Z_a = Z,,/R_o = R k + рЛ^к + ik         ik 0

R ₀ R ₀

R ’

[A] = [ B]

Yk = Ya /G O = GT+ 7 ®C7 + G O      G O

Mk GO

при G 0 = VR о ■

Решим уравнения (4) и (5) для обратных

i = 1; 2 ... n , k = 1; 2 ... n ■

схем

После нормирования элементы матриц [ Z_k ^| и ^ Y/ k ^| становятся безразмерными и матрицы можно сравнивать.

⎡⎣Ii⎤⎦=⎡⎣Zik⎤⎦⎢i⎥⎪⎪ ⎣R0 ⎦

[ Ui ] = [Yik ]-1 [ R 013i ].

Сравнение, как известно, можно осуществить, соединяя сравниваемые объекты знаками больше (>), равно (=) и меньше (<). Будем сравнивать элементы матриц ⎡⎣ Z _ik ⎤⎦ и ⎡⎣Y _i ^′ _k ⎤⎦ и сами матрицы,

где ⎡_⎣Z _ik ⎤_⎦ и ⎡_⎣Y _i ′ _k ⎤_⎦ – обратные матрицы, соответственно I Z ik I и I Y ik I ■ Если параметры ис-

используя знак равенства

точников связать соотношением E _i R ₀ = I _зi или E = R ₀ I _зi , то равенства (12) принимают вид

⎡⎣ I i ⎤⎦=⎡⎣ Z ik ⎤⎦⎡⎣ I зi ⎤⎦ ,

[ Ui] = [ Y J-1 [ R 0- 3i ] , откуда

[ U i] = R 0 [ I ] .                (13)

Обратимся далее к сравнению комплексных мощностей, для чего составим выражение баланса комплексных мощностей исходной и обратной схем [1]:

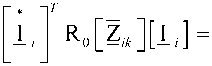
L [ E i ] =

n

= _Z I, E i e ^{j (} ' ’”⁾

i = 1

* "IT 1___ Г* IT.    ,

Ui.  ^ [ Y ][ Uj = Ui.   [i,] =

• -I R 0                L J

n

= Z UI i=1

p j ⁽ V 3i “V u ) з e

Модули и аргументы правых частей (14) и (15) равны, откуда комплексные мощности обратных схем эквивалентны.

Далее рассмотрим соотношение параметров обратных 1×2- и 2×2-полюсников (двухполюсников и четырехполюсников).

На рис. 1 показаны исходный (а) и обратный (б) 1×2-полюсники. Контуру, включающему зажимы, дан номер 1, также номер 1 дан узловой паре, образующей входные зажимы. Тогда Z _вх первого

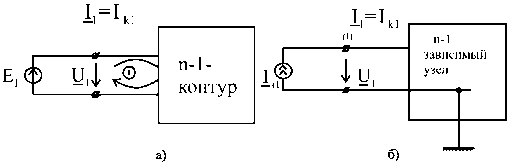
Рис. 1. Исходный и обратный 1×2-полюсники

• 7,  = E ¹       ^ k-

• —вх1 T 0 -T ,

11       A11k и входная проводимость обратного

I 31 ^A у 1 =--=--=— =---.

U 1    R 0 A liy    Z bx2

где Δ _k и Δ _11k – определитель и минор нормированной матрицы собственных и взаимных кон т урных сопротивлений исходной схемы, Δ _у и Δ _11у – то же самое нормированной матрицы узловых напряжений обратной схемы.

Тогда

Z bx1 • Z bx2 = R 0 .                 (16)

Выражение (16) определяет свойство входных сопротивлений обратных 1×2-полюсников.

На рис. 2 показаны исходный (а) и обратный (б) 2×2-полюсники.

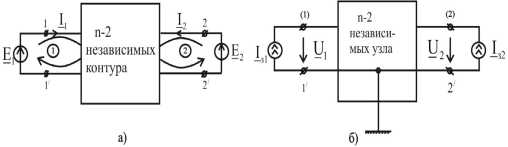
Рис. 2. Исходный и обратный 2×2-полюсники

Рассмотрим соотношение параметров холостого хода (ХХ) и короткого замыкания (КЗ) исходного и обратного 2×2-полюсников:

Z 1x ⋅ Z 1 ′ k =R 0 ² ,Z 1k ⋅Z 1 ′ x =R 0² ,⎫⎪

⎬

Z 2x ⋅ Z′ 2k =R 0 ² ,Z 2k ⋅Z ′ 2x =R 0² .⎪⎭

Цифровые индексы «1» и «2» указывают на пару зажимов, соответственно 1-1^′ и 2-2^′ , буквенные индексы «х» и «к» – на режим нагружения второй пары зажимов, соответственно «холостой ход» и «короткое замыкание», отметка «штрих» указывает на принадлежность параметра обратному 2×2-полюснику.

Из соотношений (17) следует, что характеристические сопротивления исходного и обратного 2×2-полюсников обратны [2]:

Z ci • Z C1 = R 2 uZ c2 • Z C2 = R 0 , (18)

а характеристические меры передачи равны:

Г с = Г С . (19)

Далее, пользуясь рассматриваемым приемом количественного сравнения дуальных схем, можно показать, что обратные 2×2-полюсники имеют равные рабочие меры передачи:

г р = г р . (20)

если обратны нагрузочные сопротивления слева R ₁ и R ₁ ′ , а также справа R ₂ и R ^′ ₂ также обратны:

R 1 • к ; = R 0 и R 2 • R 2 = R 2 .        (21)

Заключение

Следует отметить существование 1×2-полюс-ников, у которых сопротивления находятся в соотношении обратности, а схемы недуальны.