Коллектив непараметрических регрессий, основанный на декомпозиции обучающей выборки

Использование непараметрических моделей и алгоритмов, основанных на оценках плотности вероятности типа Розенблатта–Парзена, является одним из активно развивающихся направлений теории обучающихся систем. Эти модели и алгоритмы позволяют создавать типовые информационные средства, адаптируемые к условиям функционирования объектов различной природы. Однако при увеличении объема обучающей выборки вычислительная эффективность непараметрических статистик снижается. Подобные ситуации часто встречаются, например, при обработке больших массивов аэрокосмической информации. В этих условиях использование традиционных непараметрических моделей приводит к значительным временным затратам на формирование решений, в связи с чем возникает необходимость в разработке методики синтеза и анализа коллектива непараметрических регрессий, основанного на декомпозиции обучающих выборок по их объему.

Синтез коллектив а н епараметрических регрессий. Пусть V = ( x i , yⁱ , i = 1, n ) - выборка, составленная из n независ и мых наблюдений случайных величин x = ( x_v , v = 1, k ) и у , распределенных с неизвестными плотностями вероятности p ( x , y ) и p ( x ) >  0. Вид однознач-

C_v ( j' ), v = 1, k - коэффициенты размытости ядерных функций, значения которых убы ваю т с ростом количества элементов n множеств I j = 1, T . Здесь и далее бесконечные пределы интегрирования опускаются.

Рассмотрим ряд модификаций статистической оценки зависимости (1):

- среднее значение у_] = ф _j ( x ) , j = 1, T . В качестве приближения у = ф ( x ) по статистической выборке V используется статистика

1 ^T

у =ф( x ) = -ZX-(х).

T j =1

Оптимизация частных непараметриче ски х регрессий (2) по коэффициентам размытости c _v , v = 1, k , ядерных функций осуществляется в режиме «скользящего экзамена» исходя из условия минимума статистической оценки точности аппроксимации зависимости (1)

W j = —Z ( у ' ^-ф j ( x t ) ) n j ' ^е lj ___

При формировании слагаемых W j ситуация ( x ' , у ' )

.

ной стохастической зависимости у =ф( x,,..., x )

априори не задан.

Разобьем выборку V на T групп наблюдений Vj = (xi, yi, i е Ij), j = 1, T . Здесь Ij - множество номеров наблюдений переменных (x, y), составляющих j-ю T группу, причем U Ij = I = (i = 1, n).

j =1

На основании каждой выборки V_j осуществим синтез непараметрической регрессии [1]:

исключается из процесса обучения в выражении непараметрической регрессии (2);

- средневзвешенное значение у j, j = 1, T . В этом случае обобщенная модель искомой зависимости формируется в соответствии с выражением

T

у=Еа-ф/ x), j=1

w где aj = T

Z W - ¹ ' =1

–

весовые коэффициенты частных непа-

z у пф yj=ф-( x >=i'Ij   k",

2Пф[ i е Ij v=1     V j = i?T,

x v - x v

cv ( j )

x v ^- x v ) ’

cv ( j )

где Ф( u ) – ядерные функции, удовлетворяющие условиям H :

Ф( u ) = Ф(- u), 0 <Ф( u )<«,

раметрических регрессий ф _j ( x ) , j = 1, T , сумма которых равна единице;

– оценивание наиболее вероятного значения искомой зависимости. Будем полагать, чт о значе ние T достаточно для оценивания по выборке у „ j = 1, T , плотности вероятности частных решений p ( у ) при конкретном значении x . Для этого используем непараметрическую оценку плотности вероятности типа Розенблатта– Парзена [2]:

J ф ( u ) du = 1, J u ² Ф ( u ) du = 1,

p ⁽ y ) = Tc ^{Z ф}

у ^- У j

c

.

Jum Ф(u)di

Выбор оптимального параметра с статистики (4) осуществляется по условию максимума функции правдоподобия

L(c ^flp (y').

i =1 ^X '

При вычислении значений p ( у ) в соответствии со статистикой (4) полагаем i * j .

Наиболее вероятное значение y находим по условию у = argmax p (у), используя численные методы поиска экстремума – максимума оценки плотности вероятности p (у).

Асимптотические свойства коллектива непараметрических регрессий. Без существенной потери общности рассмотрим асимптотические свойства статистики (3) для случая, когда x – скаляр и вид плотности вероятности p ( x ) известен. В этих условиях справедливо следующее утверждение.

Теорема. Пусть ф ( x ), p ( x , у ), p ( x ) * 0 и первые их производные ограничены и непрерывны; ядерные функции Ф( u ) е H ; последовательности c j = c ( n j ) коэффициентов размытости ядерных функций таковы, что при n j ^ » значения c ( n j ) ^ 0, а значения nc ^ » , j = 1, T . Тогда при конечных значениях T коллектив непараметрических регрессий (3) обладает свойством асимптотической несмещенности и состоятельности.

Д о к а з а т е л ь с т в о. По определению имеем

M ( ф ( ^x ) ) = 7 Е M ( ф . ( ^x ) ) =

1 _T             ^j _Г - )

=у Е ( c /¹ p ^{( x} ) )¹ j ф ⁽ t ^{) ф} ^1 p ⁽ t ^{) dt} ,

T . =1                           v ^c j j

/ \ Г у )

где ф ( t ) = M I — I ; M - знак математического ожидания.

V x J

Проведем в интеграле замену переменных ( x - 1 ) c ^-- ¹ = u и, разлагая функции ф ( x - c j u ), p ( x - cu ) в ряд Тейлора в точке x , с учетом свойств ядерной функции Ф( u ) получим

W₁ = M ( ф ( x ) -ф ( x ) ) ~ А^ ( x ) х

1T1T ху£cj+ A(xъЕcj.

T i =1                       T i =1

Здесь

A ( ^x ) = ( ф ( ^x ) p ( ^x ) ) ⁽²⁾ /( ² p ( ^x ) ) ,

A ² ( x ) = p ^<2) ( x ) ф⁽²⁾ ( x ) j u ⁴ф ( u ) du Д 4 p ( x ) ) , где p ⁽²⁾( x ), ф ⁽²⁾( x ) - вторые производные по x соответствующих функций.

Отсюда при выполнении условий c ( n j ) ^ 0 и n j ^ » следует свойство асимптотической несмещенности статистики (3).

Для доказательства состоятельности оценки у = ф ( x ) вычислим ее дисперсию:

Исследуем асимптотические свойства среднеквадра- тического отклонения:

= E M

T ²

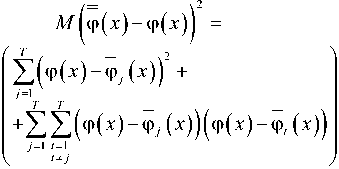
. (6)

С учетом результатов исследования асимптотических свойств традиционной непараметрической регрессии, пренебрегая величинами малости cj/nj , c2c,4, j = 1, T, t = 1, T, приведем выражение (6) при достаточно боль- ших значениях nj, j = 1, T, к виду

T ²

T

Е j =1

M ( ф ( x ) -ф ( x ) ) =

I ^{ф (} u < ^ф1; x ⁾ + c ⁴ ( а 1 ( x ) ) 2

n j c j p ( x )         ^{v 2}

TT

+ ( A ' ( x ) ) ² ЕЕ c 2 ,

.

Нетрудно заметить, что при выполнении условий c(nj) ^ 0 и njcj^ » при nj^ », j = 1, T, коллектив непараметрических регрессий (3) сходится в среднеквадратическом отклонении, а с учетом свойств асимптотической не- смещенности является состоятельным.

Сравнение аппроксимационных свойств коллектива непараметрических регрессий и традиционной непараметрической регрессии. Рассмотрим соотношения между асимптотическими смещениями, среднеквадратическими отклонениями и дисперсиями непараметрической регрессии у = ф(x) и у = ф(x) при оптимальных значениях коэффициента размытости ядерных функций.

Асимптотическое выражение смещения для непараметрической регрессии при x е R ¹

Г - ^

^у = ^у ( x ) = ( ncp ( x ) ) Е у ' ^ф| — I       ⁽⁸⁾

'=1       V c J имеет вид [3]

W, = M(

Оптимальное значение с* статистики (8), минимизи- рующее асимптотическое выражение среднеквадратического отклонения jM (ф(x)-ф(x))2 dx ,              (9)

определяется по формуле

1/5

. ЙНu )ll jф2 (x) p (x) dx c = -------------------2---------- , n j (A1 (x)) dx где |ф(u)|| =jф2 (u) du .

Для получения ана лит ически значимых результатов примем n j = n/T , j = 1, T . В этом случае оптимальные значения c ( n j ) = c ( n/T ) = c частных непараметрических регрессий ф j ( x ) , j = 1Д , в смысле минимума критерия типа (9) имеют вид c = c * T^1/5 .

Нетрудно показать, что при оптимальных значениях коэффициентов размытости разность между W ₁ и W ₂ дана выражением

A W 21 = W 2 - W 1 = ( c *) ² ( 1 - T^2/5 ) x x[ a ' ( x ) + A ² ( x ) ( c * ) 2 ( 1 + T^2/5 ) ] .

Знак A W ₂₁ определяется разностью ( 1 - T^2/5 ) <  0 при T >  1, т. е. смещение обобщенной непараметрической регрессии ф ( x ) больше, чем ф ( x ) .

Как и сл е довало ожидать, при T = 1 асимптотические смещения ф ( x ) и <р ( x ) одинаковы.

При разбиении исходной выборки на T групп точек одинакового объема n / T асимптотическое выражение

критерия

W3 =J M(ф(x)-ф(x)) dx при оптимальных коэффициентах c ядерных функций преобразуется к виду

(Г

IIФ ( и )| 12 / ф2 ( x ) p "1 ( x ) dx

1/5

^W 3 ^~

n

1 + T ² = W 1 + T¹ _T 6/54 _T 6/5

.

X

При этом W ₃ связано с асимптотическим выражением W ₄ критерия (9) для традиционной непараметрической рег-

рессии соотношением

W3 = —.. W.

3_{2 T} 6/5 4

Тогда

W4 = 2 T^6/5

W₃ = 1 + T

что подтверждает несколько большую эффективность в среднеквадратическом отклонении непараметрической регрессии (8) по сравнению с коллективом (3), например при T = 2 отношение (11) равно 0,92, а при T = 3 – 0,75.

Вместе с тем дисперсия статистики (8) больше, чем дисперсия коллектива непараметрических регрессий (3).

В этом нетрудно убедиться, если сравнить их главные дисперсионные составляющие в асимптотическом выражении критерия (9) при оптимальных коэффициентах раз-W мытости в W6 и значение W5 = T^^- в соответствующем выражении критерия (7). Их отношение

WL = t > 1, у T >  1.

W 5

Как и следовало ожидать, коллектив непараметрических регрессий (3) характеризуется меньшей дисперсией по сравнению со статистикой (8).

Коллектив непараметрических регрессий, основанный на декомпозиции обучающей выборки по объему, обеспечивает возможность использования технологии параллельных вычислений при восстановлении многомерных стохастических зависимостей. Установлено, что этот коллектив имеет асимптотические свойства, а его дисперсия значительно меньше дисперсии традиционной непараметрической регрессии.