Комбинированное решение однородных распределительных задач на основе модифицированного алгоритма Романовского и селективно-перестановочного алгоритма

Введение. Однородная распределительная задача (ОРЗ) является одной из основных комбинаторных задач в классической теории расписания (КТР). Она представляет собой упрощённую и абстрактную форму любой распределительной задачи. Однако в своей общей постановке ОРЗ является NP-полной задачей с показательным ростом сложности при увеличении размерности.

Методы решения задач КТР делятся на две большие группы: точные и приближённые. Ресурсные возможности точных методов, имеющих экспоненциальную сложность решения, сильно ограничены. Поэтому в последние годы много внимания уделяется приближённым методам, которые даже при невысокой точности приближения к оптимальному результату остаются востребованными благодаря низкой ресурсоёмкости решения РЗ.

Одной из наиболее популярных и перспективных тем исследований в области ОРЗ является повышение точности работы приближённых алгоритмов, привлекательных высокой скоростью решения РЗ.

Постановка задачи. Общая математическая модель постановки и решения ОРЗ будет подробно описана в следующей работе. В данной работе ставится задача улучшения точностных свойств быстрых приближённых алгоритмов без значительного ухудшения их ресурсных свойств. Платформой для такой модификации приближённых методов послужил метод селективноперестановочного подхода [1], разработанный для улучшения решений РЗ, полученных другими алгоритмами. Использование этого метода позволит повысить точностные показатели приближённых решений РЗ и, возможно, получить алгоритм их оптимизации. Наиболее перспективным в этом плане является модифицированный алгоритм Романовского. Поскольку этот алгоритм обладает достаточно высокими ресурсно-точностными характеристиками по сравнению с другими приближёнными алгоритмами.

Селективно-перестановочный алгоритм (СПА) решения ОРЗ. В СПА основным механизмом улучшения приближённого решения РЗ является выборочный обмен заданиями между исполнителями.

В работе [1] для удобства математической обработки решения РЗ вводится понятие «распределительная матрица» (РМ). РМ формируется на основе уже существующей таблицы распределения заданий по исполнителям путём добавления дополнительных условных заданий с нулевыми ресурсами. РМ имеет следующий вид:

М

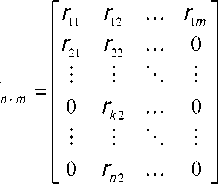
где л — количество заданий, m — количество исполнителей, г₈ — ресурс задания, назначенного >му исполнителю.

Тогда ресурсной характеристикой РМ является матрица-строка ^М ⁼ [^1  ^2  '¹] '

где Rj — загрузка >го исполнителя. Эта матрица-строка называется ресурсной строкой (PC) распределительной матрицы.

Каноническая форма распределительной матрицы (КРМ) должна удовлетворять следующим условиям.

• 1.    Элементы каждого столбца РМ располагаются в порядке убывания ресурсов назначенных исполнителям заданий.

• 2.    Столбцы РМ располагаются в порядке возрастания их ресурса загрузки R.

• 3.    При одинаковых ресурсах загрузки столбцы РМ располагаются в порядке возрастания их ресурсов в первых строках.

• 4.    При одинаковых ресурсах заданий в первых строках столбцы РМ располагаются в порядке возрастания ресурсов заданий вторых строк и т. д.

• 0. Стартовый этап состоит в получении таблицы распределения заданий и преобразовании её в исходную РМ, подлежащую оптимизации, и характеризующую её PC.

СПА состоит из предварительного стартового этапа подготовки математической модели РЗ и трёх последовательно повторяющихся функционально ориентированных этапов преобразования и анализа РМ.

• I.    Преобразование РМ к каноническому виду.

• II.    Постолбцовый относительно РМ и поэлементный относительно столбцов РМ параметрический сравнительный анализ ресурсов заданий исполнителей, наиболее перспективных для улучшающей оптимизируемую оценку перестановки.

• III.    Принятие и реализация решения:

• •    либо о перестановке заданий в РМ,

• •    либо об отсутствии в анализируемом варианте КРМ дальнейших улучшающих перестановок и завершении работы алгоритма улучшения РМ.

Более подробно рассмотрим II основной этап работы алгоритма. Сравнительный анализ осуществляется в соответствии со следующими правилами (Пр.):

Пр. 1. Поэлементный анализ заданий начинается со столбцов загрузки (СЗ), которые имеют наибольшую и наименьшую загрузки. Эти столбцы условно называются СЗ-донор и СЗ-клиент соответственно.

Пр. 2. Для рассматриваемых СЗ выбирается пара заданий, которая удовлетворяет условию ^Kd > 'id 'jc > '

где R_d — загрузка СЗ-донора, R_c — загрузка СЗ-клиента, г_и — ресурс задания СЗ-донора, r_jc — ресурс задания СЗ-клиента.

Если таких пар заданий несколько, то выбирается та пара, которая наиболее эффективно улучшает оценку решения РЗ.

Пр. 3. Если для рассматриваемых СЗ не найдена пара заданий, удовлетворяющих условию (1), то выбирается следующий для рассмотрения СЗ-клиент.

Пр. 4. Если просмотрены все СЗ-клиенты, то СЗ-донор помечается как бесперспективный и выбирается следующий СЗ-донор. И так до тех пор, пока не будут рассмотрены все СЗ-доноры. Сравнительный анализ эффективности алгоритмов решения ОРЗ. С целью изучения эффективности комбинированного решения ОРЗ на основе МАР и СПА осуществлён сравнительный анализ с такими приближёнными алгоритмами, как метод критического пути (МКП) и эволюционно-генетический алгоритм (ЭГА). Проведены вычислительные эксперименты при разных значениях параметров задачи. Такими параметрами являются: п — количество заданий, т — количество исполнителей, [z„z,] — диапазон генерации ресурсов заданий. В ходе экспериментов были случайным образом сгенерированы по 100 векторов ресурсов заданий в диапазоне [z_lf z₂]. В качестве эволюционно-генетической модели использовалась модель, описанная в работе [2]. Для анализа точностных характеристик рассматриваемых алгоритмов на малых размерностях ОРЗ использовался процент нахождения оптимальных решений Р_0ПТ, а ресурсных — среднее время выполнения алгоритма 1с_Р(в секундах) по 100 опытам (табл. 1).

Таблица 1

Результаты экспериментов на малых размерностях ОРЗ

т	п	k,z2]	МАР		МАР и СПА		МКП		ЭГА
			Ропт	tcp	Ропт	tcp	Ропт	tcp	Ропт	tcp
2	12	[50, 55]	100	<0.001	100	<0.001	94	<0.001	100	0.171
2	12	[30, 65]	100	<0.001	100	<0.001	36	<0.001	100	0.207
2	14	[50, 55]	100	<0.001	100	<0.001	92	<0.001	100	0.239
2	14	[30, 65]	100	<0.001	100	<0.001	51	<0.001	100	0.196
3	13	[40, 60]	99	<0.001	100	<0.001	0	<0.001	99	0.245
4	12	[50, 55]	100	<0.001	100	<0.001	85	<0.001	100	0.221
4	12	[30, 65]	92	<0.001	99	<0.001	36	<0.001	89	0.264
4	14	[50, 55]	100	<0.001	100	<0.001	0	<0.001	96	0.280
4	14	[30, 35]	99	<0.001	100	<0.001	0	<0.001	70	0.333

По результатам, приведённым в таблице 1, видно, что СПА является достаточно эффективным средством улучшения решений РЗ, поскольку практически во всех случаях улучшал решения, полученные МАР. Также СПА продемонстрировал низкие требования к ресурсам. Благодаря вышеуказанным достоинствам СПА, комбинированное использование его с МАР показало значительно лучшие ресурсно-точностные показатели, чем другие алгоритмы. Поскольку при неблагоприятных условиях совместное применение рассматриваемых алгоритмов позволило получить оптимальные решения в 99 % случаев, тогда как МАР — в 92 % случаев, ЭГА — в 70 % случаев, а МКП ни разу не позволил получить оптимум.

Также проведены эксперименты на более высоких размерностях ОРЗ: m > 3, п > 31. В ка честве показателя, оценивающего точностные характеристики алгоритмов, цент решений Рмин, имеющих минимальную оценку по опыту (табл. 2).

использовался про-

не улучшил оценку всех экспериментах

По результатам, приведённым в таблице 2, видно, что СПА ни разу решений, полученных МАР. Скорее всего, это обусловлено тем, что МАР во находил оптимальные решения, поскольку их оценка по минимаксному критерию (ММК) была минимальной по сравнению с решениями, полученными остальными алгоритмами.

Таблица 2

Результаты экспериментов на больших размерностях ОРЗ

m	n	k,z2]	MAP		MAP и СПА		МКП		ЭГА
			p ' мин	tp	p ' мин	tp	p ' мин	tcp	p ' мин	tcp
3	31	[50, 55]	1OO	0.023	1OO	0.023	0	<0.001	57	0.795
3	31	[30, 65]	1OO	0.001	100	0.001	0	<0.001	93	0.703
3	51	[50, 55]	1OO	0.018	100	0.018	89	<0.001	1OO	0.609
3	51	[30, 65]	1OO	0.002	100	0.002	73	<0.001	81	0.823
4	41	[40, 60]	1OO	0.092	100	0.092	0	<0.001	31	0.802
5	31	[50, 55]	100	0.010	100	0.010	0	<0.001	26	0.848
5	31	[30, 65]	100	0.001	100	0.001	0	<0.001	37	0.548
5	51	[50, 55]	100	0.087	100	0.089	0	<0.001	1	1.535
5	51	[30, 35]	100	0.002	100	0.002	0	<0.001	0	1.139

Выводы. Комбинированное применение МАР и СПА для решения ОРЗ невысоких размерностей (т<5, л<51) позволяет достигать достаточно высоких ресурсно-точностных показателей по сравнению с другими приближёнными алгоритмами. Поскольку по результатам проведённых экспериментов совместное использование рассматриваемых алгоритмов позволило получить решения с минимальной оценкой по опыту в 99,9 % случаев, тогда как ЭГА — в 74 % случаев, а МКП — в 31 % случаев. Применение СПА для улучшения решений РЗ малых размерностей в некоторых случаях позволило повысить точность МАР на 7 %. Однако на более высоких размерностях задач СПА ни разу не улучшил решения, полученные МАР, что, скорее всего, обусловлено высокими точностными характеристиками МАР. Поэтому целесообразность комбинированного использования МАР и СПА для решения ОРЗ высоких размерностей требует дальнейшего исследования.