Комбинированные некритические взаимодействия и синхронизмы при генерации оптических гармоник в нелинейных кристаллах ромбической сингонии на примере кристалла трибората лития

При генерации второй гармоники (ГВГ) лазерного излучения во многих практически важных случаях необходима реализация так называемых «некритических синхронных взаимодействий» (некритических фазовых синхронизмов), то есть таких синхронизмов, при которых эффективность преобразования не зависит (или зависит слабо) от температуры, длины волны, отклонения от углов синхронизма и др. Другими словами, под некритическим нелинейно-оптическим взаимодействием волн при преобразовании частоты лазерного излучения вдоль определённого направления в нелинейном кристалле понимается такое взаимодействие волн, при котором равна нулю хотя бы первая частная производная волновой расстройки A K по какому-либо выбранному параметру p , определяющему условия преобразования частоты. Такое взаимодействие назовём некритичным по параметру p , где параметр p может определять следующие величины: температуру T , длину волны основного излучения λ , азимутальный ϕ и полярный θ углы, напряжённость электрического E и магнитного B полей, механическое напряжение в кристалле t .

В первом приближении при некритическом взаимодействии волновая расстройка AK не зависит от параметра p, а ширина синхронизма по данному параметру равна бесконечности. Если одновременно выполняется условие дAK/dp = 0 и существует фазовый синхронизм (AK = 0), мы имеем некритический синхронизм по параметру p. В направлениях, вдоль которых осуществляются некритические нелинейно-оптические взаимодействия, необязательно выполняются условия фазового синхронизма, однако, если использовать в данных направлениях квазисинхронное взаимодействие, можно получить эффективное преобразование частоты и большие ширины синхронизма по параметру p. Значения ширин синхронизма с практической точки зрения очень важны. Например, при генерации второй и высших оптических гармоник (ГВГ, ГТГ, ГЧГ) расходящегося лазерного излучения (многомодовые твердотельные лазеры, полупроводниковые и волоконные лазеры с высокими значениями дифракционной расходимости и т. п.) нужны нелинейно-оптические элементы с большой угловой шириной синхронизма. Аналогично, значение спектральной ширины синхронизма важно при преобразовании частоты широкополосного лазерного излучения (лазеры на красителях, муль-тичастотные лазеры с одновременной ге- нерацией нескольких разностных частот, фемтосекундные лазеры). Температурная ширина синхронизма важна для создания «атермальных» (температурно-некритических) преобразователей частоты, не требующих применения нагревательных или охлаждающих устройств (такой синхронизм, в частности, был реализован в кристалле КТР в нашей работе [1], где была получена экспериментальная температурная ширина синхронизма при ГВГ 210 °C).

В данной работе на примере кристалла LiB ₃ O ₅ (LBO) рассмотрены некритические взаимодействия и некритические фазовые синхронизмы при ГВГ. Обсуждаются возможности практического применения таких ориентаций ( ϕ , θ ) нелинейного кристалла, для которых имеют место комбинированные некритические взаимодействия (например, одновременно по углам и температуре, одновременно по углам и длине волны и т. п.). Представлены результаты некоторых численных расчётов.

• II.    Некритические взаимодействия и синхронизмы при преобразовании частоты лазерного излучения в нелинейной среде

Для эффективного преобразования частоты лазерного излучения в однородном нелинейно-оптическом кристалле необходимыми и достаточными являются отличие от нуля эффективной нелинейности d eff и наличие фазового синхронизма [2]. Условием скалярного фазового синхронизма является равенство нулю скалярной волновой расстройки A K . Если p о — один из параметров θ 0 , ϕ 0 , λ 0 , T 0 , соответствующих выполнению условия фазового синхронизма (при этом волновая расстройка A K = 0), то при отклонении p от p о можно записать разложение (A p = p — p о ):

A K ( p ) = A K ( p 0 ) + A K AI A p + ∂p

1 d ² A K ( p о )      ₂

⁺ 2 dp 2 ^(A p ) ⁺ -      ⁽¹⁾

По определению фазового синхронизма AK (p0) = 0, однако формула (1) справед- лива для любого значения p0 , в том числе и не удовлетворяющего условию фазового синхронизма, в этом случае AK (p0) = 0.

Поясним понятия некритического взаимодействия и некритического синхронизма [1]. Под некритическим взаимодействием будем понимать такое взаимодействие волн, при котором первая производная в (1) равна нулю; тем самым утверждается, что при некритическом взаимодействии расстройка A K ( p ) в первом приближении не зависит от A р. Необходимость учёта второй производной в (1) в этом случае определяется соотношением между величинами второй производной и A K ( p 0 ). Если при этом также выполняется условие A K ( p 0 ) = 0, то мы имеем некритический синхронизм; тогда наибольшим членом в (1) становится вторая производная.

Аналогично, взаимодействие в общем случае будет критическим, если первая производная в (1) отлична от нуля (при этом вкладом второй производной в (1) в большинстве случаев можно пренебречь [1]). Если вдобавок выполняется условие A K ( p 0 ) = 0, то мы имеем критический синхронизм.

Зависимость коэффициента преобразования, например, для ГВГ, от A p в приближении заданного поля и плоских волн в общем случае определяется выражением [2]:

П (A p ) ~ sinc ²

/ A K ( p ) • l \

где sin cx = si Xx , l — длина кристалла.

В случае ^{д Л} K ^^p 0 ) = 0 (некритическое взаимодействие) имеем

П (A p ) ~ sinc ²

^^A K ⁽ p о ^{) +}

1 д ² A K ( p о ) ⁺ 2    dp ²

^(A p )²) l)-

Как уже указывалось, при A K ( p о ) = 0 мы имеем некритический синхронизм.

Заметим, что, если AK (pо) = 0, взаимодействие (критическое или некритическое) может быть переведено в синхронизм (соответственно, критический или некритический) при использовании кристаллов с регулярной доменной структурой (РДС-кристаллов) с периодом (длиной домена), кратной когерентной длине взаимодействия lk = дKpQ), и тем самым реализовать квазисинхронное взаимодействие (квазисинхронизм, см., например, [2]).

Большой практический интерес могут представить комбинированные некритические взаимодействия при преобразовании частоты лазерного излучения, то есть такие процессы, для которых одновременно реализуется два или более некритических взаимодействий, например, по двум углам ϕ , θ , по одному из этих углов и по длине волны, по длине волны и температуре, даже по всем 4-м параметрам и т. п. Как уже указывалось, возможное отсутствие в таких случаях фазового синхронизма может быть скомпенсировано использованием РДС-кристаллов. Очень важно при этом оценить величину эффективной нелинейности d _eff , которая определяет эффективность преобразования (напомним, что в приближении заданного поля п ~ d 2 ff , [1]). Это становится тем более актуальным, поскольку при некоторых комбинированных некритических взаимодействиях может оказаться, что d _eff весьма мала или даже равна нулю.

III.    Основные выражения

Ниже мы рассматриваем оптически двухосный кристалл LiB 3 O 5 (LBO), указательная поверхность показателя преломления которого является двуполостной поверхностью четвёртого порядка с четырьмя точками самопересечения (напомним [2], что для оптически одноосных кристаллов данная поверхность представляет собой две отдельные поверхности второго порядка — сферу и эллипсоид вращения, которые касаются друг друга в двух точках, определяющих оптическую ось кристалла).

Более сложная форма указательной поверхности показателя преломления для оптически двухосных кристаллов приводит к появлению новых свойств, которые отсутствуют для оптически одноосных кристаллов (например, некритичный температурный синхронизм и др.). Для одноосных кристаллов при удачном соотношении значений параметров некритичное взаимодействие также может иметь место, но только при каком-то одном соотношении пара- метров, в то время как в случае оптически двухосного кристалла эти свойства могут иметь место в некотором диапазоне значений рассматриваемых параметров. Это связано с тем, что вдоль всех возможных направлений синхронизма в двухосном кристалле, при прочих равных условиях, наблюдается большой спектр отношений скоростей изменения показателей преломления для взаимодействующих волн (например, при изменении температуры), тогда как в случае одноосного кристалла существует только одно значение отношения скоростей.

Одними из наиболее значимых параметров фазового синхронизма для практических применений являются ширины синхронизма. Введём параметр Z (Л Р ), по значению которого будем определять величину фазового синхронизма Л p :

ЛK (ЛР) • Л z (Лp) = sine2 (------2------J .

Под шириной синхронизма по параметру p будем понимать такое его отклонение Л p от значения p 0 , соответствующего выполнению условий фазового синхронизма, при котором значение параметра Z (Л p ) равно 0 , 5.

В том случае, когда условия фазового синхронизма не выполняются, Л K = 0, когерентную ширину взаимодействия по параметру p при реализации квазисинхронизма можно определить, используя следующее выражение:

(2Л p ) =

2( п/1 - Л K ) д Л K/dp

Видно, что чем меньше значение производной д Л K/dp , тем больше величина ширины взаимодействия по параметру p .

Рассматривая угловые ширины синхронизма, следует заметить, что для любых типов нелинейно-оптических взаимодействий всегда существует некоторая плоскость, в которой реализуется некритический угловой синхронизм. Данная плоскость содержит в себе направление, вдоль которого реализуется выбранный тип взаимодействия, и она может образовывать некоторый угол α с осью Z . В случае а = 0 ° мы имеем взаимодействие, некритичное по полярному углу θ , а при а = 90 ° — взаимодействие, некритичное по азимутальному углу ϕ .

При необходимости использования РДС-кристаллов следует учесть следующее. Волновая расстройка определяет когерентную длину взаимодействия l k = ^ к , а из-за того, что длина домена РДС-кри-сталла кратна l _k и должна находиться в определённых технологических рамках, само значение A K должно быть не слишком малым и не слишком большим, чтобы длина домена оказалась технологически приемлемой. При этом значение эффективной нелинейности d _eff должно быть ненулевым и не слишком малым.

IV.    Результаты и их обсуждение

Для кристалла LBO был выполнен расчёт направлений некритических взаимодействий и синхронизмов для процесса ГВГ. Основные параметры данного кристалла были взяты из работы [3]. Главные показатели преломления кристалла LBO определяются формулами Зеллмейера:

n X i ,х 2 ,х з =

V A ⁺ 1 2 —C ^- D ^2⁺

+ ( E • X + F ) • 10 " ⁶ • ( T - 20) , где λ — длина волны в микрометрах, T — температура в градусах Цельсия.

Соответствующие показателям преломления коэффициенты представлены в табл. 1.

Для расчёта значений эффективного коэффициента нелинейности использовались следующие значения нелинейных коэффициентов [3]:

d 31 = - 0,67,     d32 = 0,85, d33 = 0,04,     d24 = 0,85,     d 15 = - 0,67.

Введём понятие линии некритического взаимодействия по параметру p .

Под этой линией будем понимать линию на плоскости углов ( ϕ , θ ), определяющую совокупность направлений в кристалле, вдоль которых выполняется равенство d A K/dp = 0.

Линии некритических взаимодействий и линия синхронизма при ГВГ излучения YAG: Nd ³⁺ -лазера ( X = 1 , 064 мкм) по первому и второму типам взаимодействия в кристалле LBO показаны на рис. 1 и 2 соответственно.

На рис. 1 линией GBCF обозначена линия направлений синхронизма

(A K = 0), линия HBA — направления, в которых д A K/дТ = 0, на линии KDEd A K/дХ = 0, на линиях MAFEL и NPd A K/дф = 0, на линиях MGHKN, ACDQ и LQPd A K/d9 = 0. На рис. 2 на линии GF A K = 0, на линии HAd A K/дТ = 0, на линиях MAL и NPd A K/дТ = 0, на линиях MHGN, AQ и LQPd A K/dT = 0.

Точки пересечения линии фазового синхронизма с линиями нулевых производных A K по одному из параметров являются направлениями некритического фазового синхронизма по этому параметру, точки пересечения линий нулевых производных A K — направления, в которых реализуются взаимодействия одновременно некритические по параметрам, соответствующим пересекающимся линиям.

Поэтому, если необходимо установить возможность реализации некритического фазового синхронизма определённого типа по какому-либо параметру, следует определить совокупность направлений фазового синхронизма и совокупность направлений, в которых частная производная волновой расстройки по данному параметру обращается в ноль. Точка пересечения указанных линий определит направление синхронизма, некритичного по выбранному параметру, а точки пересечения линий нулевых производных A K определят направления, в которых реализуются взаимодействия, одновременно некритические по параметрам, соответствующим пересекающимся линиям. Основные характеристики точек пересечения указанных линий для кристалла LBO для типов взаимодействий ss-f и sf-f представлены в табл. 2 и 3 соответственно.

Точки, соответствующие некритичным фазовым синхронизмам на рис. 1, 2 обозначены буквами F, G, B, C. Это некритичные синхронизмы по следующим параметрам: азимутальному углу ϕ , полярному углу θ , длине волны основного излучения λ , температуре нелинейно-оптического элемента T соответственно. Отметим, что некритический по температуре синхронизм наблюдается только для взаимодействия по типу ss-f, при этом в окрестности длины волны X = 1 , 29 мкм в направлении ф = 23 ° , 9 = 61 ° существует синхронизм, одновременно некритичный как по температуре, так и по длине волны основного излучения.

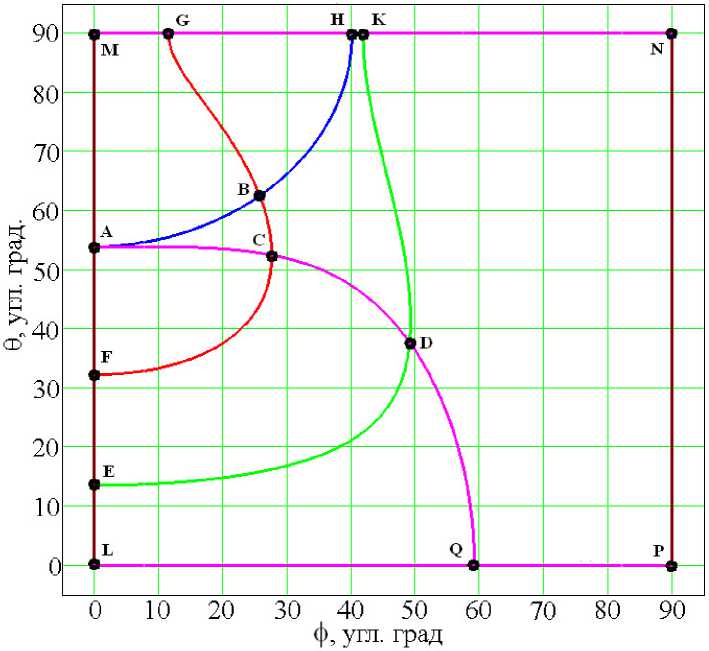
Рис. 1. Линия синхронизма и линии нулевых производных A K при ГВГ ( А = 1 , 064 мкм) на кристалле LBO по типу взаимодействия ss-f

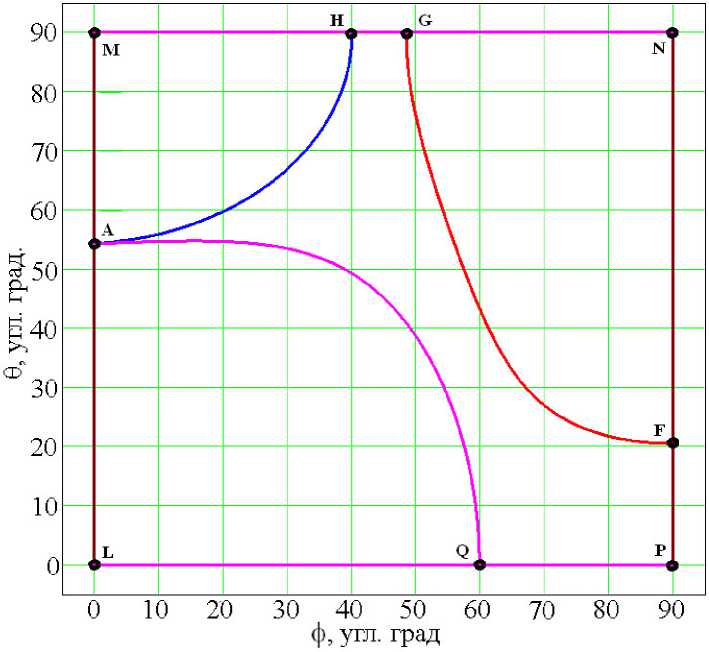
Рис. 2. Линия синхронизма и линии нулевых производных A K при ГВГ ( А = 1 , 064 мкм) на кристалле LBO по типу взаимодействия sf-f

Таблица 1

	ОО	ю со	СО erf
и	о	о	of
	ОС ОС со	ОС ^ ОС	5 ОС
Q
	со	о: ос	00 04 04
и
		04	СО
m
	04 of	О) 00 of	о ОС of
о
H Щ OJ У О	£	£	N £

W 2 X с 5S ф 2 S се со X 2 2 ^	7 л 7 S ^к	о		о	о	о	о	о
	7 л 7 s s со col	о	о	o’	о'	о	о	о
0 =
О m j	S S	m ^	со О1	со со	со 'СО	9 °1	о	со ОО
S л X	< со
	7 ^		7	7		о	7	7
m	7		о				о	с—-
t-i к ч ч: >s s X т о iS Ф 2 S се 00 X S	S X S	о	со^ <о	о	о	of	7 со	ОО °К со
	^к
	m ^ К 03	о	о	со 7		й^	о	о
	7		7		7		7	7
	S X	со ОО 7				о 7
и 0 2 к S К 0 л X X х ф X х х Ф У S т х Л X ф х х х х т ф S Л Ф т X Л	<		со^ 7	к	of		-О 7	'СО 7
	се S ЕН S Он X	^Г XL < ко col ^к	<1 <О col		^к ^к ^к	^к XL <1 со col	^к XL <1 со col	^к <1 со col
	ф’	со °1 3	со 7. S S е	S со QO -о II	S ОС? со 9	о II	S S II	§
	се еЗ	<7	ь	о	м	S	X	£. О
	S;		см	со	хГ	1-0	со	Г-

to ^ X о 5S ф 0 m 5 s :-

7 ^ Л 7 < к

02 СМ

с

7

о

О

со (М °1 7

о

а

02

7 7

а

а

а

7 ^ Л 7

СО СО со_

со со_

о

со со

8 °1

ОС (М со

S СО^

о

<1 ко col

0 В

7

ОС 00

о m j ф ч ч н о S л я S tH “ ч ч »s S и г- « ф го М

^7 < ко со|

СО

со со

со

со

о

о

о

со (М со^

СО со^

02 7

со о 7

7 ^

7

7

7

7

7

7

7

7

7

о

о

о

о

о

о

о

о

< к

02 ОО со_

ОО т

7

ОС 7

00 7

со со^ 7

со

ОС оГ

со со °1

7

02 со^ 7

m в 05

о

02 со_ 7

7

СМ

о

(М

02 'СО

о

о

со 7

S

о

о

к

7

'СО со

8

o'

со (М

со 7

7

02 7

о 7 7

со

o'

В

S О г: S О Л X х х о X X о ф г X г-S л ф X X X го S л ф г л й

-ч <1

оЗ В Н 6 В н аЗ й

и

=0

=0

< к ф| II

II

II

II к св

ф|

^ к >

<к

< к

<1 ко col

<1 ко col

<1 ко col

< к >

<1 со col

<1 со col

II <1 со col

'СО

S со со со.

оГ СО II со 00^ см

сЧ со 02 СО_ (М

02 °1 оГ со со

02 II со 7

СО II со со~ 7~

СО 7 со

02 II со О1 со

(М °1 со

со оГ II

ХГ) со

S со

02 II со 02 II

II ф S II

аЗ В В 7

о

m

и

ь

Q

и

Ё

в

о

Za

&

S;

СМ

со

хГ

LO

со

ь-

00

02

о

<м

со

2

Следует отметить, что для каждого оптически двухосного кристалла и каждого типа синхронизма существуют свои длины волн, при которых наблюдается комбинированный некритичный по длине волны и температуре синхронизм. Нелинейнооптические кристаллы, обладающие таким комбинированным синхронизмом, могут успешно применяться, например, для преобразования частоты полупроводниковых лазеров, у которых, как известно, длина волны генерируемого излучения существенно меняется при изменении температуры лазерного диода.

При рассмотрении нелинейных взаимодействий, некритичных одновременно по нескольким параметрам, особого внимания заслуживают точки, обозначенные на рис. 1, 2 буквой А. В этих точках реализуются взаимодействия, некритичные одновременно по трём параметрам: азимутальному и полярному углам ϕ , θ ,а также по температуре T . Однако эффективный коэффициент нелинейности в данных точках равен нулю. Тем не менее, учитывая очень резкое изменение d eff в окрестности указанной точки, можно рекомендовать к практическому применению направления, образующие с направлением в точке А небольшой угол порядка одного, двух градусов (например, точки a 1 , a 2 (табл. 3)), однако следует учитывать, что при этом наблюдается столь же резкое изменение частных производ-

ТРУДЫ МФТИ. — 2009. — Том 1, № 2 ных волновой расстройки. Любопытным является поведение кривых, на которых д (A K) /дТ = 0 (кривая ABH на рис. 1 и кривая AH на рис. 2), именно то, что она проходит через точку пересечения линий, где д (a K ) /д^ = 0 и д (A K ) /дб = 0, находящуюся недалеко от оптической оси кристалла. Такое поведение не свойственно другим двухосным кристаллам (например, кристаллам семейства КТР); по-види-мому, это является косвенным следствием того, что коэффициенты термического расширения для LBO имеют различные знаки для разных осей.

В случае всех двухосных кристаллов к направлению, чрезвычайно близкому к точке А (для каждой длины волны существует своё направление точки А), стягивается конус направлений некритических взаимодействий по длине волны при её увеличении. Так, для ГВГ в LBO по типу ss-f на длине волны А = 1 , 744 мкм рассматриваемый конус вырождается в одно направление, лежащее в координатной плоскости XZ , и при дальнейшем увеличении λ пропадает. Здесь можно говорить о том, что в этой точке А наблюдается комбинированное взаимодействие, некритическое по четырём параметрам: углам ϕ , θ , температуре и длине волны.

Диапазоны длин волн существования некритичных по длине волны взаимодействий для кристалла LBO представлены в табл. 4.

Таблица 4

Диапазоны длин волн, где выполняется д А K/дХ = 0 для LBO

Тип взаимодействия	d ^ jK = 0, мкм	K = K = 0, мкм	д ^ К = 0, A K = 0, мкм
ss-f	0,88–1,74	1,07–1,744	1,26–1,31
ss-f	1,14–1,70	1,33–1,70	1,29–1,30

V.    Заключение

В работе рассмотрены комбинированные некритические взаимодействия и синхронизмы для ГВГ в кристалле LBO. Показано существование некритичного по температуре синхронизма при ГВГ излучения лазеров, работающих в ближней ИК-области. Продемонстрировано, что плоскость, в которой наблюдается максималь- ная угловая ширина синхронизма, не параллельна рёбрам нелинейно-оптического элемента, а образует некоторый угол с ребром, параллельным плоскости X1, X2 кристаллофизической системы координат. Отмечена возможность использования некритичного синхронизма в LBO одновременно по температуре и в некоторой области по длине волны лазерного излучения. Это явление можно использовать при преобразовании частоты излучения полупроводнико-

ТРУДЫ МФТИ. — 2009. — Том 1, № 2 вых лазеров, у которых длина волны излучения существенно зависит от температуры. Во многих случаях при комбинированных некритических взаимодействиях может отсутствовать фазовый синхронизм, что может быть скомпенсировано применением РДС-кристаллов, допускающих ква-зисинхронные взаимодействия.

Таким образом, подтверждено, что в двухосных кристаллах имеется возможность использования одновременно нескольких видов некритичного фазового синхронизма. К тому же некоторые новые двухосные нелинейно-оптические кристаллы, например, триборат висмута BiB3O6 (BiBO), обладают нелинейными коэффициентами, значения которых превосходят коэффициенты кристалла КТР. В наших дальнейших работах мы продолжим исследования двухосных кристаллов для выявления некритических взаимодействий и синхронизмов, представляющих практиче- ский интерес для перспективных преобразователей частоты лазерного излучения.

Авторы пользуются случаем поблагодарить доцента МГТУ им. Н.Э. Баумана С.Г. Гречина за полезные дискуссии и рекомендации, а также профессора ФФКЭ МФТИ А.А. Фомичева за поддержку данной работы.