Компенсация аберраций волнового фронта в телескопах космических аппаратов с регулировкой температурного поля телескопа

Компенсация аберраций волнового фронта телескопа, генерируемых оптикой самого телескопа, часто выполняется на основе экспериментально определённой функции рассеяния точки без применения специально предназначенного для измерения аберраций оборудования, каким, например, является датчик Шака–Хартмана.

С этой целью по полученной функции рассеяния точки (ФРТ) рассчитывают аберрации волнового фронта оптической системы. Для оптических систем, находящихся вблизи дифракционного предела, для этого был предложен метод фазового разнесения, предполагающий использование двух изображений не обязательно точечного источника с известной разностью аберраций [1]. Этот метод неприменим для изображений, получаемых в обычных телескопах, размер пикселя в которых соизмерим с изображением точечного объекта. Другой метод – метод обработки изображений точечных источников с помощью нейронных сетей [2] – в настоящее время применяют для систем адаптивной оптики, имеющей дело с изображениями, также полученными вблизи дифракционного предела. Здесь используется два изображения: одно фокальное и одно внефокальное.

Связь между распределением интенсивности в расфокусированном изображении и локальной кривизной волнового фронта описывается уравнением переноса излучения. Использование этого уравнения для восстановления аберраций, рассмотренное в [3], ограничено тем, что необходимо располагать двумя изображениями с относительно большими и равными дефокусами противоположных знаков.

В работе [4] было показано, что одного внефо-кального изображения точечного источника, полученного с помощью ПЗС-матрицы, достаточно для восстановления явных аберраций, если лучи от разных точек апертуры не пересекают друг друга.

В работе [5] представлен метод количественного определения оптических аберраций по одному расфокусированному изображению, основанный на использовании модели, представляющей аберрации с помощью разложения в ряд полиномов Цернике. Начальное приближение получается по результатам вычисления вторых моментов распределения интенсивности изображения точечного источника относительно геометрического центра изображения. Затем с помощью итерационной процедуры находятся более высокие аберрации. Основанная на данном подходе компьютерная программа DONUT нашла применение на практике [5,6].

В работе [7] указывается, что для корректировки заданного числа аберраций необходимо выполнить больше измерений интенсивности как минимум на одно.

Ещё одним способом измерения коэффициентов разложения волнового фронта по полиномам Цернике является использование многоканальных дифракционных оптических элементов, согласованных с набором базисных функций Цернике [8, 9], однако такой подход применим только для небольших аберраций [10].

После того, как аберрации оптической системы определены, выбор процедуры компенсации существующих аберраций зависит от оптической схемы и доступных для управления степеней свободы. Наиболее распространённым является управление перемещениями зеркал системы, за исключением главного. Применяется также смещение ПЗС-матрицы. Управляемые перемещения включают смещения в направлении оптической оси, смещения и наклоны в направлении перпендикулярных ей осей. Некоторые системы имеют способность упруго деформировать форму зеркала и компенсировать таким образом аберрации высокого порядка.

Для определения необходимых для компенсации аберраций смещений оптических поверхностей при- менительно к двухзеркальным телескопам существуют хорошо разработанные методы [11–15]. В работах [6, 16, 17] рассмотрены трёхзеркальные телескопы. В [18] обсуждаются вопросы аберраций и юстировки телескопов с произвольным числом зеркал.

В последнее время получили распространение методы управления положением и изменением формы оптической поверхности зеркал, основанные на компьютерном инженерном анализе. К ним относятся метод, основанный на построении матрицы чувствительности [19], и метод минимизации оценочной функции [20].

В данной статье рассматривается возможность управления не только перемещениями зеркал, но и температурным полем телескопа космического базирования. В соответствии с предлагаемой методикой выполняется расчёт ФРТ по интенсивности для набора параметров температурного поля и управляемых положений зеркал. При этом с помощью процедуры оптимизации определяется набор параметров, для которого среднеквадратическое отклонение расчётной ФРТ от измеренной минимально.

Определение расчётной ФРТ для каждого набора параметров температурного поля и положения зеркал включает в себя следующие этапы:

• -    расчёт линейных и угловых перемещений зеркал, вызванных изменением температурного поля;

• -    добавление к температурным перемещениям регулируемых перемещений;

• -    расчёт аберраций оптической системы, соответствующих суммарным смещениям зеркал;

• -    расчёт ФРТ в соответствии с полученными аберрациями.

1.    Вычисление температурных перемещений элементов оптического тракта

Рассмотрим сначала аппроксимацию приращений температурного поля конструкции телескопа в декартовой системе координат линейной функцией

T – T 00 = T 0 + T i x i ; i = 1, 2, 3, (1) где x_i – координаты декартовой системы, T ₀₀ – текущее температурное поле телескопа, T ₀, T_i – константы. По повторяющимся индексам здесь осуществляется суммирование.

В [21] показано, что постановка задачи термоупругости в перемещениях сводится как при статически определимых, так и при статически неопределимых условиях закрепления конструкции к постановке задачи изотермической теории упругости, если рассматривать в качестве дополнительного вектора объёмной силы величину (3 X + 2 ц ) а ( T - T 00 ), i , а к заданным внешним поверхностным силам добавить (3 Х + 2 ц ) а ( T - T ₀₀), i v i , где X , ц - коэффициенты Ламе, v_i – компоненты единичного вектора-нормали к поверхности, а - коэффициент температурного линейного расширения.

Поскольку в данной статье рассматриваются условия, в которых поверхностные и объёмные силовые воздействия на конструкцию телескопа отсутствуют, то с учётом (1) разности перемещений и поворотов любых рассматриваемых точек конструкции представляют собой линейные функции от четырёх констант: Tr (r = 0, 1, 2, 3). Для конструкций сложной формы эти функции могут быть получены только численно.

Изложенное позволяет записать йs = MrsTr, r = 0,1,2,3; s = 1,..., N,                  (2)

где u ɶ _s – линейные и угловые перемещения точек конструкции, вызванные температурным полем; N – общее количество рассматриваемых перемещений, M_rs – матрица влияния параметров T_r на перемещения.

В качестве примера рассматривался внеосевой четырёхзеркальный объектив. Моделирование выполнялось для 80 расчётных случаев, охватывающих различные сочетания температурных констант. Все перемещения рассматривались по отношению к положению центра ПЗС-матрицы. Поворот вокруг оптической оси не учитывался в силу осевой симметрии оптических поверхностей. Для решения использовалась программа ANSYS.

Полученная в результате аппроксимации результатов моделирования матрица является матрицей перехода от четырёх параметров температурного поля T ₀, T ₁, T ₂, T ₃ к перемещениям зеркал.

• 2.    Вычисление аберраций оптической системы, вызванных перемещениями элементов оптического тракта

Определение искажений волнового фронта в оптической системе и оценка качества изображения при проектировании выполняются с помощью программных пакетов Zemax, CodeV, OSLO, TracePro и других. Однако в случае, когда необходимо выполнить вычисления для очень большого числа вариантов смещений оптических элементов, как это требуется в соответствии с рассматриваемой здесь методикой, целесообразно использовать приближённые вычисления. Использовался приближённый метод расчёта искажений волнового фронта в оптической системе, вызванных смещением поверхностей оптических элементов как жёсткого целого, основанный на создании матрицы чувствительности волнового фронта.

Кроме перемещений, вызванных температурным полем, на оптические характеристики влияют управляемые перемещения зеркал. Представим их в виде вектора us , s= 1, ..., N, где все неуправляемые компоненты равны нулю. Полные перемещения оптических поверхностей можно записать в виде us = йs + us.                                           (3)

В соответствии с изложенным представим коэффициенты полиномов Цернике оптической системы в виде

Z k = N ks u s + Z°_k, k = 1,..., L ; s = 1,..., N ,            (4)

где Z_k ⁰ – коэффициенты полиномов Цернике оптической системы для недеформированной конструкции,

L – общее число рассматриваемых полиномов, N_ks – матрица чувствительности.

Для определения компонент матрицы чувствительности сначала выполняли серию расчётов в пакете Zemax. В них задавали смещения поверхностей зеркал и определяли коэффициенты полиномов Цер-нике, описывающих искажения волнового фронта оптической системы для отдельных комбинаций смещений. Полученные результаты аппроксимировали линейной зависимостью по методу наименьших квадратов. Таким образом, принимается, что аберрации волнового фронта могут быть описаны полиномами Цернике и что поведение системы в рассматриваемом диапазоне смещений зеркал линейно. Такой метод тем более точен, чем ближе оптическая система приближается к дифракционному пределу.

Рассматривались смещения оптической поверхности зеркал как жёсткого целого в предположении, что эксцентриситеты отсутствуют. Для описания этих смещений достаточно использовать первые три полинома стандартного ряда Цернике: константа и два наклона. Поскольку в рассматриваемой оптической системе четыре зеркала, то в (4) N = 12. Матрицы чувствительности N_ks были получены для семи точек фокальной плоскости.

Погрешность линейной аппроксимации оценивали отношением среднеквадратического отклонения значений коэффициентов полиномов Цернике оптической системы, полученных линейной аппроксимацией, от их значений, полученных оптическим моделированием в Zemax, к среднеквадратическому значению коэффициентов, посчитанных в Zemax. Соответствующие результаты для комы X в качестве примера приводятся на рис. 1. Для аберраций третьего порядка погрешность аппроксимации не превысила 0,09.

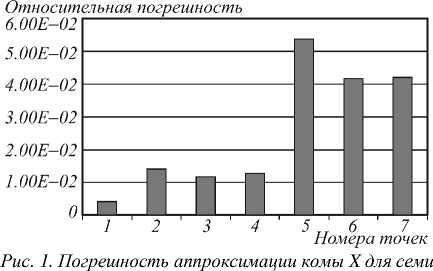
точек фокальной плоскости. Номер центральной точки – 2

3.    Численное определение функции рассеяния точки по аберрациям выходного пучка света

Интенсивность спектра вычислялась как преобразование Фурье от аберрированной функции зрачка g ( x,y ). Характеристики функции зрачка, значения аберраций и параметры оптической системы были взяты для указанной выше оптической системы, реализованной в Zemax. Преобразование Фурье имеет вид:

где f - фокусное расстояние, k = 2 л / Х , X - длина волны (0,00061 мм), a - область задания поля.

• 4.    Примеры определения характеристик температурного поля ОЭТК и управляемого перемещения вторичного зеркала, соответствующих вариации измеренной функции рассеяния точки

5.    Минимизация температурных градиентов

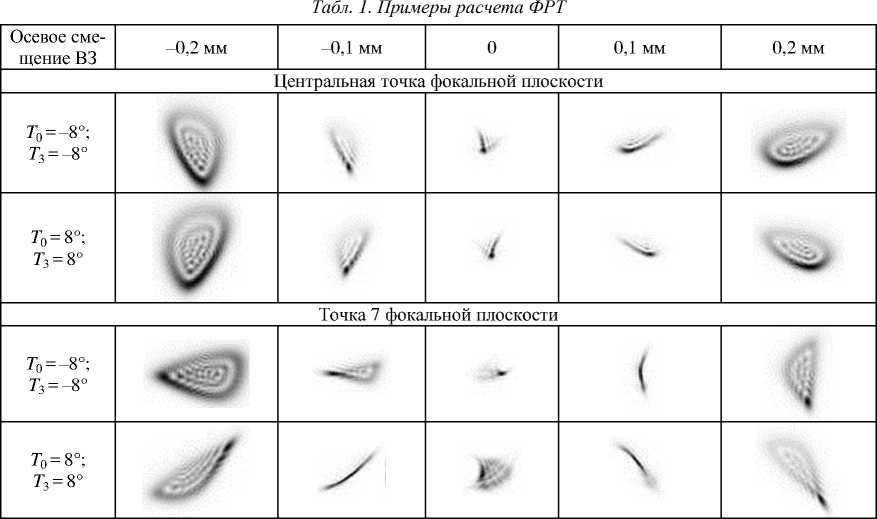
Изложенный выше алгоритм был реализован в программе Tabulator, предназначенной для определения управляющих параметров: T ₀, T ₁, T ₂, T ₃ и управляемого осевого перемещения вторичного зеркала по заданной ФРТ. Иллюстрация результатов расчётов ФРТ при T 1 = T 2 =0 и разных значениях T 0 , T 3 и осевых положений вторичного зеркала приводится в табл. 1.

На рис. 2 приводится сравнение двух разных экспериментальных ФРТ (дифракционный предел ориентировочно равен 9 мкм) с полученным расчётом по принятому алгоритму. В соответствии с ним сначала ФРТ вычислялись для наборов дискретных значений управляющих параметров – выбиралось по 10 значений каждого параметра с равномерным шагом в пределах заданных диапазонов их изменения и перебирались все возможные сочетания. Такой большой объём вычислений был реализован с привлечением кластера «Келдыш» (МГУ). Затем выбиралось наиболее близкое к измеренному расчётное значение ФРТ. Соответствующие параметры принимаются за исходные для процедуры оптимизации, в соответствии с которой определяется окончательный набор параметров, наиболее точно аппроксимирующих измеренную ФРТ. Сопоставление измеренных и расчётных ФРТ выполняется по величине среднеквадратического отклонения по всем пикселям (размером 6 мкм, рис. 2).

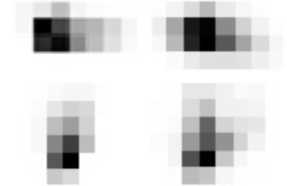
Рис. 2. Сопоставление экспериментально замеренных (слева) и расчётных (справа) ФРТ для двух рассмотренных случаев: (а) и (б). Размер пикселя – 6 мкм

Непосредственное влияние на аберрации оптической системы оказывают полные смещения оптических поверхностей зеркал. Поэтому после того, как определены полные смещения, дающие наиболее близкие к замеренным значения функции рассеяния, может быть рассмотрен вопрос о возможном уменьшении величин температурных градиентов. С этой целью при неизменных величинах полных смещений можно изменить составляющие их в соответствии с равенством (3) слагаемые. Из (3) и (4) можно получить

G ( u , v ) = ^If # ( x , У )exP - k ( xu + yv ) d x ^d У , (5) ^{2 n f}             L ^f J

a

T = M * ( u_s - u_s ) ,

где M_r ^* _s – матрица, полученная обращением или псевдообращением матрицы M rs .

Определим u _s так, чтобы компоненты вектора T r были минимальны. Для этого введём квадратичную форму

T T ₀ 2 + T 2 + T + T ₃ 2 .                          (7)

Подставляя в (7) равенства (6), нетрудно убедиться, что условия экстремума функции Ψ dT/d us = 0                                    (8)

имеют вид

M r MJ- = MX». , r = 0,1,2,3; s, t = 1,..., N. (9)

Если регулируется только одно перемещение одного из зеркал, например, осевое перемещение вторичного зеркала u ₁ , то из (9) получаем

U 1 = M * M^ t I M * M^.                     (10)

Данный экстремум является минимумом, так как сумма квадратов Mr1Mrt положительна и d2T/du12 > 0 .

Если регулируются два перемещения, например, u ₁ и u ₂ , то из (9) получаем следующие условия экстремума

M ri M> t = M *1 ( M ri U i + M *2 u 2 ) , M r2 M> t = M r2 ( M ri U i + M r2 u 2 ) .

Строгое условие того, что это минимум, имеет вид ( M ri M ri )( M *2 M r2 ) - ( M *1 M *2 ) 2 >  0.           (13)

Используя условия минимума функции многих переменных, нетрудно получить соответствующие зависимости для трёх и более управляемых перемещений зеркал.

При наличии специальных требований к управлению температурным полем слагаемые в (7) могут быть введены с соответствующими весовыми коэффициентами.

Заключение

Изложенная выше методика относится к технологии активной оптики, позволившей в течение последних двух десятилетий существенно повысить разрешающую способность наземных телескопов и телескопов космического базирования. В данной методике рассматривается возможность управления деформациями несущей конструкции наряду с управлением смещениями зеркал.

Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований и Правительства Самарской области, Проект № 16-41-630542.