Компенсация реактивной мощности в распределительных сетях горных предприятий

Горные предприятия, в особенности горнообогатительные комбинаты, характеризуются большой установленной мощностью потребителей, сложной и разветвленной структурой электрических сетей, характерным режимом работы, а также некоторыми специфическими особенностями взаимодействия с энергосистемами. В связи с этим вопросы КРМ и определение рационального местоположения компенсирующих устройств для таких предприятий приобретает весьма актуальное значение в свете энергосберегающей политики. Особенно важна компенсация при оптимизации режимов напряжения и электропотребления в целях снижения активных потерь и повышения качества электроэнергии. Эффективным мероприятием по снижению потерь в электрических сетях является установка в них устройств КРМ [1]. При переходе на энергосберегающий путь развития и с учетом роста цен на электроэнергию данная проблема приобретает еще большую актуальность.

Анализ существующих методов расчета оптимальной мощности и определение местоположения компенсирующих устройств показали, что наиболее приемлемым для горных предприятий является метод дискретного программирования (ДП) решения задачи оптимальной компенсации реактивной нагрузки (КРН), позволяющий построить модель КРН с учетом специфики электрических сетей горных предприятий (разделение на подземные и поверхностные сети), а также получить простые и эффективные     алгоритмы     решения задачи [2, 4].

Номинальную             мощность компенсирующих устройств QH (для сетей напряжением до и выше 1 кВ) и реактивную мощность, генерируемую синхронными электродвигателями (СД), можно определить целевой функцией на основе минимума приведенных затрат: N

З = £З ki Q ki + Зэ              (1)

где Зи Qki    - капитальные затраты, связанные с установкой конденсаторной установки (КУ) мощностью Qki; N -количество компенсирующих устройств (СД и КУ); Зэ- функция затрат на компенсацию реактивной мощности.

Функцию затрат Зэ удобно представить в виде

Зэ=сЛРМ,= ^| |Q-Qk№~Q-ll где c - удельная стоимость потерь мощности и энергии, приведенная к стоимости потерь активной мощности; PPM - потери активной мощности; U - напряжение сети; Q - вектор расчетных    максимальных    реактивных нагрузок узлов сети; Qk - вектор мощностей компенсирующих устройств; R - матрица узловых активных сопротивлений сети напряжением 6–10 кВ относительно главной понизительной подстанции (ГПП).

Целевая функция (1) рассматривается при ограничениях:

N

У,Q«=Q k ,  Q k......i^ Q^Q k    i = 1,2,...,N

Q k^ Q _kn       i = 1,2,..., n ,

Функцию затрат на компенсирующие устройства Зki Qki   целесообразно, в силу специфики подземных и поверхностных сетей, представить отдельно для сетей напряжением до и выше 1 кВ:

• • i -й нагрузочный узел напряжением до

1 кВ:

• ³ ki ^Q ki e^e |^³ НКБ ^Q ki ^{+ 3} ТП , ^Q ki ] ^{+ C} oPн ^Q ki

• • i -й нагрузочный узел напряжением 610 кВ:

3ki Qki = e3ВКБ Qki + СоРвQki, где e - ежегодные отчисления от капитальных затрат, включая нормативный коэффициент; 3НКБ Qfa     - затраты на низковольтные батареи; 3ТП( Qki  - снижение затрат на i -ю трансформаторную подстанцию (ТП) при установке КУ напряжением до 1 кВ мощностью Q^;;  3ВКБ Qki   - затраты на высоковольтные батареи; рн,рв - удельные потери активной мощности в КУ напряжением до и выше 1 кВ.

Стоимость КУ напряжением до и выше 1 кВ определяется выражением:

A i

3 кб , Q ki а ЛК ОлУДК 0 ,+k уд Qk, , j 1

где  3КБ/  - затраты на конденсаторную батарею; 4, Бу - число секций ТП и число КУ в секции; K (., KOi   - стоимость коммутирующего    и    регулирующего оборудования соответственно для одной секции и одной КУ; k    - удельная стоимость КУ.

Для горных предприятий характерно питание технологических участков по одно - и двухтрансформаторной схеме в зависимости от          категории          надежности электропотребителей. Поэтому при установке КУ на стороне низшего напряжения распределительных        трансформаторов возможно снижение мощности ТП (но не их количества) на ступень стандартных мощностей. Тогда

^ЗТП ^S ном   ^ЗТП ^S ном ^{,при   Q}km   ^Qk

0                    при   Q _k   Q _km ,

^ЗТП ^Qk

где S'H0Mi - номинальная мощность ТП  Sном, на ступень ниже установленной мощности i -й

ТП S . ; З_тп S ■ , 3_ 5" . — стоимость ном ,  ^; ТП ном ,  , ТП ном

ТП соответственно мощностью S и S . ном      ном

Максимальную и минимальную мощности КУ, в пределах которых возможно снижение установленной мощности ТП, можно определить по формулам:

Q k min

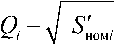
- P ²;

Q k max

^{Q     S} ном ^{2   P 2.}

Функция затрат 3ki Qki для группы однотипных СД определяется выражением

^З k ^Q k   ^eKp^m

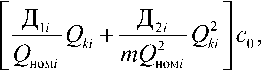
где K - стоимость регулятора возбуждения СД; m = N-n - количество СД в группе; Д,_t,

Д21. - постоянные величины, определяемые номинальными параметрами двигателя [3].

Потери активной мощности можно представить в виде

N 1

PМP0       aiQk2i  biQki где

N 1      N

⁺ 772“ S ^Qki     a kj b ij ,   ⁽²⁾

U i 1 ji 1

PP0 = 1-Q QRQ; a и b - коэффициенты, связанные с установкой и монтажем КУ :

a i_U ¹ ₂ R i ;

b_{i 2} QR_i   при i 1,2,..., N ;

R 1 i

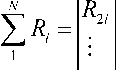
– i -й столбец матрицы N .

R Ni

Если i -ю  квадратичную функцию, стоящую в скобках, отнести к затратам на КУ в i -м нагрузочном узле Зki Qki , то функцию затрат З можно представить выражением

^N           2 c ^N 1 N

^З   c ₀ P ₀+z З _i Q_ki + 2 c ₂0 ■I Q ki I Q_kjR_ij , (3)

i 1                   U     i 1 j =z +1

где     З Q З Q+      ²

д      iki    kiki   0iki0iki функция затрат i -го нагрузочного узла или затраты, связанные с размещением в i -м узле КУ мощностью Q .

Анализ целевой функции (2) показывает, что при R 0 для всех  i1,2,...,N1 и ji+ 1,i + 2,..., N      она      сепарабельна

(separability of funkcion), т.е.

NN

З   c 0 P 0 +zЗ _i Q_ki     при  X Q ki   Q k , (4)

i 1 i 1

и задачу без затруднений можно решить методами дискретного программирования (ДП) [5, 6].

Однако условию R 0 удовлетворяют только радиальные сети, что ограничивает возможность применения алгоритмов ДП для произвольной разомкнутой сети в его классической постановке.

Несепарабельность целевой функции КРН преодолевается путем многократного уточнения режима электропотребления в сети в ходе расчета и определения дополнительных потерь мощности на общих ветвях схемы от двух переменных нагрузок. Вместе с тем многократного уточнения режимов можно избежать, приведя целевую функцию (4) к детерминированному виду.

Принимая     нумерацию     узлов упорядоченной с конца магистрали и учитывая свойства матрицы узловых сопротивлений,     получаем     последнее слагаемое целевой функции (3) в виде

N 1 N

^{2 c} 2^{0     Q}ki    ^Qkj^Rij   ^{2 c} 2^{0 Q}k 1 ^Qk 2 ^R 2+ Q k 1 + ^Qk 2 ^Qk 3 ^R 3 + ..

U i 1     ji 1           U

i 1       ji +1

где      R ₂    R ₁₂ ,      R ₃    ^R 13    ^R 23

R N    R 1 N    R 2 N        R N 1, N .

Обозначим суммарную мощность КУ, расположенных в i -м нагрузочном узле через

z

Qi    Q после соответствующей замены j1

выражение (3) примет вид

N

ЗЗ i Q k 1

i 1

Q_k ¹

₂   Q_k Q_ki

Для удобства вычислительной процедуры выражение (5) с учетом, что Q_ki QⁱQ^{i 1} , удобнее представить в виде

N

ЗЗ i Q k ⁱ Q k ^{i 1}

i 1

2 c

+ ^{2 c} 2⁰ R 1 Q k ⁱ 1 _Qk i    _Qk i 1

при ограничениях:

Qk0  0,  QkN  Qk , i1              i1           i1

Q k min    Q k     Q k max ,

Qk min  Qi k min      k      k max .

Вычислительная процедура сводится к отысканию абсолютного минимума З* по переменным Qi , Q j при фиксированных значениях других переменных  множества

Q Qⁱ , Q ^j , от которых зависит функция З .

Выбрав значение Q^{N 1} суммарной мощностью N 1 КУ и зафиксировав его, минимизируют по всем остальным переменным Q_k ¹ , Q_k ² , Q_k^{N 2} .

После       выполнения       всех вычислительных процедур минимум функции может быть представлен в виде

*             NN 1    ^{2 c} 0     N 1   N   N 1

З min З _N Q_k  Q_{k      2} R_N Q_k   Q_k  Q_k

Э N 1

ЗN1 Qk, где QN 1 может принимать дискретные значения от QkNmi1n до QkNma1x, а

N ¹

^{З Э} N 1 ^Qk ^{N 1          З} i ^Qk ^{i    Q}k ^{i 1} + ^{2 c} ₂ ⁰ R i Q k ^{i 1} Q k ⁱ   Q k ^{i 1}

i 1                      U

Эквивалентной данная функция может быть определена в зависимости от Q ^Э :

З ^Э N 1 Q k ^Э    min З N 1 Q k ^Э Q k^{N 2}

^{2 c} 2⁰ R N 1 Q k ^{N 2} Q k ^Э Q k ^{N 2}

N 2

_{З i Qk}i   _Qki 1     2 c ₂0 _RiQki 1 _Qki   _Qki 1

• i 1                       U

Аналогичным образом получают функцию ЗЭQN 2 и т.д. Этот процесс продолжается до тех пор, пока на последнем шаге не приходят к выражению

З1Э QkЭ    З1Qk1  , где Qk1min  QkЭ  Qk1  Qk1max ; З1 Qk1  – функция затрат 1-го нагрузочного узла.

Минимизация    выполняется    для каждого фиксированного значения QЭ из интервала Qkimin;Qkimax перебором значений мощностей Qi 1 , для которых выполняется условие Qkim1in Qki 1 Qkim1ax. Переменные Qki 1 принимают дискретные значения с наперед заданным шагом квантования h .

Эквивалентная характеристика затрат ЗЭQЭ    определяет минимум затрат в магистральной электрической сети при оптимальном    размещении    источников реактивной мощности в i -х нагрузочных узлах суммарной мощностью QЭ .

Процесс построения эквивалентной характеристики З ^Э Q ^Э означает замену i -х нагрузочных узлов с источником реактивной мощности (ИРМ) в каждом мощностью Q^{i 1} эквивалентным нагрузочным узлом с ИРМ

i мощностью QЭ Qi Q , функция затрат j1

которого определяется эквивалентной характеристикой З ^Э Q ^Э .

Расчет проводится от конца магистрали ( i = 1, 2, 3,..., N ) и продолжается до тех пор, пока все нагрузочные узлы магистральной линии не эквивалентируются в один нагрузочный узел и не будет определен оптимум затрат З^Э Q З^*.

Вывод. Предложен подход к определению рационального местоположения компенсирующих устройств в распределительных сетях горных предприятий методом дискретного программирования. Этот метод позволяет найти оптимальный вариант решения задачи при наложении на целевую функцию определенных ограничений и правил.

Библиографический список 1. Железко Ю.С. Выбор мероприятий по снижению потерь электроэнергии в электрических сетях: Руководство для практических расчетов. – М.: Энергоатомиздат, 1989. - 176 с.

• 2.    Кротов В.Ф. Основы теории оптимального управления. - М.: Высш. шк., 1990. - 432 с.

• 3.    Плащанский Л.А. Основы электроснабжения горных предприятий. Учебник для высших учебных заведений. - М.: Изд-во МГГУ, 2006. - 499 с.

• 4.    Kirchmayer L.K. Economie Operation of Power Systems. Jon Welley a Suns, 1958.

• 5.    Акулич И.Л. Математическое программирование в примерах и задачах. Учебное пособие. – М.: Высш. шк., 1986. – 318 с.

• 6.    Мину М. Математическое программирование. Теория и алгоритмы/перевод с французского /. – М.: Наука, 1990. – 488 с.