Компьютерная имитация и анимация управляемого движения информационного спутника

При проектировании космических информационных систем применяются современные компьютерные технологии. Программная система SIRIUS-S разработана в отделе «Навигации, наведения и управления движением» НИИ ПНМС СамГТУ и предназначена для эскизного проектирования систем наведения, навигации и управления движением информационных спутников [1]. Данная программная система может применяться для анализа различных вариантов служебных систем космического аппарата (КА) и формирования требований к измерительным и исполнительным подсистемам бортового комплекса управления.

Программная система SIRIUS-S содержит диалоговый монитор, подсистемы моделирования, синтеза и анализа, а также технологические подсистемы анимации пространственного движения КА и документирования результатов. Управление работой SIRIUS-S выполняется с помощью системы иерархических меню. В результате инженер-разработчик получает функциональный облик системы управления проектируемого спутника радиолокационного или оптико-электронного наблюдения в отношении периодичности, производительности и оперативности, разрешения на местности, точности наведения и стабилизации КА с учетом возмущений, ограничений и др. факторов.

при длительном временном интервале полета носителя радиолокатора. При этом происходит искусственное увеличение (синтез) апертуры антенны за счет движения радиолокатора и последующей цифровой обработки измерений. Радиолокаторы с синтезированной апертурой (РСА) космического базирования в настоящее время достигли высокого технического совершенства и являются важным средством мониторинга поверхности Земли. За счет особенностей электромагнитного излучения в радиодиапазоне такие системы в меньшей степени зависят от метеорологических условий и орбитального расположения, чем их аналоги в видимом и инфракрасном диапазонах. Применение РСА с активной фазированной антенной решеткой (АФАР) существенно упрощает реализацию различных режимов радиоэлектронной съемки.

В системе SIRIUS-S реализованы модели Земли, конструкции КА, его поступательного и углового движения как при различных видах сканирующей съемки, так и при поворотных маневрах. Эти модели позволяют выполнить точный расчет всех кинематических параметров пространственного движения КА и сформировать набор xm-файлов для подсистемы визуализации. Документируемые результаты представляются сценами маршрутов съемки на картографической основе, таблицами и графиками изменения координат движений КА и исполнительных органов в функции времени, значениями достигнутых характеристик качества наблюдения и критериев оптимальности.

Подсистема моделирования содержит следующие компоненты: модель Земли и электронные карты с базами данных для объектов на земной поверхности; структурная модель КА – геометрические и инерционные характеристики конструкции, параметры телескопов и антенн, исполнительных органов, измерительных

Рис. 1. Геостационарные спутники связи: a ) Луч-5А/В ; b ) Экспресс-АМ5/6

Рис. 2. Спутники оптико-электронного землеобзора: a ) Ресурс-П ; b ) Сириус-1

подсистем и др.; баллистическая модель движения центра масс КА; модели углового движения КА – схемы обзора земной поверхности, методы расчета маршрутных движений и поворотных маневров (ПМ) с краевыми условиями общего вида и др.; модели внешней обстановки – методы расчета освещенности наблюдаемой поверхности, облачности и др.; модели приемного тракта – методы расчета скоростей движения изображения на матрицах оптико-электронных преобразователей (ОЭП) при оптической сканирующей съемке, разрешающей способности и др.; модели целевой обстановки – базы данных задач и объектов наблюдения.

Подсистема анализа и синтеза предназначена для выполнения таких функций: отображение карт земной поверхности с объектами наблюдения; отображение орбиты и трассы полета КА, полосы обзора; расчет орбитального поступательного и углового движения КА, проверка их реализуемости при ограниченных ресурсах исполнительных органов; синтез алгоритмов определения ориентации, законов наведения, цифрового и широтно-импульсного управления КА; анализ устойчивости и качества переходных процессов в системе управления ориентацией (СУО) спутника при выполнении требуе- мого движения; расчет энергобаланса системы электропитания, освещенности наблюдаемой местности, радио-видимости пунктов приема информации и др.; расчет пространственного разрешения на местности; анализ вариантов построения СУО КА по различным критериям; расчет эффективности функционирования информационного спутника по критериям периодичности, производительности и оперативности наблюдений на основе компьютерной имитации. В этой подсистеме алгоритмы имитации реализованы в среде MatLab.

Подсистема анимации пространственного движения КА является технологическим программным средством, созданным в среде Delphi 7 с применением графической библиотеки OpenGL. 3D-модель конструкции КА реализована в среде Blende, отображение ее элементов с учетом освещённости Солнцем выполняется средствами OpenGL. Здесь с использованием стандартной процедуры «наклейки» текстуры в виде карты Земли на её поверхность отмечаются объекты наблюдения, их геодезические координаты рассчитываются в системе координат (СК) текстуры и определяется положение КА в СК сцены съемочной камеры. Отображаются конструкция КА с текущей точкой трассы по- лета, точкой пересечения линии визирования с поверхностью Земли и проекцией линейки ОЭП на эту поверхности, если в этот момент выполняется съемка. Программа визуализации позволяет изменять масштаб изображения и ракурс наблюдения сцены при сканирующей съемке заданного участка на поверхности вращающейся Земли.

Программная система SIRIUS-S успешно применялась при автоматизированном проектировании многих информационных спутников, например геостационарных спутников связи Sesat , Луч-5А/В, Экспресс-АМ5/6 разработки АО «Информационные спутниковые системы им. акад. М.Ф. Решетнева» (рис. 1), спутника оптико-электронного землеобзора Ресурс-П разработки АО РКЦ «Прогресс», а также перспективного спутника Сириус-1 для оптикоэлектронного наблюдения, рис. 2.

В последнее время проявился существенный интерес предприятий космической промышленности к применению программной системы SIRIUS-S для полетного сопровождения (поддержки) систем управления движением информационных спутников. Современное представление фактической ориентации КА с помощью кватернионов создает проблему при пространственном восприятии поступающей телеметрической информации для верификации бортового расчета соответствующих законов наведения КА. Вторая проблема состоит в том, что при возникновении отказов бортовой аппаратуры управления возникает существенное отклонение фактического углового движения КА от программного движения. При этом, несмотря на доступность телеметрической информации от работоспособных измерительных приборов о фактической ориентации спутника, возникает задача квалифицированной интерпретации аномальной ориентации КА относительно направлений на Землю, на Солнце и на другие внешние ориентиры. Поэтому наличие в центре управления полетами компьютерной среды для анимации пространственного движения КА по телеметрическим данным весьма желательно.

В статье кратко представляется компьютерная среда для анимации движения информационных спутников, работа которой демонстрируется для последовательности сканирующих маршрутов, включающей маршруты стереоскопической съемки заданных участков земной поверхности.

ПРОГРАММНАЯ СРЕДА АНИМАЦИИ

На рис. 3 показан пример визуализации конструкции спутника землеобзора Sirius-1 в среде Blender. Модель конструкции этого КА представлена системой твердых тел и содержит корпус спутника, телескоп с подвижной крышкой объектива, кластер четырех реактивных двигателей-маховиков (ДМ), четыре звездных датчика системы определения углового положения (СОУП) в составе бесплатформенной инерциальной навигационной системы (БИНС), двигательную установку на основе 8 реактивных двигателей, бортовые антенны, принимающие сигналы навигационных систем ГЛОНАСС/GPS, и четыре подвижные панели солнечных батарей (СБ), каждая панель в двухстепенном кардано-вом подвесе по схеме «вилка». Предусмотрена возможность отображения перемещений элементов конструкции спутника, что достигается за счет изменения их угловых координат по степеням подвижности. Отображение пространственного положения 3D-модели спутника с учетом освещённости Солнцем выполняется средствами OpenGL. При изменении положения центра масс и ориентации КА изображение его конструкции в текущей сцене «перерисовывается», что создает эффект анимации пространственного движения спутника относительно вращающейся Земли с отображением текущего положения важнейших объектов внешней космической среды – Солнца, Луны и др.

Анимация движения КА реализуется программным средством, созданным в среде Delphi 7 с применением графической библиотеки OpenGL, т.е. на основе свободно распространяемых программ, в отличие от известной системы STK (Analytical Graphics, Inc., . Здесь

Рис. 3. Облик конструкции КА Sirius-1

программно выполняется процедура «наклейки» текстуры в виде карты Земли на её поверхность, отмечаются объекты наблюдения, рассчитываются их географические координаты и далее программно реализуется собственно 6D-анимация движения спутника.

Обработчик события OnCreate для генерации формы содержит следующие строки:

SetDCPixelFormat(Canvas. Handle); // формат пикселя hrc: = wglCreateContext(Canvas. Handle);

// контекст воспроизведения

Здесь первая строка – обращение к пользовательской процедуре procedure SetDCPixelFormat (hdc: HDC);

var pfd: TPixelFormatDescriptor; nPixelFormat: Integer;

begin

FillChar (pfd, SizeOf (pfd), 0);

nPixelFormat: = ChoosePixelFormat (hdc, @pfd);

SetPixelFormat (hdc, nPixelFormat, @ pfd);

end;

Обработка события onpaint выглядит так: wglMakeCurrent (Canvas. Handle, hrc);

// установить контекст glClearColor (0.5, 0.5, 0.75, 1.0); // цвет фона glClear (GL_COLOR_BUFFER_BIT); // очистка буфера цвета wglMakeCurrent (0, 0); // освободить контекст

procedure texture(k1,k2:integer;p:poin ter);

begin glTexParameteri(GL_TEXTURE_2D,      GL_

TEXTURE_MAG_FILTER, GL_linear);

glTexParameteri(GL_TEXTURE_2D,      GL_

TEXTURE_MIN_FILTER, GL_linear);

glTexImage2D (GL_ TEXTURE_2D,0,3,k1,k2,0,GL_RGB,GL_ UNSIGNED_BYTE,p);

glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ ENV_MODE, GL_MODULATE);

glEnable(GL_TEXTURE_2D);

end;

texture(2048,1024,tx);

tx:=readbitmap(tdir+’textures

Этой командой описывается двумерная текстура и указывается ее разрешение.

Теперь мы имеем карту земной поверхности и необходимо нанести на нее объекты информационного обслуживания, которые хранятся в массиве. Здесь следует преобразовать географические координаты объектов в координаты среды OpenGL. В рассчитанном массиве мы имеем широту и долготу объектов обслуживания, причем широта ф изменяется в интервале (- п/2,+п/2), а долгота X - в диапазоне (0, п). Условия преобразования: если X < п, то без изменений, иначе X:=X- 2п. Формулы преобразования x = X / п и у = ф /(2п)реализованы в упрощенном коде программы glpointsize(2); // размер точек(2)

for i:=1 to num do begin // цикл рисования glcolor3f(1,0,0); // цвет точек (красный) glbegin(gl_points);

if lm[i]<=180 then glvertex3f(lm[i]/180,0.5* fi[i]/90,1.001)

else glvertex3f(-1+(lm[i]/-180)/180, 0.5* fi[i]/90,1.001);

glend;

end;

Представленный код отличается от оригинального кода программы в среде OpenGL . Это сделано для того, чтобы не акцентировать внимание на условия и способ извлечения координат из массивов записей. Между командами glbegin(gl_points) и glend располагается код рисования c использованием описанной процедуры пересчета координат, где lm[i] и fi[i] – массивы значений долготы и широты соответственно, а num – длина массива. Для изменения масштаба используется команда glScalef с 3 аргументами в виде масштабных множителей для каждой оси.

Имитация движения КА землеобзора с цифровой системой управления выполнена в программной системе SIRIUS-S с применением среды Matlab . С использованием среды Blender отображаются конструкция КА, текущая точка трассы КА, точка пересечения линии визирования бортового телескопа с поверхностью Земли и проекция центральной линии матрицы ОЭП на эту поверхность, если в этот момент выполняется сканирующая съемка.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Стандартным образом вводятся инерциальная (ИСК) и геодезическая Гринвичская (ГСК) системы координат с началом центре Земли О _@ , орбитальная (ОСК) и связанная с корпусом спутника (ССК) системы координат с началом в его центре масс O . Ориентация ССК в ИСК определяется кватернионом Л = ( X₀, X ) , где X = { X i } , а в ОСК - углами Крылова ф i в последовательности 312.

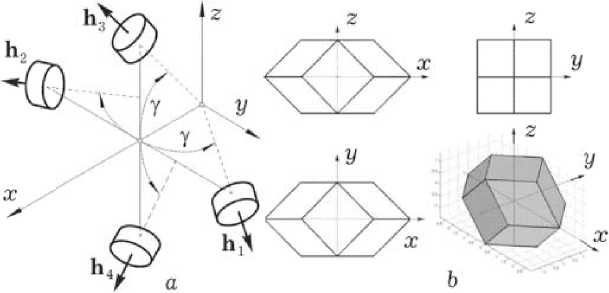
Рис. 4. Схема GE ( a ) и оболочка ее КМ ( b )

Схема General Electric ( GE ) кластера ДМ, рис. 4, обладает возможностью управлять ориентацией КА при отказе любого одного маховика. Здесь в ССК O xyz оси вращения четырёх ДМ располагаются на поверхности конуса с углом полу-раствора у . Далее используются стандартные обозначения col( - ) = { • } , lineQ = [ • ] , ( • ) * , (J , [ a x ] и ° ,~ для векторов, матриц и кватернионов, C _y = cos у , S _y = sin y , i = 1,2,3 = 1 ^ 3 , применяется вектор модифицированных параметров Родрига (МПР) G = { о i } = е tg( Ф /4) с традиционными обозначениями орта Эйлера e и угла Ф собственного поворота, который взаимнооднозначно связан с кватернионом Л ориентации КА в ИСК прямыми G = X / (1 + X ₀) и обратными X ₀ = (1 — о ²)/(1 + о ²) , Х = 2 g /(1 + о ²) соотношениями. Модель углового движения КА учитывает упругость его конструкции и имеет вид [2] -[4].

Л = Л ° o/2 ; A o { o , q , Q } = { F “ , F ^q, F ^Q } , (1) где F “ =— [ o x ] G + M ^m + M ^d ;

F ^q = - a q ( V q q + W _q q ) ; F ⁿ = M - M ^f ;

A °

J   D q   J r A Y

D‘   A ^q 0

q

J r A Y    0    J r 1 4

A y

C y S y 0

C y

C y

C y

S y

-

S y

Здесь G = G ^o + D _q q является вектором кинетического момента (КМ) системы, где G ° = К + Н и K = J o , столбцы Н = { H i } и h = { h p = J r Q p } , p = 1 ^ 4 , представляют КМ кластера и отдельных ДМ, которые связаны соотношением Н = A _y h , где матрица A _y составлена из ортов осей вращения ДМ в ССК; A ^q = diag{ j V _е = diag{|Q S }; W q = diag{( Q _Y -)²}; M ^m = { m “ }; M = { m_p };

M ^f = { m p }; вектор механического момента МП M ^m = { m™} = — L x B [6], где вектор электромагнитного момента (ЭММ) L = {l i } с ограниченными компонентами | l i | <  l^m и вектор индукции магнитного поля Земли B = b B с ортом b определены в ССК; векторы-столбцы M = { m_p } и M ^f = { m p } представляют управляющие моменты и моменты сил сухого трения по осям вращения ДМ, а вектор M ^d - внешние возмущающие моменты. Ресурсы каждого ДМ по управляющему и кинетическому моментам ограничены согласно соотношениям | m p ( t )| < m^m,| h p ( t ) < h^m , p = 1 ^ 4 .

Вектор M ^r управляющего момента кластера ДМ формируется в виде M ^г = — Н , где ( • ) - символ локальной производной по времени. Если корпус КА считать твердым телом, то G = G ^o и модель динамики его углового движения принимает вид

J o + [ ox ] G ^o = M ^r + M ^m + M ^d .    (2)

Если задано программное угловое движение КА Л ^p ( t ), О ^p ( t ), О ^p ( t ) = E ^p ( t ) (закон наведения) в ИСК, то погрешность ориентации определяется кватернионом Е = ( e ₀ , е ) = Л ^p ° Л , вектором Эйлера Е = {е ₀ , е } , где вектор e = {e i } , матрицей С ^е( Е ) = 1 ₃ — 2[ e x ] Q e , где Q _e = I ₃ e ₀ + [ e x ] , и вектором 8 ф = {8ф i } = { 2 e ₀ e i } , а погрешность стабилизации угловой скорости 8 0 = { 8о i } = о — С ^е о ^p ( t ) .

Пусть дискретное измерение кватерниона ориентации Л m = Л ^m ( t, ) КА с помощью СОУП выполняется с периодом T_p , где Л m ( t l ) = Л ( t, ) ° Л ” , кватернион Л n = Л ⁿ ( t l ) представляет центрированный гауссовский шум, t, + 1 = t, + T p , l e N o ^ [0,1,2,3...) , а дискретное измерение угловых скоростей вращения ДМ Q _ps =Q _p ( t_s ) - в моменты времени t s с периодом T_q , t s + 1 = t s + T q , s e N ₀ . Будем считать, что в моменты времени t k с периодом T u , t k ₊ i = t k + T u , k e N ₀ , формируется цифро-

вое управление ДМ, а в моменты времени t_r с периодом T m >  T u , t r + i = t r + T u ^m, r e N _o ^-цифровое управление МП, когда значения компонентов вектора ЭММ L = {l i } фиксируются ^V t ^{e [} t r , t r + 1 ) .

При балансе СУО по вектору КМ с условием G ^o = 0 и отсутствии внешних моментов ( M ^m = 0 , M ^d = 0 ) модель (2) динамики углового движения КА принимает вид О = е с вектором углового ускорения е = J 1 M ^r , а модель углового движения КА – простое кинематическое представление

Л = Л ° о /2; (Ь = е ; е = е * = v .    (3)

Модули векторов to ( t ) , е ( t ) и е * ( t ) ограничены, | о ( t )| <го , | е ( t )| <е и | е * ( t )| <8 * , что обусловлено ограниченностью областей вариации векторов КМ H и управляющего момента M ^r = - H * кластера ДМ, а также допустимым темпом его изменения. Разработанный [4] аналитический метод синтеза закона наведения КА при пространственном ПМ спутника на интервале времени t e [ t i p , t f ] с краевыми условиями общего вида

Л ( t? ) = Л _{i; Ю} ( t , ’ ) = ю _i; e ( t i ' ) = e , ;

Л ( t ? ) = Л _f ; ю ( t ? ) = ю _f ; e ( t ? ) = e _f ; e ( t ? ) = e _f основывается на необходимом и достаточном условии разрешимости классической задачи Дарбу. Здесь решение представляется как результат сложения трех одновременно происходящих элементарных поворотов «вложенных» базисов E _k вокруг ортов e _k , k = 1 ^ 3 осей Эйлера, положение которых определяется условиями (4).

Для кластера ДМ принципиальная проблема заключается в распределении векторов его кинетического H и управляющего M ^r = - H * моментов между четырьмя ДМ. Для решения этой проблемы используется скалярная функция настройки, которая обеспечивает однозначное распределение векторов H и M ^r по явным аналитическим соотношениям.

В СУО применяются дискретная рекуррентная фильтрация сигналов СОУП с периодом Tp , цифровой закон управления кластером ДМ с периодом Tu , компенсационная схема разгрузки от накопленного КМ с помощью цифрового управления МП с периодом Tum и компенсация f влияния моментов сил сухого трения mp по осям вращения ДМ с использованием дискретного наблюдателя Луенбергера. Здесь выполняется фильтрация значений вектора углового рассогласования е l = -5фl = -2e0lеl, l e No, с периодом Tp и формируются значения вектора рассогласования е k , к g N0, которые использу ются в законе управления кластером ДМ g к+1 = Bg к + с е k; й к = Kg к + р е f;

М' = юк х G: + J(c: e p + [с: ю p х]ю4 + mJ,() к       к       к          к к        к к      к       к где С: = Се(Е,) и G° = Jю^+ Н,.

k     k    k kk

ЗАКОНЫ НАВЕДЕНИЕ ПРИ СТЕРЕОСКОПИЧЕСКОЙ СЪЕМКЕ

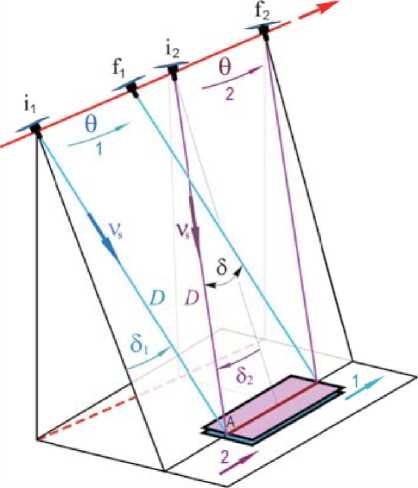
Рис. 5. Схема стереосъемки

На рис. 5 приведена упрощенная схема стереоскопической съемки, которая содержит два маршрута сканирования заданного участка земной поверхности, причем для иллюстрации идеи эта поверхность считается неподвижной плоскостью. Здесь красной прямой линией отмечена орбита спутника с начальными (initial) i j и конечными (final) f j точками первого (j = 1, голубой цвет) и второго (j = 2, бордовый цвет) маршрутов, красная пунктирная прямая линия представляет след орбиты. Если для наглядности описания стереосъемки с углом конвергенции 8 использовать стандартные понятия для направлений векторов в ОСК, то каждый маршрут сканирования начинается в фиксированной точке A в ГСК, заданной с превышением относительно поверхности общеземного эллипсоида. При этом в момент времени 11(1) начала первого маршрута с дальностью D наблюдения точки A орт целеуказания v s получается отклонением от надира сначала по крену и затем по тангажу на угол 81 = 8/2. Первый стерео маршрут съемки должен выполняться с условиями D = const, 81= const Vt e [ti1), tf1)] за счет углового наведения КА в ОСК по углу тангажа θ , см. рис. 5, голубой цвет. Далее следует поворотный маневр КА на интервале времени t g [tf1), ti(2)]. В момент времени ti® начала второго стерео маршрута съемки с той же дальностью D наблюдения указанной точки A в ГСК орт целеуказания ν формируется отклонени-(2)

ем от надира, достигнутого при t = t i , по крену и тангажу на угол δ₂ = -δ/2 . Этот маршрут должен выполняться с условиями D = const , 5 2 = const V t g [ t i® , t f²⁾ ] также за счет углового наведения КА в ОСК по углу тангажа θ , см. рис. 5, бордовый цвет.

При синтезе закона наведения КА для получения стереопары изображений заданного участка в полной модели земной поверхности на маршрутах сканирования с двумя ракурсами следует учитывать, что невозможно обеспечить строгое постоянство продольной скорости движения изображения (СДИ) в центре матрицы ОЭП при соблюдении основного условия D = const стереосъемки. Здесь приходится изменять текущие значения азимута A маршрута и продольной СДИ в центре матрицы ОЭП. Начало A первого стерео маршрута съемки (МС1) определяется из условия достижения значения угла δ1 = δ/2 между траверсом точки A на орбитальное положение КА и ортом целеуказания νs на эту точку при заданном угле конвергенции δ . Это условие определяет также момент времени ti(1) начала МС1 и дальность Di(1) наблюдения точки A. Выполняется расчет закона углового наведения КА, движущегося по известной орбите, при итерационной вариации значений азимута A маршрута и значения продольной СДИ так, чтобы в результате выполнения такого шага дальность D наблюдения достигнутой точки на земном эллипсоиде была равна D(1) = D. Далее описанная процедура повторяется с периодом Ts в очередной достигнутой точке МС1 и процесс численного построения закона углового наведения КА на первом маршруте съемки завершается по превышению заданной длины МС1 на земном эллипсоиде. Момент времени t(2) начала второго стерео маршрута съемки (МС2) определяется из условия достижения дальности D наблюдения точки A при угле δ2 = -δ/2 между траверсом этой точки на КА и ортом целеуказания νs на точку A. Для совпадения МС1 и МС2 на земном эллипсоиде шаги построения закона углового наведения КА на втором маршруте выполняются также с периодом Ts , но в классе ортодро-мической съемки с обеспечением постоянства дальности наблюдения D при азимуте A(t®) и совпадения следа оси визирования телескопа на земном эллипсоиде с центральной линией МС1 [5].

Аналитическое представление законов углового наведения спутника в ИСК при известных численных данных для двух маршрутов сканирующей стереосъемки основывается на интерполяции этих данных векторной функцией МПР σ как векторного сплайна седьмого порядка с 8 трехмерными столбцами коэффициентов, которые вычисляются на основе с помощью аналитических соотношений. Краевые условия для поворотного маневра КА между этими маршрутами стереосъемки рассчитываются также на основе явных аналитических соотношений.

Законы наведения КА на солнечно-синхронной орбите (ССО) высотой 720 км для

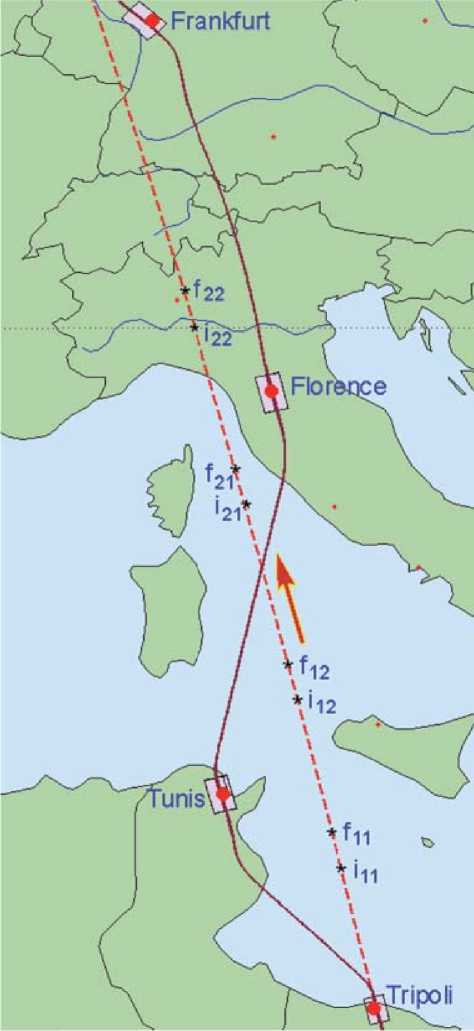
Рис. 6. Маршруты съемки на карте маршрутов съемки, в том числе стереосъемки с углом конвергенции δ = 30 град, представлены на рис. 6. Здесь при отчете времени от момента прохождения КА восходящего узла орбиты отмечены

• •    трассовая сканирующая съемка, маршрут Триполи , t ∈ [539.25, 549.25] с;

• •    ПМ маршрут Триполи ⇒ стерео МС1 Тунис , t ∈ [549.25, 580.75] с;

• •    стерео МС1 Тунис с азимутом A = - 13.42 град, точки i ₁₁ и f ₁₁, t ∈ [580.75, 591.25] с;

• •    ПМ стерео МС1 Тунис ⇒ стерео МС2 Тунис , t ∈ [591.25,647.25] с;

• •    стерео МС2 Тунис с азимутом A = - 13.42 град, точки i ₁₂ и f ₁₂ t ∈ [647.25, 658] с;

• •    ПМ стерео МС2 Тунис ⇒ стерео МС1 Флоренция , t ∈ [658, 690.75] с;

• •    стерео МС1 Флоренция с азимутом A = - 14.18 град, точки i ₂₁ и f ₂₁, t ∈ [690.75,701.5] с;

• •    ПМ стерео МС1 Флоренция ⇒ стерео МС2 Флоренция , t ∈ [701.5,756] с;

• •    стерео МС2 Флоренция с азимутом A = - 14.18 град, точки i ₂₂ и f ₂₂, t ∈ [756,766.75] с;

• •    ПМ стерео МС2 Флоренция ⇒ маршрут Франкфурт , t ∈ [766.75,810.75] с;

• •    съемка с выравниванием, марш-

• рут Франкфурт с азимутом A = -45 град, t∈[810.75,820.75] с.

На рис. 7 приведен синтезированный закон наведения спутника для выполнения маршрутов сканирующей съемки указанных видов и поворотных маневров между ними. Здесь учитывались ограничения | ω ( t ) | ≤ 1.5 град/с и | ε ( t ) | ≤ 0.2 град/с² на модули векторов угловой скорости и углового ускорения корпуса КА, обусловленные ограниченными ресурсами кластера ДМ по допустимой области вариации вектора его КМ и допустимым ускорениям ротора каждого ДМ.

Первые два набора графиков на рис. 7 представляют ориентацию ССК относительно ИСК (вектор МПР σ = { σ _i } ) и относительно ОСК (углы крена φ ₁ , синий цвет; рыскания φ ₂ , зеленый цвет и тангажа φ ₃ = θ , красный цвет).

ИМИТАЦИЯ И АНИМАЦИЯ

Имитация выполнена для спутника землеоб-зора с тензром инерции J = diag{812; 587; 910} кгм² на указанной ССО, в его модели (1) учтены упругие колебания каждой панели СБ с парциальными частотами первого тона Ω ¹ _j ≈ 0.6 р/c и декрементом δ = 0.01 . При шуме БИНС с СКО σ ^a = 1 угл. сек в процессе измерении угло-

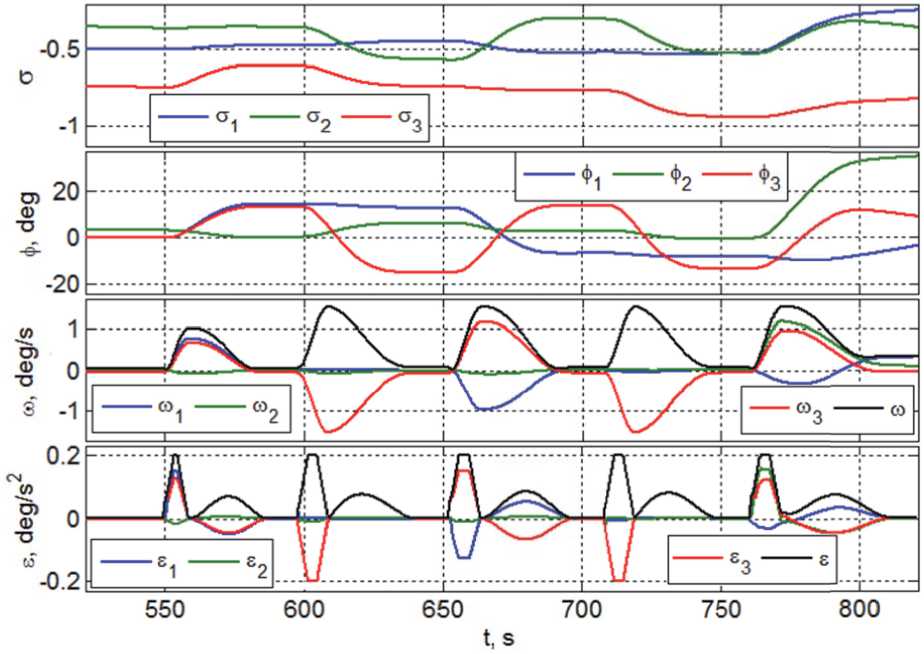
Рис. 7. Закон углового наведения КА для выполнения заданных маршрутов съемки

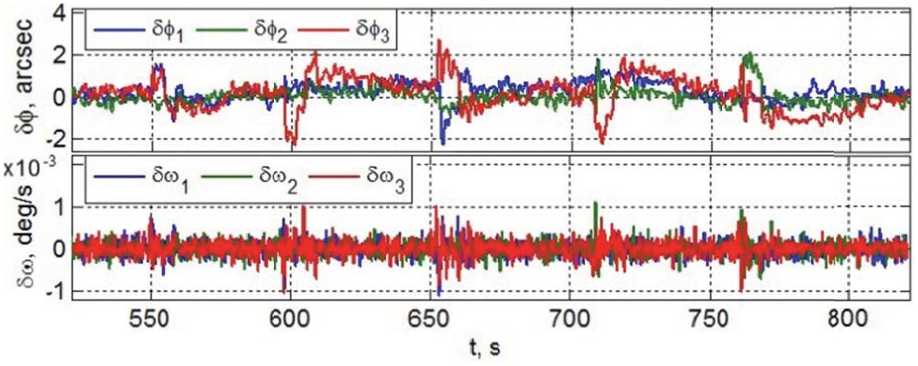
Рис. 8. Погрешности реализации закона наведения для заданных маршрутов съемки

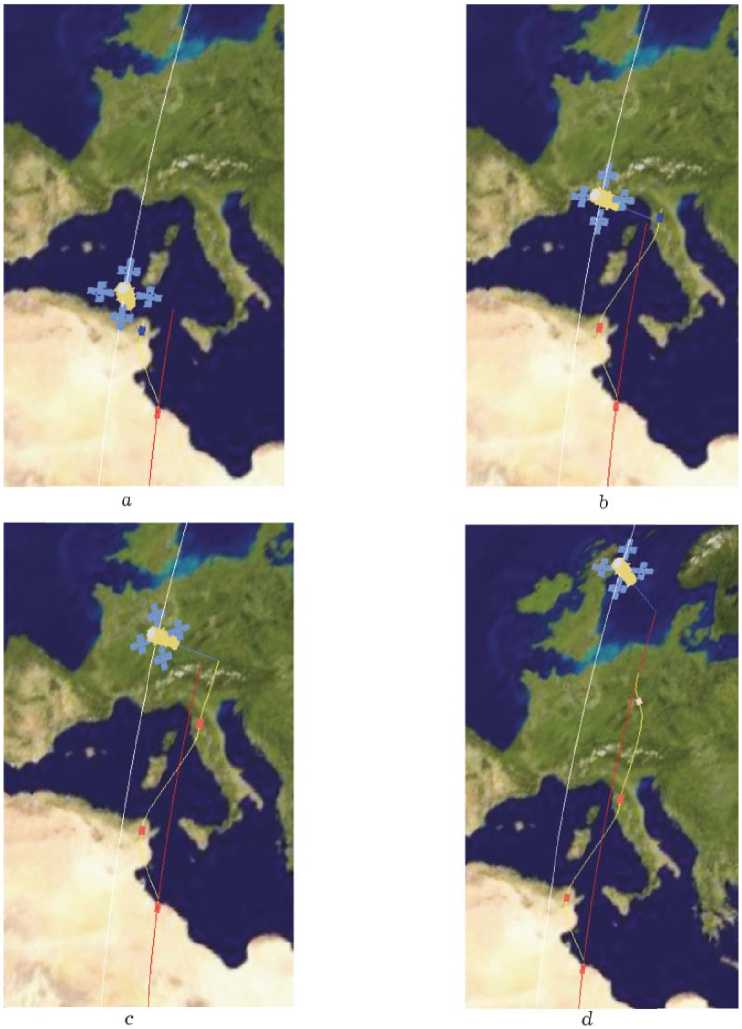
Рис. 9. Фрагменты четырех кадров анимации движения КА при выполнении задания вого положения КА в ИСК с периодом Tq = 1/ 8 с дискретная фильтрация измерений выполнялась с этим же периодом, а цифровое управление кластером ДМ формировалось по закону (5) с периодом Tu = 1/ 4 с. Погрешности по углам δφi и угловым скоростям δωi, полученные при компьютерном анализе реализации синтезированного закона углового наведения КА для выполнения заданных маршрутов съемки (см. рис. 7), представлены на рис. 8.

На рис. 9 приведены фрагменты четырех кадров анимации движения КА при выполнении указанного задания:

• a )    трассовая сканирующая съемка в надир, маршрут Триполи , ПМ, первый стерео МС1 Тунис ;

• b )    продолжение, ПМ, второй стерео МС2 Тунис , ПМ, первый стерео МС1 Флоренция;

• c )    продолжение, ПМ, второй стерео МС2 Флоренция , поворотный маневр;

• d )    продолжение, съемка с выравниванием, маршрут Франкфурт , поворотный маневр.

Нетрудно убедиться, что только результаты анимации на рис. 9 позволяют интерпретировать (зрительно воспринять и объяснить) изменение ориентации спутника в процессе его пространственного движения, определенного законом углового наведения при выполнении заданных маршрутов съемки (рис. 7) с учетом орбитального движения центра масс космического аппарата.

ЗАКЛЮЧЕНИЕ

Кратко представлена разработанная компьютерная среда для анимации движения информационных спутников и продемонстрирована ее работа для последовательности сканирующих маршрутов оптико-электронной съемки, включающей маршруты стереоскопической съемки заданных участков земной поверхности. Приведены результаты компьютерной имитации динамических процессов при угловом движении спутника землеобзора, управляемого минимально-избыточным кластером реактивных маховиков по сигналам астроинерциальной системы определения углового положения, в процессе реализации закона углового наведения КА, который синтезирован для выполнения заданных маршрутов сканирующей съемки.