Компьютерная конечно-элементная модель взаимодействия утка с основными нитями в процессе прибоя на ткацком станке

Процесс прибоя уточной нити к опушке ткани и формирования нового элемента ткани настолько важен, что, несмотря на огромное количество исследований, тема по-прежнему остается актуальной, и новую информацию получают с применением все более современных, ранее недоступных методов. Один из последних полных обзоров на эту тему сделал Б.М. Примаченко [1]. Отметим, что при всем обилии работ динамика деформации нитей в области их взаимодействия при прибое не рассматривалась, поскольку все модели основывались на конечномерных или одномерных моделях.

Во многих тканях технического назначения в качестве основы и утка применяют не пряжу, а мононити. В этих случаях специфическая структура пряжи, обусловленная большим числом образующих ее волокон, не оказывает своего влияния на взаимодействие нитей в процессе формирования элемента ткани [2]. Поэтому для анализа взаимодействия можно использовать методы механики деформируемых сплошных сред, в частности, метод конечных элементов (МКЭ) [3, 4]. Компьютерное моделирование с применением МКЭ позволяет получить детальную информацию о динамике воздействия утка на основные нити во время прибоя и обратной реакции нитей основы на уток, сжатие его поперечного сечения [5‒7].

Поскольку прибой уточной нити осуществляется сразу по всей ширине станка, уточная нить взаимодействует одновременно со всеми основными нитями в заправке, количество которых исчисляется сотнями и тысячами. Это обстоятельство позволяет рассматривать два варианта усредненной по нитям основы геометрической модели (рис. 1).

В них раскрытый зев нитей основы представлен крестообразной фигурой. Уточная нить под действием зубьев берда прижимается к нитям основы и вдавливается в створ зева. Считать воздействие берда на уток ударом вряд ли правомерно, поскольку ни в одной из моделей не учитываются масса и инерция утка. На наш взгляд, правильнее рассматривать принудительное перемещение утка под действием берда. Деформация как утка, так и основы происходит вследствие такого перемещения, которое передается через уток основным нитям, и определяется взаимодействием этих трех составляющих процесса прибоя «бердо – уточная нить – система основных нитей». Разумеется, на результат – строение сформированного элемента ткани – влияют натяжения в системе упругой заправки нитей и ранее заработанные в полотно уточные нити, но в нашем случае эти факторы не включены в модель.

Если у материала уточной нити достаточно высокий модуль упругости, то нить сохраняет форму круга (на рисунке 1 геометрическая модель слева, вариант 1). Если же материал уточной нити сжимается под действием сил со стороны берда и нитей основы, то поперечное сечение утка приобретает форму, соответствующую створу. Эта форма существенно отличается от круга, эллипса или другой округлой формы, какой ее обычно принимают при описании взаимодействия основы и утка (на рисунке 1 геометрическая модель справа, вариант 2). В обоих случаях зубья берда вдавливают уточину в створ зева, перемещаясь на определенную величину вдоль оси и деформируя и уток, и основу.

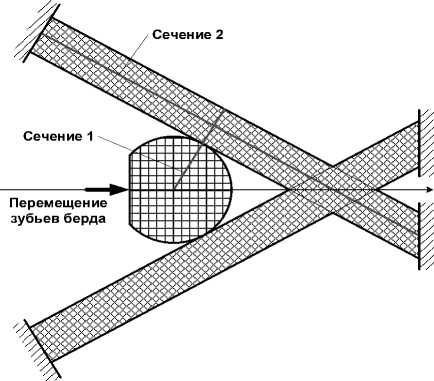
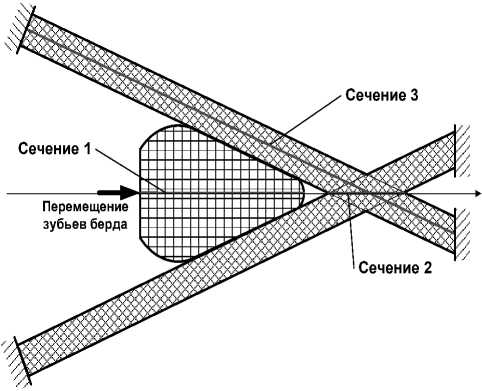
Рисунок 1 – Первый и второй варианты геометрической модели взаимодействия нити утка с системой основных нитей в процессе прибоя

МКЭ позволяет получить полную картину деформаций и напряжений в динамике их развития по всей площади системы, представленной моделями на рисунке 1. Для ее отображения и сравнения 2 вариантов взаимодействия системы «бердо – уток – основа» ограничимся распределениями интегрального показателя механического напряжения, известного как «напряжение по фон Мизесу» [8], вдоль линий 1 и 2 для варианта 1 и линий 1, 2 и 3 для варианта 2 в предельном правом положении берда. Эпюры этих распределений показаны на рисунке 2. Выбор сечений обусловлен результатами предварительного эксперимента по двумерным распределениям напряжения по фон Мизесу и компонентов тензоров напряжения и деформации и соответствует наиболее напряженным участкам сечений нитей. Распределение напряжений по фон Мизесу на сетке конечных элементов в состоянии максимальной деформации (максимального перемещения берда) показано на рисунке 3.

Моделирование проводилось в системе Comsol. В МКЭ использовались четырехугольные элементы сетки произвольной формы. Задача решалась как динамический процесс нарастающего перемещения поперечного сечения утка в створ нитей основы. По мере продвижения и уток, и нити основы деформировались. Уток подвергался сжатию и изменению формы сечения, а основные нити изгибались, вытягивались и утонялись, что следует из полученных эпюр для координатных компонентов тензоров напряжений, деформаций, их инвариантов и главных компонентов на протяжении всего времени прямого и возвратного перемещения берда. Материал нити утка – nylon 6.6, материал основных нитей – nylon 6 (Capron). Начальные модули упругости равны соответственно 1700 МПа, 1100 МПа.

Перемещение берда в направлении оси задавалось функцией A sin(π∙t / T), составляя половину периода синусоидальной функции и моделируя тем самым прямое и обратное движение берда при прибое относительно кромки полотна. В модельных переменных амплитуда A и время прибоя T были приняты равными единице, моменты отдельных этапов процесса отсчитывались и показаны на эпюрах рисунке 2 в долях от времени T.

Приведенные на рисунке 2 эпюры, как и распределения показателей деформации и механических напряжений по площади сечений рассматриваемой системы нитей, показали, что в случае жесткой уточной нити возникают локальные участки с весьма значительными напряжениями, во много раз превосходящими усредненные уровни напряжений, которые можно найти по известным конечномерным или одномерным моделям деформации. Эти участки сосредоточены в местах контакта нити утка с нитями основы. Большие напряжения могут провоцировать разрушение нитей основы, т. е. обрывы.

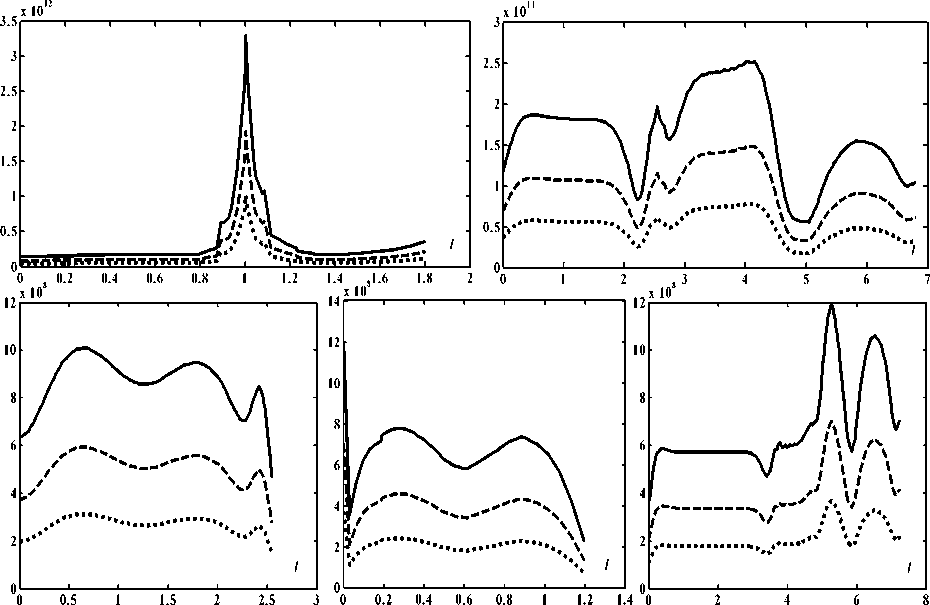
Рисунок 2 – Эпюры распределения механических напряжений по фон Мизесу вдоль сечений 1 и 2 модели 1 и вдоль сечений 1, 2 и 3 модели 2

Примечание: по оси абсцисс всех эпюр отложена линейная координата, отсчитанная вдоль сечений. Пунктирная, сплошная и штриховая линии эпюр построены для моментов времени, соответствующих 10 %, 50 % и 80 % от полного цикла перемещения берда от начала до конца прибоя.

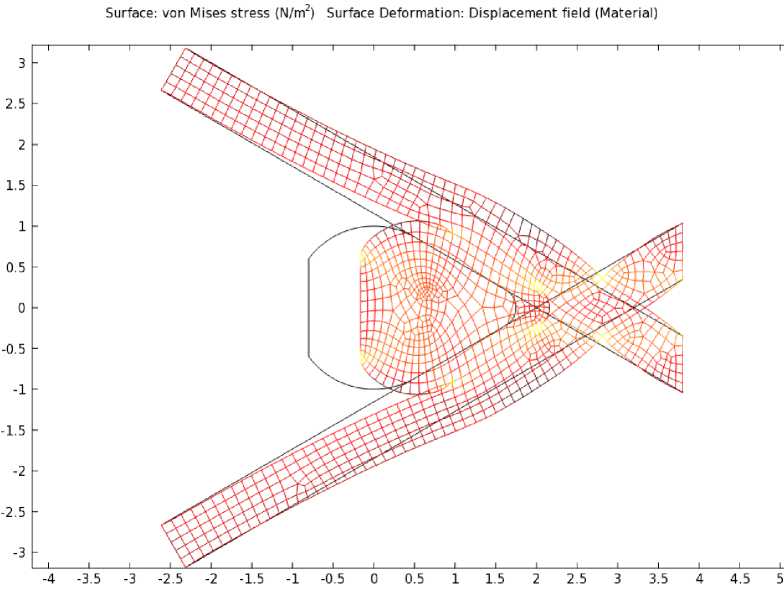
Рисунок 2 – Распределение механических напряжений в системе взаимодействующих уточной и основных нитей для 2-го варианта модели в момент наибольшего перемещения берда ( t = 50 % T )

Менее жесткие уточные нити принимают часть нагрузки на себя, изменяя свою форму. При этом давление со стороны утка на нити основы распределяется по большей площади. Это исключает возникновение участков с концентрацией больших механических напряжений и деформаций и приводит к практически равномерному распределению напряжений по площади сечений утка и нитей основы. Тем самым открывается возможность интенсифицировать процесс формирования ткани без опасности повышения обрывов нитей основы.

Отметим также характерную для обоих рассмотренных вариантов взаимодействия нитей утка и основы неравномерность распределения напряжений вдоль нитей основы в процессе прибоя. Вариации натяжения на соседних участках длины нитей варьируют в значительных пределах, создавая неодинаковые условия нагрузки. Учитывая, что нити основы имеют заметные вариации по прочности вдоль своей длины, а также силы трения основы о зубья берда, можно предположить, что неблагоприятное сочетание этих факторов также может явиться источником повышений обрывности основных нитей или нарушения структуры на локальных участках формируемого тканого полотна.