Компьютерная модель для расчёта спектральных характеристик светимости высокотемпературных потоков газа с частицами

Для решения разнообразных обратных задач мониторинга околоземной среды в инфракрасном (ИК) диапазоне, заключающихся в адекватной обработке и интерпретации измерений ИК датчиков с учётом влияния атмосферы, необходимо иметь, во-первых, адекватные специализированные модели наблюдаемых объектов и явлений и, во-вторых, детальную модель прохождения излучения в атмосфере от наблюдаемого объекта к измерителю. Такая потребность в согласованном расчёте спектров излучения объекта и пропускания атмосферы возникает при спектроскопическом исследовании факелов, образуемых высокотемпературными потоками смеси газа и частиц, в частности, выхлопными струями реактивных двигателей.

В данной работе рассмотрены методы расчёта эффектов переноса излучения в многокомпонентном газе с частицами и описана разработанная компьютерная модель, позволяющая проводить расчёт спектральных характеристик принимаемо- го датчиком ИК излучения факела с учётом геометрии наблюдения.

В модели учтены следующие явления.

• 1.    Cтруктура колебательно-вращательных полос поглощения–излучения газов, зависимость силы линий от температуры (вплоть до 3000 К).

• 2.    Излучение частиц, поглощение и рассеяние излучения частицами.

• 3.    Многократное рассеяние излучения на частицах.

• 4.    Излучение в состоянии неполного термодинамического равновесия, когда колебательная и поступательно-вращательная температура газов отличаются.

• 5.    Излучение в состоянии неполного термодинамического равновесия, когда температуры каждой фракции частиц различаются между собой и отличаются от температуры окружающего газа.

• 6.    Значительная вытянутость факела вдоль оси и сильное различие геометрических масштабов потока на разных участках.

• 7.    Сильная корреляция между структурами полос излучения факела и полос поглощения атмосферы.

Для учёта всех вышеперечисленных факторов использован метод, основанный на численном решении системы уравнений переноса излучения методом итераций. Для составления банка данных по линиям излучения использованы наиболее полная на сегодняшний день база данных колебательно-вращательных линий излучения атмосферных газов HITRAN и её высокотемпературная модификация HITEMP.

• II.    Система уравнений

и соотношений, описывающих перенос излучения в гетерогенной среде факела

Факел, образуемый высокотемпературным потоком смеси газа и частиц, является гетерогенной средой, в которой наряду с газовыми компонентами — продуктами выхлопа и составляющими спутного воздушного потока присутствуют дискретные частицы (например, частицы сажи, окиси алюминия) [1]. Для описания взаимодействия оптического излучения с гетерогенной поглощающей и рассеивающей средой используются уравнения переноса излучения [2, 3]:

l^Bv (Fj) = —av (F) Bv (F,F + Ev (F,F, (1)

Ev(F?) = 'yS [ Bv(F^)Xv(FS)d?+E?(r),

4 п

4 п где Bv (v,l)

(2)

спектральная плотность энергетической яркости излучения как функция координат F и направления l (частота v = 1 /А — параметр, А — длина волны), av(r) = ev(F) + 'v(F) — спектральный показатель ослабления (на единицу длины), Pv(F) — спектральный показатель поглощения, uv (F) — спектральный показатель рассеяния, Ev(F,l) — функция источника, состоящая из компонент, описывающих рассеяние (первое слагаемое) и истинное (тепловое) излучение Ev”(F), xv(г,1,1 ) — спектральная индикатриса рассеяния, нормированная так, что f 2v(тЦ*)dl' = 4п.

4 п

Спектральная плотность равновесного теплового излучения E ^” ( r ) определяется выражением

Ev” (F = в (r) EB (T (F)), где EBB (T (r)) — спектральная плотность излучения абсолютно чёрного тела (АЧТ) с температурой T:

E B^B ( T ( F)) =

2 hv3        1

c2 exp(hv/kT) — 1

(формула Планка).

Для заданного направления l наблюдения уравнение (1) можно представить в виде dBv (F(S) ,l) dS

—av (F( S)) Bv (F( S))+Ev (F( S)), (4)

где S — длина пути вдоль направления l

(dS > 0).

Решение уравнения (4) с начальным условием Bv(F(0),1) = Bvo(l), где Bvo(l) — спектральная плотность потока излучения внешнего источника, приводит к соотношению

Bv (F( S) ,l) = Bv o(l) e

S f av (r(S>'))dS'

s S

+ j e-P av №S')) dS Ev (F( p) ,0 dp,    (5)

o которое представляет собой запись уравнения переноса излучения в интегральной форме.

При наличии рассеяния для решения задачи переноса излучения можно использовать метод последовательных приближений. Для этого решение системы интегральных уравнений (5), (2) следует представить в виде

Bv (n)(F( S) ,l )= Bv o(l) e

S f av(r(S'))dS'

S

+

e

o

S f av (r(S'))dS'

p

Ev(n)(F,i) = 'BF j Bv(„-!)(F,r)Xv(F,l.t)d°+

4 п

+Ev” (F),                 (7)

n = 1, 2, ...

и использовать в качестве нулевого приближения:

Bv (0)(F( S) ,l ) = Bv o(l) e

S f av (r (-S'))d,S'

В силу линейности уравнений (6), (7) составляющие излучения, обусловленные тепловым излучением и внешней подсветкой, можно рассчитывать независимо.

Следует обратить внимание на то, что итерационная система интегральных соотношений (6), (7) записана для фиксированной частоты v . В реальных ИК датчиках спектры излучения измеряются с некоторым конечным спектральным разрешением A v . Следовательно, для получения практически значимых результатов необходимо получить решение уравнений переноса для некоторой достаточно мелкой сетки по v и провести интегрирование результатов в полосах шириной A v . Шаг мелкой сетки по v должен быть меньше характерной ширины спектральных линий поглощения газа. Такая процедура вычислений приводит к значительным вычислительным затратам, однако они неизбежны для обеспечения методической строгости и точности вычислений.

Выражение для показателя поглощения излучения в многокомпонентном газе в заданной точке ^r имеет вид

evg (r) = ^ k(г)eVk (т(r) P(r)),

P где Pk (г) — плотность к-й компоненты газа, eVk (T,P) — коэффициент поглощения k-й компоненты для излучения частоты ν , зависящий от давления P и температуры T.

Коэффициент поглощения e V_k ( T,P ) представляет собой суперпозицию вкладов отдельных спектральных линий:

eVk(T,P) = £ iFk(v - Vki,5ki), P где Ski — интенсивность i-й линии, Fk(v - Vki,^ki) — контур линий, Vki — несущая частота, ^γki — вектор параметров контура (главный параметр — полуширина контура).

Для лоренцевского контура спектральных линий [4–6], который справедлив для случая уширения за счёт столкновений между молекулами (низкие температуры и высокие давления):

^{1 Y k}i

Fk(v "ki,11**" n (v - mi)2 + ^ •

Для высоких температур и низких давлений доплеровское уширение линий становится более существенным, чем уширение за счёт столкновений [4]. Доплеровский контур линии выражается формулой

Fk (v-vki ,Yki) =

где α D

ν 0 c

V

1 ex [ / v - vik V1 Vnap         aD ,

2 kT ln2 m

— доплеровская по-

луширина линии, T — температура, m —

масса молекулы, c — скорость света, k —

постоянная Больцмана.

Согласно кинетической теории газов за-

висимости полуширины и интенсивности линий от температуры и давления определяются соотношениями [5, 6]:

Y ki ( p,t ) = ( T ) / ( ^ а^ P-p sk + Y^s_kf p k ) ,

S = S (To) Qr (To) Qv (To) Qr (T) Qv (T)    X

x exp

/1,439E'(T - T0)

TT 0

x 1 - exp(-1,439vik/Т)

1 - exp(-1,439vik/To)

X

(8)

где Y air , Y kef и S ( T 0 ) — полуширина и интенсивность линий при нормальных условиях ( P 0 = 1 атм., Т о = 273 К), Q _r ( Т ) и Q v ( Т ) — вращательная и колебательная частные суммы для газа, E' — энергия

нижнего уровня, p sk — парциальное давление k -й компоненты газа.

Процедура вычисления частных сумм подробно описана в [7]. Согласно [8] колебательная частная сумма вычисляется как произведение по всем степеням свободы i :

Q, (т ) = П(1

-

e

—

^ihc/kT } ^— di

i

где ω i — собственная частота колебаний, а d _i — вырожденность уровня.

Вращательные частные суммы вычисляются различными методами в зависимости от типа молекулы: линейного [9], сферического [10], симметричного [11] или асимметричного [12].

Банк данных по линиям поглощения газов сформирован на основе баз данных HITRAN [6] и HITEMP. База данных HITRAN предназначена в основном для

температур до 1000 К. Для более высоких температур необходимо использовать базу данных HITEMP. Она аналогична базе HITRAN, но содержит набор линий, существенных на температурах выше 1000 К (до 3000 К). В ней содержатся данные по трём основным продуктам сгорания: углекислому газу, воде и угарному газу.

Для расчётов поглощения и рассеяния излучения частицами с хорошим приближением можно предполагать, что частицы имеют сферическую форму. Показатель поглощения излучения сферическими частицами с дискретным распределением по размерам (фракциям) определяется соотношением [4]:

M

evp (f) = Пр (f) У^ npj (f) naj Ka (m,Pj), j=1

где n _pj (f ) — концентрация частиц j -й фракции [ 4 г], K a ( m,P j ) — фактор эффективности поглощения, m = n — i^ — комплексный показатель преломления материала частиц, a j — радиус частиц, P j = 2 nva j — волновой параметр. Точный расчёт функции K a ( т,р ) выполняется на основании теории Ми [13, 14]. Приближенно K a ( т,р ) можно рассчитать по формуле Ван-де-Хюльста [13]:

Ka = 2 Q (4 рр), где

Q (г) = 2 + г 1 < - + г-2( e-z — 1).

Расчёты по этой формуле хорошо соответствуют точным значениям.

В газодинамических факелах зачастую не достигается полного термодинамического равновесия [1]. Расчёт излучения факелов в таких условиях основан на использовании приближения частичного термодинамического равновесия, когда фракции частиц смеси имеют различные температуры, а газ имеет единую кинетическую температуру, единую вращательную температуру, равную кинетической температуре, и различные колебательные температуры для каждой молекулярной компоненты [15]. Заселенности колебательных уровней молекулярных компонент в этом приближении определяются распределением Больцмана.

В условиях интенсивной головной ударной волны распределение заселенности колебательных уровней может отличаться от больцмановского из-за того, что скорость колебательного возбуждения молекул в химических реакциях может быть сравнима с временем колебательной релаксации. Однако как показали расчёты для возможных параметров моделирования, головная ударная волна становится интенсивной в условиях спутного воздушного потока факела малой плотности, когда химические реакции практически не идут. Поэтому в данной модели влияние химических реакций на распределение заселенностей колебательных уровней молекул не учитывается.

В случае частичного термодинамического равновесия в формулы для ширины линии (как лоренцевской, так и доплеровской) необходимо подставлять кинетическую температуру, а формулы для излучения примут следующий вид:

формула (3) — рвв _ 2hv3

E.   — --:--:—т^—  :—“^— .

V       c 2 eh Д Ev/kT eh A Er /kTr   1 , формула (8) —

S =

S ( T 0 ) Q r ( T 0 ) Q v ( T 0 )

Q r ( T r ) Q v ( T v )

X

e - 1 , 439 Ev /Tv e - 1 , 439 ЕГ/Tr

X       e-1,439E' /Tо

1 _ _e - 1 , 439Д Ev/Tv e - 1 , 439Д Er/T

1 _ _e - 1 , 439 Vik/T о

где Tv и Tr — колебательные и вра- щательные температуры соответственно, E'v и E’r — энергии нижних колебательных и вращательных уровней энергии (E'v+ЕГ = E'), A Ev и A Er — разность верхней и нижней энергии колебательных и вращательных уровней (AEv + AEr = vik).

Учитывая, что вращательная энергия значительно ниже кинетической, формулы (9), (10) можно свести к виду (3) и (8), если заменить в последних равновесную температуру на колебательную.

• III.    Входные и выходные данные, основные блоки и банк данных модели

Входными данными модели являются:

• 1)    дата и время наблюдений (для учёта внешней подсветки);

• 2)    координаты датчика (высота, долгота, широта);

• 3)    координаты и положение факела в пространстве;

• 4)    высотные профили атмосферных параметров: давления, температуры, влажности — для заданных условий наблюдения;

• 5)    распределения параметров в поперечных сечениях факела: давления газа, парциальных плотностей компонент газа и фракций частиц, поступательной и колебательных температур газовых компонент, температур фракций частиц;

• 6)    параметры расчёта: пространственное разрешение, границы спектрального диапазона, спектральное разрешение.

Выходными данными модели являются:

• 1)    распределение спектральной плотности яркости факела B = f ( x,y ) (изображе-

• ние) в заданном спектральном диапазоне (x — продольная координата, y — поперечная);

• 2)    функция линейной (погонной) яркости в заданном спектральном диапазоне L = f (х) для заданного пространственного разрешения;

• 3)    спектральная плотность интенсивности излучения I = f ( А ) в заданном спектральном диапазоне с заданным спектральным разрешением.

Для численного решения задачи переноса лучистой энергии можно использовать метод Монте-Карло (см., например, [16, 17]) или метод последовательных приближений (в различных вариантах, см. [18, 19]). В данной модели использован метод последовательных приближений на основе соотношений (6), (7).

На рис. 1 представлена блок-схема алгоритма вычислений. Задачи, решаемые основными блоками модели, определены в табл. 1.

Таблица 1

№	Наименование блока	Решаемая задача
1	Инициализация	Инициализация памяти, запрос и проверка входных данных, выбор внутренних параметров моделирования
2	Расчёт переноса излучения в факеле	Определение пространственно-угловой функции спектральной плотности энергетической яркости внутри и на границе факела методом итераций
3	Расчёт спектральных характеристик излучения и поглощения для газовых компонент	Рассчитываются спектральные функции показателей поглощения газовых компонент с использованием банков данных HITEMP и HITRAN
4	Интерполяция данных на внутреннюю сетку	Интерполяция входных распределений параметров в поперечных сечениях факела на внутреннюю прямоугольную сетку
5	Расчёт спектральной плотности энергетической яркости внутри факела	Для заданной сетки угловых направлений и заданной длины волны интегрируется уравнение переноса
6	Расчёт составляющей излучения от внешней солнечной подсветки	Рассчитываются характеристики составляющей излучения от солнечной подсветки в узлах сетки
7	Расчёт рассеянной составляющей спектральной плотности яркости факела	Методом итераций рассчитывается составляющая спектральной плотности яркости факела, обусловленная внешней подсветкой
8	Расчёт спектральной функции пропускания атмосферы	Для заданной геометрии наблюдения и атмосферных профилей рассчитывается спектральная функция пропускания атмосферы с использованием банка данных HITRAN

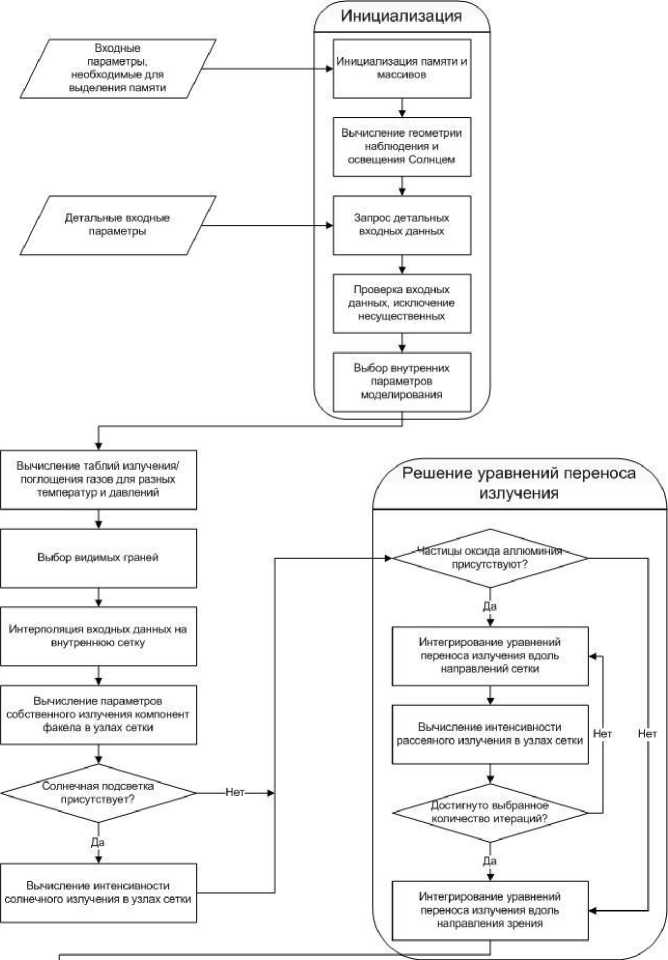
Рис. 1. Блок-схема вычислений спектральных характеристик излучения факела

Банк данных модели включает:

• —    банк данных HITEMP;

• —    банк данных HITRAN;

• —    банк данных по спектральным характеристикам поглощения и рассеяния частиц в зависимости от температуры.

• IV.    Некоторые результаты расчётов

Для проверки модели проведено сравнение с результатами аналогичных расчё- тов по другим моделям и с экспериментальными данными.

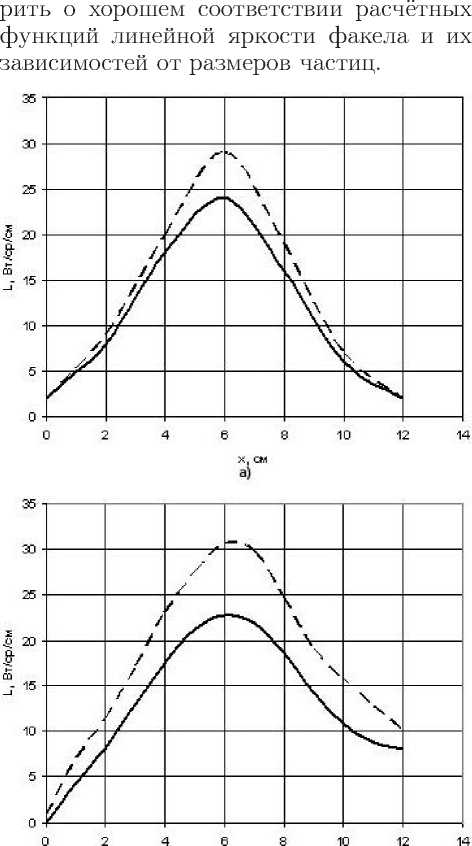
Для примера на рис. 2 представлены расчётные графики функций линейной яркости факела в зависимости от расстояния от среза сопла для двух размеров частиц: 1 мкм и 10 мкм. Графики, показанные на рис. 2а, взяты из [20]. Графики, показанные на рис. 2б, рассчитаны на описываемой здесь модели. Для расчётов использовались распределения параметров в поперечных сечениях факела, полученные на модели [21]. Для параметров потока на сре- зе сопла использовались значения, приведённые в [20]. Сравнение позволяет гово-

х6™

Рис. 2. Расчётные графики функций линейной яркости для двух размеров частиц. Размеры частиц: пунктир — 1 мкм, сплошные линии — 10 мкм

На рис. 3 представлены результаты лабораторных измерений в вакуумной камере функции линейной яркости факела (для параметров атмосферы на высоте 12 , 2 км) и соответствующие результаты расчёта на описываемой здесь модели. Экспериментальные данные и значения параметров потока на срезе сопла приведены в [22]. Из рисунка видно, что результаты моделирования неплохо соответствуют экспериментальным данным.

Для проверки функциональных возможностей разработанной модели были проведены расчёты спектральных характеристик светимости газодинамических фа- келов в различных условиях. Для расчётов распределений параметров в поперечных сечениях факела использовалась модель [21]. Для параметров потока на срезе сопла использовались значения, приведённые в [23]. Размер частиц полагался равным 1 мкм.

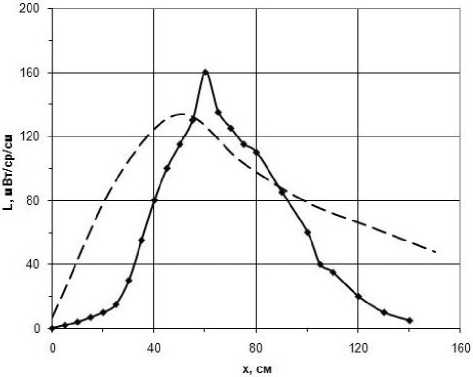
Рис. 3. Сопоставление результатов расчётов функции линейной яркости с экспериментальными данными. Сплошная линия — эксперимент, пунктир — расчёт

Рис. 4. Изображения факелов в полосе поглощения 2 , 7 мкм на высотах 5, 50, 120 км (сверху-вниз)

На рис. 4 представлены изображения факела (с повышенной контрастностью) в полосе поглощения углекислого газа и паров воды вблизи 2 , 7 мкм на высотах 5, 50, 120 км. Поглощение излучения в атмосфере не учитывалось. Направление зрения перпендикулярно оси факела. Изме-

ТРУДЫ МФТИ. — 2009. — Том 1, № 3 нение структуры ИК изображений факела с увеличением высоты соответствует характерным изменениям пространственных распределений основных параметров факела в зависимости от высоты, в частности, температуры газа и частиц. Линейные размеры указаны в относительных единицах.

На рис. 5 представлены графики спектральной плотности излучения факела в целом с высоким разрешением по волновому числу v (0,01 см~ 1) для высот 5 и 50 км (поглощение излучения в атмосфере не учитывалось). Спектр излучения меняется существенно, что обусловлено значительным изменением пространственных распределений температуры, давления и концентраций компонент в факеле. На графике спектральной плотности для высоты 50 км нижний уровень излучения («пьеде- стал») обусловлен сплошным спектром излучения частиц.

На рис. 6 продемонстрировано влияние поглощения излучения в атмосфере на трассе наблюдения на спектр излучения факела на высоте 15 км, принимаемого космическим датчиком в полосе 2–3 мкм. На рис. 6а показана спектральная зависимость коэффициента пропускания атмосферы в зависимости от длины волны (в мкм) вдоль луча с перигеем 15 км (горизонтальная трасса). На рис. 6б представлены спектры излучения факела, рассчитанные без учёта поглощения в атмосфере и с учётом поглощения на трассе. Видно, что полосы максимума поглощения в атмосфере соответствуют максимуму излучения факела без учёта поглощения в атмосфере и минимуму принимаемого излучения при учете поглощения.

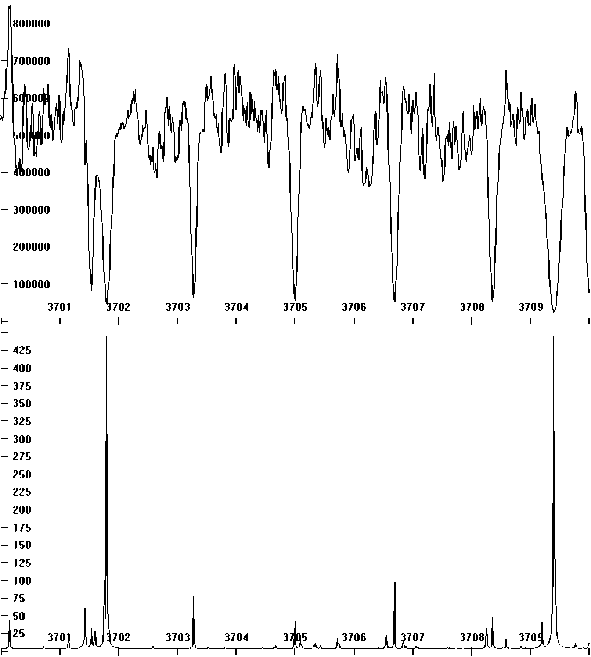
Рис. 5. Тонкая структура спектральной плотности излучения (Вт / см ^{- 1} / стер) факела в зависимости от волнового числа v (см ^{- 1} ) для высоты 5 км (вверху) и 50 км (внизу)

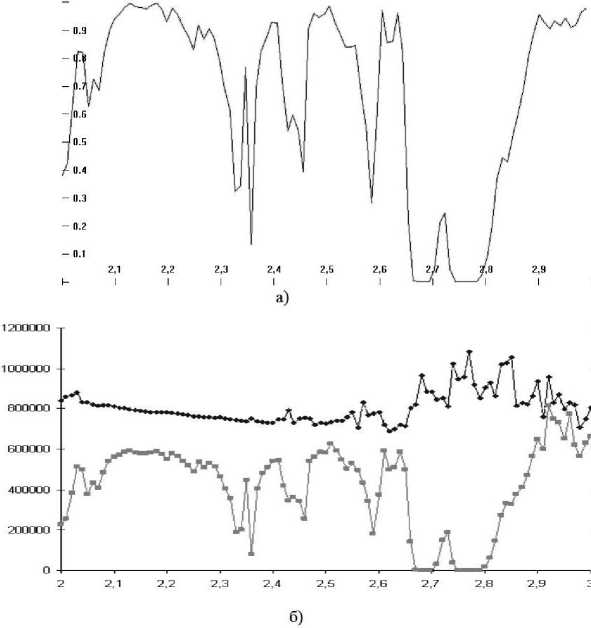
Рис. 6. а) — спектральная зависимость коэффициента пропускания атмосферы в зависимости от длины волны вдоль луча с перигеем 15 км; б) сравнение спектра излучения факела (Вт / мкм / с тер) без учёта атмосферного поглощения (верхний график) и с учётом поглощения на трассе (нижний график)

• V.    Заключение

• 1.    Разработана компьютерная модель для расчёта спектральных характеристик светимости высокотемпературных потоков газа с частицами. Модель основана на численном решении методом последовательных приближений системы уравнений переноса излучения в многокомпонентном газе с частицами. В модели учтены все основные явления, влияющие на спектральные характеристики светимости высокотемпературных неравновесных потоков смеси газа и частиц в различных условиях.

• 2.    Сравнение результатов расчётов на разработанной компьютерной модели с аналогичными расчётами по другим моделям и с экспериментальными данными показывает их хорошее согласие.

• 3.    Для проверки функциональных возможностей разработанной модели проведены расчёты спектральных характеристик светимости газодинамических факелов в различных условиях. Полученные результаты расчётов соответствуют закономер-

• ностям изменения спектральных характеристик светимости факелов при изменении пространственных распределений параметров факела в зависимости от условий расчётов.