Компьютерная модель теплообмена в установке непрерывного литья и прессования цветных металлов
Автор: Скуратов А.П., Потапенко А.С.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Рубрика: Журнал СФУ. Техника и технологии: 2017 год (том 10, номер 8)
Статья в выпуске: 8 т.10, 2017 года.
Бесплатный доступ
На основе программного комплекса Ansys CFX разработана трехмерная компьютерная модель сложного теплообмена в установке непрерывного литья и прессования цветных металлов. Рассмотрены особенности построения расчетной сетки и решения системы дифференциальных уравнений энергии для обрабатываемого металла и элементов установки. Изучена динамика процесса литья и прессования алюминиевого сплава на опытной лабораторной установке. Определены расчетные температуры металла и элементов опытного образца установки. Проведена экспериментальная оценка достоверности результатов моделирования и показана адекватность разработанной компьютерной модели.
Установка, непрерывное литье и прессование, компьютерная модель, программный комплекс ansys, теплообмен, эксперимент, алюминиевый сплав
Короткий адрес: https://sciup.org/146115266
IDR: 146115266 | УДК: 66.971 | DOI: 10.17516/1999-494X-2017-10-8-1019-1030
Текст научной статьи Компьютерная модель теплообмена в установке непрерывного литья и прессования цветных металлов
Процессы обработки цветных металлов и сплавов включают в себя такие основные металлургические переделы, как литье заготовки, пластическую деформацию и термообработку. Тенденцией развития металлургической отрасли является совмещение этих переделов в одну непрерывную технологическую линию. Разнообразные модификации установок непрерывного литья и прессования цветных металлов получили широкое применение в металлообрабатывающей отрасли промышленности. Протекающие в данных установках термомеханические процессы имеют сложный характер, зависящий от выбранной технологии и особенностей их конструкции [1-3].
Основным технологическим параметром совмещенного процесса непрерывного литья и прессования (НЛиП) является промежуток времени между заливкой в инструмент расплава и входом закристаллизовавшегося металла под дугообразный сегмент с матрицей. Правильный выбор режима затвердевания слитка существенно влияет на формирование его структуры и свойств [4]. Величина указанного промежутка времени зависит от таких факторов, как начальная температура расплава, удаленность матрицы от места заливки, скорость движения канавки с металлом, интенсивность его охлаждения, размеры поперечного сечения и ряд др. [5]. Сложный характер влияния и взаимодействия этих факторов изучен недостаточно, что затрудняет решение задачи по повышению эксплуатационной надежности действующих и проектирование новых установок. Поэтому актуальна задача проведения на базе современных математических моделей сложного теплообмена теоретических исследований, направленных на изучение температурно-временных зависимостей процесса литья-прессования цветных металлов.
При решении задачи многофакторного исследования нового технического объекта требуется использование различных приближений и численных методов, позволяющих предсказать его поведение без проведения, как правило, дорогого и затруднительного эксперимента. В настоящее время в связи с развитием вычислительной техники и созданием современных программных продуктов стало возможным широкое применение такого вида теоретического исследования, как компьютерное моделирование [6-8].
Целью работы является разработка на базе программного комплекса ANSYS CFX компьютерной модели сложного теплообмена в установке НЛиП цветных металлов и сплавов с горизонтальным карусельным кристаллизатором.
Компьютерная модель экспериментальной установки
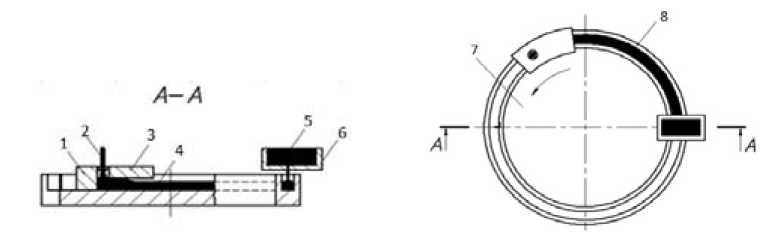
Экспериментальная установка НЛиП проста в конструктивном исполнении элементов, которые работают в условиях высоких тепловых нагрузок (рис. 1).
a
b
Рис. 1. Схема установки непрерывного литья и прессования с горизонтальным карусельным кристаллизатором: a – вид сбоку: 1 – упор матрицы; 2 – пресс-изделие; 3 – неподвижный дугообразный сегмент; 4 – затвердевший слиток; 5 – расплав металла; 6 – дозатор; b – вид сверху: 7 – колесо-кристаллизатор; 8 – кольцевая канавка
Fig. 1. Installation diagram of CCME with a horizontal carousel crystallizer pan: a – side view: 1 – matrix support; 2 – molding; 3 – stationary arc-shaped segment; 4 – hardened ingot; 5 – molten metal; 6 – batcher. b – top view; 7 – crystallizing wheel; 8 – annular groove
В рассматриваемой установке НЛиП жидкий металл 5 заливается через дозатор 6 в ручей 8 вращающегося рабочего колеса 7 и кристаллизуется до входа в камеру прессования, образованную на участке сопряжения ручья с матрицедержателем 3 . Слиток 4 , поступая в камеру прессования, выдавливается в отверстие матрицы 1 в виде пресс-изделия 2 . Процессы заливки жидкого металла в канавку, его кристаллизация и прессование протекают непрерывно [9].
Для изучения тепловой работы установки разработана ее трехмерная компьютерная модель с использованием программного продукта Solid Works. Полученная геометрия импортирована в расчётный модуль Ansys CFX, где производится дальнейшая подготовка модели, для исследования тепловой работы установки (рис. 2).
Модель установки НЛиП построена на основе решения сопряженной задачи радиационноконвективного теплообмена нескольких систем: «обрабатываемый металл – кристаллизатор»; «обрабатываемый металл – дугообразный сегмент»; «кристаллизатор – изоляционный слой – подшипники»; «кристаллизатор – воздушная прослойка – корпус»; «поверхность элемента установки – окружающая среда» [10].
Для создания расчётной сетки установка разбивается на 8 доменов. Домен корпус (CORPUS), состоящий из 181088 элементов. Домен кристаллизатор (CRISTALLYZER), состоящий из 1899260 элементов. Домен изоляционный слой (INSULATOR), состоящий из 38217 элементов. Домен дугообразный сегмент с матрицей (MATRIX), состоящей из 46705 элементов. Домен подставки дозатора (PODSTAVKA), состоящей из 251196 элементов. Домен воздушной прослойки между кристаллизатором и корпусом (SOLIDAIR). Домен обрабатываемого расплава разделён на два: (GROOVE) – участок от места заливки до дугообразного сегмента с матрицей (зона кристаллизации), состоящий из 1074651 элемента, и (GROOVE 2) – участок обрабатываемого металла, находящегося под дугообразным сегментом (зона прессования) и состоящий из 185461 элемента. Размер сетки в итоговом расчете всей модели составил 3.7 млн ячеек. Сетка – 1021 –

a b
Рис. 2. Трёхмерная компьютерная модель установки НЛиП: а – геометрия установки; b – расчётная сетка контрольных объёмов
Fig. 2. Three-dimensional computer model of the CC&P installation: a – the geometry of the installation; b – calculated grid of reference volumes строится в автоматическом режиме по следующим правилам: между доменами внутри расчетной области узлы стыкуются по правилу «узел-в-узел».
Размер ячейки внутри доменов «GROOVE» и «GROOVE 2», содержащих жидкую фазу, составляет 0,8 мм. Пристеночный слой размещается при помощи 10 ячеек на расстоянии 2 мм от стенки с коэффициентом роста 1,2. Конфигурация сетки внутри домена с жидкой фазой подбиралась минимальной.
В остальных областях размер ячейки не фиксируется. На всех поверхностях задается пограничный слой из трех ячеек на расстоянии 1 мм от стенки. В домене кристаллизатора задаётся сгущение сетки в месте контакта с обрабатываемым металлом. На основе полученной сеточной модели создаётся расчётная модель путём наложения граничных и начальных условий, параметров моделируемых процессов и задания настроек решателя.
При определении параметров надёжной работы установки НЛиП с водяной системой охлаждения был добавлен домен «WATER 1», соответствующий змеевику, расположенному на дугообразном сегменте, и содержащий 382000 элементов. Домены «WATER 2» и «WATER 3» соответствуют кольцевым профилированным каналам, расположенным в корпусе на внутренней и внешней стороне относительно подшипников, и состоят из 135000 и 102000 элементов соответственно.
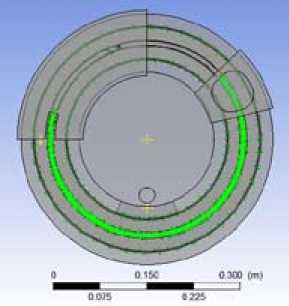
Домен «GROOVE» и «GROOVE 2» (рис. 3) описывается при помощи модели несжимаемой жидкости, решается система уравнений Навье-Стокса для ламинарного течения жидкости и уравнение теплопроводности. Причём в объёме домена «GROOVE 2» задаётся выделение объёмного источника теплоты в зависимости от температуры обрабатываемого сплава (теплота, выделяемая от пластической деформации). На поверхности домена «GROOVE 2» задаётся поверхностный источник теплоты (теплота, выделяемая от трения о стенки кристаллизатора и дугообразный сегмент).
В модели дополнительно задаются функции, определяющие теплофизические характеристики обрабатываемого расплава в зависимости от его текущей температуры: теплопрово-
а
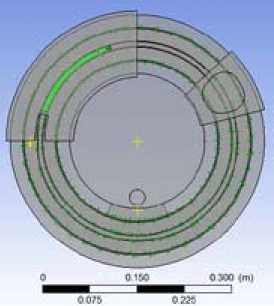
Рис. 3. Домены компьютерной модели: а – «GROOVE»; b – «GROOVE 2»
Fig. 3. Computer model domains: а – «GROOVE»; b – «GROOVE 2»
b
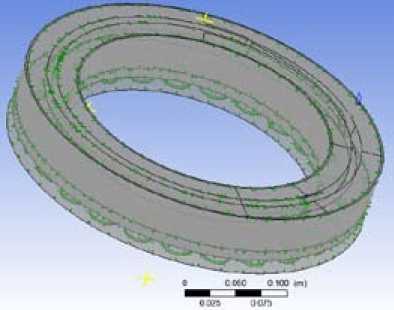
Рис. 4. Результат наложения граничных условий в компьютерной модели
Fig.4. The result of imposing the boundary conditions in the computer model
дность, теплоемкость, плотность, коэффициент поверхностного натяжения. При этом функциональная зависимость учитывает изменение теплоемкости и теплопроводности расплава при выделении скрытой теплоты его фазового превращения.
В результате наложения на расчётную модель граничных и начальных условий, она приобретает вид, представленный на рис. 4 (здесь отсутствует корпус, подставка и дугообразный сегмент).
Математическая модель теплообмена представляет собой систему дифференциальных уравнений сохранения энергии. Уравнение энергии включает члены, отвечающие за внутреннее тепловыделение при обработке сплава в процессе кристаллизации и прессования. Для моделирования переноса хладагента решаются уравнения Навье-Стокса, сохранения массы и импульса.
Нелинейное трехмерное уравнение сохранения энергии для обрабатываемого металла и элементов установки записывалось в виде субстанциональной производной:
ρ iсi ( T ) i =ρ iсi ( T ) i +ρ iсi ( T ) wi i =∇ ( λ i ( T ) ∇ Τ i ) + q вн i , (1)
где Т \ = Т\(х,у, z, т) - поле температур в i -м элементе; p i , c i и X i - плотность, объёмная теплоёмкость и теплопроводность i -го элемента; w i – скорость движения i -го элемента вдоль оси Z ; q вн i ( x,y,z, τ) – внутреннее тепловыделение при фазовом переходе в i -м элементе.
Уравнение (1) дополняется краевыми условиями:
– начальными условиями, определяющими начальное распределение температуры элементов установки Т i :
T i = T ( x , y , z , τ = 0) = T 0 i ( x , y , z );
– граничными условиями, формируемыми для различных граничных поверхностей Г i :
∂ T λ
∂ n
= ± qi , Г i
где qi – условия радиационно-конвективного теплообмена на границе поверхности i -го элемента установки Г i ; q i > 0 – поток направлен внутрь элемента i .
В модели, согласно рекомендациям [11, 12], граничные условия третьего рода (3) записывались в следующем общем виде:
q i = α i ( T Гi - T Гi + 1(0) ), (4)
где α i – соответствующей данной поверхности Гi коэффициент теплоотдачи, Вт/(м2·К); TГi и T Гi+1 (0) – температуры i -той поверхности ( Г i ) или окружающей среды ( Г 0 ), К.
Внутренние тепловыделения при фазовом переходе характерны для домена с металлом «GROOVE» и «GROOVE 2», для остальных элементов q вн i = 0. Скорость движения w i относительно оси Z присуща вращающимся элементам изучаемой системы: кристаллизатора «CRISTALLYZER» и металла «GROOVE». Для остальных элементов w = 0. i
Так как расплав обрабатываемого металла проходит две теплотехнические зоны (зоны кристаллизации расплава и прессования) [13], то величина qвнi в уравнении (1) принимает вид qBHt = ^h+ S'h, (5)
где S ^ - внутреннее тепловыделение при фазовом переходе (учитывается при решении уравнения теплопроводности в домене «GROOVE» и «GROOVE 2»); Sh - тепловыделение от сил контактного трения и сил деформации обрабатываемого металла (учитывается при решении уравнения теплопроводности в домене «GROOVE 2»).
В общем виде значение 5 ^ определяется выражением
S - 1 гишТ-у (6)
Hq
В модели теплота затвердевания L отдельно не учитывалась, а включалась в величину эффективной теплоёмкости сэ ф . Эта величина является разрывной энергетической характеристикой тепловых процессов с фазовыми переходами, зависящей в кристаллизующейся зоне от доли твёрдой фазы ψ. Принимая, что ψ зависит от локальной температуры T в условиях квазиравновесия, когда 5 ^ выделяется внутри интервала кристаллизации, можно записать [11, 12]
Сэф(Т)
Сж при Т > Тцч;Сж(1 -т^ + СтФ + Ь^ при Tsol <Т< Т^ ;
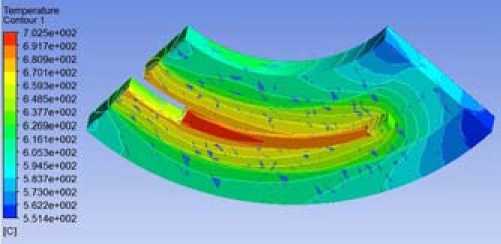
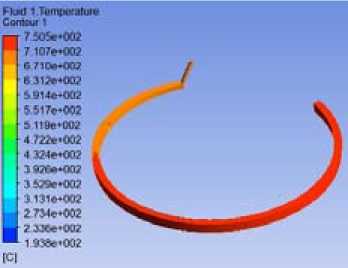
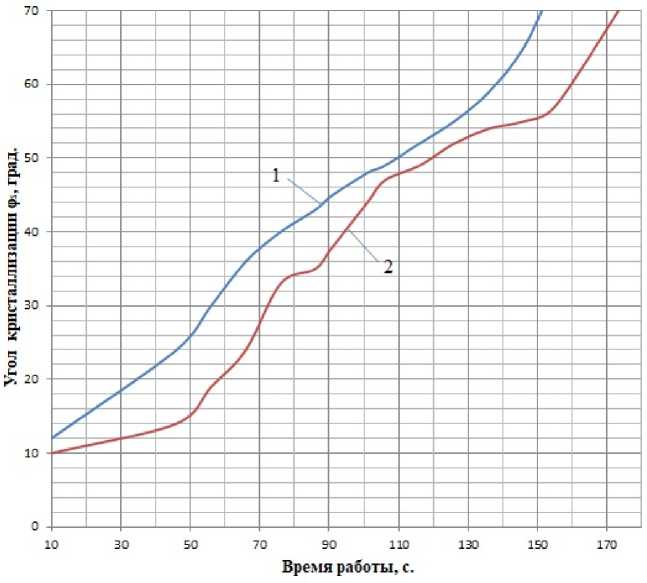
Ст при T Отметим, что для уточнения решаемой задачи в уравнение (1) вводится величина эффек- тивного коэффициента теплопроводности λэф, который также считается функцией доли твердой фазы ψ: Лэф(П = I Лж при т > Tliq; Лж(1-^)+Лт^ при T Учёт тепловыделения от сил контактного трения и сил деформации обрабатываемого металла учитывался в модели за счёт добавления объёмного источника теплоты [6]: " D^ QTp + Qg . Здесь qтр – тепловыделение от преодоления сил контактного трения с неподвижным инструментом и стенками кристаллизатора (поверхностный источник тепловыделений); qд – тепловыделение от работы пластической деформации (объёмный источник тепловыделения для прессования с боковым истечением деформируемого металла): Чд = CTS(T, e, f)(1,45A + 0,8)62Av0, где λ – коэффициент вытяжки; b – ширина канавки колеса; v0 – скорость подачи заготовки в контейнер; σS(T, ε, ξ) – сопротивление деформации материала заготовки. Теплота от преодоления сил трения определяется выражением [6] qTp = 4bas(T,e,^')4RVvo где R – средний радиус по ширине канавки колеса кристаллизатора; µ – коэффициент трения. При моделировании теплообмена между корпусом и кристаллизатором (домен «SOLIDAIR») тепловой поток q , передаваемый через цилиндрический воздушный зазор от i, внешней поверхности кристаллизатора к внутренней поверхности корпуса, определяется по уравнению (4), где величина αi имеет вид а=Хв / 5з +8пр Со [(ТГ 1 /100)4- (ТГ2/100)4] ( ТГ1 - ТГ 2) Здесь λв – теплопроводность воздуха; εпр – приведенная степень черноты системы из двух поверхностей (корпуса и кристаллизатора); С0 – коэффициент излучения абсолютно черного тела; δз – ширина воздушного зазора; ТГ1 и ТГ2 – температуры кристаллизатора и корпуса. При оснащении установки водяной системой охлаждения дугообразного сегмента (Домены «WATER 1», «WATER 2» и «WATER 3») величина αi представляет собой коэффициент теплопередачи Кохл, определяемый по соотношению а,- - Кохл 1, 1/адс +5дс / Хдс+1/ авод где δдс и λдс – толщина и коэффициент теплопроводности материала дугообразного сегмента; αдс и αвод – соответственно коэффициент теплоотдачи от затвердевшего металла к поверхности дугообразного сегмента и от внутренней поверхности змеевиков к воде. Отметим, чтопереностеплотывнутритвердыхтел (Домены «CORPUS», «CRISTALLYZER», «MATRIX», «PODSTAVKA» и «INSULATOR») описывается в модели уравнением теплопроводности. Результаты моделирования Оценка адекватности модели проведена путем сравнения результатов моделирования с экспериментальными данными, полученными на установке с горизонтальным кристаллизатором без принудительного охлаждения ее элементов. Исследовался процесс НЛиП сплава алюминия АК-12. В расчетах расплав с массовым расходом 9 г/с заливается в кристаллизатор при температуре 750 °C (граничное условие Inlet) через дозатор с диаметром выходного сечения 1,8 мм (в данной модели не рассматривается), установленный на зафиксированной относительно корпуса подставке. В граничных условиях Outlet задается выход затвердевшего алюминия из модели с соответствующим расходом. Направление вращения кристаллизатора по часовой стрелке. Температура окружающей среды составляет 20 °С. Расчетный коэффициент теплоотдачи конвекцией от внешних поверхностей в окружающую среду, за исключением зеркала расплава, составляет 10 Вт/(м2·К). Вращающийся кристаллизатор переносит затвердевающий расплав до дугообразного сегмента с матрицей. Для моделирования этого процесса в компьютерной модели задается вращение обрабатываемого металла. При этом используется модель подвижной стенки путем учета в каждой пристеночной ячейке вектора скорости, соответствующего темпу вращения 2 об/мин. Для кристаллизатора и изоляционного слоя задавался аналогичный по величине и направлению вектор скорости, моделируя, таким образом, их вращение. Для исследуемого теплового процесса граничные условия третьего рода (3) формируются в соответствии со схемой, представленной на рис. 5, для поверхностных границ Гi в осевых направлениях Z и X поперечного сечения установки. На схеме индексы i в координатах Zi и Xi указывают на соответствующую поверхность Гi и условия ее теплообмена в установке: – 0, 1, 2, 3 и 4 в направлении Z представляет теплообмен между соответственно корпусом и окружающей средой (Z0), корпусом и подшипником (Z1), подшипником и кристаллизатором (Z2), канавкой кристаллизатора и расплавом (Z3), кристаллизатора с расплавом и окружающей средой (Z4); – 1, 2, 3 и 4 в направлении X представляет теплообмен между соответственно канавкой кристаллизатора и расплавом (X1), кристаллизатором и корпусом через воздушную прослойку (X2, X3), корпусом и окружающей средой (X4). Таким образом, для приведенных выше граничных поверхностей Гi значение αi в уравнении (4) определялось или как линейное, учитывающее только конвективную составляющую теплообмена (поверхности Z1, Z2, Z3, X1, X3), или как нелинейное, учитывающее конвективную и лучистую составляющие теплообмена (поверхности Z0, Z4, X2, X4). В по-– 1026 – Рис. 5. Схема к определению в модели граничных условий: 1 – корпус; 2 – воздушный зазор между корпусом и кристаллизатором; 3 – кристаллизатор; 4 – канавка кристаллизатора с расплавом; 5 – подшипник Fig. 5. Scheme to determine the boundary conditions in the model: 1 – housing; 2 – air gap between the body and the crystallizer; 3 – crystallizer; 4 – the groove of the crystallizer with the melt; 5 – bearing следнем случае αi представляет собой сумму коэффициентов теплоотдачи конвекцией αi,k и излучением αi,л: а,- = а,-,к + а,-,л = а к ,к + £пр С0 [(ТГ 1 /100)4 - (ТГ2/100)4] (ТГ1 — ТГ 2) В результате моделирования определено изменение температуры каждого из элементов установки в процессе её работы. На рис. 6 изображено распределение расчетной температуры элементов установки при достижении стационарного теплового режима. Видно, что наибольший прогрев корпуса происходит в месте контакта с дугообразным сегментом (рис. 6c). Связано это со значительным тепловыделением в этом элементе установки за счет пластической деформации металла и сил контактного трения. При этом определено, что в процессе работы проектной конструкции установки без принудительного охлаждения ее элементов температуры дугообразного сегмента и обрабатываемого металла превышают точку солидуса для сплава АК-12. В результате металл непосредственно перед прессованием под дугообразным сегментом находится еще в жидкой фазе, что нарушает технологический процесс. Полученные при численном исследовании сложного теплообмена в установке НЛиП результаты хорошо согласуются с экспериментальными данными [13], подтверждают адекватность компьютерной модели и возможность отработки на ней инженерных решений. Так, например, при моделировании литья-прессования сплава АК-12 угол затвердевания расплава φs спустя 75, 155 и 218 с от начала работы установки составил соответственно 40, 74 и 116°. При проведении эксперимента в том же временном интервале этот угол равнялся соответственно 33, 57 и 97° (рис. 7). Расхождения в изменении угла затвердевания φs между экспериментом и расчётом главным образом связаны с тем, что при моделировании точка солидуса определялась во – 1027 – а b c d Рис. 6. Распределение температуры в элементах установки после ее выхода на стационарный тепловой режим: а – корпус; b – кристаллизатор; c – дугообразный сегмент; d – обрабатываемый сплав Fig. 6. Distribution of temperature in the elements of the plant after its release on stationary thermal conditions: a – housing; b – crystallizer; c – arcuate segment; d – processed alloy всем сечении кристаллизующегося металла, а не локально при измерении температуры термопарой в ходе эксперимента. Кроме того, следует учитывать погрешность термометра с аналоговым выходом (±1,5 %) и определённую тепловую инерционность хромель-алюмелевой термопары. Заключение Разработана динамическая компьютерная трехмерная модель установки НЛиП, учитывающая условия сложного теплообмена между её элементами и наличие хладагента для отбора от них избытка теплоты, движение горизонтального кристаллизатора и поступающего расплава, зависимость его теплофизических характеристик от температуры, а также образование теплоты при фазовом переходе от преодоления сил контактного трения и деформации металла. Определены температуры элементов установки после выхода ее на стационарный тепловой режим. Показано, что эксплуатация конструкции экспериментальной установки без принудительного охлаждения сопровождается значительным перегревом ее элементов при выходе на стационарный тепловой режим. В результате нарушается технологический процесс НЛиП, что требует разработки эффективной системы охлаждения наиболее теплонапряженных участков установки. Рис. 7. Динамика изменения угла затвердевания φs расплава АК-12: 1 – расчет; 2 – эксперимент Fig. 7. Dynamics of the solidification angle φs of the melt of AK-12: 1 – calculation; 2 – experiment Сравнение результатов моделирования и экспериментальных данных показали адекватность разработанной компьютерной модели и возможность отработки на ней инженерных решений.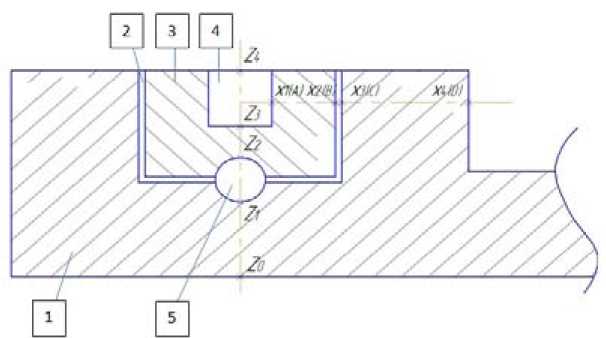

Список литературы Компьютерная модель теплообмена в установке непрерывного литья и прессования цветных металлов
- Баузер М., Зауер М., Зигерт К.М. Технология прессования металлов, пер. с немецкого. М., АЛЮСИЛ МВ и Т, 2009. 918 с
- Бережной В.Л. Базовые технологии и оборудование будущего в производстве пресс-изделий, Технология легких сплавов. 2006, 1-2. С. 52-60
- Duncas H.F. Continuous copper casting and rolling. Metals and Materials. 1972. v. 6. 2. Р. 102
- Grzyb R., Misiolek Z. The experimental investigations on the Force Parameters and metal flow in the combined process of Rolling and Extrusion. Archiwum Hutnitwa. 1983. 3. Vol. 28. P. 321-340
- Бережной В.Л. Щерба В.Н., Батурин А.И. Прессование с активным действием сил трения. М., Металлургия, 1988. 296 с
- Довженко Н.Н., Беляев С.В., Сидельников С.Б., . Прессование алюминиевых сплавов: моделирование и управление тепловыми условиями: монография. Красноярск: Сиб. федер.ун-т, 2009. 256 с
- Stebunov S., etc. Development and industrial verification of Q-Form-Extrusion program for simulation profile extrusion. Proceeding of International Conference of Extrusion and Benchmark, Dortmund, Germany. 2009. P. 41-42
- Скуратов А.П., Махов Д.И., Павлов Е.А. Компьютерное моделирование и оптимизация процесса литья слитков платины. Журнал Сиб. федер. ун-та. Серия Техника и технологии, 2014. 7(1). С. 96-102
- Горохов Ю.В., Солопко И.В., Константинов И.Л. Основы проектирования конструктивных параметров установки непрерывного литья-прессования метало. Вестник МГТУ им. Г.И. Носова. 2009. 3. С. 20-23
- Скуратов А.П., Потапенко А.С., Горохов, Ю.В. Исследование тепловой работы установки непрерывного литья и прессования алюминия в переходном режиме. Журнал Сиб. федер. ун-та. Техника и технологии, 2017. 10 (3). С. 337-345
- Самойлович Ю.А., Тимошпольский В.И., Трусова И.А. . Стальной слиток, В 3 т. Т. 1. Управление кристаллической структурой. Мн., Беларуская навука, 2000. 583 с
- Лисиенко В.Г., Лобанов В.И., Китаев Б.И. Теплофизика металлургических процессов. М., Металлургия, 1982. 240 с
- Потапенко А.С., Скуратов А.П., Горохов Ю.В. Динамика затвердевания алюминиевого сплава при нестационарном тепловом режиме установки непрерывного литья и прессования. Вестник Иркутского гос. техн. ун-та, 2017. 21 (7). С. 109-118. [


