Компьютерная реализация поиска в глубину

Актуальность исследования объясняется тем, что в настоящее время, существует множество разработанных алгоритмов для решения различных задач из самых разных областей человеческой деятельности.

Очевидно, что наиболее понятный и полезный для человека способ представления графа — изображение графа на плоскости в виде точек и соединяющих их линий — будет совершенно бесполезным, если мы захотим решать с помощью ЭВМ задачи, связанные с графами. Алгоритм поиска (или обхода) в глубину позволяет построить обход ориентированного или неориентированного графа, при котором посещаются все вершины, доступные из начальной вершины.

Отличие поиска в глубину от поиска в ширину заключается в том, что результатом алгоритма поиска в глубину является некоторый маршрут, следуя которому можно обойти последовательно все вершины графа, доступные из начальной вершины. Этим он принципиально отличается от поиска в ширину, где одновременно обрабатывается множество вершин, в поиске в глубину в каждый момент исполнения алгоритма обрабатывается только одна вершина. С другой стороны, поиск в глубину не находит кратчайших путей, зато он применим в ситуациях, когда граф неизвестен целиком, а исследуется каким-то автоматизированным устройством.

Обход в глубину можно представить себе следующим образом. Пусть исследователь находится в некотором лабиринте (графе) и он хочет обойти весь лабиринт (посетить все доступные вершины в графе). Исследователь находится в некоторой вершине и видит ребра, исходящие из этой вершины.

Видим, что алгоритм является рекурсивным — для обхода всего графа нужно переместиться в соседнюю вершину, после чего повторить для этой вершины алгоритм обхода. Но возникает проблема зацикливания — если из вершины A можно перейти в вершину B, то из вершины B можно перейти в вершину A и рекурсия будет бесконечной. Для борьбы с рекурсией нужно применить очень простую идею — исследователь не должен идти в ту вершину, в которой он уже был раньше, то есть которая не представляет для него интерес (считаем, что интерес для исследователя представляют только вершины, в которых он не был ранее).

Поскольку целью обхода в глубину зачастую является построение дерева обхода в глубину, то сразу же будем хранить предшественника для каждой вершины.

Алгоритм обхода в глубину позволяет решать множество различных задач. Например, реализуем при помощи алгоритма обхода в глубину подсчет числа компонент связности в неориентированном графе.

Для этого будем обходить все вершины графа и проверять, была ли очередная вершина посещена ранее. Если не была – то это означает, что найдена новая компонента связности, для выделения всей компоненты связности необходимо запустить DFS от этой вершины.

Так же можно проверить граф на двудольность. Граф называется двудольным, если его вершины можно разбить на два множества так, что концы каждого ребра принадлежат разным множествам. Иными словами, можно покрасить вершины графа в два цвета так, что концы каждого ребра покрашены в разный цвет.

Алгоритм DFS для каждого ребра будет проверять цвет конечной вершины этого ребра. Если вершина не была посещена, то она красится в цвет, неравный цвету текущей вершины. Если же вершина была посещена, то ребро либо пропускается, если его концы – разноцветные, а если его концы одного цвета, то делается пометка, что граф не является двудольным.

Можем осуществить поиск цикла в ориентированном графе. Цикл в ориентированном графе можно обнаружить по наличию ребра, ведущего из текущей вершины в вершину, которая в настоящий момент находится в стадии обработки, то есть алгоритм DFS зашел в такую вершину, но еще не вышел из нее. В таком алгоритме DFS будем красить вершины в три цвета. Цветом 0 («белый») будем обозначать еще непосещенные вершины. Цветом

1 («серый») будем обозначать вершины в процессе обработки, а цветом 2 («черный») будем обозначать уже обработанные вершины. Вершина красится в цвет 1 при заходе в эту вершину и в цвет 2 – при выходе. Цикл в графе существует, если алгоритм DFS обнаруживает ребро, конец которого покрашен в цвет 1.

Еще одно важное применение поиска в глубину – топологическая сортировка. Пусть дан ориентированный граф не содержащий циклов. Тогда вершины этого графа можно упорядочить так, что все ребра будут идти от вершин с меньшим номером к вершинам с большим номером. Для топологической сортировки графа достаточно запустить алгоритм DFS, при выходе из вершины добавляя вершину в конец списка с ответом. После окончания алгоритма список с ответом развернуть в противоположном порядке.

Поиск мостов. Мостом называется ребро, при удалении которого граф распадается на две компоненты связности. Алгоритм поиска в глубину позволяет найти все мосты в связном графе за один DFS, то есть за сложность O(n).

Программа, выполняющая действия над матрицами, реализована с помощью динамических массивов (так как есть необходимость задавать матрицы произвольной размерности) и функций. Использование функций в программе наглядно показано на блок – схеме.

В разобранном здесь примере совершается обход в глубину графа, представленного на рисунке ниже.

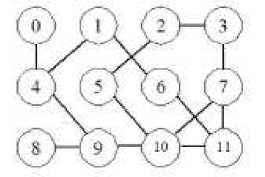
Рисунок 1 – Обход графа в глубину

Обход графа в глубину описывается следующим алгоритмом: выбрать из непройденных вершин вершину с наименьшим номером; пройти выбранную вершину и отметить её в массиве пометок как пройденную; просмотреть список инцидентности только что пройденной вершины и к каждой непройденной вершине из списка применить рекурсивно пункты 2 и 3 данного алгоритма; перейти к пункту 1.

Чтобы на экран выводился весь маршрут обхода, начиная с первой вершины, следует ввести значение переменной from (стартовая точка), на единицу меньшее номера первой вершины.

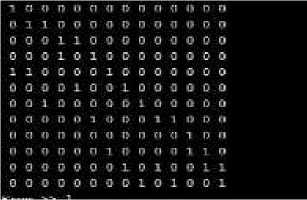
Рисунок 2 - Матрица инцидентности

10000000000000 OLLOOOOODOOOOO a о d i л Doanooooo О О О 1 0 1 0 0 D Q О 0 D 0 11000010000000 0 0 0 (I 1 0 0 1 о о о о о 0

п о i n ci о n л i n о о о о

О О О 0 0 1 О 0 0 1 1 О О 0

From » 55

)rt|wM

) 1 1 6 11 7325 10 9 В

.«Proqree finieh^d with exit ocxhs П rcw BN7EH to exit console.[]

Рисунок 3 - Последовательность вершин при вводной 55

Данный алгоритм был реализован на языке программирования C++ ,а затем проверен на наличие ошибок. Мы осуществили ручной просчет, чтобы убедится в правильности работы нашей программы. Основными структурами, при создании программы являлись: динамические массивы и циклы(while , for), а так же функции.